傅晶晶,王志亮,李松玉,封陈晨
(合肥工业大学 土木与水利工程学院,合肥 230009)
摘要:
为研究基于3D打印的层状类岩石材料动态损伤力学行为,对5组不同倾角的岩样,采用分离式霍普金森杆对其进行动态压缩试验。依据所得的应力-应变数据,以朱-王-唐本构模型为基础,建立一种线性弹簧体、Weibull分布损伤体和Maxwell体并联的黏弹性本构模型,并结合试样的残余强度特性引入损伤修正系数。最后,将其推广应用于黑色页岩的变形规律研究,以检验该本构模型的适用性。结果表明:动态冲击下岩样峰值应力随着倾角的增加呈现先减小后增大的“V”形变化趋势,与天然层状岩石的变化规律相符合；所构建的损伤本构模型,能准确地表征3D打印的层状类岩石材料的应力-应变曲线形状及其力学特征；考虑损伤修正后,其还可较好地反映试样峰后阶段应力应变变化特性与残余强度。研究结果对揭示层状岩石动载下变形规律具有一定参考价值。
关键词: 3D打印 类岩石材料 动态损伤 本构模型 残余强度
DOI：10.11918/202207119
分类号:TU45
文献标识码:A
基金项目:国家自然科学基金雅砻江联合基金 (U1965101)；国家自然科学基金(12272119)
Strength property and dynamic damage constitutive model of 3D printed rock-like material
FU Jingjing,WANG Zhiliang,LI Songyu,FENG Chenchen
(College of Civil Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract:
To investigate the dynamic damage mechanical behaviors of bedded rock-like material based on 3D printing, dynamic compression tests on five groups of printed samples with different dip angles were carried out using a split-Hopkinson pressure bar. Then, according to the obtained stress-strain data and Zhu-Wang-Tang constitutive model, a viscoelastic constitutive model was constructed by connecting the linear spring body, the Weibull distribution damage body, and the Maxwell body in parallel, and the damage correction coefficient was introduced in combination with the residual strength properties of the samples. Finally, the model was extended to explore the deformation patterns of black shale to verify its applicability. Results showed that under impact loading, the peak stress of samples displayed a "V" shaped trend with the increase in dip angle, which was consistent with the variation pattern of natural layered rock. The damage constitutive model accurately characterized the shape of the stress-strain curve and the mechanical behaviors of the 3D printed bedded rock-like material. After considering the damage correction, it also better depicted the stress-strain change characteristics and residual strength of the samples at the post-peak stage. This study is useful for understanding the deformation pattern of bedded rock subjected to dynamic loading.
Key words: 3D printing rock-like material dynamic damage constitutive model residual strength
傅晶晶, 王志亮, 李松玉, 封陈晨. 3D打印类岩石材料强度特性与动态损伤本构模型[J]. 哈尔滨工业大学学报, 2023, 55(6): 110-116. DOI: 10.11918/202207119.
FU Jingjing, WANG Zhiliang, LI Songyu, FENG Chenchen. Strength property and dynamic damage constitutive model of 3D printed rock-like material[J]. Journal of Harbin Institute of Technology, 2023, 55(6): 110-116. DOI: 10.11918/202207119.
基金项目 国家自然科学基金雅砻江联合基金(U1965101)；国家自然科学基金(12272119) 作者简介 傅晶晶(1999—)，女，硕士研究生;
王志亮(1969—)，男，博士，教授，博士生导师 通信作者 王志亮，cvewzL@hfut.edu.cn 文章历史 收稿日期: 2022-07-26
Abstract Full text Figures/Tables PDF
3D打印类岩石材料强度特性与动态损伤本构模型
傅晶晶, 王志亮
, 李松玉, 封陈晨 合肥工业大学 土木与水利工程学院，合肥 230009
收稿日期: 2022-07-26; 录用日期: 2022-10-10; 网络首发日期: 2022-11-20
基金项目: 国家自然科学基金雅砻江联合基金(U1965101)；国家自然科学基金(12272119)
作者简介: 傅晶晶(1999—)，女，硕士研究生; 王志亮(1969—)，男，博士，教授，博士生导师
通信作者: 王志亮，cvewzL@hfut.edu.cn
摘要: 为研究基于3D打印的层状类岩石材料动态损伤力学行为，对5组不同倾角的岩样，采用分离式霍普金森杆对其进行动态压缩试验。依据所得的应力-应变数据，以朱-王-唐本构模型为基础，建立一种线性弹簧体、Weibull分布损伤体和Maxwell体并联的黏弹性本构模型，并结合试样的残余强度特性引入损伤修正系数。最后，将其推广应用于黑色页岩的变形规律研究，以检验该本构模型的适用性。结果表明：动态冲击下岩样峰值应力随着倾角的增加呈现先减小后增大的“V”形变化趋势，与天然层状岩石的变化规律相符合；所构建的损伤本构模型，能准确地表征3D打印的层状类岩石材料的应力-应变曲线形状及其力学特征；考虑损伤修正后，其还可较好地反映试样峰后阶段应力应变变化特性与残余强度。研究结果对揭示层状岩石动载下变形规律具有一定参考价值。
关键词: 3D打印 类岩石材料 动态损伤 本构模型 残余强度
Strength property and dynamic damage constitutive model of 3D printed rock-like material
FU Jingjing, WANG Zhiliang
, LI Songyu, FENG Chenchen College of Civil Engineering, Hefei University of Technology, Hefei 230009, China
Abstract: To investigate the dynamic damage mechanical behaviors of bedded rock-like material based on 3D printing, dynamic compression tests on five groups of printed samples with different dip angles were carried out using a split-Hopkinson pressure bar. Then, according to the obtained stress-strain data and Zhu-Wang-Tang constitutive model, a viscoelastic constitutive model was constructed by connecting the linear spring body, the Weibull distribution damage body, and the Maxwell body in parallel, and the damage correction coefficient was introduced in combination with the residual strength properties of the samples. Finally, the model was extended to explore the deformation patterns of black shale to verify its applicability. Results showed that under impact loading, the peak stress of samples displayed a "V" shaped trend with the increase in dip angle, which was consistent with the variation pattern of natural layered rock. The damage constitutive model accurately characterized the shape of the stress-strain curve and the mechanical behaviors of the 3D printed bedded rock-like material. After considering the damage correction, it also better depicted the stress-strain change characteristics and residual strength of the samples at the post-peak stage. This study is useful for understanding the deformation pattern of bedded rock subjected to dynamic loading.
Keywords: 3D printing rock-like material dynamic damage constitutive model residual strength
3D打印是近些年迅速发展的先进成型技术，不同于传统制造技术所采用的“减材加工”等方法，以计算机生成的三维数字模型为基础，将打印材料进行逐层打印形成实体[1-2]。目前，这项技术已广泛应用于机械、医疗、工程等领域，并逐渐延展到岩土工程问题研究中。该技术结合CT扫描等细观结果，可快捷制备出含预制缺陷形态和复杂结构特征的岩体模型。由于重复性好，批次打印的岩样不但具有完全相同的结构，而且其均匀性要优于天然岩体，一定程度上解决了岩石力学试验重复性低的问题。
在过去的十年中，有学者针对这一新的研究方向进行了诸多扎实的基础工作。Jiang等[3]基于无侧限抗压强度和直接拉伸实验结果，发现以聚乳酸为打印材料和融合沉积建模的3D打印技术不适合模拟岩石。田威等[4]对3D打印岩样进行力学性能试验，并从打印岩样的单轴抗压强度和破裂状态角度分析，发现3D打印试样与天然砂岩的物理力学性质较为接近。Sharafisafa等[5]通过对含单、双裂纹的试样进行巴西圆盘准静态压缩试验，揭示了类岩石试样的预制裂纹扩展和贯通机制。蒋力帅等[6]基于砂型3D打印试样，通过开展动静态试验探析了砂型3D打印试样与天然煤样力学特性的相似性。然而，这些研究大多聚焦于静态试验下完整或含预制裂隙试样的力学特性，对含不同打印倾角的类岩石材料动态力学特性等方面的研究涉及较少。
迄今，关于天然岩石类动态本构关系的研究已经取得了瞩目成果。郭德勇等[7]根据不同冲击速度下煤岩力学响应明显的分段特征，建立含低-中-高应变率响应的黏弹性损伤本构模型。谢理想等[8]基于软岩及混凝土材料在动态压缩下的力学特点，发展了既带有损伤特性又保留了黏性单元的损伤型本构模型。Zhai等[9]为了展现岩石冻融后的动力特性，提出了一种考虑多种形式耗散能的损伤本构方程。孙清佩等[10-11]针对不同层理方向的黑色页岩，采用分离式霍普金森杆(SHPB)开展了3种应变率下动态压缩试验，并建立考虑初始损伤与受荷损伤耦合作用的本构模型。
综上，类岩石材料的动损伤特性方面虽然取得不少成果，但在其层状结构以及本构模型中考虑残余强度方面工作开展较少。为此，借鉴已有的本构模型，先采用3D打印技术重构层状大理岩试样，对其开展动态压缩试验。依据力学元件组合原理，将弹簧元件、Weibull分布损伤体与Maxwell体并联，同时考虑试样残余强度的影响，引入损伤修正系数并构建黏弹性本构模型。最后，结合室内试验结果和相关文献数据验证模型的适用性，力求得出有参考价值的结论。
1 试样及试验仪器 1.1 试样制备试样采用粉末黏结成型打印技术，设备是3D System公司生产的Project 860打印机；原材料为VisiJet PXL类石膏粉末，主要成分为CaSO4 · 0.5H2O，密度为1.4 g/cm3。在制备之前，根据CT扫描等细观试验结果，确定天然层状大理岩内部晶体结构。随后，在电脑上建立试样模型，并以STL格式导出。当打印机预热后，滚轴将供粉槽内存储的粉末推到成型槽上，每层的铺粉厚度为1 mm，打印喷头根据计算机指令在X轴和Y轴移动并将胶水喷涂至相应区域，即试样的第一层打印完毕；供粉槽向上抬高一层高度，成型槽往下降落相同的高度，滚轴再次送粉到成型槽(如图 1)，重复以上步骤即可完成试样制备[12]。打印完毕后为了使试样充分干燥，需自然晾干14 d [13]。
Fig. 1
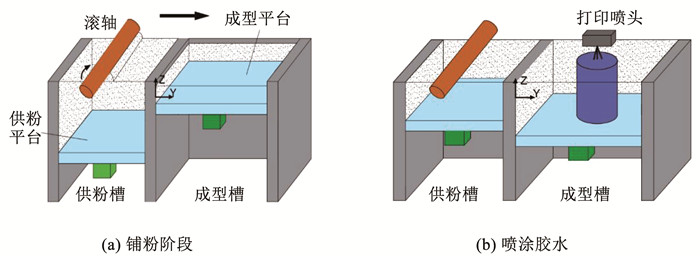图 1 3D打印工艺流程示意 Fig. 1 Schematic diagram of 3D printing process 上述用于CT扫描的大理岩试样取自锦屏二级水电站的深埋引水隧洞，其密度为2.81 g/cm3，主要成分有白云石和石英等，外观上整体呈灰白色。
在3D打印过程中，通过变化打印倾角，可制作出不同层理方向的层状试样。共设置有0°、30°、45°、60°和90°5组打印方向，每组制作不少于3个试样，尺寸为?50 mm×25 mm(如图 2所示)，两端面不平行度误差最大不超过0.05 mm。
Fig. 2
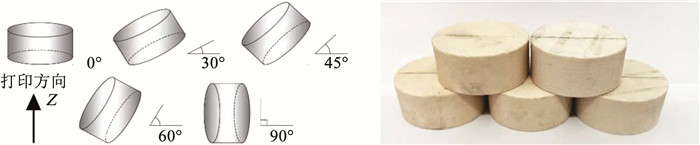图 2 3D打印试样 Fig. 2 3D printed samples 1.2 试验仪器及方法试样的冲击压缩试验在SHPB(图 3)上完成，该系统主要由驱动系统、压杆系统、信息采集及分析系统及缓冲装置组成。其中，冲击子弹的长度为0.4 m，入射杆与透射杆的长度分别为2.4和1.4 m。所有杆件都采用高强度合金钢，密度为7 900 kg/m3，弹性模量为210 GPa，试验中子弹速度均控制在7 m/s附近。
Fig. 3
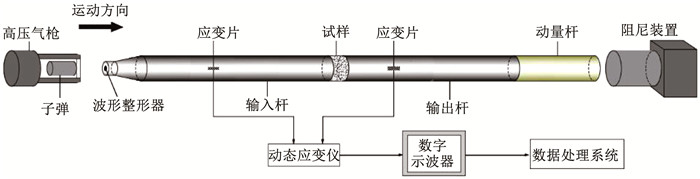图 3 SHPB试验装置 Fig. 3 Diagram of SHPB device 按照一维应力波理论，采用简化的“三波法”处理实验数据[14]，得到试样应力、应变和应变率之间的关系：
$\sigma(t)=\frac{A}{2 A_{\mathrm{S}}} E\left[\varepsilon_{\mathrm{I}}(t)+\varepsilon_{\mathrm{R}}(t)+\varepsilon_{\mathrm{T}}(t)\right]$ (1)
$\varepsilon(t)=\frac{c}{l_{\mathrm{S}}} \int_0^t\left[\varepsilon_{\mathrm{I}}(t)-\varepsilon_{\mathrm{R}}(t)-\varepsilon_{\mathrm{T}}(t)\right] \mathrm{d} t$ (2)
$\dot{\varepsilon}(t)=\frac{c}{l_{\mathrm{S}}}\left[\varepsilon_{\mathrm{I}}(t)-\varepsilon_{\mathrm{R}}(t)-\varepsilon_{\mathrm{T}}(t)\right]$ (3)
式中：A为压杆的截面积，AS为试样的截面积，c为压杆的波速，lS为试样长度，E为压杆的弹性模量，εI(t)、εR(t)、εT(t)分别为入射波、反射波、透射波的应变时程。
图 4为典型动态波形平衡图(纵轴为电压)，叠加入射波和反射波，发现其波形与透射波在峰值之前几乎重合，表明试样两端的动应力达到了平衡，即试验满足一维应力均匀性假设。在本研究中，对所有的试验结果进行了严格的应力时程检查，并剔除了少数不能满足动应力平衡的试验结果。
Fig. 4
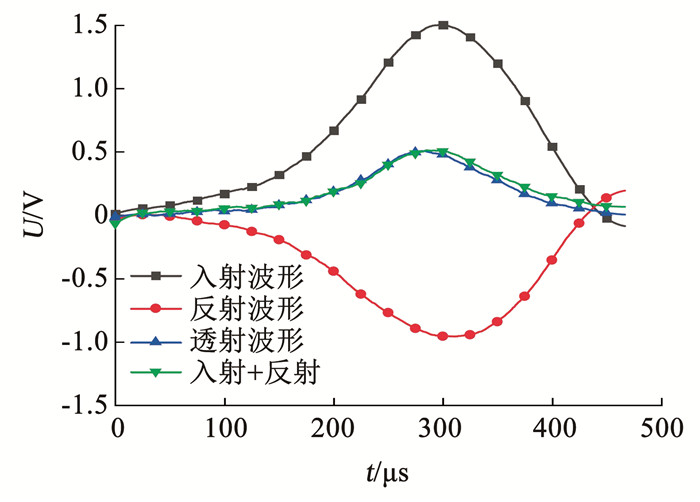图 4 压缩试验中典型的动态应力平衡 Fig. 4 Typical dynamic stress equilibrium in compression test 图 5显示的应力-应变曲线总体上可以分为两类[15]：第1类为“应变软化”型，即加载后的试样在比原来更低的应力处就能发生进一步变形，如45°和60°层理倾角时的曲线；第2类为“回弹”型，表现为当应变达到一个值后又回弹变小，峰后曲线的斜率大于0，见图 5中的0°、30°以及90°倾角的曲线。图 6为试样峰值强度与应变率变化曲线。可以看出，试样动态峰值强度随着倾角的变化呈现先减小后增大的“V”形规律，而应变率的变化规律则相反。在60°倾角时，应变率达到最大而峰值强度最小，此时各向异性显著。
Fig. 5
图 5 层状类岩石试样应力-应变曲线 Fig. 5 Stress-strain curves of bedded rock-like samples Fig. 6
图 6 峰值强度与应变率变化曲线 Fig. 6 Variation of peak strength with strain rate 2 损伤本构模型建立 2.1 ZWT本构介绍在动态冲击条件下，岩石类材料的力学特性不仅具有弹性和塑性，还展现出随时间变化的黏性。朱-王-唐(ZWT)本构模型能较好地表征这些特性，该模型是唐志平等在Green等[16]建立的高分子和金属材料的本构基础上，结合Coleman-Noll的有限线性黏弹性理论[17]，并参照试验结论推导得出的。研究发现其适用于冲击荷载下高分子复合材料、混凝土与岩石等脆性介质力学性能的表征。
图 7(a)显示该模型由两个分别描述不同应变率下黏弹性响应特征的Maxwell体和一个理想弹簧元件并联组成，低频和高频部分的松弛时间φ1、φ2量级范围一般对应为10~102和10-4~10-6 s；E1、E2表示不同Maxwell体中弹簧的弹性模量；η1与η2代表不同响应下黏壶的黏滞系数。具体本构方程为
$\begin{aligned}\sigma= & f(\varepsilon)+E_1 \int_0^t \dot{\varepsilon} \exp \left(-\frac{t-\tau}{\eta_1}\right) \mathrm{d} \tau+ \\& E_2 \int_0^t \dot{\varepsilon} \exp \left(-\frac{t-\tau}{\eta_2}\right) \mathrm{d} \tau\end{aligned}$ (4)
$f(\varepsilon)=E_0 \varepsilon+\lambda \varepsilon^2+\gamma \varepsilon^3$ (5)
Fig. 7
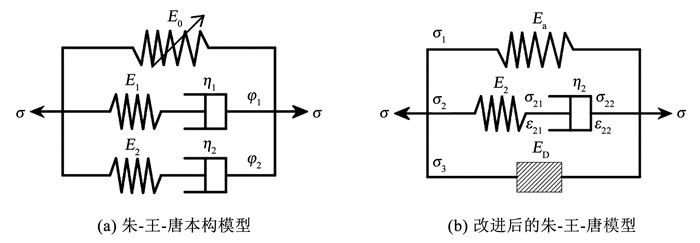图 7 本构模型示意 Fig. 7 Schematic diagram of constitutive model 2.2 考虑残余强度的修正模型ZWT模型对于类岩石材料的应用略显复杂，在构建3D打印大理岩的本构模型时，需综合考虑初始损伤和应变率硬化等效应对材料动态力学特性的影响，故对模型进行以下改进：
1) 式(5)中f(ε)多项式描述材料的弹性性能与应变率无关。此外，f(ε)中后两项是平衡应力泰勒展开式的近似项，由于应变的量级很小，可省略后两项直接简化成线性弹簧元件。
2) 上述1.2节冲击试验结果表明，当应变率量级为102，应变量级为10-3~10-2，此过程中低频Maxwell体无足够的时间进行应力松弛，可将其视作一个普通的弹簧元件。
3) ZWT模型虽然能够反映材料的黏弹性特征以及在冲击荷载下的力学响应，却忽视了材料的损伤特性，而对于层状3D打印试样，损伤是不可忽略的。所以，并联一个反映损伤演化特性损伤体D。
改进后的本构模型见图 7(b)所示，其应力-应变关系为
$\sigma(t)=\sigma_1(t)+\sigma_2(t)+\sigma_3(t)$ (6)
其中，弹簧体的本构关系表达如下：
$\sigma_1(t)=E_{\mathrm{a}} \varepsilon$ (7)
式中Ea=E0+E1。
对于串联弹簧元件和黏滞体得到的Maxwell体，有
$\sigma_2(t)=\sigma_{21}(t)=\sigma_{22}(t)$ (8)
$\varepsilon_2(t)=\varepsilon_{21}(t)+\varepsilon_{22}(t)$ (9)
$\sigma_{21}(t)=E_2 \varepsilon_{21}(t)$ (10)
$\sigma_{22}(t)=\eta_2 \dot{\varepsilon}_{22}(t)$ (11)
对式(9)两边求导，并联合式(8)、(10)和(11)得
$\dot{\varepsilon}_2(t)=\frac{\dot{\sigma}_2(t)}{E_2}+\frac{\sigma_2(t)}{\eta_2}$ (12)
对式(12)进行拉普拉斯变化后可得
$L\left[\dot{\varepsilon}_2(t)\right]=L\left[\frac{\dot{\sigma}_2(t)}{E_2}\right]+L\left[\frac{\sigma_2(t)}{\eta_2}\right]$ (13)
$\frac{\dot{\varepsilon}_2}{S}=\frac{S \varepsilon_2(S)-\sigma_2(0)}{E_2}+\frac{\sigma_2(S)}{\eta_2}$ (14)
其中S为拉普拉斯复函数。
将边界条件σ(0)=0代入式(14)整理得
$\sigma_2(S)=\eta_2 \dot{\varepsilon}_2\left(\frac{1}{S}-\frac{1}{S+E_2 / \eta_2}\right)$ (15)
对式(15)进行拉普拉斯逆变换得
$L^{-1}\left[\sigma_2(S)\right]=\eta_2 \dot{\varepsilon}_2 L^{-1}\left(\frac{1}{S}-\frac{1}{S+E_2 / \eta_2}\right)$ (16)
$\sigma_2(t)=\eta_2 \dot{\varepsilon}_2\left[1-\exp \left(-\frac{E_2}{\eta_2} \frac{\varepsilon_2}{\dot{\varepsilon}_2}\right)\right]$ (17)
假设岩体是由大量微元体构成的集合，可以将微元视为一个质点。在微元体强度服从Weibull分布前提下，损伤变量D可表达如下[18-19]：
$D=1-\exp \left[-\frac{1}{m}\left(\frac{\varepsilon}{\varepsilon_{\max }}\right)^m\right]$ (18)
式中D的取值范围为0~1.0。
考虑到岩样的残余强度特性，引入损伤修正系数ξ(0 < ξ < 1)。根据Lemaitre应变等效原理[20]，修正后的损伤体表达式为
$\left\{\sigma_3\right\}=[\boldsymbol{C}]\left\{\varepsilon_3\right\} /(1-\xi D)$ (19)
$\xi=\sqrt{\frac{\sigma_{\mathrm{r}}}{\sigma_{\mathrm{c}}}}$ (20)
式中：σ3为有效应力，[C]为材料弹性矩阵，σr为残余强度，σc为峰值强度。
将式(18)代入式(19)可得
$\begin{aligned}\sigma_3(t)= & (1-\xi D) E_3 \varepsilon(t)= \\& \left\{1-\xi+\xi \exp \left[-\frac{1}{m}\left(\frac{\varepsilon}{\varepsilon_{\max }}\right)^m\right]\right\} E_3 \varepsilon\end{aligned}$ (21)
基于损伤修正的动态本构方程表示为
$\begin{array}{r}\sigma=E_{\mathrm{a}} \varepsilon+\eta_2 \dot{\varepsilon}\left[1-\exp \left(-\frac{E_2}{\eta_2} \frac{\varepsilon}{\dot{\varepsilon}}\right)\right]+ \\\left\{1-\xi+\xi \exp \left[-\frac{1}{m}\left(\frac{\varepsilon}{\varepsilon_{\max }}\right)^m\right]\right\} E_3 \varepsilon\end{array}$ (22)
3 模型验证 3.1 模型参数确定及其验证该本构模型涉及Ea、E2、E3、η2、m和ξ 6个参数。其中，损伤修正系数ξ可由式(20)计算得出，结果见表 1。黏滞系数η2在0.1~0.5取值。余下4个模型参数，先利用试样准静态和准动态的压缩曲线拟合得到Ea、E2，然后拟合高应变率冲击下试样的力学关系曲线，得到E3和η2，各参数取值见表 2。
表 1
表 1 3D打印岩样的损伤本构参数 Tab. 1 Damage constitutive parameters of 3D printed rock samples 层理倾角θ/(°) σc/MPa σr/MPa εmax ξ 0 32.479 17.783 0.015 02 0.718
30 30.620 15.910 0.013 57 0.721
45 25.294 8.208 0.010 78 0.570
60 23.993 1.309 0.009 88 0.234
90 37.891 12.756 0.011 01 0.580
表 1 3D打印岩样的损伤本构参数 Tab. 1 Damage constitutive parameters of 3D printed rock samples
表 2
表 2 3D打印类岩石材料模型参数 Tab. 2 Model parameters of 3D printed rock-like material 层理倾角θ/(°) 应变率/s-1 Ea/GPa η2 E2/GPa E3/GPa m 0 48.39 2.128 0.3 0.269 0.835 4.428
30 64.46 1.256 0.3 0.160 0.907 8.524
45 95.35 0.783 0.3 0.135 0.232 5.119
60 109.24 0.835 0.3 0.280 0.745 3.422
90 73.92 0.968 0.3 0.123 0.524 7.728
表 2 3D打印类岩石材料模型参数 Tab. 2 Model parameters of 3D printed rock-like material
图 8给出了模型理论拟合曲线与试验数据对比。可以看出，在倾角为45°时，修正后曲线的峰值应变较未修正的曲线更接近试验值；在倾角为60°时，就其峰后阶段，修正后的理论曲线吻合度较高，与试验值相比理论曲线误差较小；当倾角为0°、30°和90°时，拟合曲线在峰前阶段与试验曲线几乎重合，但由于本构模型中应力与应变一一对应，难以表征出“回弹型”全应力-应变关系。整体而言，修正后的本构模型可较好地表征基于3D打印的层状类岩石材料力学特性。
Fig. 8
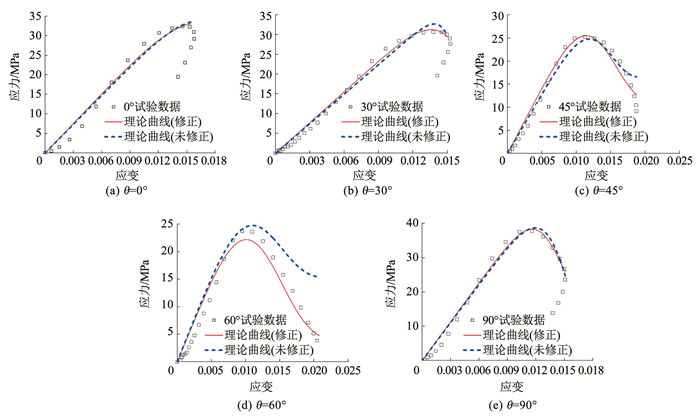图 8 理论拟合曲线与试验数据对比 Fig. 8 Comparison of theoretical fitting results with test data 3.2 模型适用性检验为了进一步考察上述本构模型的适用性，特引用黑色层状页岩单轴冲击压缩试验结果[10]进行验证。表 3和图 9显示，当应变率为102.35 s-1，本文模型比孙清佩等提出的模型[10](以下简称“孙模型”)拟合优度或可决系数要高，特别是层理倾角为15°时，可决系数远高于孙模型，对可决系数稍低的90°曲线也能达到0.991。当应变率为147.27 s-1时，本文模型拟合的峰值强度和峰值应变与实测数据非常吻合，如图 9(b)、(d)和(f)所示。此外，由于本文模型考虑了峰后阶段残余强度的修正，拟合曲线对黑色层理页岩峰后阶段的应力-应变关系也能很好地表征(见图 9(a)、(b)和(f))；当应变率为190.77 s-1时，本文模型不但准确地描述了峰前阶段的应力变化规律(见图 9(d))，而且对曲线峰后阶段特征也能准确地揭示(见图 9(b)、(e)和(f))。
表 3
表 3 曲线拟合的可决系数 Tab. 3 Coefficients of determination of curve fitting 应变率/s-1 θ=0° θ=15° θ=30° θ=45° θ=75° θ=90° 文献[10] 本文 文献[10] 本文 文献[10] 本文 文献[10] 本文 文献[10] 本文 文献[10] 本文
102.35 0.885 0.890 0.831 0.912 0.864 0.873 0.980 0.992 0.989 0.990 0.999 0.991
147.27 0.985 0.994 0.998 0.991 0.995 0.997 0.958 0.980 0.993 0.993 0.975 0.994
190.77 0.991 0.990 0.978 0.992 0.999 0.992 0.994 0.992 0.996 0.991 0.980 0.998
表 3 曲线拟合的可决系数 Tab. 3 Coefficients of determination of curve fitting
Fig. 9
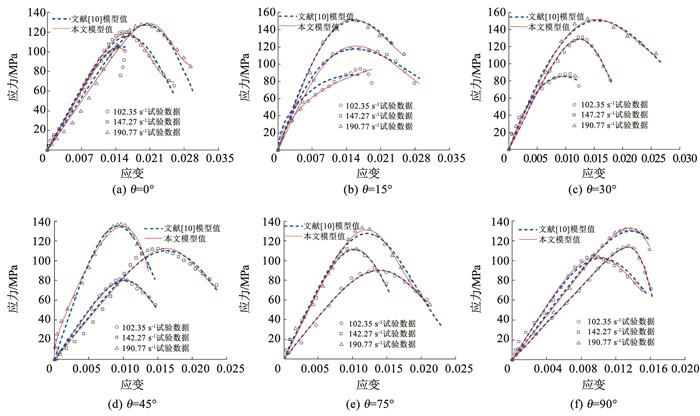图 9 黑色页岩试样应力-应变曲线对比 Fig. 9 Comparison of stress-strain curves of black shale samples 4 结论结合基于3D打印的层状类岩石试样动态测试数据，对传统的朱-王-唐本构模型进行改进，在考虑试样残余强度的基础上引入损伤修正系数，并通过试验结果和文献数据对模型进行了验证，主要结论如下：
1) 基于3D打印的层状类岩石材料单轴动态压缩应力-应变曲线有“回弹”和“应变软化”两种类型；其动态抗压强度随倾角的变化呈现先减小后增大的“V”形变化趋势，应变率则相反，在60°倾角时试样各向异性显著。
2) 所发展的动态损伤本构模型能较好地反映基于3D打印的层状类岩石试样动态压缩下应力-应变行为，修正前后的曲线在峰前阶段差异不甚明显，但引入了损伤修正系数的理论模型曲线能准确地揭示出试样峰后阶段的变化规律。
3) 所发展的动态损伤本构模型具有较强的适用性，不但可对3D打印类岩石材料和真实的页岩适用良好，而且能对低应变率下回弹型应力-应变曲线的峰前阶段特性以及中高应变率下应变软化行为等均能进行很好的表征。
参考文献
[1] CHUA C K, LEONG K F, LIM C S. Rapid prototyping: principles and applications[M]. 2nd ed. Hackensack: World Scientific Publishing Co, Inc, 2003.
[2] MOON S K, TAN Y E, HWANG J, et al. Application of 3D printing technology for designing light-weight unmanned aerial vehicle wing structures[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2014, 1(3): 223. DOI:10.1007/s40684-014-0028-x
[3] JIANG Chao, ZHAO Gaofeng. A preliminary study of 3D printing on rock mechanics[J]. Rock Mechanics and Rock Engineering, 2015, 48(3): 1041. DOI:10.1007/s00603-014-0612-y
[4] 田威, 裴志茹, 韩女. 基于CT扫描与3D打印技术的岩体三维重构及力学特性初探[J]. 岩土力学, 2017, 38(8): 2297.
TIAN Wei, PEI Zhiru, HAN Nü. A preliminary research on three-dimensional reconstruction and mechanical characteristics of rock mass based on CT scanning and 3D printing technology[J]. Rock and Soil Mechanics, 2017, 38(8): 2297. DOI:10.16285/j.rsm.2017.08.018
[5] SHARAFISAFA M, SHEN Luming, XU Qingfeng. Characterisation of mechanical behaviour of 3D printed rock-like material with digital image correlation[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 112: 122. DOI:10.1016/j.ijrmms.2018.10.012
[6] 蒋力帅, 吴星宇, 王庆伟, 等. 砂型3D打印类煤试样动静组合加载力学特性[J]. 煤炭学报, 2022, 47(3): 1196.
JIANG Lishuai, WU Xingyu, WANG Qingwei, et al. Study on dynamic mechanical behaviors of sand-powder 3D printing rock-like specimens under coupled static and dynamic loads[J]. Journal of Coal Science & Technology, 2022, 47(3): 1196. DOI:10.13225/j.cnki.jccs.xr21.1529
[7] 郭德勇, 吕鹏飞, 赵杰超, 等. 煤岩冲击变形破坏特性及其本构模型[J]. 煤炭学报, 2018, 43(8): 2233.
GUO Deyong, Lü Pengfei, ZHAO Jiechao, et al. Deformation and damage characteristics and constitutive model of coal and rock under impact loading[J]. Journal of Coal Science & Technology, 2018, 43(8): 2233. DOI:10.13225/j.cnki.jccs.2018.0300
[8] 谢理想, 赵光明, 孟祥瑞. 软岩及混凝土材料损伤型黏弹性动态本构模型研究[J]. 岩石力学与工程学报, 2013, 32(4): 857.
XIE Lixiang, ZHAO Guangming, MENG Xiangrui. Research on damage viscoelastic dynamic constitutive model of soft rock and concrete materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 857. DOI:10.3969/j.issn.1000-6915.2013.04.027
[9] ZHAI Yue, MENG Fandong, LI Yubai, et al. Research on dynamic compression failure characteristics and damage constitutive model of sandstone after freeze-thaw cycles[J]. Engineering Failure Analysis, 2022, 140: 1350. DOI:10.1016/j.engfailanal.2022.106577
[10] 孙清佩, 张志镇, 李培超, 等. 黑色页岩动载破坏的层理效应及损伤本构模型研究[J]. 岩石力学与工程学报, 2019, 38(7): 1319.
SUN Qingpei, ZHANG Zhizhen, LI Peichao, et al. Study on the bedding effect and damage constitutive model of black shale under dynamic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(7): 1319. DOI:10.13722/j.cnki.jrme.2018.1333
[11] 华敏杰. 3D打印技术在岩石力学试样制备方面的应用探讨[D]. 南京: 南京大学, 2015
HUA Minjie. Preliminary study on the application of 3D printing technology in specimen preparation of rock mechanics[D]. Nanjing: Nanjing University, 2015
[12] 张迪湦, 杨建明, 黄大志, 等. 3DP法三维打印技术的发展与研究现状[J]. 制造技术与机床, 2017(3): 38.
ZHANG Disheng, YANG Jianming, HUANG Dazhi, et al. Development and research status of three dimensional printing technology with 3DP[J]. Manufacturing Technology & Machine Tool, 2017(3): 38. DOI:10.19287/j.cnki.1005-2402.2017.03.004
[13] 刘泉声, 何璠, 邓鹏海, 等. 3D打印技术在岩石物理力学试验中的应用[J]. 岩土力学, 2019, 40(9): 3397.
LIU Quansheng, HE Fan, DENG Penghai, et al. Application of 3D printing technology to physical modeling in rock mechanics[J]. Rock and Soil Mechanics, 2019, 40(9): 3397. DOI:10.16285/j.rsm.2018.0991
[14] WAWERSIK W R, FAIRHURST C. A study of brittle rock fracture in laboratory compression experiments[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1970, 7(4): 561. DOI:10.1016/0148-9062(70)90007-0
[15] ZHOU Yingxin, XIA Kaiwen, LI Xibing, et al. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 49: 105. DOI:10.1016/j.ijrmms.2011.10.004
[16] GREEN A E, RIVLI R S. The mechanics of non-linear materials with memory[J]. Archive for Rational Mechanics and Analysis, 1957, 1: 1. DOI:10.1007/BF00297992
[17] COLEMAN B D, NOLL W. An approximation theorem for functionals with applications in continuum mechanics[J]. Archive for Rational Mechanics and Analysis, 1960, 6: 355. DOI:10.1007/BF00276168
[18] 王登科, 刘淑敏, 魏建平, 等. 冲击破坏条件下煤的强度型统计损伤本构模型与分析[J]. 煤炭学报, 2016, 41(12): 3024.
WANG Dengke, LIU Shumin, WEI Jianping, et al. Analysis and strength statistical damage constitutive model of coal under impacting failure[J]. Journal of China Coal Society, 2016, 41(12): 3024. DOI:10.13225/j.cnki.jccs.2016.0540
[19] 吴政, 张承娟. 单向荷载作用下岩石损伤模型及其力学特性研究[J]. 岩石力学与工程学报, 1996, 15(1): 55.
WU Zheng, ZHANG Chengjuan. Investigation of rock damage model and its mechanical behaviour[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1): 55.
[20] XU Xiaoli, KARAKUS M, GAO Feng, et al. Thermal damage constitutive model for rock considering damage threshold and residual strength[J]. Journal of Central South University, 2018, 25(10): 2523. DOI:10.1007/s11771-018-3933-2
