周喻1,邹世卓1,高永涛1,郭万红1,2,3,吴晓灵1
(1.金属矿山高效开采与安全教育部重点实验室(北京科技大学),北京 100083; 2.中国水电基础局有限公司,天津 301700;3.中国电建路桥集团有限公司,北京 100048)
摘要:
为研究冲击载荷作用下层状复合岩体的动态力学性能和破裂机制,基于煤单体和白砂岩构成层状软硬煤岩复合体,利用分离式霍普金森压杆试验装置和LS-DYNA有限元分析软件,结合Holmquist-Johnson-Cook(HJC)本构模型,开展不同速率和不同冲击方向下层状软硬煤岩复合体加载试验。结果表明:静态载荷作用下,层状煤岩复合体的强度不会随加载方向变化,动态载荷下层状煤岩复合体的峰值应力和动态增长因子DIF都随冲击速度增加呈线性增大,并且波阻抗匹配效果更好的HS复合体力学性能始终优于SH复合体(S和H分别代表煤单体和白砂岩),随着冲击速度增加这种现象逐渐减弱；层状煤岩复合体耗散能密度与入射能密度呈二次增长关系,分形维数也随着速度增加而不断增大,其中,应力波由硬入软时得到的效果优于由软入硬；层状煤岩复合体破碎程度随冲击速度增加而愈发剧烈,HS复合体破坏程度大于同条件下的SH复合体,白砂岩多呈剪切状破碎,煤单体多呈粉碎锥形破坏；层状煤岩复合体交界处与其他区域强度不一致,造成复合体破坏顺序改变,复合体整体强度规律从小到大依次为煤单体非交界面区域、煤单体交界面区域、白砂岩交界面区域、白砂岩非交界面区域。
关键词: 层状复合体 分离式霍普金森压杆 波阻抗 LS-DYNA Holmquist-Johnson-Cook 分形理论 能量耗散
DOI：10.11918/202207020
分类号:TD315
文献标识码:A
基金项目:中央高校基本科研业务费专项资金(FRF-IDRY-GD22-005)；国家自然科学基金青年基金(51504016)
Test and numerical simulation for mechanical properties of laminated rock mass under dynamic loading
ZHOU Yu1,ZOU Shizhuo1,GAO Yongtao1,GUO Wanhong1,2,3,WU Xiaoling1
(1.Key Laboratory for Efficient Mining and Safety of Metal Mine (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China; 2.Sinohydro Foundation Engineering Co., Ltd., Tianjin 301700, China; 3.PowerChina Road Bridge Group Co., Ltd., Beijing 100048, China)
Abstract:
To study the dynamic mechanical properties and rupture mechanism of laminated composite rock mass under the action of impact loading, we carried out loading tests of laminated soft and hard coal rock composites consisting of coal monomer and white sandstone under different rates and impact directions by using the split Hopkinson pressure bar (SHPB) device and LS-DYNA finite element analysis software combined with Holmquist-Johnson-Cook (HJC) constitutive model. Results show that the strength of the laminated coal-rock composite did not change with the loading direction under static loading. The peak stress and dynamic increase factor (DIF) of the laminated coal-rock composite under dynamic loading increased linearly with the impact velocity. The mechanical properties of HS (H and S represent white sandstone and coal monomer respectively) composite with better wave impedance matching were always better than those of SH composite, and this phenomenon gradually decreased with the increase in the impact velocity. The dissipation energy density and incident energy density of the laminated coal-rock composite showed a quadratic growth relationship. The fractal dimension increased with the velocity, and the effect obtained when the stress wave transferred from hard into soft was better than that from soft into hard. The degree of fragmentation of the laminated coal-rock composite became more and more intense with the increase in the impact velocity, the degree of destruction of HS composite was greater than that of SH composite under the same conditions, the white sandstone presented more shear-like fragmentation, and the coal monomer presented more crushed conical destruction. The strength at the interface of the laminated coal-rock composite was not consistent with that in other regions, resulting in a change in the order of destruction of the composite. The overall strength law of the composite from small to large was: coal monomer non-interface region, coal monomer interface region, white sandstone interface region, and white sandstone non-interface region.
Key words: laminated composite split Hopkinson pressure bar wave impedance LS-DYNA Holmquist-Johnson-Cook fractal theory energy dissipation
周喻, 邹世卓, 高永涛, 郭万红, 吴晓灵. 动载下层状岩体力学特性试验与数值模拟[J]. 哈尔滨工业大学学报, 2023, 55(6): 93-109. DOI: 10.11918/202207020.
ZHOU Yu, ZOU Shizhuo, GAO Yongtao, GUO Wanhong, WU Xiaoling. Test and numerical simulation for mechanical properties of laminated rock mass under dynamic loading[J]. Journal of Harbin Institute of Technology, 2023, 55(6): 93-109. DOI: 10.11918/202207020.
基金项目 中央高校基本科研业务费专项资金(FRF-IDRY-GD22-005)；国家自然科学基金青年基金(51504016) 作者简介 周喻(1985—)，男，博士，副教授 通信作者 邹世卓，2267725130@qq.com 文章历史 收稿日期: 2022-07-06
Abstract Full text Figures/Tables PDF
动载下层状岩体力学特性试验与数值模拟
周喻1, 邹世卓1
, 高永涛1, 郭万红1,2,3, 吴晓灵1 1. 金属矿山高效开采与安全教育部重点实验室(北京科技大学)，北京 100083;
2. 中国水电基础局有限公司，天津 301700;
3. 中国电建路桥集团有限公司，北京 100048
收稿日期: 2022-07-06; 录用日期: 2022-09-05; 网络首发日期: 2022-10-10
基金项目: 中央高校基本科研业务费专项资金(FRF-IDRY-GD22-005)；国家自然科学基金青年基金(51504016)
作者简介: 周喻(1985—)，男，博士，副教授
通信作者: 邹世卓，2267725130@qq.com
摘要: 为研究冲击载荷作用下层状复合岩体的动态力学性能和破裂机制，基于煤单体和白砂岩构成层状软硬煤岩复合体，利用分离式霍普金森压杆试验装置和LS-DYNA有限元分析软件，结合Holmquist-Johnson-Cook(HJC)本构模型，开展不同速率和不同冲击方向下层状软硬煤岩复合体加载试验。结果表明：静态载荷作用下，层状煤岩复合体的强度不会随加载方向变化，动态载荷下层状煤岩复合体的峰值应力和动态增长因子DIF都随冲击速度增加呈线性增大，并且波阻抗匹配效果更好的HS复合体力学性能始终优于SH复合体(S和H分别代表煤单体和白砂岩)，随着冲击速度增加这种现象逐渐减弱；层状煤岩复合体耗散能密度与入射能密度呈二次增长关系，分形维数也随着速度增加而不断增大，其中，应力波由硬入软时得到的效果优于由软入硬；层状煤岩复合体破碎程度随冲击速度增加而愈发剧烈，HS复合体破坏程度大于同条件下的SH复合体，白砂岩多呈剪切状破碎，煤单体多呈粉碎锥形破坏；层状煤岩复合体交界处与其他区域强度不一致，造成复合体破坏顺序改变，复合体整体强度规律从小到大依次为煤单体非交界面区域、煤单体交界面区域、白砂岩交界面区域、白砂岩非交界面区域。
关键词: 层状复合体 分离式霍普金森压杆 波阻抗 LS-DYNA Holmquist-Johnson-Cook 分形理论 能量耗散
Test and numerical simulation for mechanical properties of laminated rock mass under dynamic loading
ZHOU Yu1, ZOU Shizhuo1
, GAO Yongtao1, GUO Wanhong1,2,3, WU Xiaoling1 1. Key Laboratory for Efficient Mining and Safety of Metal Mine (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China;
2. Sinohydro Foundation Engineering Co., Ltd., Tianjin 301700, China;
3. PowerChina Road Bridge Group Co., Ltd., Beijing 100048, China
Abstract: To study the dynamic mechanical properties and rupture mechanism of laminated composite rock mass under the action of impact loading, we carried out loading tests of laminated soft and hard coal rock composites consisting of coal monomer and white sandstone under different rates and impact directions by using the split Hopkinson pressure bar (SHPB) device and LS-DYNA finite element analysis software combined with Holmquist-Johnson-Cook (HJC) constitutive model. Results show that the strength of the laminated coal-rock composite did not change with the loading direction under static loading. The peak stress and dynamic increase factor (DIF) of the laminated coal-rock composite under dynamic loading increased linearly with the impact velocity. The mechanical properties of HS (H and S represent white sandstone and coal monomer respectively) composite with better wave impedance matching were always better than those of SH composite, and this phenomenon gradually decreased with the increase in the impact velocity. The dissipation energy density and incident energy density of the laminated coal-rock composite showed a quadratic growth relationship. The fractal dimension increased with the velocity, and the effect obtained when the stress wave transferred from hard into soft was better than that from soft into hard. The degree of fragmentation of the laminated coal-rock composite became more and more intense with the increase in the impact velocity, the degree of destruction of HS composite was greater than that of SH composite under the same conditions, the white sandstone presented more shear-like fragmentation, and the coal monomer presented more crushed conical destruction. The strength at the interface of the laminated coal-rock composite was not consistent with that in other regions, resulting in a change in the order of destruction of the composite. The overall strength law of the composite from small to large was: coal monomer non-interface region, coal monomer interface region, white sandstone interface region, and white sandstone non-interface region.
Keywords: laminated composite split Hopkinson pressure bar wave impedance LS-DYNA Holmquist-Johnson-Cook fractal theory energy dissipation
近年来，随着人类社会发展的逐步进行，地下开采不断向着深部探索。超深地质环境下的复杂应力条件使岩体力学性能改变，层状复合体作为典型地下岩体，研究其动态力学性能和破碎规律对凿岩掘进、矿山开拓、隧道开采和爆破等具有重大参考意义[1-3]。目前，有关层状岩体静力学的研究已经十分完善，腾俊洋等[4-6]借助单轴岩石压力机，开展了结构面倾角和组合方式变化时，层状岩体的静力学强度特征和损伤演化规律研究。结果表明，在不同结构面倾角和组合方式下，层状岩体的力学特性和破坏规律都会随之变化。针对结构面对层状岩体的作用机制，王旭一等[7]基于Weibull分布的接触模型，提出了层状岩体的力学模型理论，并通过单轴压缩试验进行了验证；邓华锋等[8]根据不同节理倾角层状岩体的纵波波速和单轴压缩试验结果，建立了层状岩体的力学参数计算方法；刘自由等[9-10]分别依据三轴压力机和FLAC有限差分软件研究了界面效应的影响。可以发现，结构面是影响层状岩体力学性能和各向异性的重要控制因素，相关研究也可以为岩体质量评价指标提供参考意义。此外，陈宇龙等[11-14]通过数值模拟软件研究了层状岩体在单轴和三轴压缩情况下的力学性能演化。针对层状岩体的静力学研究可以为巷道、采矿区、隧道等工程强度设计与稳定性分析提供理论依据，但事实上，动态载荷冲击能更好地模拟现场实际情况，比如爆破、放矿、凿岩等情况下，尖点突变应力会改变原有的静态本构模型，从而增加未知风险发生的可能性。
现有的层状岩体动力学特性研究多基于分离式霍普金森压杆试验装置(split Hopkinson pressure bar, SHPB)完成，霍普金森压杆试验装置可以调节应变率以满足不同的实验需要，在岩爆预测、岩石特性探究、应力扰动研究、动力冲击模拟等方面优势显著，由于其操作简单、结果准确、可重复性高，现已成为一种被普遍认可的研究方法。刘运思等[15-18]借助SHPB试验装置，针对不同层理面倾角和加载速率对层状岩体动力学性能的影响机制展开研究。结果表明，不同层理面倾角下复合岩体的破坏模式会受到显著影响，并且随着加载速率的增大，这种现象会变得愈发显著。Xie等[19]使用霍普金森压杆实验装置对4种不同比例的复合煤岩进行冲击，研究不同煤砂比下的主要破坏形式和动态力学性能变化，并使用LS-DYNA进行了验证。此外，杜超超等[20]利用一维动静组合加载装置，研究了不同冲击气压下，轴压以及岩层倾角对复合岩石材料动态力学性能和破坏模式的影响，李成杰等[21-22]对预置裂隙类煤岩组合体也开展了此类研究，探讨了裂隙位置与倾角的影响机制。在上述针对层状岩体动力学特性的研究中，与静力学研究类似，多以结构面为切入点展开分析，事实上层状岩体的冲击方向也会对力学特性产生显著影响，例如，杨仁树等[23]基于波阻抗理论研究了压杆与试样匹配效应不同时的复合岩体力学性能，此类研究对于炸药爆破、巷道掘进等具有理论指导意义。
目前，学者们基于理论分析、室内试验和数值模拟等方法，针对层状复合体的静力学和动力学性能开展了一系列研究，但冲击方向的不同对层状复合体动态力学性能和破坏机制的影响鲜有报道。本试验基于分离式霍普金森压杆试验装置(SHPB)对层状复合体进行不同冲击方向和冲击速度的加载试验，研究其动态力学性能变化、能量耗散规律、宏观破坏特征和细观损伤机制。同时结合LS-DYNA有限元分析软件，基于Holmquist-Johnson-Cook(HJC)本构模型揭示层状复合体动态破坏过程。研究结果可以为层状复合体破碎动力学和实际工程应用提供理论指导。
1 试验 1.1 层状岩体制备在煤矿中，砂岩常常赋存在煤层的顶板或底板，因此，选取煤单体和白砂岩组成典型层状岩体。白砂岩作为硬岩的代表，与软弱岩煤单体的复合可表征绝大多数层状岩体的力学特性。两种岩石取自河南新乡的某矿场，为保证实验样品的一致性，在地质调研后，选取一块较大的完整岩样进行一次性钻孔加工。岩样加工过程中严格按照ISRM建议标准[24]，断面不平行度和不垂直度在±0.02 mm以内，并利用波速测量仪剔除波速差异过大的样品。分别加工和切割两种岩石，各得到20个?50 mm×25 mm圆盘和2个?50 mm×100 mm标准样。在原岩应力与地下水的作用下，层状岩体往往以黏合状态赋存，区别于简单叠加，其应力波传递和破碎规律都会发生变化，因此，需要将两种岩石黏合，以表征真实的地下层状岩体。已有文献表明，环氧树脂作为黏合剂可以较好地模拟黏结情况下的岩石力学行为[25]。因此，在控制环氧树脂用量的前提下，对两种岩体进行黏合，得到如图 1所示试样。根据试样接受应力波冲击的方向，将试样分为软-硬复合岩体和硬-软复合岩体，分别记作S-H和H-S。
Fig. 1
图 1 层状复合体试样实物照片 Fig. 1 Physical images of laminated composite samples 为了充分理解白砂岩组分和煤单体组分内部结构的差异，对层状岩体进行三维CT扫描，试验仪器采用中国天津三英公司生产的NanoVoxel-3502E高分辨X射线三维断层扫描成像系统，扫描电压160 kV、电流45 μA、分辨率37.79 μm，扫描方式为CT螺旋扫描，扫描帧数为1 440帧/圈、曝光时间为0.3 μs、图像合并数为2。试样微观结构扫描如图 2所示。可以看出，白砂岩质地紧密坚硬，不含其他成分，而煤单体内部裂隙发达，并含有较多杂质。环氧树脂使两种质地不同的岩石紧密连接，构成典型的软-硬岩复合体。
Fig. 2
图 2 层状复合体内部结构CT扫描 Fig. 2 CT scanning of internal structure of laminated composites 1.2 试验方案由Xie等[19]的研究可知，层状岩体在动态载荷和静态载荷的作用下，破坏机制会有一定差别。本试验采用分离式霍普金森压杆试验装置(SHPB)完成对复合岩体的动态冲击试验，借助YAW-600微机控制电液伺服岩石压力试验机完成对复合岩体的静力学加载试验。
分离式霍普金森压杆试验装置(SHPB)如图 3所示，压杆直径为50 mm，子弹为纺锤形，冲击波波形为正弦波，入射杆和透射杆为2.5 m，材质为合金钢，密度为7.8×103 kg/m3，弹性模量为240 GPa，纵波波速为5 200 m/s。
Fig. 3
图 3 SHPB试验测试系统 Fig. 3 SHPB test system 如图 4所示，应力波通过入射杆传递至试样，试样与压杆之间涂抹黄油以减少摩擦效应[26]。在实验中为了防止压杆挤压力造成的预置围压对实验结果产生影响，应使试样缓慢划入压杆之间，靠黄油间的液体张力自行固定。由于在操作中速度的控制是由纺锤形弹头的位置与冲击气压的大小共同控制，可能会造成与预先设定速度的偏差。
Fig. 4
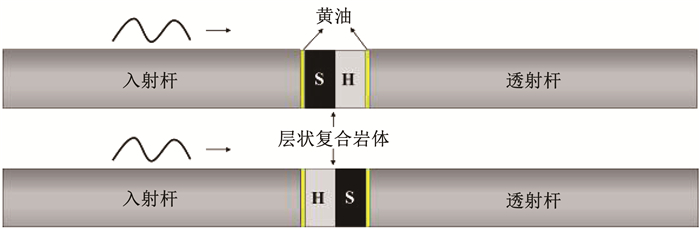图 4 SHPB冲击过程示意 Fig. 4 Schematic of SHPB impact process 实验采用传统的三波法进行数据处理，即
$\sigma(t)=\frac{A_{\mathrm{e}} E_{\mathrm{e}}}{2 A_{\mathrm{s}}}\left[\varepsilon_{\mathrm{I}}(t)+\varepsilon_{\mathrm{R}}(t)+\varepsilon_{\mathrm{T}}(t)\right]$ (1)
$\varepsilon(t)=\frac{C_{\mathrm{e}}}{L_{\mathrm{s}}} \int_0^t\left[\varepsilon_{\mathrm{I}}(t)-\varepsilon_{\mathrm{R}}(t)-\varepsilon_{\mathrm{T}}(t)\right] \mathrm{d} t$ (2)
$\dot{\varepsilon}(t)=\frac{C_{\mathrm{e}}}{L_{\mathrm{s}}}\left[\varepsilon_{\mathrm{I}}(t)-\varepsilon_{\mathrm{R}}(t)-\varepsilon_{\mathrm{T}}(t)\right]$ (3)
式中：εI(t)、εR(t)、εT(t)分别为入射波、反射波、透射波产生的应变，Ae、Ee为压杆的截面面积和弹性模量，Ce为应力波在压杆中的传播速度，As、Ls分别为试件的初始截面积和初始长度。
选取2个白砂岩标准样、2个煤单体标准样和6个层状岩体试样进行静力学加载，主要用于确定HJC本构模型中的基本力学参数和对比静力加载与动力加载时复合体表现出的力学性能差异。
按试样受冲击波作用方向将复合体分为两组，每组7个，进行动载试验。共设置3个不同速度区间的单轴冲击试验，分别为v=5~7、7~9和9~11 m/s，每个区间2个试样。
由于SHPB试验具有很强的不确定性，每组设置1个层状煤岩复合体作为补充试样。试样按照冲击方向进行分组编号，以SH-1为例，SH代表煤单体作为受冲击波作用的岩样靠近入射杆，1为序号，试样具体参数见表 1。
表 1
表 1 层状煤岩复合体试样具体参数 Tab. 1 Specific parameters of laminated coal-rock composite samples 组号试样编号直径?/mm质量m/g表观密度ρ/(kg·m-3)纵波波速V/(m·s-1)设计速度v/(m·s-1)SH-150.31982 004.782 065低速
SH-250.41982 000.802 100低速
SH-350.01891 925.141 985中速
1SH-450.51951 966.592 085中速
SH-550.01901 935.322 190高速
SH-650.01972 006.632 020高速
SH-750.51901 916.162 100
HS-150.01911 945.512 045低速
HS-250.51891 906.082 215低速
HS-350.91901 901.102 220中速
2HS-450.31951 974.411 885中速
HS-550.31971 994.662 080高速
HS-650.51981 996.842 240高速
HS-750.21971 995.591 945
表 1 层状煤岩复合体试样具体参数 Tab. 1 Specific parameters of laminated coal-rock composite samples
1.3 DYNA模拟样品搭建在动力学试验中，由于材料的局限性，不能直接表征出内部的破裂规律，实验过程对样品具有损坏性且结果具有离散性。只能得到试样的部分宏观参数，不能揭示其内部演变规律。为了得到复合岩体内部损伤特征，结合LS-DYNA软件对SHPB试验开展模拟。
1.3.1 模型参数的选取子弹、输入杆、透射杆选取线弹性材料，模型参数与SHPB试验系统相一致，这里需要特殊说明的是，在本次实验中使用的是纺锤形冲击弹头，可产生半正弦应力波，已有研究表明，这是SHPB实验中最理想的波形，更加适用于脆性岩石[27]。子弹的建模及具体尺寸如图 5所示。
Fig. 5
图 5 纺锤形弹头建模 Fig. 5 Modeling of a spindle-shaped warhead HJC全称为Homquist-Johnson-Cook本构模型，广泛应用于考虑损伤情况下的大应变率加载情况，在动力冲击领域应用较为广泛[28-29]。如图 6所示，HJC本构模型可利用3项多项式状态方程来描述煤单体压力p与体积应变μ的关系，分别是弹性相(OA段)、塑性相(AB段)和材料的致密压实相(BC段)，可充分表征加载过程中的裂隙发育细观机制。
Fig. 6
图 6 HJC本构模型状态方程 Fig. 6 State equation of HJC constitutive model 将HJC本构方程输入搭建完毕的数值模型中，完成加载过程并获取动态应力-应变曲线，与室内试验所得曲线进行验证，对比结果如图 7所示。数值模拟与室内试验结果吻合程度较高，动态应力-应变曲线遵循规律一致，证明本文采取的参数是正确有效的。
Fig. 7
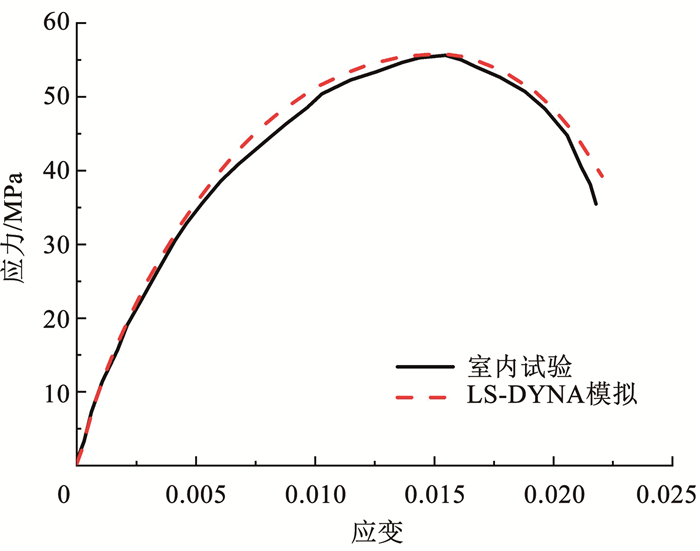图 7 层状复合体室内试验与数值模拟动态应力-应变曲线对比 Fig. 7 Comparison of dynamic stress-strain curves of laminated composites in indoor tests and numerical simulations 在LS-DYNA软件里，HJC模型共有21个参数，本文中HJC试验参数的选取由以下3部分组成：1) 由基本参数测量和静力学试验过程得到的密度、波速、弹性模量、单轴抗压强度、泊松比等；2) 基于1)所得基本力学参数和参数间计算公式推导得到的剪切模量、体积模量、破碎点的体积压力与体积应变等；3) 受限于试验条件，其余参数无法通过试验获取，包括压实点的体积压力与体积应变、3个压力常数、归一化内聚强度、应变率系数、最大归一化强度在内的参数由于其灵敏度较低选取与文献[30-31] 一致的取值，剩余取值则结合参考文献与1)所得力学参数选取与试验所用样品最为接近的力学参数。综上，选定了白砂岩和煤单体的材料参数，如表 2、3所示。
表 2
表 2 白砂岩HJC参数 Tab. 2 HJC parameters of white sandstone ρ0/(kg·m-3)G/MPafc/MPaSmaxD1D2εfminfs2 40148145.170.0410.010.01
T/MPapc/MPaμck1/GPak2/GPak3/GPa
4160.00185-17020860
表 2 白砂岩HJC参数 Tab. 2 HJC parameters of white sandstone
表 3
表 3 煤单体HJC参数 Tab. 3 HJC parameters of coal monomer ρ0/(kg·m-3)G/GPafc/MPaSmaxD1D2εfminfs1 4601.4514.370.02710.010.04
T/MPapc/MPaμck1/GPak2/GPak3/GPa
1.86300.1285-17020860
表 3 煤单体HJC参数 Tab. 3 HJC parameters of coal monomer
1.3.2 有限元模型的建立根据试验的实际尺寸，建立了SHPB试验装置(Solid164)的弹头、压杆和试样单元。接着对模型进行网格剖分，将子弹和输入传输杆径向划分为30份，子弹轴向划分为37份，入射和传输杆轴向划分为250份。为了更好地展现试样的破裂规律，对试样进行精细划分，轴向和径向都划分为60份。试件与压杆之间的接触使用关键字*CONTACT_ERODING_SURFACE_TO_SURFACE定义，此关键字常用于接触表面实体单元失效贯穿，剩下单元继续参与接触的物理问题中，最终的网格划分如图 8所示。在透射杆尾部添加无反射边界模拟原有吸收杆，引入侵蚀关键字*MAT ADD EOSION模拟加压后裂隙的孕育特征。由孙其然等[32]的研究可知，采用压力联合主应变的失效准则可以大幅提高准确性，最终针对煤单体和白砂岩确定不同的侵蚀参数以模拟真实的岩石力学行为。
Fig. 8
图 8 基于LS-DYNA的层状复合体网格划分 Fig. 8 Laminated composite meshing based on LS-DYNA 2 试验结果 2.1 复合体力学性能 2.1.1 静态力学性能由微机控制电液伺服岩石压力试验机测得标准块的基本力学参数，如表 4所示，可以看出，白砂岩相较于煤单体为硬岩，测得的力学参数可直接用于1.3.1节的HJC本构模型参数选取。
表 4
表 4 岩石基本物理力学参数 Tab. 4 Basic physical and mechanical parameters of rock 岩石种类密度ρ/(kg·m-3)波速V/(m·s-1)单轴抗压强度σc/MPa弹性模量G/GPa煤单体1 459.951 797.214.332.43
白砂岩2 401.122 475.045.074.20
表 4 岩石基本物理力学参数 Tab. 4 Basic physical and mechanical parameters of rock
图 9为改变加载方向时得到的应力-应变曲线。试样在达到压缩极限后破损卸压，此过程中，SH复合体与HS复合体峰值应力基本相同，但峰值应变HS复合体大于SH复合体，在达到极限应力时，HS复合体的极限应变更大。由于煤单体的自身构造决定了其更容易达到应力极限，当压力试验机不断加压时，煤单体会由于节理裂隙过多而达到储能极限，裂隙孕育和延伸到贯穿试样后则会瞬间释放弹性能而导致白砂岩紧跟着破碎，即复合体的破碎主要源于煤单体的破碎。HS复合体中的白砂岩更靠近加压端，会吸收更多的能量用于自身裂隙发育，SH复合体则刚好相反，煤单体更易吸收到更多能量而破损。因此，HS复合体会吸收更多能量用于自身破碎，从而产生了更大的极限应变。复合体的单轴抗压强度相较于单一组分有所增强，其增强的幅度取决于较软弱岩石煤单体。
Fig. 9
图 9 层状复合体的单轴压缩应力-应变曲线 Fig. 9 Uniaxial compressive stress-strain curves of laminated composites 2.1.2 动态力学性能图 10为室内试验过程和DYNA模拟过程的层状复合体入射波、反射波和透射波波形。传统SHPB试验输出波形图为电压-时间图，LS-DYNA软件输出波形图为应变-时间图，基于三波法将二者转换为应力-时间图，可以看出，DYNA模拟过程用时较短，但两者总体趋势与结果近似一致，因此，参数下的模拟结果可以与实验结果相匹配。
Fig. 10
图 10 层状复合体典型入射、反射、透射波形 Fig. 10 Typical incident, reflection, and transmission waveforms of laminated composites 图 11分别显示了室内试验与数值模拟的动态应力平衡曲线，动态应力平衡是SHPB实验的前提，可以看出，两者入射应力和反射应力的叠加接近于透射应力，满足动态平衡条件，说明在SHPB冲击载荷下得到的试验数据是有效的。
Fig. 11
图 11 层状复合体动态应力平衡验证 Fig. 11 Verification of dynamic stress balance of laminated composites 引入动态增长因子DIF(dynamic increase factor, fDI) 的概念用于衡量不同冲击方向和速度对层状复合体动态力学性能的影响。2.1.1节测得层状煤岩复合体静态抗压强度为20.67 MPa，动态抗压强度由SHPB试验测得，其主要动态力学参数如表 5所示。
表 5
表 5 层状复合体主要动态力学参数 Tab. 5 Main dynamic mechanical parameters of laminated composites 试样编号密度ρ/(kg·m-3)冲击速度v/(m·s-1)峰值应力fc/MPa峰值应变ε/10-3动态增长因子fDISH-12 004.785.2923.9415.771.16
SH-22 000.806.3831.3920.881.52
SH-31 925.146.6130.4316.561.47
SH-41 966.597.2141.4116.772.00
SH-51 935.329.1945.1725.082.19
SH-62 006.6311.2056.4727.802.73
HS-11 945.515.3631.9014.611.54
HS-21 906.086.1837.5620.631.82
HS-31 901.106.6643.8719.332.12
HS-41 974.418.3346.2017.352.24
HS-51 994.6611.3255.6221.782.69
表 5 层状复合体主要动态力学参数 Tab. 5 Main dynamic mechanical parameters of laminated composites
图 12(a)、(b)和13(a)、(b)分别为室内试验与数值模拟得到的层状岩体不同速度下的动态应力-应变曲线。可以看出，HS复合体与SH复合体受动态载荷时表现出的动态特性基本一致，符合常见脆性岩石应力-应变变化规律。随着速度的增加不断积蓄弹性能，此过程体积被不断压缩，最终到达阈值后试块破碎，弹性能释放，这个过程中，峰值应力和峰值应变都随着速度不断增加。如图 14(a)、(b)所示，随着速度的增加，两种试样的峰值应力整体呈线性增大的趋势。但在相同的冲击速度下，HS复合体的峰值应力都略大于SH复合体，这是由于HS复合体的白砂岩组分波阻抗与压杆的更为接近，有更好的能量传递效果，也会得到更好的动态力学性能结果。不过这种影响作用会随着冲击能量的增大而逐渐衰弱。
Fig. 12
图 12 层状复合体室内试验动态应力-应变曲线 Fig. 12 Dynamic stress-strain curves of laminated composites in indoor tests Fig. 13
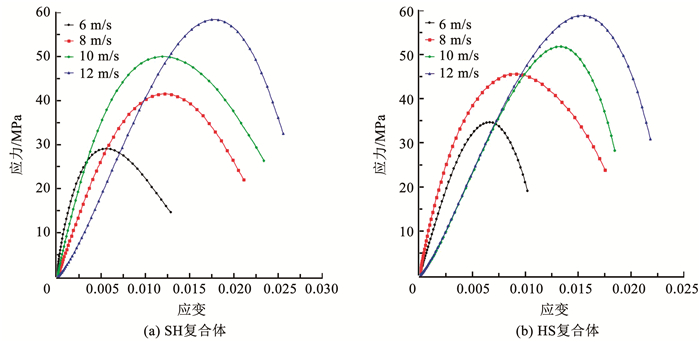图 13 层状复合体数值模拟动态应力-应变曲线 Fig. 13 Numerical simulation of dynamic stress-strain curves for laminated composites Fig. 14
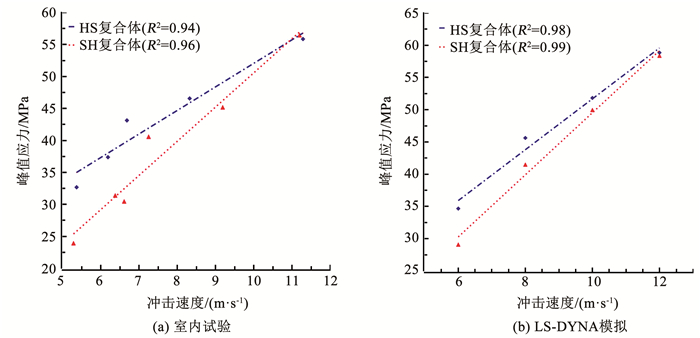图 14 冲击速度与峰值应力的关系 Fig. 14 Relationship between impact velocity and peak stress 2.2 能量耗散分析岩石在破碎过程中，驱动的核心便是能量耗散，能量耗散是一个不可逆的过程[33]。研究层状复合体的能量耗散规律可以帮助了解改变应力波冲击方向与速度时，波阻抗匹配效应产生的影响。在SHPB试验过程中，根据一维弹性波理论，应力波携带能量为
$W_{\mathrm{I}}=\frac{C_{\mathrm{e}} A_{\mathrm{e}}}{E_{\mathrm{e}}} \int \sigma_{\mathrm{I}}^2(t) \mathrm{d} t$ (4)
$W_{\mathrm{R}}=\frac{C_{\mathrm{e}} A_{\mathrm{e}}}{E_{\mathrm{e}}} \int \sigma_{\mathrm{R}}^2(t) \mathrm{d} t $ (5)
$\begin{aligned}W_{\mathrm{T}}=\frac{C_{\mathrm{e}} A_{\mathrm{e}}}{E_{\mathrm{e}}} \int \sigma_{\mathrm{T}}^2(t) \mathrm{d} t\end{aligned}$ (6)
式中：WI、WR、WT分别为入射波、反射波、透射波能量，Ae、Ee为压杆的截面面积和弹性模量，Ce为应力波在压杆中的传播速度，σI(t)、σR(t)、σT(t)分别为t时刻的入射、反射、透射应力。
在不考虑损失的情况下，层状复合岩体在破碎过程中吸收的能量，即耗散能WS为
$W_{\mathrm{S}}=W_{\mathrm{I}}-W_{\mathrm{T}}-W_{\mathrm{R}}$ (7)
式(7)所计算的耗散能包括试样吸收的总能量、试样破碎飞落产生的动能和岩石变形过程中的热能、声能等，平琦等[34]的研究结果显示，后两种能量占比总耗散能不超过5%，因此，在本试验中试样的总吸收能量近似用总耗散能表示。比较单位体积下岩石耗散能密度ωd更能表征岩石破碎吸收能量的多少，耗散能密度ωd为
$\omega_{\mathrm{d}}=\frac{W_{\mathrm{S}}}{V}$ (8)
式中V为层状复合体的体积。
类似地，可以得到入射能密度ωI为
$\omega_{\mathrm{I}}=\frac{W_{\mathrm{I}}}{V}$ (9)
图 15(a)、(b)分别显示了室内试验与数值模拟得到的冲击速度与入射能关系，入射能的大小与冲击速度呈正比关系，并且与岩石试样无关，因此，入射能也可以直接用于表征冲击速度的增加。
Fig. 15
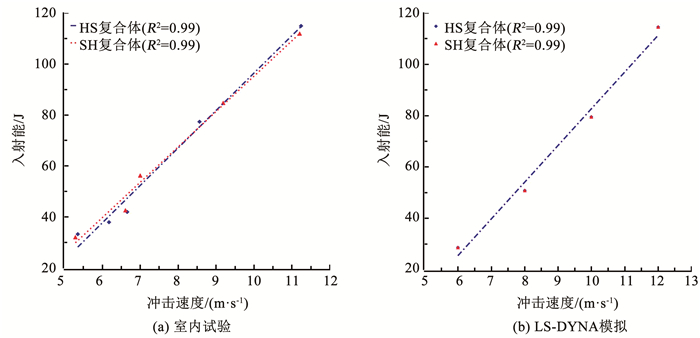图 15 冲击速度与入射能的关系 Fig. 15 Relationship between impact velocity and incident energy 图 16(a)、(b)分别显示了室内试验与数值模拟得到的层状岩体入射能密度与耗散能密度关系。此处应用入射能密度表征冲击波大小，探讨不同冲击波大小下耗散能的变化趋势。两种复合岩体的耗散能密度都与入射能密度呈二次增长关系，并且HS复合体的耗散能密度要始终大于SH复合体。通过耗散能密度的计算公式可以看出，耗散能就是用于岩石破碎能量的量化表征。更高的耗散能密度代表着吸收了更多的能量用于自身破碎，岩样也会得到更好的破碎效果。白砂岩的波阻抗与压杆的波阻抗更为接近，能量传递的效果会比煤单体更优，也就造成了耗散能密度更高。表现在宏观上，相同速度下HS复合体的破碎程度大于SH复合体，随着速度的增加这种趋势逐渐减小。
Fig. 16
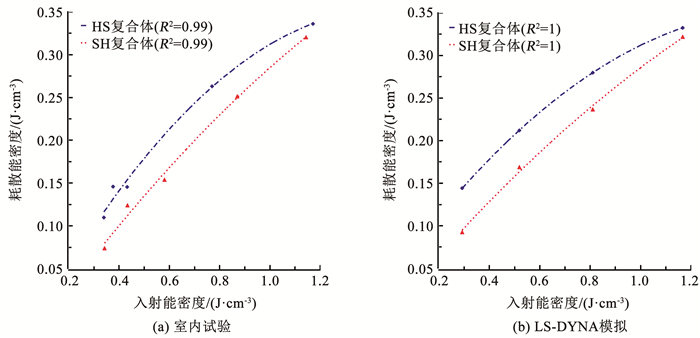图 16 入射能密度与耗散能密度的关系 Fig. 16 Relationship between incident energy density and dissipation energy density 在工程领域，波阻抗效应常常被用于匹配炸药性能，炸药与岩石波阻抗相匹配时可以获得更好的爆破效果。在层状复合体上仍然适用，更优的波阻抗匹配效果会得到更好的破碎效果，其本质便是耗散能的增加。根据能量守能定律、弹性波理论，耗散能会用于自身裂隙的孕育和发展，岩样会先不断储存能量变为弹性能，随着试样破坏作用于另一岩样。煤单体储存弹性能的阈值小于白砂岩，因此，相较SH复合体，HS复合体的白砂岩组分会储存更多弹性能，并且最终作用于煤单体，这也是HS复合体的耗散能大于SH复合体的一个重要原因，并且由于此部分弹性能的释放，煤组分会受到冲击变得更加破碎。
2.3 冲击破坏分形特征岩样破碎所产生的碎块往往是不规则的，分形维数[35]作为分形理论的一个重要分支，可以度量复杂形体的不规则形，是量化离散数据的重要手段。层状复合体作为岩石力学领域常见的岩体，分析其分形特征可以量化地下矿山隧道应力扰动、爆破冲击、掘进等施工过程对复合体的影响作用。白砂岩和煤单体通过环氧树脂胶结在一起，可将其视为一个整体，参考其整体破碎程度将对层状复合体破碎形态研究更加有益。
为了定量描述层状煤岩复合体在动力载荷作用下的破损物分布情况，采用等效边长-粒度分布进行分形维数计算：
$\begin{gathered}D=3-\alpha \end{gathered}$ (10)
$\alpha=\frac{\lg \left(m_{\mathrm{r}} / m_{\mathrm{t}}\right)}{\lg L_{\mathrm{r}}}$ (11)
式中：D为试样的分形维数，α为mr/mt-Lr在双对数坐标下的斜率值，Lr为破损物的等效粒径，mr为等效粒径小于Lr的破损物累计质量，mt为计算尺度内破损物的总质量。
考虑到破损物粒度分析的质量要求，采用粒径分别为1.25、2.5、5、10、15、20、25、30 mm的筛网对破损后的试样进行筛分。针对大于30 mm的破损物通过手工测量获得长、宽和厚度的特征并进行称重，试样破碎后破损物分形计算结果见表 6。
表 6
表 6 层状煤岩复合体破损物粒度分形统计 Tab. 6 Fractal statistics of particle size of damages in laminated coal-rock composites 试样编号冲击速度v/(m·s-1)不同粒径破损物累计质量mr/g总质量mt/g分形维数D< 1.25 mm1.25 mm2.5 mm5 mm10 mm15 mm20 mm25 mm30 mm40 mm50 mm
SH-15.29112126002215101951.90
SH-26.3843111610330449001812.09
SH-36.613481424001712701792.14
SH-47.2197131453441479001912.20
SH-59.19159201714039083001842.32
SH-611.20201016191818462022001982.36
HS-15.3622611143002412601871.94
HS-26.185471071000142001832.11
HS-36.66851214211260108001882.18
HS-48.33139191920261885001932.32
HS-511.32159111610330449001882.36
表 6 层状煤岩复合体破损物粒度分形统计 Tab. 6 Fractal statistics of particle size of damages in laminated coal-rock composites
图 17为冲击速度改变时不同复合体分形维数的变化趋势。分形维数可以用来量化破碎程度，当分形维数较大时，可以比较完全地描述样品的破碎。如图 17所示，在冲击速度较小时，HS复合体的分形维数始终大于SH复合体，这是因为HS波阻抗匹配效应更好，应力波所传递的能量更加有效地被HS复合体吸收并用于自身破碎，这与2.2节得到的能量耗散理论相匹配。当速度增大时，这种增益效果便开始减弱直至最终消失。
Fig. 17
图 17 冲击速度与分形维数的变化关系 Fig. 17 Relationship between impact velocity and fractal dimension 层状复合体分形维数的增大主要有两个来源，分别是白砂岩和煤单体各自粒径的减小。在分形维数统计过程中，煤单体的粒径一般都小于10 mm，白砂岩的粒径一般都大于15 mm。以此为约束条件，圈定煤单体和白砂岩的大致粒径分布范围，再观察不同岩样的粒径集中范围。可以看出，随着速度的增大，煤单体破碎粒径减小得更为明显，能量利用率也更高，而白砂岩能量利用率较低，粒径对速度的敏感程度低。因此，随着速度增加，波阻抗匹配效果更好的HS复合体煤组分破碎的会更加完全，优于SH复合体，导致整体的分形维数也大于SH复合体。不过随着速度的增加，煤组分已经破碎的十分完全，两种岩体分形维数开始逐渐接近。
3 冲击破坏模式 3.1 宏观破坏规律图 18、19为不同冲击速度下，两种层状复合体受到SHPB冲击后的破碎形态。随着冲击速度的增大两种复合体的破坏程度都变得更加剧烈，破碎粒度也变得越来越小。以HS复合体为例，在低速冲击的作用下，白砂岩先产生局部剪切破坏，随着速度增大开始出现贯穿整个试样的劈裂面，直至组分彻底破碎。煤单体则由低速冲击造成的片状破碎逐渐转变为锥形小块度破碎。黏结面的存在使试样裂隙延伸作用影响更大，也会增强交界面处煤单体的强度，具体原因在后面讲述。
Fig. 18
图 18 SH复合体动态冲击破坏形态 Fig. 18 Dynamic impact failure morphology of SH composite Fig. 19
图 19 HS复合体动态冲击破坏形态 Fig. 19 Dynamic impact failure morphology of HS composite 造成煤单体和白砂岩破坏差异的主要原因是内部结构的差异，煤是典型的沉积岩，含有较多缺陷，易沿着内部节理裂隙碎裂，根据格里菲斯理论[36]，裂隙间张拉力会使得煤单体破碎得更为充分。而白砂岩内部结构紧密，碎裂的主要原因是剪切面的形成，整体应力分布发生变化，最终导致破坏，所以，破坏得到的破损物较为规整，粒度也较大。在速度相似时，SH复合体的破碎程度要大于HS复合体，这是由波阻抗匹配效应的不一致造成的。HS复合体拥有更好的匹配效应，会造成能量的充分传递和利用，因此，白砂岩和煤单体都可以得到更多的能量用于自身破碎。
矿山中的动力扰动现象时有发生，从图 18、19中可以观察到，相同程度的动力扰动下，SH复合体的破碎程度远大于HS复合体，并且软弱岩层的损伤更为严重。因此，当动力扰动从软弱岩层方向输入时，应选取更为可靠的维稳措施，以防止生产事故发生。当动力扰动程度较小时，如图 19(a)所示，HS复合体的煤单体和白砂岩组分都存在不同程度损伤，但其整体并未发生严重的崩裂现象，尤其是白砂岩组分，因此，即使试样发生了不同程度的破坏，也并不能代表整体会发生失稳事故。然而如图 18(a) 所示，相同动力扰动水平下，SH复合体整体出现了明显的剪切面和脱落崩裂现象。这种现象在发生岩爆时将更加明显，即SH复合体对于外部动力响应更加敏感，危害也更大，因此，在相同动力扰动水平下，应力输入方向从软-硬岩层输入比硬-软岩层输入发生岩爆的概率更高，需要加强防范。
为洞悉层状复合体在动载下的破碎规律，在LS-DYNA软件上进行了动力冲击模拟。图 20、21分别为HS和SH层状复合体在冲击速度为12 m/s下的破碎时程图，上部为从白砂岩为主面的观察视图，下部为从煤单体为主面的观察视图。可以看出，与实验过程得到的破碎结果较为一致，随着时间的不断增大, 煤单体和白砂岩都趋于更加破碎。由于自身节理裂隙的作用，煤单体在受到压力时会产生极大的剪切力，造成煤单体向外劈裂。白砂岩内部紧密坚硬，受到压力后不会向外劈裂而是更多用于自身裂隙的孕育。结合其他速度下的动力冲击模拟，随着速度的增加，煤单体的破碎程度在不断增加，整体呈粉末状趋势；白砂岩的破裂则大多源自裂隙延伸造成的劈裂面，易形成大块度破碎物。两种复合体整体破碎规律并无太大不同，但在速度相同时，SH复合体的白砂岩组分比HS的白砂岩组分破碎度减弱许多。
Fig. 20
图 20 v=12 m/s时HS复合体破碎时程图 Fig. 20 Shattering time history of HS composite at v=12 m/s Fig. 21
图 21 v=12 m/s时SH复合体破碎时程图 Fig. 21 Shattering time history of SH composite at v=12 m/s 3.2 细观损伤模式图 22为层状复合体破碎后的SEM面扫描电镜图。如图 22(a)所示，煤单体破碎后断面呈层状节理，节理裂隙多、杂且不规整，造成煤单体整体分崩离析的作用力源自试样内部，细观破碎量的积累造成了煤单体的宏观破碎，这是由岩石性质决定的。如图 22(b)所示，环氧树脂胶结作用的存在使两种岩石更容易发生劈裂面的传递，一种岩样的破裂间接导致另一种岩样的破裂。如图 22(c)所示，白砂岩组分破碎后断面较为规整，裂隙少且大，造成组分破裂的作用力来自岩样产生的贯穿劈裂面，从局部劈裂面到贯穿劈裂面，裂隙的发育与延伸致使白砂岩组分宏观破碎。如图 22(d)所示，煤单体内部存在的杂石会干扰内部的应力分布，从而更易沿着杂石产生节理裂隙，这也是内部干扰造成的试样破坏。至此，造成层状岩体破坏的细观机制如下：1)煤组分内部由于存在节理裂隙和杂石，更易产生由内至外的宏观破碎，破碎的主要动力来源是内部裂隙造成的应力分布不均；2)白砂岩组分内部致密稳固，宏观破坏的原因是局部拉应力过大产生局部剪切面，剪切面扩展延伸形成贯穿劈裂面从而造成试样失效破碎；3)两种岩样之间胶结作用的存在改变了交界面的应力分布状态，一种岩样产生的裂隙更易传递至另一个岩样从而造成接连破碎。
Fig. 22
图 22 层状复合体SEM面扫描图 Fig. 22 SEM scanning of laminated composites 为了确定图 22(d)中煤样内呈脉状分布的白色细线杂石成分，分别取白砂岩和煤单体样块进行EDS(能量色散谱仪)面扫描，结果如图 23所示。图 23(a)中，白砂岩中主要元素为Si、O、Al等，无异常成分出现。图 23(b)中，煤单体内呈脉状分布的白色细线主要元素为Ca、O、Si等，经分析成分为石灰石、石英等，为煤单体沉积形成过程中的微量杂质。白砂岩的内部元素分布均匀，并且没有明显的节理裂隙。煤单体则含有较多杂质，受到外力作用时会造成内部应力分布不均匀，并且较易沿着杂石产生局部剪切面，最终碎至粒径较小的破碎物，这与图 22观察到的规律一致。
Fig. 23
图 23 能量色散谱仪面扫描图 Fig. 23 Surface scanning by energy dispersive spectrometer 图 24、25分别为HS复合体和SH复合体经LS-DYNA动力冲击模拟后，沿轴向处做剖面，展示内部破坏规律的轴剖面图。HS复合体中白砂岩组分和煤单体组分破坏并无太大联系，煤单体的破坏主要是内部的节理裂隙发育延伸造成的，所以，表现出来的是多且杂，十分容易从内部就开始坍塌破坏，并引起试样整体的破碎。白砂岩组分则可以很清晰地看到裂隙的发育过程直至最终贯穿整个试样，并且得到的破损物较为规整，不会像煤单体一样呈粉碎状。SH复合体中煤单体靠近接触面部位裂隙的延伸最终造成了白砂岩形成劈裂面直至整体剪切破坏加剧。对比两种复合体，由于波阻抗匹配效应的差距，白砂岩组分在HS复合体中破碎的程度会大于SH复合体，而煤单体受此作用较小。在进行隧道开挖、矿床开拓和爆破等施工作业时，需要着重考虑波阻抗匹配效应的影响，在层状岩体为软硬复合体的情况下，匹配效果更好的复合体的硬岩组分会破碎得更加完全。而匹配效果较差时，硬岩的破碎效果有一部分取决于软岩的破碎程度，而且较易产生破碎不完全的情况。
Fig. 24
图 24 HS复合体剖面破裂时程图 Fig. 24 Time history diagram of cross-section rupture of HS composite Fig. 25
图 25 SH复合体剖面破裂时程图 Fig. 25 Time history diagram of cross-section rupture of SH composite 3.3 复合体破坏过程图 26为HS层状复合体的简化模型，由于环氧树脂的作用，白砂岩和煤单体组分会成为一个整体，不会发生相对移动，在受到力的作用后，黏结作用会对煤单体和白砂岩组分产生相应的约束，这就造成了不同组分的受力情况不同。假设忽略环氧树脂的厚度，E和μ分别代表岩石的弹性模量和泊松比，P1代表受冲击的作用力。由于白砂岩的弹性模量大于煤组分，在边界处白砂岩的横向应变要小于煤单体的，但由于环氧树脂约束作用的存在，岩石交界面会产生约束应力来制约其变形。取交界处的一个小单元作为研究对象，由以上分析可知横向应变更小的白砂岩会受到横向拉应力的作用，而煤单体会受到横向压应力的作用。
Fig. 26
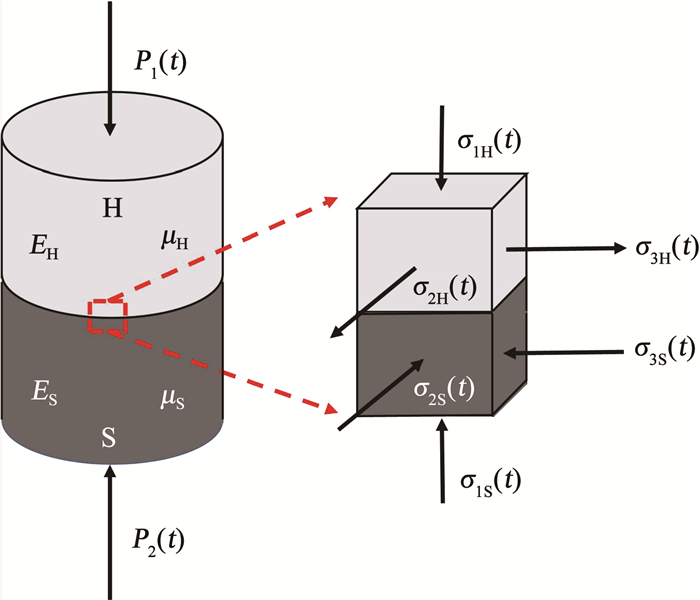图 26 HS层状复合体简化模型 Fig. 26 Simplified model of HS laminated composite 受到冲击载荷的作用，P1和P2是一对大小相同的作用力，这样白砂岩组分就变成了压-拉应力状态，煤单体组分则变成了三向压应力状态。由于交界面以外的岩石没有受到应变约束效应的影响，可以看作只受压应力影响的单元体。按照格里菲斯强度理论[36]，岩石发生破坏的原因是最大拉应力的作用。由于白砂岩组分交界面区域受到三向拉-压应力作用，会比没有受到拉应力作用区域更容易破碎，即其轴压强度小于交界面以外的其他区域。煤组分交界面区域由于受到三向压应力作用，会变得比交界面以外的区域更加不容易破碎，即其轴压强度大于交界面以外的其他区域。同样的莫尔强度理论[37]也会得到类似的结果，交界面的轴压强度会发生变化。因此，交界面处的白砂岩受到三向拉-压应力作用，强度会小于边界区域以外的白砂岩组分；交界面处的煤单体受到三向压应力作用，强度会大于边界区域以外的煤单体组分。同样的分析方法可用于SH层状复合体，由于弹性模量和泊松比没有发生变化，受力状态也不会改变，得到的结论与HS复合体相同。因此，层状复合体的整体强度规律从小到大依次为煤单体非交界面区域、煤单体交界面区域、白砂岩交界面区域、白砂岩非交界面区域，在破坏过程中的顺序也会因此发生变化。
HS复合体在破碎的过程中白砂岩组分交界面会先发生破坏，紧接着非交界面区域和煤单体非交界面区域发生破坏，最终煤单体的边界区域发生破坏。与强度顺序不完全一致是因为在应力波传播的过程中会先经过白砂岩，被吸收一部分弹性能再传至煤单体组分，并不是两者同时受力，因此，顺序也会发生一定的变化。SH复合体则是煤单体的非边界区域先发生破坏，紧接着白砂岩的交界面部分发生破坏，最终煤单体的交界面区域和白砂岩的非交界面发生破坏。而且通过云图的应力分布可知，复合岩体的破坏大都是拉应力造成的，而并非压应力，这与岩石力学中的相应规律一致，符合格里菲斯强度理论。
综上，图 27、28分别为HS复合体和SH复合体轴剖面破坏示意，两者速度相同。HS复合体破坏顺序依次为白砂岩交界面区域、白砂岩非交界面区域、煤单体非交界区域、煤单体交界区域；SH复合体破坏顺序依次为煤单体非交界区域、白砂岩交界区域、煤单体交界区域、白砂岩非交界区域，这与上述强度规律相匹配。SH复合体与HS复合体经入射杆后，应力波传递顺序有所差异，造成了不同复合体的破坏顺序不同。因此，在进行矿山爆破、巷道掘进、支护工作时，需要针对不同需求重点关注层状岩体各区域。例如，在进行造成动力扰动的相关工作时，靠近较硬岩层时，层状岩体需要首先重点关注软-硬岩层交界面失稳，靠近较软岩层时，则需首先重点关注较软岩层非交界面区域。
Fig. 27
图 27 HS复合体轴剖面破坏示意 Fig. 27 Schematic of damage of axial section of HS composite Fig. 28
图 28 SH复合体轴剖面破坏示意 Fig. 28 Schematic of damage of axial section of SH composite 4 结论1) 静态载荷加压情况下，层状煤岩复合体的强度相较于软弱岩石略有增加，方向的改变不会造成强度增加幅度的改变，不过会改变层状煤岩复合体的破裂时程，HS复合体早于SH复合体发生破裂。动态载荷加压情况下，层状煤岩复合体的峰值应力和DIF都随着冲击速度的增加而增大。波阻抗匹配效果的影响下，HS复合体不同速度下的峰值应力都略强于SH复合体，随着速度增大这种影响作用不断减小。
2) SHPB实验中入射能可以用来表征冲击速度，耗散能密度随着入射能密度增大呈二次函数增长，速度相同时，HS复合体耗散能密度略强于SH复合体，HS复合体会吸收更多能量用于自身破碎，随着速度增大这种影响作用不断减小。
3) 随着冲击速度的增加，层状煤岩复合体的分形维数呈增大趋势。在冲击速度较小时, HS复合体的分形维数始终大于SH复合体，这表明HS复合体的破碎程度更高，能量利用效果更好。当速度增大时，这种现象便开始减弱直至最终消失。
4) 随着冲击速度的增大两种复合体的破坏程度都变得更加剧烈，波阻抗匹配效应决定了相同速度下，HS复合体的破坏程度要大于SH复合体。白砂岩多呈剪切状破坏，易形成贯穿岩样的劈裂面；煤单体则多呈粉碎锥形破坏，这种宏观上的破碎来源于细观上裂隙的积累。
5) 受黏结作用的影响，层状煤岩复合体交界处和其他区域强度不一致。层状煤岩复合体整体强度规律从小到大依次为煤单体非交界面区域、煤单体交界面区域、白砂岩交界面区域、白砂岩非交界面区域，复合体的破坏顺序也会因此发生改变，受限于应力波传递过程中的顺序，HS复合体和SH复合体破坏顺序会有所差异。
参考文献
[1] 朱晶晶, 李夕兵, 宫凤强, 等. 冲击载荷作用下砂岩的动力学特性及损伤规律[J]. 中南大学学报(自然科学版), 2012, 43(7): 2701.
ZHU Jingjing, LI Xibing, GONG Fengqiang, et al. Experimental test and damage characteristics of sandstone under uniaxial impact compressive loads[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2701.
[2] 夏开文, 王帅, 徐颖, 等. 深部岩石动力学实验研究进展[J]. 岩石力学与工程学报, 2021, 40(3): 448.
XIA Kaiwen, WANG Shuai, XU Ying, et al. Advances in experimental studies for deep rock dynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 448. DOI:10.13722/j.cnki.jrme.2020.0343
[3] 李夕兵, 周子龙, 叶州元, 等. 岩石动静组合加载力学特性研究[J]. 岩石力学与工程学报, 2008, 27(7): 1387.
LI Xibing, ZHOU Zilong, YE Zhouyuan, et al. Study of rock mechanical characteristics under coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1387. DOI:10.3321/j.issn:1000-6915.2008.07.011
[4] 腾俊洋, 唐建新, 王进博, 等. 层状复合岩体损伤演化规律及分形特征[J]. 岩石力学与工程学报, 2018, 37(增刊1): 3263.
TENG Junyang, TANG Jianxin, WANG Jinbo, et al. The evolution law of the damage of bedded composite rock and its fractal characteristics[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(Sup.1): 3263. DOI:10.13722/j.cnki.jrme.2016.1397
[5] 黄春, 左双英, 王嵩, 等. 层状各向异性岩体的室内单轴压缩试验分析[J]. 长江科学院院报, 2016, 33(5): 58.
HUANG Chun, ZUO Shuangying, WANG Song, et al. Analysis of indoor uniaxial compression test on layered anisotropic rock masses[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(5): 58. DOI:10.11988/ckyyb.20150820
[6] 何忠明, 彭振斌, 曹平, 等. 层状岩体单轴压缩室内试验分析与数值模拟[J]. 中南大学学报(自然科学版), 2010, 41(5): 1906.
HE Zhongming, PENG Zhenbin, CAO Ping, et al. Test and numerical simulation for stratified rock mass under uniaxial compression[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1906.
[7] 王旭一, 黄书岭, 丁秀丽, 等. 层状岩体单轴压缩力学特性的非均质层面影响效应研究[J]. 岩土力学, 2021, 42(2): 581.
WANG Xuyi, HUANG Shuling, DING Xiuli, et al. Study on the effect of inhomogeneous bedding plane on the mechanical properties of uniaxial compression of layered rock mass[J]. Rock and Soil Mechanics, 2021, 42(2): 581. DOI:10.16285/j.rsm.2020.0584
[8] 邓华锋, 李涛, 李建林, 等. 层状岩体各向异性声学和力学参数计算方法研究[J]. 岩石力学与工程学报, 2020, 39(增刊1): 2725.
DENG Huafeng, LI Tao, LI Jianlin, et al. Study on calculation method of anisotropic acoustic and mechanical parameters of layered rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(Sup.1): 2725. DOI:10.13722/j.cnki.jrme.2019.1174
[9] 刘自由, 江学良, 左文贵. 三维应力作用下岩体层面效应分析[J]. 岩土力学, 2010, 31(9): 2835.
LIU Ziyou, JIANG Xueliang, ZUO Wengui. The effect of structure plane in rock mass under tri-axial stress condition[J]. Rock and Soil Mechanics, 2010, 31(9): 2835. DOI:10.16285/j.rsm.2010.09.027
[10] 周科峰, 李宇峙, 柳群义. 层状岩体强度结构面特征的数值分析[J]. 中南大学学报(自然科学版), 2012, 43(4): 1424.
ZHOU Kefeng, LI Yuzhi, LIU Qunyi. Numerical analysis of structure plane characteristic for strength of stratified rock mass[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1424.
[11] 陈宇龙, 张宇宁, 李科斌, 等. 单轴压缩下软硬互层岩石破裂过程的离散元数值分析[J]. 采矿与安全工程学报, 2017, 34(4): 795.
CHEN Yulong, ZHANG Yuning, LI Kebin, et al. Distinct element numerical analysis of failure process of interlayered rock subjected to uniaxial compression[J]. Journal of Mining and Safety Engineering, 2017, 34(4): 795. DOI:10.13545/j.cnki.jmse.2017.04.027
[12] 熊良宵, 李天斌, 杨昌斌, 等. 层状岩体单轴和双轴压缩蠕变特性的数值试验[J]. 吉林大学学报(地球科学版), 2013, 43(5): 1539.
XIONG Liangxiao, LI Tianbin, YANG Changbin, et al. Numerical analysis study on uniaxial and biaxial compression creep tests for interlayered rock mass[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(5): 1539. DOI:10.13278/j.cnki.jjuese.2013.05.024
[13] 熊良宵, 杨林德. 互层状岩体黏弹塑性流变特性的数值分析[J]. 岩石力学与工程学报, 2011, 30(增刊1): 2803.
XIONG Liangxiao, YANG Linde. Numerical analysis for viscoelasto-plastic rheological property of interlayered rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup.1): 2803.
[14] 熊良宵, 杨林德. 互层状岩体的粘弹性流变模型及数值分析[J]. 同济大学学报(自然科学版), 2010, 38(9): 1281.
XIONG Liangxiao, YANG Linde. Viscoelastic rheological model for interlayered rock mass and its numerical analysis[J]. Journal of Tongji University (Natural Science), 2010, 38(9): 1281. DOI:10.3969/j.issn.0253-374x.2010.09.005
[15] 刘运思, 何楚韶, 王世鸣, 等. 冲击荷载下层状板岩拉伸破坏及能耗规律研究[J]. 应用力学学报, 2021, 38(4): 1373.
LIU Yunsi, HE Chushao, WANG Shiming, et al. Study on tensile failure and energy consumption law of layered slate under impact loading[J]. Chinese Journal of Applied Mechanics, 2021, 38(4): 1373. DOI:10.11776/cjam.38.04.B108
[16] 欧雪峰, 张学民, 张聪, 等. 冲击加载下板岩压缩破坏层理效应及损伤本构模型研究[J]. 岩石力学与工程学报, 2019, 38(增刊2): 3503.
OU Xuefeng, ZHANG Xuemin, ZHANG Cong, et al. Study on bedding effect and damage constitutive model of slate under compressive dynamic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(Sup.2): 3503. DOI:10.13722/j.cnki.jrme.2019.0391
[17] 杨仁树, 许鹏, 景晨钟, 等. 冲击荷载下层状砂岩变形破坏及其动态抗拉强度试验研究[J]. 煤炭学报, 2019, 44(7): 2039.
YANG Renshu, XU Peng, JING Chenzhong, et al. Experimental study on the failure and dynamic tensile strength of layered sandstone under impact loads[J]. Journal of China Coal Society, 2019, 44(7): 2039. DOI:10.13225/j.cnki.jccs.2019.0258
[18] 李地元, 邱加冬, 李夕兵. 冲击载荷作用下层状砂岩动态拉压力学特性研究[J]. 岩石力学与工程学报, 2015, 34(10): 2091.
LI Diyuan, QIU Jiadong, LI Xibing. Experimental study on dynamic tensile and compressive properties of bedding sandstone under impact loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(10): 2091. DOI:10.13722/j.cnki.jrme.2015.0519
[19] XIE Beijing, CHEN Dongxin, DING Hao, et al. Numerical simulation of split-hopkinson pressure bar tests for the combined coal-rock by using the holmquist-johnson-cook model and case analysis of outburst[J]. Advances in Civil Engineering, 2020, 2020: 1. DOI:10.1155/2020/8833233
[20] 杜超超, 温森, 孔庆梅. 一维动静组合加载下复合岩样动态力学特性试验研究[J]. 振动与冲击, 2021, 40(21): 168.
DU Chaochao, WEN Sen, KONG Qingmei. Tests for dynamic mechanical properties of composite rock samples under 1D dynamic-static combined loading[J]. Journal of Vibration and Shock, 2021, 40(21): 168. DOI:10.13465/j.cnki.jvs.2021.21.023
[21] 李成杰, 徐颖, 叶洲元. 冲击荷载下类煤岩组合体能量耗散与破碎特性分析[J]. 岩土工程学报, 2020, 42(5): 981.
LI Chengjie, XU Ying, YE Zhouyuan. Energy dissipation and crushing characteristics of coal-rock-like combined body under impact loading[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 981. DOI:10.11779/CJGE202005022
[22] 李成杰, 徐颖, 张宇婷, 等. 冲击荷载下裂隙类煤岩组合体能量演化与分形特征研究[J]. 岩石力学与工程学报, 2019, 38(11): 2231.
LI Chengjie, XU Ying, ZHANG Yuting, et al. Study on energy evolution and fractal characteristics of cracked coal-rock-like combined body under impact loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(11): 2231. DOI:10.13722/j.cnki.jrme.2019.0446
[23] 杨仁树, 李炜煜, 方士正, 等. 层状复合岩体冲击动力学特性试验研究[J]. 岩石力学与工程学报, 2019, 38(9): 1747.
YANG Renshu, LI Weiyu, FANG Shizheng, et al. Experimental study on impact dynamic characteristics of layered composite rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(9): 1747. DOI:10.13722/j.cnki.jrme.2019.0021
[24] DAI Feng, HUANG Sheng, XIA Kaiwen, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar[J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 657. DOI:10.1007/s00603-010-0091-8
[25] 王信刚, 周镇, 赵华, 等. 环氧树脂修复水泥基材料微裂缝的渗透机理[J]. 建筑材料学报, 2021, 24(6): 1200.
WANG Xingang, ZHOU Zhen, ZHAO Hua, et al. Capillary transport mechanism of epoxy resin repairing micro-cracks in cement-based materials[J]. Journal of Building Materials, 2021, 24(6): 1200. DOI:10.3969/j.issn.1007
[26] LI Xibing, LOK T S, ZHAO Jie, et al. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curves for rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(7): 1055. DOI:10.1016/s1365-1609(00)00037-x
[27] 李夕兵, 古德生, 赖海辉. 冲击载荷下岩石动态应力-应变全图测试中的合理加载波形[J]. 爆炸与冲击, 1993, 13(2): 125.
LI Xibing, GU Desheng, LAI Haihui. On the reasonable loading stress waveforms determined by dynamic stress-strain curves of rocks by SHPB[J]. Explosion and Shock Waves, 1993, 13(2): 125.
[28] 李成武, 王金贵, 解北京, 等. 基于HJC本构模型的煤岩SHPB实验数值模拟[J]. 采矿与安全工程学报, 2016, 33(1): 158.
LI Chengwu, WANG Jingui, XIE Beijing, et al. Numerical simulation of SHPB tests for coal by using HJC model[J]. Journal of Mining and Safety Engineering, 2016, 33(1): 158. DOI:10.13545/j.cnki.jmse.2016.01.025
[29] KONG Xiangzhen, FANG Qin, WU Hao, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model[J]. International Journal of Impact Engineering, 2016, 95: 61. DOI:10.1016/j.ijimpeng.2016.04.014
[30] XIE Beijing, YAN Zheng, DU Yujing, et al. Determination of holmquist-johnson-cook constitutive parameters of coal: laboratory study and numerical simulation[J]. Processes, 2019, 7(6): 386. DOI:10.3390/pr7060386
[31] ZHU Hongqing, FANG Shuhao, ZHANG Yilong, et al. Numerical simulation of the dynamic distribution characteristics of the stress, strain and energy of coal mass under impact loads[J]. Scientific Reports, 2020, 10(1): 1. DOI:10.1038/s41598-020-74063-3
[32] 孙其然, 李芮宇, 赵亚运, 等. HJC模型模拟钢筋混凝土侵彻实验的参数研究[J]. 工程力学, 2016, 33(8): 248.
SUN Qiran, LI Ruiyu, ZHAO Yayun, et al. Investigation on parameters of HJC model applied to simulate perforation experiments of reinforced concrete[J]. Engineering Mechanics, 2016, 33(8): 248. DOI:10.6052/j.issn.1000-4750.2014.12.1094
[33] 李地元, 韩震宇, 孙小磊, 等. 含预制裂隙大理岩SHPB动态力学破坏特性试验研究[J]. 岩石力学与工程学报, 2017, 36(12): 2872.
LI Diyuan, HAN Zhenyu, SUN Xiaolei, et al. Characteristics of dynamic failure of marble with artificial flaws under split Hopkinson pressure bar tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2872. DOI:10.13722/j.cnki.jrme.2017.0488
[34] 平琦, 马芹永, 袁璞. 岩石试件SHPB劈裂拉伸试验中能量耗散分析[J]. 采矿与安全工程学报, 2013, 30(3): 401.
PING Qi, MA Qinyong, YUAN Pu. Energy dissipation analysis of stone specimens in SHPB tensile test[J]. Journal of Mining and Safety Engineering, 2013, 30(3): 401.
[35] 赵国彦, 邓青林, 李夕兵, 等. 基于EMD和形态分形维数的微震波形识别[J]. 中南大学学报(自然科学版), 2017, 48(1): 162.
ZHAO Guoyan, DENG Qinglin, LI Xibing, et al. Recognition of microseismic waveforms based on EMD and morphological fractal dimension[J]. Journal of Central South University (Science and Technology), 2017, 48(1): 162. DOI:10.11817/j.issn.1672-7207.2017.01.023
[36] BRACE W F. An extension of the Griffith theory of fracture to rocks[J]. Journal of Geophysical Research, 1960, 65(10): 3477. DOI:10.1029/jz065i010p03477
[37] LABUZ J F, ZANG A. Mohr-Coulomb failure criterion[J]. Rock Mechanics and Rock Engineering, 2012, 45(6): 975. DOI:10.1007/s00603-012-0281-7
