初始地下水对浅层边坡降雨入渗及稳定性影响

赵宇^1,2,3,马朋博^1,2,梁腾^1,2,3,刘准^1,2,吕庆¹

(1.浙江大学 建筑工程学院,杭州 310058;2.软弱土与环境土工教育部重点实验室(浙江大学),杭州 310058; 3.浙江大学 超重力研究中心,杭州 310058)



摘要:

浙江省山地丘陵地区浅层边坡土层大多存在稳定的初始地下水,从而导致土体含水率分布复杂、降雨入渗和稳定性分析难度大。为此,根据土体非饱和特性确定考虑初始地下水影响的坡体含水率指数分布模型,根据雨强与土体饱和渗透系数的对比关系将降雨分为弱降雨和强降雨两类工况,基于Green-Ampt入渗模型及水量平衡原理推导考虑初始地下水影响的浅层边坡降雨入渗物理方程解析解；结合浅层无限边坡模型,分析考虑初始地下水影响的浅层边坡在降雨作用下的稳定性；当假定坡体含水率均匀分布时,改进模型可近似退化为传统模型；当坡体含水率呈指数分布时,通过数值模拟验证改进模型的有效性。结果表明:当浅层边坡基岩上部土层存在初始地下水时,降雨导致的失稳将发生在基岩面处,且失稳时间早于传统模型的预测结果；弱降雨工况下,雨强提高导致边坡触发失稳的时间呈近指数关系快速缩短；强降雨工况下,当不考虑坡面径流对入渗的促进作用时,雨强提高导致边坡触发失稳时间缩短,速度趋于平缓。

关键词:  降雨入渗  Green-Ampt模型  湿润锋  浅层边坡  稳定性

DOI：10.11918/202207118

分类号:P642.22

文献标识码:A

基金项目:浙江省重点研发计划(2021C03159)；国家自然科学基金(9,1,42277132)



Rainfall infiltration and stability of shallow slope considering initial groundwater

ZHAO Yu^1,2,3,MA Pengbo^1,2,LIANG Teng^1,2,3,LIU Zhun^1,2,Lü Qing¹

(1.College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China; 2.Key Laboratory of Soft Soils and Geoenvironmental Engineering (Zhejiang University), Ministry of Education, Hangzhou 310058, China; 3. Center for Hypergravity Experimental and Interdisciplinary Research, Zhejiang University, Hangzhou 310058, China)

Abstract:

Stable initial groundwater exists in most shallow slopes in mountainous and hilly areas of Zhejiang province, which leads to complex distribution of soil water content and difficulty of rainfall infiltration process and slope stability analysis. Considering the characteristics of unsaturated soil, the exponential distribution model of water content of slope under initial groundwater was determined. The rainfall condition was divided into weak and heavy rainfall according to the relationship between rainfall intensity and soil saturated permeability coefficient. On the basis of the Green-Ampt infiltration model and water balance principle, the analytical solution of governing equations for rainfall infiltration of shallow slope with groundwater was derived for the two conditions. Combined with the shallow infinite slope model, the stability of shallow slope under rainfall was analyzed considering the influence of initial groundwater. The modified model could be approximately degenerated into the traditional model when the initial water content was uniformly distributed. When the initial water content was in exponential distribution, the effectiveness of the modified model was verified through numerical simulation. Results showed that shallow slope failure induced by rainfall occurred near the bedrock surface when groundwater existed in the soil layer over the bedrock in shallow slope, and the failure time was prior to that predicted by the traditional model. Under weak rainfall conditions, the failure time was nearly exponentially shortened with the increase in rainfall intensity. Under heavy rainfall conditions, the failure time tended to be stable when the rainfall intensity was increased, on the condition that the promoting effect of slope surface runoff on infiltration was not considered.

Key words:  rainfall infiltration  Green-Ampt model  wetting front  shallow slope  stability


赵宇, 马朋博, 梁腾, 刘准, 吕庆. 初始地下水对浅层边坡降雨入渗及稳定性影响[J]. 哈尔滨工业大学学报, 2023, 55(6): 61-70. DOI: 10.11918/202207118.
ZHAO Yu, MA Pengbo, LIANG Teng, LIU Zhun, Lü Qing. Rainfall infiltration and stability of shallow slope considering initial groundwater[J]. Journal of Harbin Institute of Technology, 2023, 55(6): 61-70. DOI: 10.11918/202207118.
基金项目 浙江省重点研发计划(2021C03159)；国家自然科学基金(52178359，51988101，42277132) 作者简介 赵宇(1982—)，男，教授，博士生导师 通信作者 梁腾，tliang@zju.edu.cn 文章历史 收稿日期: 2022-07-26



Abstract            Full text            Figures/Tables            PDF


初始地下水对浅层边坡降雨入渗及稳定性影响
赵宇^1,2,3, 马朋博^1,2, 梁腾^1,2,3, 刘准^1,2, 吕庆¹    
1. 浙江大学 建筑工程学院，杭州 310058;
2. 软弱土与环境土工教育部重点实验室(浙江大学)，杭州 310058;
3. 浙江大学 超重力研究中心，杭州 310058

收稿日期: 2022-07-26; 录用日期: 2022-09-26; 网络首发日期: 2022-11-03
基金项目: 浙江省重点研发计划(2021C03159)；国家自然科学基金(52178359，51988101，42277132)
作者简介: 赵宇(1982—)，男，教授，博士生导师
通信作者: 梁腾，tliang@zju.edu.cn


摘要: 浙江省山地丘陵地区浅层边坡土层大多存在稳定的初始地下水，从而导致土体含水率分布复杂、降雨入渗和稳定性分析难度大。为此，根据土体非饱和特性确定考虑初始地下水影响的坡体含水率指数分布模型，根据雨强与土体饱和渗透系数的对比关系将降雨分为弱降雨和强降雨两类工况，基于Green-Ampt入渗模型及水量平衡原理推导考虑初始地下水影响的浅层边坡降雨入渗物理方程解析解；结合浅层无限边坡模型，分析考虑初始地下水影响的浅层边坡在降雨作用下的稳定性；当假定坡体含水率均匀分布时，改进模型可近似退化为传统模型；当坡体含水率呈指数分布时，通过数值模拟验证改进模型的有效性。结果表明：当浅层边坡基岩上部土层存在初始地下水时，降雨导致的失稳将发生在基岩面处，且失稳时间早于传统模型的预测结果；弱降雨工况下，雨强提高导致边坡触发失稳的时间呈近指数关系快速缩短；强降雨工况下，当不考虑坡面径流对入渗的促进作用时，雨强提高导致边坡触发失稳时间缩短，速度趋于平缓。
关键词: 降雨入渗    Green-Ampt模型    湿润锋    浅层边坡    稳定性    
Rainfall infiltration and stability of shallow slope considering initial groundwater
ZHAO Yu^1,2,3, MA Pengbo^1,2, LIANG Teng^1,2,3, LIU Zhun^1,2, Lü Qing¹    
1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China;
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering (Zhejiang University), Ministry of Education, Hangzhou 310058, China;
3. Center for Hypergravity Experimental and Interdisciplinary Research, Zhejiang University, Hangzhou 310058, China



Abstract: Stable initial groundwater exists in most shallow slopes in mountainous and hilly areas of Zhejiang province, which leads to complex distribution of soil water content and difficulty of rainfall infiltration process and slope stability analysis. Considering the characteristics of unsaturated soil, the exponential distribution model of water content of slope under initial groundwater was determined. The rainfall condition was divided into weak and heavy rainfall according to the relationship between rainfall intensity and soil saturated permeability coefficient. On the basis of the Green-Ampt infiltration model and water balance principle, the analytical solution of governing equations for rainfall infiltration of shallow slope with groundwater was derived for the two conditions. Combined with the shallow infinite slope model, the stability of shallow slope under rainfall was analyzed considering the influence of initial groundwater. The modified model could be approximately degenerated into the traditional model when the initial water content was uniformly distributed. When the initial water content was in exponential distribution, the effectiveness of the modified model was verified through numerical simulation. Results showed that shallow slope failure induced by rainfall occurred near the bedrock surface when groundwater existed in the soil layer over the bedrock in shallow slope, and the failure time was prior to that predicted by the traditional model. Under weak rainfall conditions, the failure time was nearly exponentially shortened with the increase in rainfall intensity. Under heavy rainfall conditions, the failure time tended to be stable when the rainfall intensity was increased, on the condition that the promoting effect of slope surface runoff on infiltration was not considered.
Keywords: rainfall infiltration    Green-Ampt model    wetting front    shallow slope    stability    
近年来，中国滑坡灾害数量一直呈上升趋势，其中50%以上由极端降雨直接诱发^[1]，浙江省作为中国降雨型滑坡最频发的地区之一，地下水资源丰富且分布复杂^[2]；由降雨引发的滑坡深度一般较浅，滑面通常为与坡面平行的湿润锋面^[3]。一般认为，降雨入渗会使边坡湿润层土体基质吸力消失、重度增加，进而导致土体抗滑力减小、下滑力增大；当土体抗滑力难以维持边坡稳定时即会发生失稳^[4-5]。

目前，对于非饱和土入渗过程的分析主要有以Kostiakov模型和Horton模型等为代表的经验方程模型^[6]、以Iverson等研究为代表的Richard渗流理论模型^[7-8]和Green等^[9]基于毛细理论提出的薄层积水入渗模型(Green-Ampt模型)。其中，Green-Ampt(GA)模型假设土体初始含水率均匀分布，且入渗时存在明确的湿润锋面，锋面上下两侧土体含水率分别为饱和含水率和初始含水率，忽略土体从饱和含水率到初始含水率的过渡区域；由于GA模型物理意义明确且形式简单，近年来，大量学者针对其适用范围及主要参数确定等方面开展研究。Chen等^[10]在GA模型的基础上推导了考虑坡度的边坡降雨入渗模型，该模型假设土体初始含水率均匀分布且湿润层土体为饱和状态；Gavin等^[11]的改进GA模型认为降雨后边坡湿润层土体含水率并未饱和并假定土体基质吸力沿深度线性变化；李宁等^[12]认为在产生径流前湿润层土体未饱和，提出采用非饱和土Van Genuchten(VG)模型确定湿润层土体含水率；马世国等^[13]研究了强降雨和地下水共同作用下的入渗模型，但未考虑坡角和弱降雨工况对于湿润锋推移过程的影响；张洁等^[14]推导了斜坡初始吸力为三角形和梯形分布的改进GA模型，其基于Runge-Kutta原理的数值求解过程复杂；简文星等^[15]研究了坡体含水率沿深度近似为直线——指数曲线分布的降雨入渗模型。可见，现有研究一般采用纯数学方程描述模型边坡土体初始含水率/基质吸力的分布，难以准确反映地下水富集地区坡体初始含水率真实分布情况；同时，稳定性分析时一般认为湿润锋处为潜在滑动面，忽略了由于初始地下水影响提前在基岩面处失稳的可能性，难以准确评价浙江省山地丘陵地区基岩型浅层滑坡灾害致灾机制。

综上，首先基于浅层边坡地下水分布特征及土体非饱和特性，提出考虑初始地下水影响的坡体含水率指数分布模型；基于GA入渗模型及水量平衡原理推导了考虑初始地下水影响的浅层边坡在弱/强两种降雨工况下入渗方程解析解；通过与传统模型和数值模拟结果对比，验证了本文坡体含水率分布模型和降雨入渗方程解析解的有效性；最后，结合浅层无限边坡模型，对比分析了边坡在湿润锋和基岩面两个潜在危险滑动面处的稳定性演化规律。

1 考虑初始地下水影响的浅层边坡降雨入渗过程分析 1.1 考虑初始地下水影响的坡体含水率分布浅层边坡下覆弱透水基岩层，基岩上部土体中大多存在稳定的初始地下水，非饱和土毛细作用使土体含水率分布呈现从坡面到基岩面逐渐增大的趋势(图 1)。Baum等^[16]研究表明，当存在地下水时，坡面到地下水位之间的土体含水率分布可以参照Gardner等^[17]提出的非饱和土土-水特征曲线(SWCC)模型进行改进，其模型为

$\theta=\theta_{\mathrm{r}}+\left(\theta_{\mathrm{s}}-\theta_{\mathrm{r}}\right) \mathrm{e}^{-\alpha \psi^*}$ (1)

Fig. 1
图 1 考虑初始地下水影响的坡体含水率分布 Fig. 1 Water content distribution of slope considering initial groundwater


式中：θ为体积含水率；θ_r为残余体积含水率；θ_s为饱和体积含水率；α为对SWCC曲线拟合得到的参数；ψ为基质吸力水头，且ψ^*=ψ－ψ₀，令ψ₀=1/α以使该SWCC模型具有良好拟合效果^[18]，其中，1/α表示地下水位线以上的毛细饱和带高度。

假定边坡土体基质吸力水头ψ与垂直于坡面方向的深度z存在线性关系^[19]，即

$\psi=H_{\mathrm{w}}-z$ (2)

式中H_w为地下水深度。

因此，坡面到地下水毛细饱和带之间的土体体积含水率分布可表示为指数分布形式，即

$\theta_{z, i}=\theta_{\mathrm{A}}+\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)} \mathrm{e}^{\alpha z}$ (3)

式中θ_A为根据现场实测数据或数值模拟确定的拟合参数。

1.2 考虑初始地下水影响的降雨入渗解析解边坡降雨入渗是一个二维问题，但在浅层边坡的降雨入渗及稳定性分析时，为求解方便，常将该过程简化为一维问题^{[8, 11, 14]}。假定浅层边坡坡度为β，基岩面以上土层存在稳定的初始地下水，且地下水位与基岩面平行，如图 2所示。下面根据降雨强度q与土体饱和渗透系数k_s的大小关系分为弱降雨和强降雨工况分别进行分析。

Fig. 2
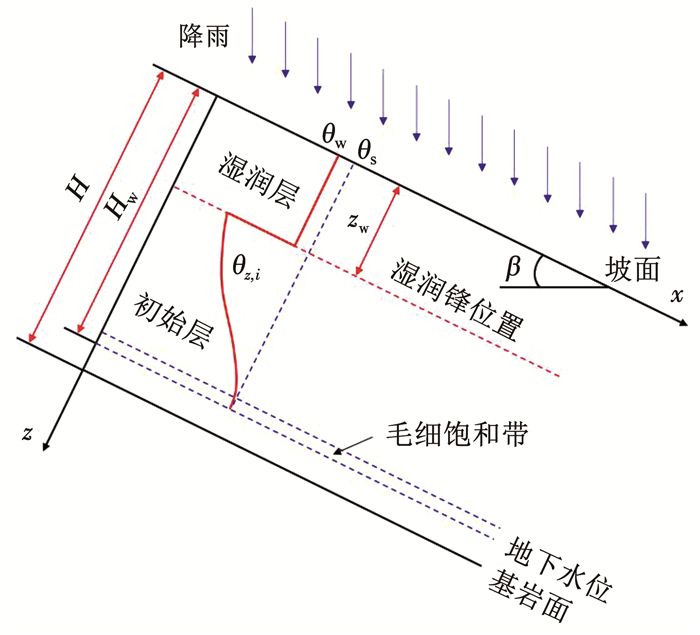图 2 考虑初始地下水影响的浅层边坡降雨入渗模型 Fig. 2 Rainfall infiltration model for shallow slope considering initial groundwater


1.2.1 弱降雨工况(q≤k_s)当降雨强度q小于或等于土体饱和渗透系数k_s时，降雨全部入渗到坡体内部，此时降雨入渗率i(t)为

$i(t)=q \cos \beta$ (4)

由水量平衡原理^[20]，降雨时间t内坡面法向累计入渗量I等于坡体在该方向体积含水率的增量，即

$I=q t \cos \beta=\int_0^{z_{\mathrm{w}}}\left(\theta_{\mathrm{w}}-\theta_{z, i}\right) \mathrm{d} z$ (5)

式中：z_w为降雨时间t对应的湿润锋推移深度，θ_w为湿润层土体体积含水率。根据李宁等^[12]提出的方法：由非饱和土渗透系数方程与降雨入渗率的对应关系求得湿润层土体基质吸力水头ψ，将ψ代入土体含水率-基质吸力关系曲线模型可得降雨强度q对应的湿润层土体体积含水率θ_w，该方法中描述非饱和土渗透系数和计算θ_w的方程^[21]如下：

$k(\psi)=k_{\mathrm{s}} \frac{\left\{1-\left(\alpha_{\mathrm{vg}} \psi\right)^{n-1}\left[1+\left(\alpha_{\mathrm{vg}} \psi\right)^n\right]^{-m}\right\}^2}{\left[1+\left(\alpha_{\mathrm{vg}} \psi\right)^n\right]^{m / 2}}$ (6)

$\theta_{\mathrm{w}}(\psi)=\theta_{\mathrm{r}}+\frac{\theta_{\mathrm{s}}-\theta_{\mathrm{r}}}{\left[1+\left(\alpha_{\mathrm{vg}} \psi\right)^n\right]^m}$ (7)

式中：α_vg、n和m为与SWCC曲线有关的拟合参数，m=1－1/n。

将式(3)代入式(5)，可得

$\int_0^{z_{\mathrm{w}}}\left[\theta_{\mathrm{w}}-\theta_{\mathrm{A}}-\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)} \mathrm{e}^{\alpha z}\right] \mathrm{d} z=q t \cos \beta$ (8)

对式(8)积分即得当存在初始地下水时弱降雨工况下降雨时间t与湿润锋推移深度z_w的关系，为

$t=\frac{z_{\mathrm{w}}\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)-\frac{1}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{w}}}-1\right)}{q \cos \beta}$ (9)

1.2.2 强降雨工况(q＞k_s)当降雨强度q大于土体饱和渗透系数k_s时，降雨过程应根据降雨入渗率i(t)的变化分为两个阶段：降雨强度控制阶段和土体入渗能力控制阶段，如图 3所示。

Fig. 3
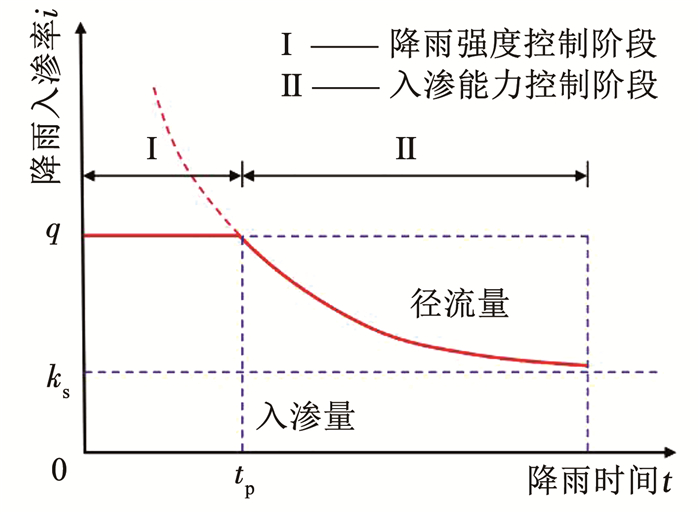图 3 强降雨工况下入渗率与降雨时间关系曲线 Fig. 3 Infiltration rate over rainfall duration under heavy rainfall conditions


降雨初期(0≤t≤t_p)，降雨强度q小于土体入渗能力，即降雨强度控制阶段，此阶段降雨入渗率i(t)同式(4)，降雨时间t与湿润锋推移深度z_w的关系同式(9)。

随着降雨持续进行，土体入渗能力不断减小至小于降雨强度后(t≥t_p)，坡面产生径流，即土体入渗能力控制阶段，此阶段降雨入渗率i(t)为

$i(t)=k_{\mathrm{s}} \frac{z_{\mathrm{w}} \cos \beta+s_{\mathrm{f}}}{z_{\mathrm{w}}}$ (10)

式中s_f为湿润锋处基质吸力水头，可按下式计算^[22]：

$s_{\mathrm{f}}=\frac{1}{k_{\mathrm{s}}} \int_0^{\psi_i} k(\psi) \mathrm{d} \psi$ (11)

式中：ψ_i为土体体积含水率θ_i对应的基质吸力水头，k(ψ)为渗透系数方程即式(6)。

坡面开始产生径流时，降雨强度q沿垂直于坡面z方向的分量刚好等于该方向土体入渗能力大小，令开始产生径流时的湿润锋推移深度为z_p，则有

$q \cos \beta=k_{\mathrm{s}} \frac{z_{\mathrm{p}} \cos \beta+s_{\mathrm{f}}}{z_{\mathrm{p}}}$ (12)

求解式(12)，可得

$z_{\mathrm{p}}=\frac{s_{\mathrm{f}}}{q \cos \beta / k_{\mathrm{s}}-\cos \beta}$ (13)

令开始产生径流时的累计入渗量为I_p，则有

$I_{\mathrm{p}}=\int_0^{z_{\mathrm{p}}}\left(\theta_{\mathrm{w}}-\theta_{z, i}\right) \mathrm{d} z$ (14)

将式(3)代入式(14)并积分，可得

$I_{\mathrm{p}}=z_{\mathrm{p}}\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)-\frac{1}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{p}}}-1\right)$ (15)

则坡面产生径流时间t_p为

$t_{\mathrm{p}}=\frac{I_{\mathrm{p}}}{q \cos \beta}$ (16)

将式(15)代入式(16)，可得

$t_{\mathrm{p}}=\frac{z_{\mathrm{p}}\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)-\frac{1}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{p}}}-1\right)}{q \cos \beta}$ (17)

当t＞t_p时，由水量平衡原理可得

$\begin{aligned}I= & q t_{\mathrm{p}} \cos \beta+\int_{t_{\mathrm{p}}}^t k_{\mathrm{s}} \frac{z_{\mathrm{w}}(t) \cos \beta+s_{\mathrm{f}}}{z_{\mathrm{w}}(t)} \mathrm{d} t= \\& \int_0^{z_{\mathrm{w}}}\left(\theta_{\mathrm{w}}-\theta_{z, i}\right) \mathrm{d} z\end{aligned}$ (18)

对于浅层边坡，参照文献[10]的假定，可认为

$\begin{gathered}\int_{t_{\mathrm{p}}}^t k_{\mathrm{s}} \frac{z_{\mathrm{w}}(t) \cos \beta+s_{\mathrm{f}}}{z_{\mathrm{w}}(t)} \mathrm{d} t \approx \\\frac{1}{2}\left(q \cos \beta+k_{\mathrm{s}} \frac{z_{\mathrm{w}} \cos \beta+s_{\mathrm{f}}}{z_{\mathrm{w}}}\right)\left(t-t_{\mathrm{p}}\right)\end{gathered}$ (19)

将式(19)代入式(18)，并对式(18)积分后整理可得当存在初始地下水时，强降雨工况下土体入渗能力控制阶段降雨时间t与湿润锋推移深度z_w的关系为

$t=t_{\mathrm{p}}+\frac{2\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)\left(z_{\mathrm{w}}-z_{\mathrm{p}}\right)+\frac{2}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{p}}}-\mathrm{e}^{\alpha z_{\mathrm{w}}}\right)}{q \cos \beta+k_{\mathrm{s}}\left(\cos \beta+\frac{s_{\mathrm{f}}}{z_{\mathrm{w}}}\right)}$ (20)

综上，当存在初始地下水时，强降雨工况下降雨时间t与湿润锋推移深度z_w的关系为

$t\left\{ \begin{array}{l}\frac{z_{\mathrm{w}}\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)-\frac{1}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{w}}}-1\right)}{q \cos \beta}, 0 \leqslant t \leqslant t_{\mathrm{p}}\\t_{\mathrm{p}}+\frac{2\left(\theta_{\mathrm{w}}-\theta_{\mathrm{A}}\right)\left(z_{\mathrm{w}}-z_{\mathrm{p}}\right)+\frac{2}{\alpha}\left(\theta_{\mathrm{s}}-\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)}\left(\mathrm{e}^{\alpha z_{\mathrm{p}}}-\mathrm{e}^{\alpha z_{\mathrm{w}}}\right)}{q \cos \beta+k_{\mathrm{s}}\left(\cos \beta+\frac{s_{\mathrm{f}}}{z_{\mathrm{w}}}\right)}, t>t_{\mathrm{p}}\end{array} \right.$ (21)

2 考虑初始地下水影响的浅层边坡稳定性分析当浅层边坡下覆基岩处土层存在初始地下水，且降雨为诱发滑坡主要因素时，根据文献[13]的结论，应同时考虑基岩面处与湿润锋处两个潜在危险滑动面(图 4)。下面将上文改进降雨入渗模型与浅层无限边坡模型结合，分别分析两个潜在危险滑动面的安全系数随降雨时间的变化关系。

Fig. 4
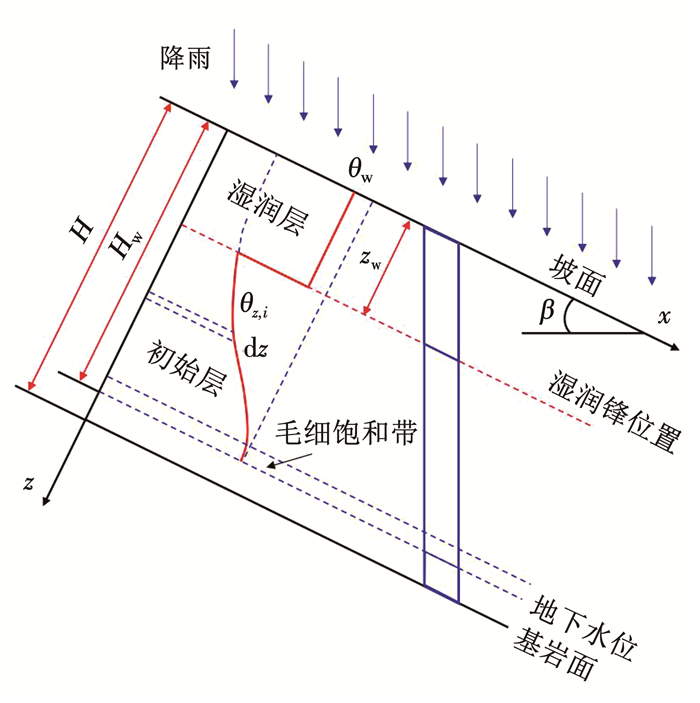图 4 浅层边坡稳定性分析 Fig. 4 Analysis diagram of shallow slope stability


2.1 湿润锋处稳定性分析湿润锋位置z_w随降雨时间t的增加而不断向下推移，考虑湿润锋处作为一个潜在危险滑动面，如图 5(a)所示，采用安全系数F_s评价边坡稳定性，其定义为土体抗滑力与下滑力之比，其中，抗滑力采用Fredlund等^[23]提出的土体抗剪强度理论求解，下滑力为湿润层土体重度沿坡面方向的分量，则湿润锋处安全系数可表示为

$F_{\mathrm{s}}=\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{m}}}=\frac{c^{\prime}+\left(\sigma_{\mathrm{n}}-u_{\mathrm{a}}\right) \tan \varphi^{\prime}+\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right) \tan \varphi^{\mathrm{b}}}{\gamma_{\mathrm{t}} z_{\mathrm{w}} \sin \beta}$ (22)

Fig. 5
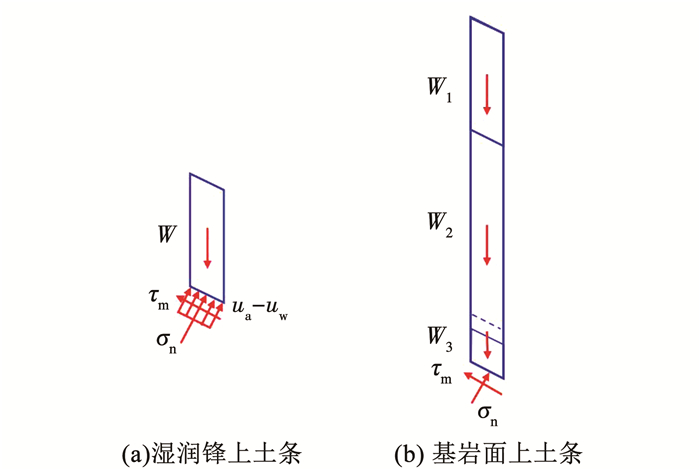图 5 单宽土条分析 Fig. 5 Analysis diagram of soil strip


式中：τ_f为土体抗滑力；τ_m为土体下滑力；c′和φ′分别为土的有效黏聚力和有效内摩擦角；σ_n为单宽土条底部正应力，σ_n=γ_tz_wcos β；γ_t为湿润层土体重度；u_a为孔隙气压力，假定为0；u_w为孔隙水压力；(u_a－u_w)为土体基质吸力，当土体饱和时，该项为0；tan φ^b为抗剪强度随基质吸力(u_a－u_w)增加而增加的速率，根据Vanapalli等^[24]提出的φ^b与土体体积含水率间的经验模型可表示为

$\tan \varphi^{\mathrm{b}}=\left(\frac{\theta-\theta_{\mathrm{r}}}{\theta_{\mathrm{s}}-\theta_{\mathrm{r}}}\right) \tan \varphi^{\prime}$ (23)

2.2 基岩面处稳定性分析当浅层边坡基岩面以上土层存在稳定的初始地下水时，由非饱和土毛细作用导致的毛细饱和带至基岩面之间的土体呈近饱和状态，基质吸力基本消失；对基岩面以上单宽土条沿深度分为3部分进行分析，如图 5(b)所示。

第1部分：坡面到湿润锋面之间(0≤z≤z_w)

$W_1=\gamma_{\mathrm{sat}} \frac{z_{\mathrm{w}}}{\cos \beta}$ (24)

式中γ_sat为土体饱和重度。

第2部分：湿润锋面到毛细饱和带之间(z_w≤z≤H_w－1/α)，在其任意深度z处取dz段分析，则dz段自重应力可表示为

$\mathrm{d} W_2=\gamma_{z, i} \frac{1}{\cos \beta} \mathrm{d} z$ (25)

式中γ_{z, i}为深度z处土体重度。

由土体基本物理特性可推得

$\begin{gathered}\rho_{z, i}=\theta_{z, i} \rho_{\mathrm{w}}+\rho_{\mathrm{s}}\left(1-\frac{C}{V}\right) \end{gathered}$ (26)

$\gamma_{z, i}=\rho_{z, i} g$ (27)

式中：ρ_{z, i}为深度z处土体密度；ρ_w为水的密度；ρ_s为土粒密度；C/V为土体孔隙体积与总体积之比，假设入渗过程中土体含水率的变化不引起土体体积的变化及土颗粒骨架的变形^[23]。

将式(26)、(27)代入式(25)，得

$\mathrm{d} W_2=\frac{g}{\cos \beta}\left[\theta_{z, i} \rho_{\mathrm{w}}+\rho_{\mathrm{s}}\left(1-\frac{C}{V}\right)\right] \mathrm{d} z$ (28)

将式(3)代入式(28)，并积分可得

$\begin{aligned}W_2= & \frac{g}{\cos \beta} \int_{z_{\mathrm{w}}}^{H_{\mathrm{w}}-\frac{1}{\alpha}}\left\{\left[\theta_{\mathrm{A}}+\left(\theta_{\mathrm{s}}-\right.\right.\right. \\& \left.\left.\left.\theta_{\mathrm{A}}\right) \mathrm{e}^{\left(1-\alpha H_{\mathrm{w}}\right)} \mathrm{e}^{\alpha z}\right] \rho_{\mathrm{w}}+\rho_{\mathrm{s}}\left(1-\frac{C}{V}\right)\right\} \mathrm{d} z\end{aligned}$ (29)

第3部分：毛细饱和带到基岩面之间(H_w－1/α≤ z≤H)

$W_3=\gamma^{\prime} \frac{H-H_{\mathrm{w}}+\frac{1}{\alpha}}{\cos \beta}$ (30)

式中γ′为土体有效重度。

基岩面以上单宽土条底部正应力与切应力可分别表示为

$\begin{gathered}\sigma_{\mathrm{n}}=\sum W_i \cos ^2 \beta \end{gathered}$ (31)

$\tau_{\mathrm{m}}=\sum W_i \cos \beta \sin \beta$ (32)

式中∑W_i=W₁+W₂+W₃。

因此，基岩面处安全系数可表示为

$F_{\mathrm{s}}=\frac{\tau_{\mathrm{f}}}{\tau_{\mathrm{m}}}=\frac{c^{\prime}+\sum W_i \cos ^2 \beta \tan \varphi^{\prime}}{\sum W_i \cos \beta \sin \beta}$ (33)

3 模型验证与分析首先将改进模型计算结果分别与传统模型和数值模拟结果对比，验证改进模型的有效性；然后利用改进模型分别计算不同降雨强度下湿润锋推移深度与降雨时间的关系；最后对存在初始地下水影响的浅层边坡在降雨条件下的稳定性进行了讨论。

浙江省山地丘陵地区降雨型滑坡基岩上覆土层深度大多在4~8 m，且坡度集中在25°~35°^[25]。因此，假定一浅层边坡(图 6)，坡长为65 m，坡度为30°，垂直坡面土层厚度H为6.5 m，地下水深度H_w为5.8 m。选取浙江省山地丘陵地区边坡常见残积土为上覆土体^[26]，算例中土体参数见表 1，土-水特征曲线和渗透系数曲线分别如图 7、8所示。通过计算，降雨导致的湿润层土体体积含水率θ_w为0.37，此时湿润层土体重度γ_t为19.5 kN/m³。

Fig. 6
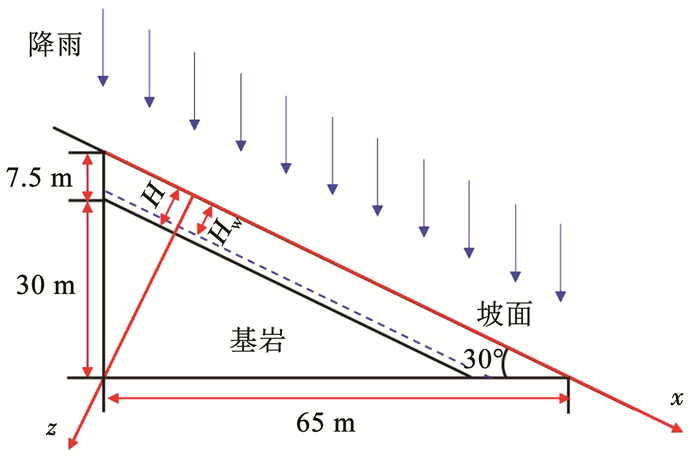图 6 均质浅层边坡分析示意 Fig. 6 Analysis diagram of homogeneous shallow slope


表 1
表 1 土体参数 Tab. 1 Soil parameters θ_sθ_rαs_f/cmk_s/(mm·h^-1)ρ_s/(g·cm^-3)γ_sat/(kN·m^-3)$ \frac{C}{V}$c′/kPaφ′/(°)φ^b/(°)

0.400.081.0211.7911.522.6919.800.4172826



表 1 土体参数 Tab. 1 Soil parameters


Fig. 7
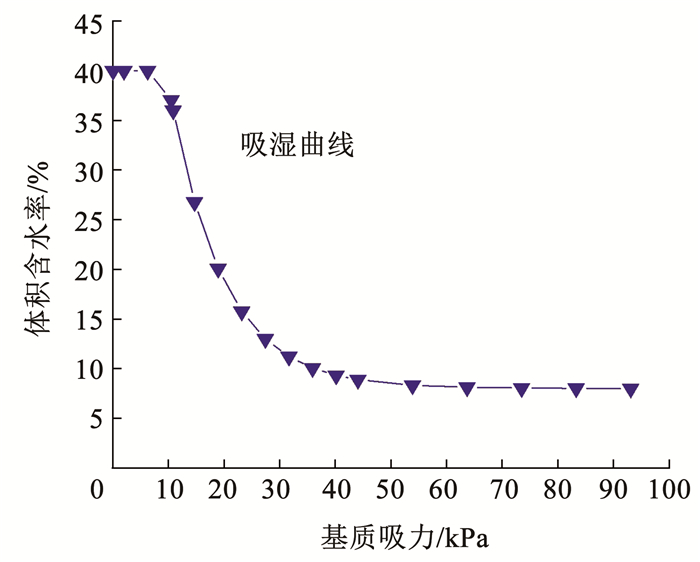图 7 土-水特征曲线 Fig. 7 Soil-water characteristic curve


Fig. 8
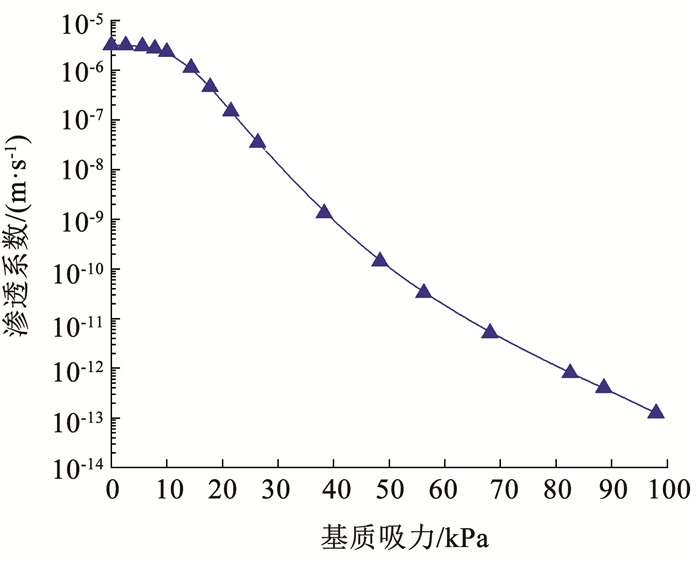图 8 渗透系数曲线 Fig. 8 Permeability coefficient curve


3.1 改进模型有效性验证 3.1.1 改进模型与传统模型计算结果对比当坡体含水率分布与Chen等^[10]假设(即初始含水率沿深度均匀分布)相同，改进模型可简化为

$t\left\{ \begin{array}{l}\frac{z_{\mathrm{w}}\left(\theta_{\mathrm{w}}-\theta_i\right)}{q \cos \beta}, 0 \leqslant t \leqslant t_{\mathrm{p}}\\t_{\mathrm{p}}+\frac{2\left(\theta_{\mathrm{w}}-\theta_i\right)\left(z_{\mathrm{w}}-z_{\mathrm{p}}\right)}{q \cos \beta+k_{\mathrm{s}}\left(\cos \beta+\frac{s_{\mathrm{f}}}{z_{\mathrm{w}}}\right)}, t>t_{\mathrm{p}}\end{array} \right.$ (34)

利用式(34)与Chen-Young模型^[10]分别计算当降雨强度为13 mm/h时(假定坡体初始体积含水率为0.18)湿润锋推移深度z_w与降雨时间t的关系，如图 9所示。可以看出，两者的湿润锋推移曲线比较接近，降雨持续60 h，两条曲线几乎重合，当湿润锋推移深度达到396 cm时，其相对最大误差小于3%，且改进模型计算结果偏于安全。可见，当假定初始含水率均匀分布时，改进模型与Chen-Young模型是等效的，改进模型是对传统模型在应用范围上的扩展。

Fig. 9
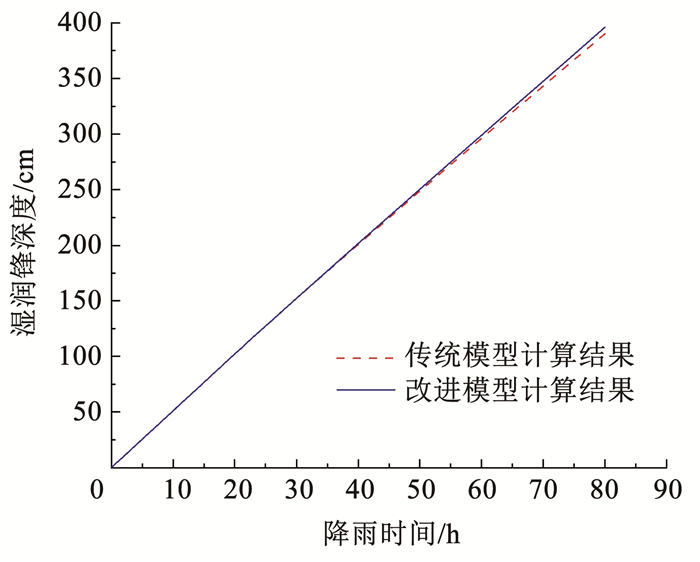图 9 含水率均匀分布时改进模型与传统模型计算结果对比 Fig. 9 Comparison between results of modified model and traditional model under uniform distribution of water content


3.1.2 改进模型与数值模拟计算结果对比采用SEEP/W数值模拟软件对浅层边坡存在初始地下水时的含水率分布及降雨入渗过程进行分析，以进一步验证改进模型的有效性。分析模型如图 10所示，其中，虚线为边坡初始地下水位线，其深度与图 6一致，并预先进行稳态渗流分析。

Fig. 10
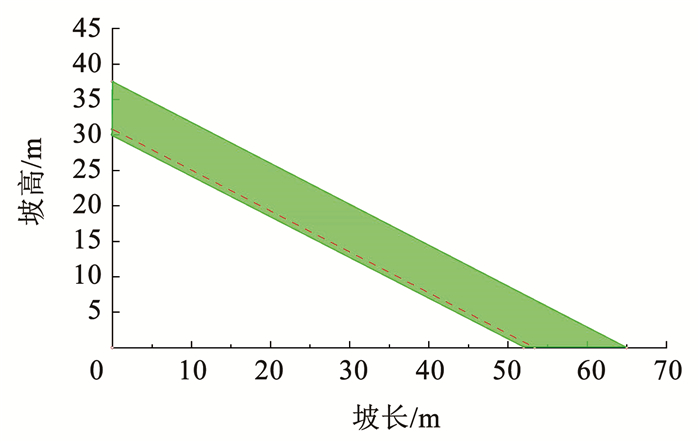图 10 数值模拟分析模型 Fig. 10 Analysis model for numerical simulation


首先利用式(3)对SEEP/W软件中稳态渗流分析获得的坡体体积含水率沿深度分布数据点进行拟合(图 11)，其中，拟合得到的参数θ_A为0.10，拟合优度达到0.96，可见采用式(3)描述存在初始地下水的浅层边坡土体体积含水率沿深度分布是可行的。

Fig. 11
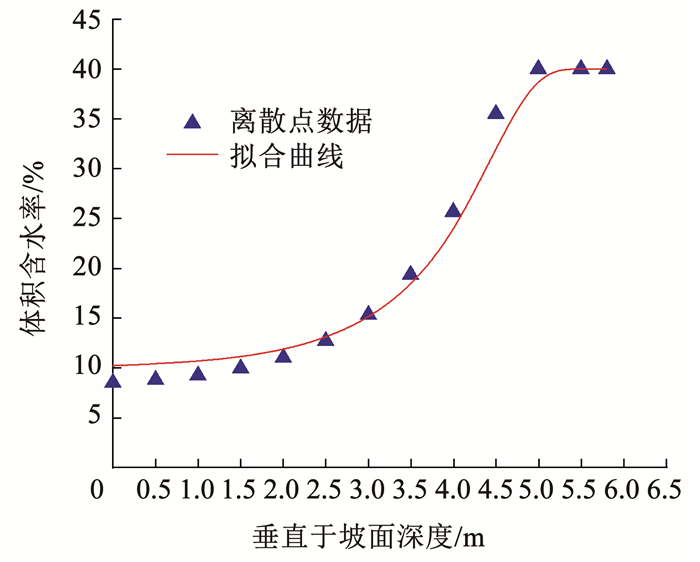图 11 坡体初始含水率沿深度分布曲线 Fig. 11 Distribution of initial volumetric water content of slope with depth


然后将雨强定义为流量边界进行降雨入渗过程分析，通过定义孔隙水压力值获得降雨时间t对应的湿润锋推移深度z_w ^[8]，并与本文改进模型结果进行比较。如图 12所示，两种方法计算得到的降雨强度为11 mm/h时湿润锋推移深度z_w与降雨时间t对应关系比较接近，但数值模拟得到的湿润锋推移深度要比改进模型结果稍大，在降雨持续95 h内最大偏差为12 cm，相对误差为2.71%，这是因为SEEP/W在降雨入渗分析时土体湿润层与初始层之间存在一个较窄的过渡段，该段即为两个模型计算结果的偏差。

Fig. 12
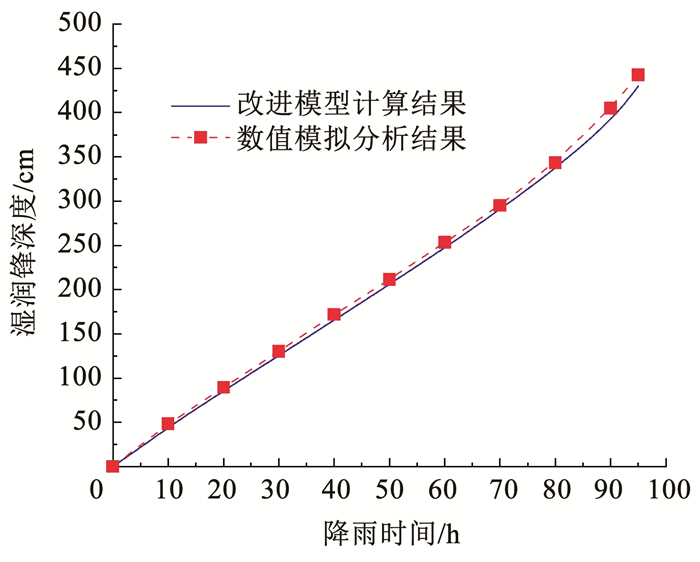图 12 改进模型与数值模拟分析结果对比 Fig. 12 Comparison between results of modified model and numerical simulation


3.2 降雨入渗过程分析 3.2.1 弱降雨工况(q≤k_s)采用改进模型(即考虑地下水影响时初始含水率指数分布)与Chen-Young模型(取改进模型坡面体积含水率0.10为初始均匀含水率值)分别计算降雨强度为5、7、9、11 mm/h时湿润锋推移深度与降雨时间的关系，结果如图 13所示。初始含水率均匀分布时，湿润锋推移速度随降雨强度增加而加快，且同一降雨强度在入渗过程中其推移速度保持不变；考虑地下水影响即初始含水率呈指数分布时，由于坡体初始含水率沿深度逐渐增大，单位深度土体达到近饱和状态时所需雨量逐渐减小，因此同一降雨强度在入渗过程中湿润锋推移速度逐渐加快。

Fig. 13
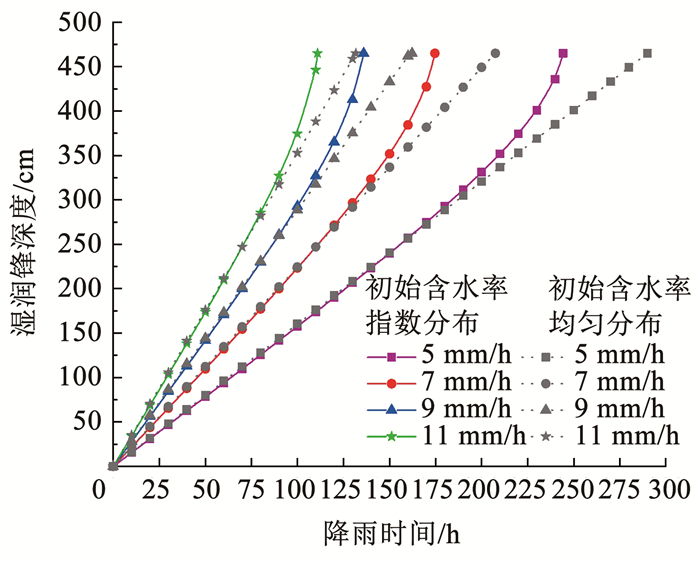图 13 弱降雨工况下降雨时间与湿润锋推移深度关系曲线 Fig. 13 Wetting front depth-rainfall duration curves under weak rainfall conditions


3.2.2 强降雨工况(q>k_s)采用改进模型与Chen-Young模型分别计算降雨强度为13、15、18、21 mm/h时，考虑地下水和不考虑地下水影响时(含水率分布与弱降雨工况相同)湿润锋推移深度与降雨时间的关系，结果如图 14所示。初始含水率均匀分布时，坡面产生径流的时间受降雨强度影响明显，坡面产流后不同降雨强度下，降雨时间达到130 h时对应的湿润锋推移深度最大差距仅为2.7 cm，此时，降雨入渗率受土体自身入渗能力控制；考虑地下水影响即初始含水率呈指数分布时，强降雨工况下增加降雨强度导致湿润锋推移速度虽仍有增加，但相比弱降雨工况增加速度变缓。同一降雨强度下湿润锋推移速度呈现先基本保持不变然后逐渐加快的趋势，此时，降雨入渗率受土体自身入渗能力和坡体初始含水率共同控制，在靠近毛细饱和带附近土体时，湿润锋推移速度达到最大。

Fig. 14
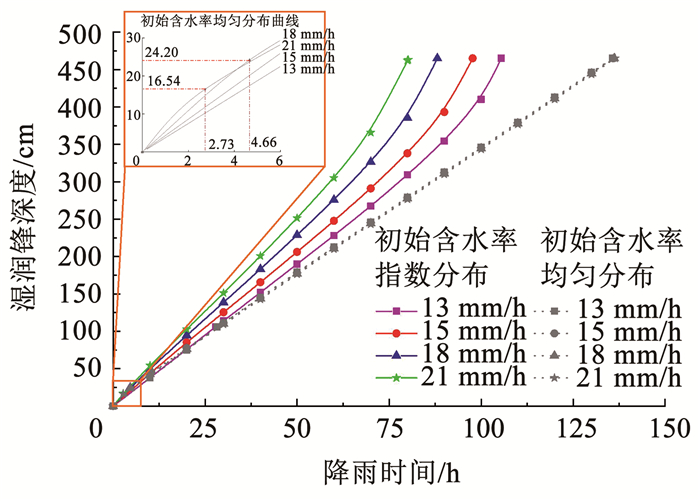图 14 强降雨工况下降雨时间与湿润锋推移深度关系曲线 Fig. 14 Wetting front depth-rainfall duration curves under heavy rainfall conditions


利用改进模型计算降雨强度为13、15、18、21、24、27 mm/h时对应的坡面产流临界时间t_p和对应的湿润锋推移深度z_p。如图 15所示，强降雨工况下提高降雨强度会明显缩短坡面产生径流的临界时间，此后一部分降雨将沿坡面流走。

Fig. 15
图 15 降雨强度与坡面产流临界时间/深度关系 Fig. 15 Timing of runoff on slope surface and wetting front depth under different rainfall intensities


3.3 考虑初始地下水影响的浅层边坡降雨作用下稳定性分析 3.3.1 坡体初始含水率分布对失稳时间和失稳位置的影响分别分析坡体在初始含水率均匀分布(假定初始体积含水率为0.18)和考虑地下水影响时初始含水率指数分布两种情况下降雨型浅层滑坡失稳时间和失稳位置，当降雨强度为7 mm/h时，浅层边坡湿润锋处和基岩面处的安全系数与降雨时间的关系分别如图 16和17所示。根据唐扬等^[27]的结论，当安全系数小于1.05时，边坡即将失稳，应进行滑坡灾害风险预警预报。

Fig. 16
图 16 初始含水率均匀分布时安全系数与降雨时间关系 Fig. 16 Factor of safety over rainfall duration with uniform distribution of initial volumetric water content


Fig. 17
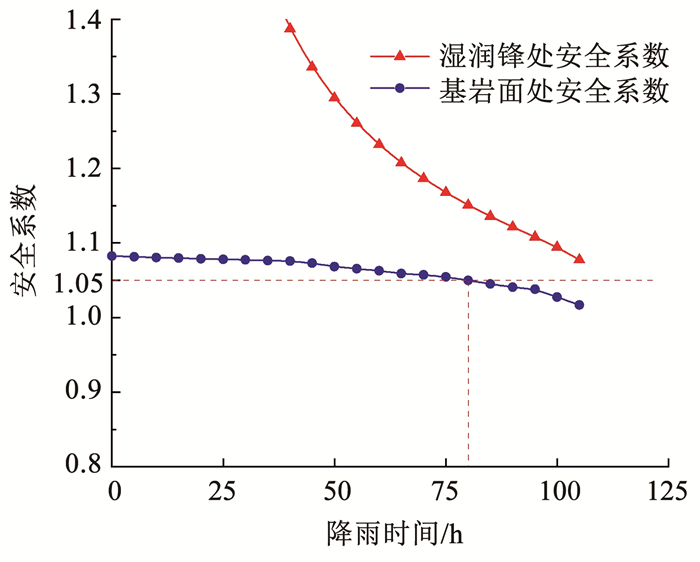图 17 考虑初始地下水影响的安全系数与降雨时间关系 Fig. 17 Factor of safety over rainfall duration considering initial groundwater


由图 16可知，当降雨时间达到115 h时，湿润锋处安全系数已减小至1.05，此时基岩面处的安全系数为1.14，说明该工况下将在湿润锋处发生失稳；当浅层边坡基岩处土层存在初始地下水时，如图 17所示，降雨时间达到77 h，基岩面处的安全系数降低至1.05，此时湿润锋处安全系数为1.15，说明该工况下失稳位置将发生在基岩面处，且基岩面处初始安全系数仅为1.08，即该类边坡在降雨前即处于欠稳定状态。

3.3.2 降雨强度对失稳时间和失稳位置的影响利用改进模型计算降雨强度为5、7、9、11、13、15、18、21、24、27 mm/h时存在初始地下水的浅层边坡失稳时间和失稳位置，结果如图 18所示。

Fig. 18
图 18 不同降雨强度下失稳时间和失稳位置关系 Fig. 18 Failure time and location of infinite slope under different rainfall intensities


由图 18可以看出，当降雨强度q小于k_s时，降雨强度从5 mm/h提高到11 mm/h，边坡触发失稳时间从108 h呈近指数关系快速缩短至45 h；当降雨强度q大于k_s时，降雨强度从15 mm/h增大到27 mm/h，失稳时间仅从42 h缩短到30 h，失稳时间缩短速度趋缓，此时大多降雨以径流的形式沿坡面流走，当不考虑坡面径流对入渗的促进作用时，影响边坡稳定性的降雨入渗量趋于稳定；当基岩面处土层存在稳定的初始地下水时，失稳位置往往发生在基岩面处而非传统预警预报模型中的湿润锋处，因此，重点关注该类边坡可以提高滑坡降雨阈值预测的准确性。

4 结论1) 浙江省山地丘陵地区浅层边坡土层通常存在稳定的初始地下水，本文基于土体非饱和特性，提出了边坡土体体积含水率指数分布模型，基于GA入渗模型及水量平衡原理推导了存在初始地下水的浅层边坡在弱降雨和强降雨两类工况下的入渗过程解析解。

2) 将改进模型与传统模型和数值模拟计算结果对比，验证了改进模型的有效性，将其应用于基岩处土层存在初始地下水的浅层边坡降雨入渗及稳定性分析，拓展了传统模型的应用范围，且解析解模型更有利于工程上的应用。

3) 当浅层边坡存在初始地下水时，边坡在降雨前即处于欠稳定状态，当降雨发生后，该类边坡失稳位置将发生在基岩面处，此时湿润锋处还偏于安全，且失稳时间提前于传统模型的预测结果，须重点关注。

4) 弱降雨工况下，降雨强度提高，边坡失稳启动时间呈近指数关系快速缩短；强降雨工况下，降雨强度提高，边坡失稳启动时间缩短速度趋缓，此时大多数降雨以径流的形式沿坡面流走，当不考虑坡面径流对入渗的促进作用时，影响边坡稳定的降雨入渗量趋于稳定。


参考文献
[1] 中华人民共和国国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2021: 8.
National Bureau of Statistics of the People's Republic of China. China statistical yearbook[M]. Beijing: China Statistics Press, 2021: 8.


[2] 麻土华, 孙乐玲, 李炜, 等. 浙江滑坡类型、成因和环境控制因素与影响因素[J]. 中国地质灾害与防治学报, 2010, 21(3): 17.
MA Tuhua, SUN Leling, LI Wei, et al. Landslide types and causal factors in Zhejiang region, China[J]. The Chinese Journal of Geological Hazard and Control, 2010, 21(3): 17. DOI:10.16031/j.cnki.issn.1003-8035.2010.03.016


[3] CHO S E. Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration[J]. Engineering Geology, 2017, 231: 126. DOI:10.1016/j.enggeo.2017.10.018


[4] SORBINO G, NICOTERA M V. Unsaturated soil mechanics in rainfall-induced flow landslides[J]. Engineering Geology, 2013, 165: 106. DOI:10.1016/j.enggeo.2012.10.008


[5] 连继峰, 罗强, 张文生, 等. 路堤边坡膨胀土强度非线性应力阈值与浅层稳定性[J]. 哈尔滨工业大学学报, 2021, 53(3): 143.
LIAN Jifeng, LUO Qiang, ZHANG Wensheng, et al. Nonlinear stress threshold for expansive soil strength and shallow stability of embankment slope[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 143. DOI:10.11918/201908149


[6] 王全九, 来剑斌, 李毅. Green-Ampt模型与Philip入渗模型的对比分析[J]. 农业工程学报, 2002, 18(2): 14.
WANG Quanjiu, LAI Jianbin, LI Yi. Comparison of Green-Ampt model with Philip infiltration model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2002, 18(2): 14.


[7] IVERSON R M. Landslide triggering by rain infiltration[J]. Water Resources Research, 2000, 36(7): 1903. DOI:10.1029/2000WR900090


[8] CUOMO S, DELLA SALA M. Rainfall-induced infiltration, runoff and failure in steep unsaturated shallow soil deposits[J]. Engineering Geology, 2013, 162: 124. DOI:10.1016/j.enggeo.2013.05.010


[9] GREEN W H, AMPT G A. Studies of soil physics, part 1: the flow of air and water through soils[J]. The Journal of Agricultural Science, 1911, 4(1): 7. DOI:10.1017/S0021859600001441


[10] CHEN Li, YOUNG M H. Green-Ampt infiltration model for sloping surfaces[J]. Water Resources Research, 2006, 42(7): 7. DOI:10.1029/2005wr004468


[11] GAVIN K, XUE Jianfeng. A simple method to analyze infiltration into unsaturated soil slopes[J]. Computers and Geotechnics, 2008, 35(2): 228. DOI:10.1016/j.compgeo.2007.04.002


[12] 李宁, 许建聪, 钦亚洲. 降雨诱发浅层滑坡稳定性的计算模型研究[J]. 岩土力学, 2012, 33(5): 1486.
LI Ning, XU Jiancong, QIN Yazhou. Research on calculation model for stability evaluation of rainfall-induced shallow landslides[J]. Rock and Soil Mechanics, 2012, 33(5): 1486. DOI:10.3969/j.issn.1000-7598.2012.05.033


[13] 马世国, 韩同春, 徐日庆. 强降雨和初始地下水对浅层边坡稳定的综合影响[J]. 中南大学学报(自然科学版), 2014, 45(3): 806.
MA Shiguo, HAN Tongchun, XU Riqing. Integrated effect of intense rainfall and initial groundwater on slope stability[J]. Journal of Central South University (Science and Technology), 2014, 45(3): 806.


[14] 张洁, 吕特, 薛建锋, 等. 适用于斜坡降雨入渗分析的修正Green-Ampt模型[J]. 岩土力学, 2016, 37(9): 2455.
ZHANG Jie, LV Te, XUE Jianfeng, et al. Modified Green-Ampt model for analyzing rainfall infiltration in slopes[J]. Rock and Soil Mechanics, 2016, 37(9): 2455. DOI:10.16285/j.rsm.2016.09.003


[15] 简文星, 蒋毅. 基于指数型的浅层滑坡非积水降雨入渗模型研究[J]. 安全与环境工程, 2017, 24(1): 24.
JIAN Wenxing, JIANG Yi. Exponential model of rainfall infiltration of shallow landslides for non-ponding conditions[J]. Safety and Environmental Engineering, 2017, 24(1): 24. DOI:10.13578/j.cnki.issn.1671-1556.2017.01.004


[16] BAUM R L, GODT J W, SAVAGE W Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration[J]. Journal of Geophysical Research, 2010, 115(F3): F3013. DOI:10.1029/2009jf001321


[17] GARDNER W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228. DOI:10.1097/00010694-195804000-00006


[18] SAVAGE W, GODT J, BAUM R. Modeling time-dependent areal slope stability[M]. London: A A Balkema, 2004: 166.


[19] WU Songbai, CHUI T F M, CHEN Li. Modeling slope rainfall-infiltration-runoff process with shallow water table during complex rainfall patterns[J]. Journal of Hydrology, 2021, 599: 126458. DOI:10.1016/j.jhydrol.2021.126458


[20] BEVEN K, ROBERT E. Horton's perceptual model of infiltration processes[J]. Hydrological Processes, 2004, 18(17): 3448. DOI:10.1002/hyp.5740


[21] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892. DOI:10.2136/sssaj1980.03615995004400050002x


[22] MEIN R G, FARRELL D A. Determination of wetting front suction in the Green-Ampt equation[J]. Soil Science Society of America Journal, 1974, 38(6): 873. DOI:10.2136/sssaj1974.03615995003800060014x


[23] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils[M]. New York: John Wiley & Sons, 1993: 88.


[24] VANAPALLI S K, FREDLUND D G, PUFAHL D E, et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal, 1996, 33: 384. DOI:10.1139/t96-060


[25] WANG Wei, ZHAO Yu, ZHANG Taili, et al. Regional soil thickness mapping based on stratified sampling of optimally selected covariates[J]. Geoderma, 2021, 400(3): 115092. DOI:10.1016/j.geoderma.2021.115092


[26] 郭俊英, 朱红雷. 浙江省小流域降雨型滑坡特点及机理研究[J]. 浙江水利科技, 2014, 42(3): 8.
GUO Junying, ZHU Honglei. Study on characteristics and mechanism of rainfall-induced landslides in small watersheds of Zhejiang province[J]. Zhejiang Hydrotechnics, 2014, 42(3): 8. DOI:10.13641/j.cnki.33-1162/tv.2014.03.003


[27] 唐扬, 殷坤龙, 夏辉. 前期含水率对浅层滑坡降雨入渗及稳定性影响研究[J]. 地质科技情报, 2017, 36(5): 207.
TANG Yang, YIN Kunlong, XIA Hui. Effects of initial water content on the rainfall infiltration and stability of shallow landslide[J]. Geological Science and Technology Information, 2017, 36(5): 207. DOI:10.19509/j.cnki.dzkq.2017.0527