刘征1,余志毅1,2,孙伟华1,张珂1
(1.北京理工大学 机械与车辆学院,北京 100081; 2.水沙科学与水利水电工程国家重点实验室(清华大学),北京 100084)
摘要:
为研究循环式冷却系中涉及的过冷沸腾流动传热特性,基于VOF多相流模型和Lee相变模型对一水平管道中的过冷流动沸腾过程进行非稳态数值计算。考虑到沸腾起始点的影响,在Lee模型的基础上引入Bergles提出的沸腾起始点关联式以对其进行修正。从热边界层发展和沸腾阶段的发展两方面分析水平管道过冷沸腾换热过程中的流动换热特性及其波动规律,总结了不同热流密度工况下相关参数的分布关系以及对流换热系数沿流动方向的分布规律。结果表明:热边界层的发展和沸腾不断加剧使得流场的不稳定性增加,加热区域后部对流换热系数的波动幅值是入口附近的2倍；热流密度的增加使得流动和换热参数沿流动方向的变化速度加快,热流密度为250 kW/m2工况下,热边界层发展所影响区域约为150 kW/m2工况下的60%；热边界层的发展使得加热段前部的对流换热系数呈现前高后低的特点。当受热区域热流密度较大时,换热设备可以通过减小换热通道长度的方式,在提升换热效率同时减小沸腾带来的换热系数波动的影响。
关键词: 传热 数值模拟 相变 过冷流动沸腾 非稳态
DOI：10.11918/202208069
分类号:TK124；O359
文献标识码:A
基金项目:北京市自然科学基金(3212021)；清华大学水沙科学与水利水电工程国家重点实验室开放基金(sklhse-2021-E-01)
Unsteady numerical calculation of subcooled boiling heat transfer in a horizontal pipe
LIU Zheng1,YU Zhiyi1,2,SUN Weihua1,ZHANG Ke1
(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.State Key Laboratory of Hydroscience and Engineering (Tsinghua University), Beijing 100084, China)
Abstract:
In order to study the characteristics of heat transfer in subcooled flow boiling of circulating cooling system, the unsteady numerical calculation of the subcooled flow boiling process of a horizontal pipe was carried out based on the VOF multiphase model and the Lee phase change model. The correlation of boiling onset proposed by Bergles was introduced for correcting the Lee model, taking into account the influence of the boiling onset. The heat transfer properties of the subcooled flow boiling process in the horizontal pipe and their variation rules were examined from two aspects: the thermal boundary layer development and the boiling development. The distribution regularity of relevant parameters under different heat flux conditions was summarized, as well as the distribution rules of heat transfer coefficient along the flow direction. Results showed that the development of the thermal boundary layer and boiling would enhance the instability of the flow field, and the fluctuation amplitude of the heat transfer coefficient in the rear was twice as large as in the front. Moreover, the increase of the heat flux accelerated the variation of the flow and heat transfer parameters along the flow direction. In the 250 kW/m2 condition, the area affected by the thermal boundary development was about 60% that of the 150 kW/m2 condition. The heat transfer coefficient in the front of the heating section showed a descending trend with the development of the thermal boundary layer. Therefore, when the heating area is in high flux condition, we can shorten the length of the heat exchanger to increase the heat exchange efficiency and weaken the fluctuation of the heat transfer coefficient caused by flow boiling.
Key words: heat transfer numerical simulation phase change subcooled flow boiling unsteady state
刘征, 余志毅, 孙伟华, 张珂. 水平管道过冷沸腾换热的非稳态数值计算[J]. 哈尔滨工业大学学报, 2023, 55(6): 39-45. DOI: 10.11918/202208069.
LIU Zheng, YU Zhiyi, SUN Weihua, ZHANG Ke. Unsteady numerical calculation of subcooled boiling heat transfer in a horizontal pipe[J]. Journal of Harbin Institute of Technology, 2023, 55(6): 39-45. DOI: 10.11918/202208069.
基金项目 北京市自然科学基金(3212021);清华大学水沙科学与水利水电工程国家重点实验室开放基金(sklhse-2021-E-01) 作者简介 刘征(1995—)，男，硕士研究生;
余志毅(1976—)，男，副教授，博士生导师 通信作者 余志毅, yuzhiyi@bit.edu.cn 文章历史 收稿日期: 2022-08-17
Abstract Full text Figures/Tables PDF
水平管道过冷沸腾换热的非稳态数值计算
刘征1, 余志毅1,2
, 孙伟华1, 张珂1 1. 北京理工大学 机械与车辆学院，北京 100081;
2. 水沙科学与水利水电工程国家重点实验室(清华大学)，北京 100084
收稿日期: 2022-08-17; 录用日期: 2022-10-24; 网络首发日期: 2022-11-09
基金项目: 北京市自然科学基金(3212021);清华大学水沙科学与水利水电工程国家重点实验室开放基金(sklhse-2021-E-01)
作者简介: 刘征(1995—)，男，硕士研究生; 余志毅(1976—)，男，副教授，博士生导师
通信作者: 余志毅, yuzhiyi@bit.edu.cn
摘要: 为研究循环式冷却系中涉及的过冷沸腾流动传热特性，基于VOF多相流模型和Lee相变模型对一水平管道中的过冷流动沸腾过程进行非稳态数值计算。考虑到沸腾起始点的影响，在Lee模型的基础上引入Bergles提出的沸腾起始点关联式以对其进行修正。从热边界层发展和沸腾阶段的发展两方面分析水平管道过冷沸腾换热过程中的流动换热特性及其波动规律，总结了不同热流密度工况下相关参数的分布关系以及对流换热系数沿流动方向的分布规律。结果表明：热边界层的发展和沸腾不断加剧使得流场的不稳定性增加，加热区域后部对流换热系数的波动幅值是入口附近的2倍；热流密度的增加使得流动和换热参数沿流动方向的变化速度加快，热流密度为250 kW/m2工况下，热边界层发展所影响区域约为150 kW/m2工况下的60%；热边界层的发展使得加热段前部的对流换热系数呈现前高后低的特点。当受热区域热流密度较大时，换热设备可以通过减小换热通道长度的方式，在提升换热效率同时减小沸腾带来的换热系数波动的影响。
关键词: 传热 数值模拟 相变 过冷流动沸腾 非稳态
Unsteady numerical calculation of subcooled boiling heat transfer in a horizontal pipe
LIU Zheng1, YU Zhiyi1,2
, SUN Weihua1, ZHANG Ke1 1. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;
2. State Key Laboratory of Hydroscience and Engineering (Tsinghua University), Beijing 100084, China
Abstract: In order to study the characteristics of heat transfer in subcooled flow boiling of circulating cooling system, the unsteady numerical calculation of the subcooled flow boiling process of a horizontal pipe was carried out based on the VOF multiphase model and the Lee phase change model. The correlation of boiling onset proposed by Bergles was introduced for correcting the Lee model, taking into account the influence of the boiling onset. The heat transfer properties of the subcooled flow boiling process in the horizontal pipe and their variation rules were examined from two aspects: the thermal boundary layer development and the boiling development. The distribution regularity of relevant parameters under different heat flux conditions was summarized, as well as the distribution rules of heat transfer coefficient along the flow direction. Results showed that the development of the thermal boundary layer and boiling would enhance the instability of the flow field, and the fluctuation amplitude of the heat transfer coefficient in the rear was twice as large as in the front. Moreover, the increase of the heat flux accelerated the variation of the flow and heat transfer parameters along the flow direction. In the 250 kW/m2 condition, the area affected by the thermal boundary development was about 60% that of the 150 kW/m2 condition. The heat transfer coefficient in the front of the heating section showed a descending trend with the development of the thermal boundary layer. Therefore, when the heating area is in high flux condition, we can shorten the length of the heat exchanger to increase the heat exchange efficiency and weaken the fluctuation of the heat transfer coefficient caused by flow boiling.
Keywords: heat transfer numerical simulation phase change subcooled flow boiling unsteady state
过冷沸腾是指壁面温度高于饱和温度，液体主体温度低于饱和温度下所发生的局部沸腾现象，作为一种强化换热方式应用于内燃机、电子元器件、充电电缆、车用电池以及大功率激光武器等重要设备的散热[1-7]。有学者针对过冷沸腾流动换热进行了大量数值计算方面的研究，可以分为两方面：一类是稳态计算，这类计算的计算量较小，一般针对相对复杂的结构，只能获取各参数的结果分布[5-10]；另一类是同时反映参数分布规律和瞬时特性非稳态计算，侧重于对流动过程参数的获取，计算量较大，更能接近实际沸腾过程。魏敬华等[11]对竖直窄缝通道内的过冷流动沸腾进行了数值计算研究，分析了不同压力和热流密度下的汽泡动力学特性；潘良明等[12]建立了过冷流动沸腾凝结模型，以分析汽泡凝结过程的流场特性；葛苏槿[13]从含气率、物理场、汽泡行为等方面对一倾斜管道内过冷沸腾换热特性进行了数值研究；Lee等[14-17]针对垂直管道内FC-72的过冷沸腾进行了大量研究，首先研究了上升流中的高过冷度核态沸腾，总结了换热系数沿轴向的变化规律，提出了一种适用于VOF模型的剪切力计算方法，并研究了高过冷度沸腾在CHF点前后的流动传热特性以及微重力条件下的低过冷度沸腾中的汽泡行为和流型演化；Yeo等[18]在不涉及蒸干的情况下成功模拟了微通道中的过冷沸腾，通过与实验以及经验关联式验证了数值计算方法的有效性；Chen等[19]对矩形微通道的过冷沸腾进行了数值模拟，分析了含气率和热流密度对换热的影响；曹涛涛[20]基于水平通道中的过冷沸腾，提出了确定Lee模型中传质系数的经验关联式。
现有研究中针对过冷沸腾换热过程换热参数波动和分布规律方面的研究较少，实际上换热参数的波动和分布是气液相变换热设备设计的重要依据，参数波动过大产生的热应力会降低换热设备的可靠性，而换热参数的分布规律是确定换热设备几何尺寸的重要参考。基于此，针对一宏观尺度中小直径水平管道内的过冷沸腾换热过程进行非稳态数值计算，分析沸腾过程中流动和换热参数的分布及波动特性，并对过冷沸腾换热的规律进行总结，为新型换热设备的相关设计提供借鉴经验。
1 物理模型及网格划分参考目前应用广泛的换热设备(如闭式冷却系统中的冷却水套以及板翅式换热器)的通道高度，利用ICEM_CFD 2020 R2建立了一个高度为10 mm的水平管道二维模型，如图 1所示。管道总长为800 mm，其中入口段200 mm，加热段100 mm，出口段500 mm。采用下壁面加热方式，底部加热面与流固耦合面之间的固体域厚度为0.5 mm。
Fig. 1
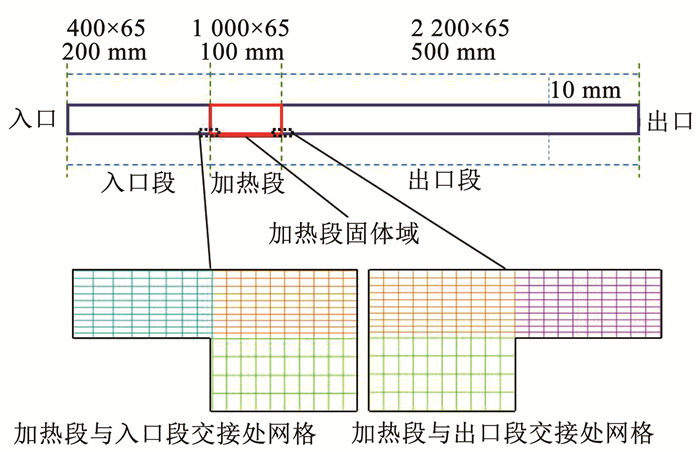图 1 物理模型及计算域网格分布 Fig. 1 Physical modeland mesh distribution in the computational domain 通过ICEM_CFD软件对计算域划分4套网格，网格总数分别为65 950、107 250、225 000、274 000。选择基准工况，以加热壁面固体域的平均温度作为检验标准。计算发现，当网格总数在225 000以上时，加热壁面固体域的平均温度变化幅度已经很小。综合考虑计算量与计算精度，最终选择第3套网格，即总数为225 000的网格，其中, 流体域纵向网格数为65，横向网格数为3 600，对加热段、出口延伸段前部以及壁面附近的网格进行加密，第1层网格高度为0.05 mm，Y Plus值为3.78。
2 计算模型及设置 2.1 计算模型的选取VOF多相流模型是一种针对两种或两种以上流体的界面跟踪技术，其优势是能够清晰地捕捉到两相之间的交界面。为了更准确地捕捉汽泡的生成发展过程，分析汽泡的运动规律，选择VOF模型对过冷沸腾换热过程进行计算。
湍流模型选择SST k-ω模型，湍流阻力因子设置为10，以对壁面处的汽泡生成发展的非稳态过程进行更好的描述[21]。
此外，相变模型是过冷沸腾数值计算所涉及的重要模型。由Lee在1980年提出的半隐式传热传质模型——Lee模型[22]，是目前应用最为广泛的相变模型。该模型将相变过程简化为饱和温度与实际温度的温差驱动的传质过程，其形式简单且能够模拟沸腾和凝结过程的全阶段，Lee模型的基本方程如下[21-22]：
连续方程为
$\frac{\partial}{\partial t}\left(\alpha_v \rho_{\mathrm{v}}\right)+\nabla \cdot\left(\alpha_{\mathrm{v}} \rho_{\mathrm{v}} \boldsymbol{v}_{\mathrm{v}}\right)=m$ (1)
Lee模型相变过程质量传递源项求解方式为
$m=\left\{\begin{array}{l}r_{\mathrm{e}} \alpha_1 \rho_1 \frac{\left(T-T_{\text {sat }}\right)}{T_{\text {sat }}}, T \geqslant T_{\text {sat }} \\r_{\mathrm{c}} \alpha_{\mathrm{v}} \rho_{\mathrm{v}} \frac{\left(T_{\text {sat }}-T\right)}{T_{\text {sat }}}, T<T_{\text {sat }}\end{array}\right.$ (2)
能量传递源项为质量源项与汽化潜热的乘积，表示为
$Q=m h_{\mathrm{fg}}$ (3)
式中：α为相体积分数；ρ为密度，kg/m3；v为速度矢量；Q为能量传递源项，J/(s · m3)；m为质量传递源项，kg/(s · m3)；hfg为汽化潜热，J/kg；T为流体温度，K；Tsat为饱和温度，K；r为相变传质系数，s-1，其取值需要根据具体工况进行调整，本研究所采取的方式为结合计算关联式的结果对传质系数的取值进行若干次试算，最终在3种不同热流密度(150、200、250 kW/m2)下，汽化传质系数分别确定为0.1、0.5、2.0。鉴于气相密度较低，一般认为凝结传质系数应当取较大值，Kim等[23]认为凝结传质系数应当在汽化传质系数的基础上乘以液体密度与气体密度的比值，以此为基础，近似将汽化传质系数与凝结传质系数的比确定为1/1 600，故凝结传质系数的取值分别为160、800、3 200；下标v和l分别代表气相和液相，下标e和c分别代表汽化和凝结过程。
此外，基于核沸腾起始需要一定的过热条件，通过UDF功能将Bergles提出的沸腾起始点计算关联式[24]嵌入由Lee模型构建的传热传质源项表达式中，计算沸腾起始阶段所需过热度，作为计算沸腾核化前单相液体换热的补充，计算关联式为
$T_{\mathrm{ONB}}-T_{\mathrm{sat}}=\frac{5}{9}\left[\frac{q_{\mathrm{ONB}}}{1082\left(p / 10^5\right)^{1.156}}\right]^{\frac{(p / 10^5)^{0.0234}}{2.16}}$ (4)
式中：p为绝对压力，Pa；qONB为沸腾起始点热流密度，W/m2；TONB为该热流密度下所对应的沸腾起始点温度，K；TONB-Tsat即所在位置达到沸腾起始点所需过热度，沸腾起始点温度通过所在位置相邻接触面的局部热流密度以及所在位置的局部压力求得。
基于此，将成核位置限制在靠近加热面的近壁区，当流体存在一定过热，但局部区域不存在相界面时，认为该区域处于沸腾核化前的单相阶段，由于此时将要发生的汽化过程位于液相内部，近似以沸腾起始点温度作为此时的汽化温度，将式(2)的质量传递源项修正为
$m=\left\{\begin{array}{l}r_{\mathrm{e}} \alpha_1 \rho_1 \frac{\left(T-T_{\mathrm{sat}}\right)}{T_{\mathrm{sat}}}, T \geqslant T_{\mathrm{ONB}} \\0, T<T_{\mathrm{ONB}}\end{array}\right.$ (5)
当沸腾过程存在相界面或发生气相的凝结过程时，质量源项求解仍使用式(2)。最后，通过Fluent中的UDF功能，将当前质量源项的求解结果引入计算。综合考虑式(4)和(5)，质量源项可以表达为
$m=\left\{\begin{array}{l}r_{\mathrm{e}} \alpha_1 \rho_1 \frac{\left(T-T_{\text {sat }}\right)}{T_{\text {sat }}}, T \geqslant T_{\text {sat }} \, \& \, \alpha \neq 0 \\r_{\mathrm{e}} \alpha_1 \rho_1 \frac{\left(T-T_{\text {sat }}\right)}{T_{\text {sat }}}, T \geqslant T_{\mathrm{ONB}} \, \& \, \alpha=0 \\0, T_{\text {sat }} \leqslant T<T_{\mathrm{ONB}} \, \& \, \alpha=0 \\r_{\mathrm{c}} \alpha_{\mathrm{v}} \rho_{\mathrm{v}} \frac{\left(T_{\text {sat }}-T\right)}{T_{\text {sat }}}, T<T_{\text {sat }}\end{array}\right.$ (6)
2.2 边界条件和其他设置边界条件方面，入口边界流速为0.4 m/s，过冷度为5 K；出口压力设置为常压101 325 Pa；加热壁面设置3种热流密度，分别为150、200、250 kW/m2；表面张力的求解采用Brackbill等提出的CSF表面张力模型[25]。
压力速度的耦合采用SIMPLEC算法。对于标量方程各项的空间离散，压力采用PRESTO!格式，体积分数采用几何重构格式，能量和动量采用二阶迎风格式，湍动能和湍流耗散率采用一阶迎风格式；为保证计算的收敛性，采用可变时间步长，范围为5×10-6~5×10-4 s，限制全局库朗数为1以下，每个时间步的最大迭代次数设置为50，计算总时长设置为1.2 s。
3 计算结果分析 3.1 结果合理性验证数值计算结果的可靠性通过过冷流动沸腾换热经验关联式验证。常用的沸腾换热关联式中适用于过冷沸腾的关联式包括Chen关联式、Moles-Shaw关联式、Shah关联式的修正形式、Gungor-Winterton关联式以及Liu-Winterton关联式等。Chen[26]关联式作为最早的叠加关联式，将流动沸腾换热看作是液相强制对流换热和核态沸腾换热两种机制共同作用，通过两种机制的线性叠加求解流动沸腾过程的对流换热系数。此后在Chen关联式的基础上衍生出若干更为精确的沸腾传热关联式，如Gungor-Winterton关联式、Liu-Winterton关联式等。Gungor-Winterton[27]关联式在Chen关联式基础上针对核态沸腾换热过程的对流换热系数求解采用了更精确的Cooper[28]关联式，针对过冷沸腾考虑了核态沸腾换热和强制对流换热驱动温差不同做出改进，提升了求解精度；Liu-Winterton[29]关联式与Gungor-Winterton关联式类似，区别为Liu-Winterton关联式采用了非线性叠加方式。适用范围方面，Shah[30]过冷沸腾关联式的验证数据多数集中在普朗特数1以下，雷诺数10 000以上；而Gungor-Winterton关联式与Liu-Winterton关联式采用了相同的数据库，适用于雷诺数为568.9~875 000、普朗特数0.83~9.1的工况范围[29]，可覆盖本文数值计算的工况范围。基于以上，选择了Gungor-Winterton关联式对数值计算进行验证，其计算过冷沸腾对流换热系数的表达式如下：
$q=h_1\left(T_{\mathrm{w}}-T_{\mathrm{b}}\right)+S h_{\mathrm{pool}}\left(T_{\mathrm{w}}-T_{\mathrm{sat}}\right)$ (7)
$h_1=0.023\left(k_1 / d\right) {Re}_1^{0.8} {Pr}_1^{0.4}$ (8)
$h_{\text {pool }}=55 p_{\mathrm{r}}^{0.12} q^{2 / 3}\left(-\lg p_{\mathrm{r}}\right)^{-0.55} M^{-0.5}$ (9)
$S=\left(1+0.055 F^{0.1} R e_1^{0.16}\right)^{-1}$ (10)
$F=1+24000 B o^{1.16}$ (11)
$B o=\frac{q}{h_{\mathrm{fg}} G}$ (12)
式中：q为热流密度，W/m2；hl为单相对流换热系数，W/(m2 · K)；hpool为沸腾换热系数，W/(m2 · K)；F为对流换热强化因子，过冷沸腾不考虑该系数，取值为1；S为沸腾抑制因子; kl为液体热导率，W/(m · K)；d为水力直径，m；Rel为液相雷诺数；Prl为液相普朗特数；Bo为沸腾数；G为质量流速，kg/(m2 · s)；pr为对比压力；M为相对分子质量。
3种热流密度条件下，数值计算与实验关联式计算结果对比如表 1所示。可以看出，尽管存在一定偏差，但数值计算与关联式计算结果具有相同的趋势，认为当前所计算结果是合理的。
表 1
表 1 数值计算与Gungor-Winterton关联式计算结果对比 Tab. 1 Comparison between results from numerical calculation and Gungor-Winterton correlation 热流密度/(kW·m-2) 壁面过热度(数值计算)/K 壁面过热度(关联式)/K 相对误差/% 150 11.11 10.00 11.09
200 12.41 11.86 4.61
250 13.43 13.41 0.18
表 1 数值计算与Gungor-Winterton关联式计算结果对比 Tab. 1 Comparison between results from numerical calculation and Gungor-Winterton correlation
3.2 过冷沸腾流场的演变与换热特性波动以热流密度q为250 kW/m2的工况为例，流场在计算时间t为0.5 s时刻后到达相对稳定状态。图 2为该工况下0.7~1.2 s过冷沸腾流场中气相分布的变化及局部区域矢量图。可以看出，由于下壁面的加热，汽泡不断形成并随主流向下游运动。总体上看，加热段的前半部分汽泡较细、较少，处于核化、脱离和初步生长阶段，而后半部分汽泡明显增大，气泡的合并和消亡现象更明显。伴随着汽泡的核化、生长、脱离、消亡等过程，壁面与流体间的换热受到干扰。如图 2所示，由0.9和1.2 s时刻壁面附近的局部流场图可见，汽泡的生长和运动等行为对壁面附近流动造成强烈的扰动，并形成明显的漩涡。这些扰动使得管道换热面的换热性能得到强化的同时，将造成换热特性的波动。
Fig. 2
图 2 热流密度250 kW/m2工况加热段气相分布随时间t的变化及部分局部放大区矢量图 Fig. 2 Variation of gas phase distribution in heating section with time t under heat flux condition 250 kW/m2 and some local enlarged vector maps 图 3为与图 2相对应的温度分布。可以看出，从加热段进口到加热段约中间位置，热边界层沿流动方向逐渐增厚，此后该厚度无明显增加，在一均值上下波动。基于此特点，可将管内流动沸腾分为热边界层发展段与核沸腾主导段，250 kW/m2工况下两者的分界线约在横坐标X等于250 mm处。
Fig. 3
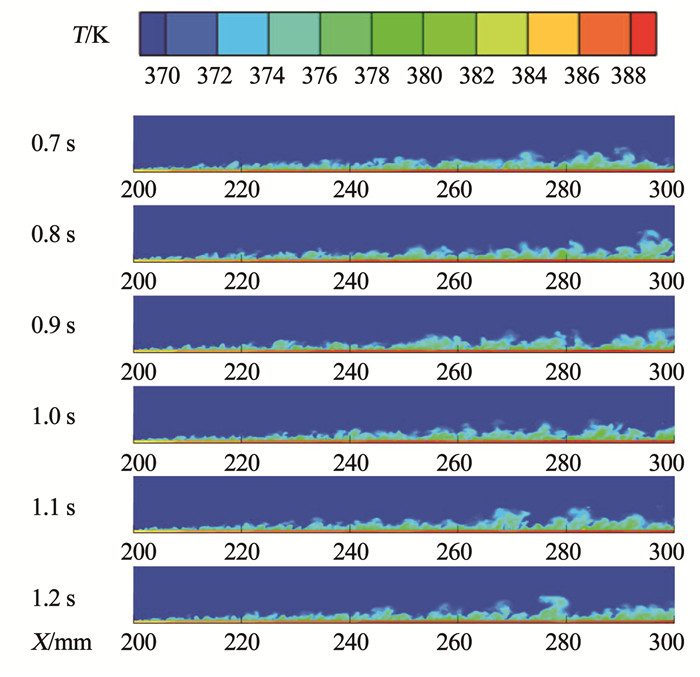图 3 热流密度250 kW/m2工况加热段温度分布随时间t的变化 Fig. 3 Variation of temperature distribution in heating section with time t under heat flux condition 250 kW/m2 在热边界层发展段，加热表面放出的热量部分用于加热壁面附近流体，使得该区域流体的温度逐渐升高，另一部分则通过液体的汽化过程被吸收；当热边界层温度达到饱和温度，边界层内热传递逐渐趋向稳定，进入核沸腾主导段，此时，主流区的温升以及汽化过程使得壁面附近流体温度随位置变化相对较小，壁面所放出的热量主要通过汽化过程被吸收。同时，对比图 2和3可知，核沸腾主导段的流场随时间的波动更为剧烈，表明沸腾过程增加了流场中的不稳定性。
图 4分别为加热区域各部分对流换热系数随时间的波动，每个样本点为0.05 s时间段内该区域的平均值。对比发现，各段对流换热系数随时间均存在波动性，热边界层发展段前部的换热系数波动幅值较小，而其下游区域换热系数波动幅值沿流动方向整体呈现增加趋势。造成前者波动趋势的原因是热边界层发展段前部的壁面温度与近壁面液相温度较低，显热带走了较多的热量，受到汽泡核化以及生长脱离过程影响较小，换热系数波动不明显，另一方面该段壁温相对较低，汽泡脱离直径较小，使得汽泡生长产生热阻所造成的影响更小，该段各部分的对流换热系数平均波动幅值小于核沸腾主导段；而下游区域近壁区温度升高造成壁面换热特性受汽泡生长脱离周期的影响明显，对流换热系数产生明显波动，受到汽泡脱离直径增加的影响，波动幅值整体较大。如200~220 mm段在0.5 s记录时间段内的波动幅值为414.16 W/(m2 · K)，而>260~280 mm段以及>280~300 mm段的波动幅值分别为1 196.33和815.93 W/(m2 · K)，>220~300 mm整体平均波动幅值为794.14 W/(m2 · K)，约为热边界层发展段前部波动幅值的2倍，且波动规律相似，表明汽泡的生长运动加剧了对流换热系数的波动，使得入口区域以外的波动规律具有相似特性。
Fig. 4
图 4 热流密度250 kW/m2工况下各部分对流换热系数h随时间t的变化 Fig. 4 Variation of heat transfer coefficient h of each part with time t under heat flux condition 250 kW/m2 3.3 热流密度对过冷沸腾流场的影响图 5~7分别为t为1.0 s时刻3个工况下的温度分布、气相分布以及速度分布，三者之间相互影响。如图 5所示，加热段热流密度的变化直接影响加热段近壁区温度分布，不同热流密度下，壁面附近液体温度升高速度不同，沸腾发生的位置和强度相应不同，对管内速度场产生不同影响。如图 6所示，随着热流密度增加，壁面附近出现明显汽泡的位置提前。q为150 kW/m2工况下壁面附近存在的汽泡数量很少，汽泡的生长、合并与脱离现象很不明显；与之相对，q为250 kW/m2的工况下汽泡活动范围得以扩大，其在加热段前部即产生细泡状流型，而后由于壁面温度的升高以及汽泡的生长合并使得其直径不断增大。同时，各工况下产生的汽泡对近壁区域流场产生不同程度的扰动，汽化过程造成的膨胀使得下游流速不同程度的升高，如图 7所示，热流密度越大，产生的汽泡越多，近壁区域流场速度分布越不规则，下游速度越大，其中，流体速度用v表示。
Fig. 5
图 5 各工况加热段温度分布 Fig. 5 Temperature distributionin heating section under different working conditions Fig. 6
图 6 各工况加热段气相分布 Fig. 6 Gas distribution in heating section under different working conditions Fig. 7
图 7 各工况加热段速度分布 Fig. 7 Velocity distribution in heating section under different working conditions 3.4 过冷沸腾对流换热系数随位置的变化由于当前工况水平管道的过冷沸腾是从单相逐渐转变为两相，加热面的对流换热系数随流动位置变化，不同工况下对流换热系数随位置的变化存在一定差异。
图 8为3个工况下，局部平均对流换热系数随位置的变化。与换热的波动特性类似，造成各局部平均换热系数变化的原因同样包含热边界层沿流动方向的发展以及沸腾对传热的强化两种机制。
Fig. 8
图 8 0.7~1.2 s对流换热系数h沿水平坐标X的变化 Fig. 8 Variation of heat transfer coefficient h along horizontal coordinate X in 0.7-1.2 s 对比图 5可以看出，热边界层发展段对流换热系数沿流动方向不断下降，热流密度越大，该区域对流换热系数沿流动方向变化越快，发展所需通道的长度越短，如图 8所示，150 kW/m2工况下该段长度为80 mm，200 kW/m2工况下为60 mm，250 kW/m2工况下为50 mm。这是由于热边界层处于发展阶段时，发展初期的热边界层很薄，近壁区液体温度较低且与主流区温度相近，由于温度场的连续性，壁面温度较低且与主流区的温差较小，单相导热及对流换热强度较高，随着壁面对附近流体的加热，近壁区域热边界层增厚，热阻相应变大，换热系数下降。热流密度越大，近壁区域的局部过热层产生越快，因此，热边界层发展所需的通道长度越短。
随着热边界层发展到一定程度，近壁区域的过热层内部发生沸腾，流场中开始出现明显的汽泡，沸腾对传热的强化作用不断增强，对流换热系数由逐渐下降转变为趋于稳定，进入核沸腾主导段。由于汽泡在各段的生长阶段不同，进入核沸腾主导段后对流换热系数随位置的变化存在一定小范围浮动，表明该阶段热边界层发展对传热的抑制减缓，核沸腾对换热的强化作用增强。
4 结论1) 短通道内过冷沸腾流场的演变及换热特性波动受热边界层发展和沸腾两种机制的影响，据此可将短通道加热区域分为热边界层发展段和核沸腾主导段。热边界层发展段的前部换热系数波动幅度较小，原因是入口附近的近壁区温度较低，受沸腾过程影响较小；热边界层发展段后部及核沸腾主导段在壁面附近形成过热液体层，受沸腾影响较大，换热系数的波动幅度增大。
2) 热流密度可促进水平管内流动参数和换热参数沿流动方向的变化。一方面，热流密度增加，近壁区温度、平均含气率及流动速度沿流动方向的提升越快，沸腾越剧烈；另一方面，热流密度的增加使得对流换热系数随热边界层发展达到相对稳定所需的距离越短。
综上，针对高热流密度工况下的过冷流动沸腾换热，可以采取适当减小通道长度的方式，以获得相对更大的对流换热系数，同时减小沸腾引起的流场参数波动和不稳定性。
参考文献
[1] 季爱林, 钟剑锋, 帅立国. 大热流密度电子设备的散热方法[J]. 电子机械工程, 2013, 6(6): 30.
JI Ailin, ZHONG Jianfeng, SHUAI Liguo. Cooling measures of high flux electronic equipment[J]. Electro-Mechanical Engineering, 2013, 6(6): 30. DOI:10.3969/j.issn.1008-5300.2013.06.007
[2] DEVAHDHANUSH V S, LEE S, MUDAWAR I. Consolidated theoretical/empirical predictive method for subcooled flow boiling in annuli with reference to thermal management of ultra-fast electric vehicle charging cables[J]. International Journal of Heat and Mass Transfer, 2021, 175(10): 121224. DOI:10.1016/j.ijheatmasstransfer.2021.121224
[3] WANG Yanfeng, WU Jiangtao. Thermal performance predictions for an HFE-7000 direct flow boiling cooled battery thermal management system for electric vehicles[J]. Energy Conversion and Management, 2020, 207: 112569. DOI:10.1016/j.enconman.2020.112569
[4] 周乐平, 唐大伟, 杜小泽, 等. 大功率激光武器及其冷却系统[J]. 激光与光电子学进展, 2007, 44(8): 34.
ZHOU Leping, TANG Dawei, DU Xiaoze, et al. High power laser weapons and their cooling systems[J]. Laser and Optoelectronics Progress, 2007, 44(8): 34.
[5] 张得志. 发动机冷却水套过冷沸腾数值分析[D]. 长春: 吉林大学, 2012
ZHANG Dezhi. The numerical analysis of subcooled boiling in engine water jacket[D]. Changchun: Jilin University, 2012
[6] 王冠雄. 汽油机水套内过冷沸腾传热的影响因素分析及模拟计算[D]. 长春: 吉林大学, 2013
WANG Guanxiong. Analysis of influence factor and numerical simulation of subcooled nucleate boiling heat transfer in gasoline engine water jacket[D]. Changchun: Jilin University, 2013
[7] 董非, 郭晨海, 范秦寅, 等. 发动机冷却水腔内沸腾换热的模拟研究[J]. 内燃机工程, 2011, 32(4): 76.
DONG Fei, GUO Chenhai, FAN Qinyin, et al. Simulation on boiling heat transfer in cooling water jacket of engine[J]. Chinese Internal Combustion Engine Engineering, 2011, 32(4): 76. DOI:10.3969/j.issn.1000-0925.2011.04.015
[8] TALEBI S, ABBASI F, DAVILU H. A 2D numerical simulation of sub-cooled flow boiling at low-pressure and low-flow rates[J]. Nuclear Engineering & Design, 2009, 239(1): 140. DOI:10.1016/j.nucengdes.2008.09.007
[9] 兰治科, 昝元锋, 杨祖毛, 等. 矩形通道单双面加热对过冷沸腾流动换热影响数值分析[J]. 当代化工研究, 2021, 21(9): 48.
LAN Zhike, ZAN Yuanfeng, YANG Zumao, et al. Numerical analysis of one-side and double-side heating influence on subcooled boiling thermal-hydraulic characteristics in rectangular channel[J]. Modern Chemical Research, 2021, 21(9): 48.
[10] 陈二锋, 厉彦忠, 王斯民. 竖直环管内低压水过冷沸腾数值模拟[J]. 西安交通大学学报, 2008, 42(7): 855.
CHEN Erfeng, LI Yanzhong, WANG Simin. Numerical simulation of subcooled boiling water in vertical concentric annulus under low pressure[J]. Journal of Xi'an Jiaotong University, 2008, 42(7): 855. DOI:10.3321/j.issn:0253-987X.2008.07.016
[11] 魏敬华, 潘良明, 袁德文, 等. 过冷流动沸腾相变过程汽泡特性的VOF方法模拟[J]. 核动力工程, 2012, 33(6): 70.
WEI Jinghua, PAN Liangming, YUAN Dewen, et al. VOF simulation of bubble characteristics of subcooled flow boiling[J]. Nuclear Power Engineering, 2012, 33(6): 70. DOI:10.3969/j.issn.0258-0926.2012.06.015
[12] 潘良明, 谭智威. 过冷流动沸腾汽泡凝结变形及流场特性的数值模拟[J]. 重庆大学学报, 2012, 35(6): 57.
PAN Liangming, TAN Zhiwei. Numerical investigation of bubble deformation and flow field characteristics of subcooled boiling during condensation[J]. Journal of Chongqing University, 2012, 35(6): 57. DOI:10.11835/j.issn.1000-582x.2012.06.009
[13] 葛苏槿. 倾斜条件下管内过冷流动沸腾的数值研究[D]. 济南: 山东大学, 2021
GE Sujin. Numerical study on subcooled flow boiling in inclined tube[D]. Jinan: Shandong University, 2021
[14] LEE J, O'NEILL L E, LEE S, et al. Experimental and computational investigation on two-phase flow and heat transfer of highly subcooled flow boiling in vertical upflow[J]. International Journal of Heat and Mass Transfer, 2019, 136: 1214. DOI:10.1016/j.ijheatmasstransfer.2019.03.046
[15] LEE J, O'NEILL L E, MUDAWAR I. 3-D computational investigation and experimental validation of effect of shear-lift on two-phase flow and heat transfer characteristics of highly subcooled flow boiling in vertical upflow[J]. International Journal of Heat and Mass Transfer, 2020, 150: 119291. DOI:10.1016/j.ijheatmasstransfer.2019.119291
[16] LEE J, O'NEILL L E, MUDAWAR I. Computational prediction of key heat transfer mechanisms and hydrodynamic characteristics of critical heat flux (CHF) in subcooled vertical upflow boiling[J]. International Journal of Heat and Mass Transfer, 2020, 161: 120262. DOI:10.1016/j.ijheatmasstransfer.2020.120262
[17] LEE J, MUDAWAR I, HASAN M M, et al. Experimental and computational investigation of flow boiling in microgravity[J]. International Journal of Heat and Mass Transfer, 2022, 183: 122237. DOI:10.1016/j.ijheatmasstransfer.2021.122237
[18] YEO I, LEE S. 2D computational investigation into transport phenomena of subcooled and saturated flow boiling in large length to diameter ratio micro-channel heat sinks[J]. International Journal of Heat and Mass Transfer, 2022, 183: 122128. DOI:10.1016/j.ijheatmasstransfer.2021.122128
[19] CHEN Yujie, LING Kong, DING Hao, et al. 3-D numerical study of subcooled flow boiling in a horizontal rectangular mini-channel by VOSET[J]. International Journal of Heat and Mass Transfer, 2022, 183: 122218. DOI:10.1016/j.ijheatmasstransfer.2021.122218
[20] 曹涛涛. 基于OpenFOAM的过冷流动沸腾热流固耦合模拟研究[D]. 镇江: 江苏大学, 2019
CAO Taotao. Simulation study of thermo-fluid-solid coupling considering subcooled flow boiling based on openfoam[D]. Zhenjiang: Jiangsu University, 2019
[21] ANSYS Inc. ANSYS Fluent theory guide[Z]. Canonsburg: ANSYS Inc, 2020
[22] LEE W H. Pressure iteration scheme for two-phase flow modeling[J]. Multiphase Transport Fundamentals, Reactor Safety Applications, 1980, 1: 407. DOI:10.1142/9789814460286_0004
[23] KIM Y, CHOI J, KIM S, et al. Effects of mass transfer time relaxation parameters on condensation in a thermosyphon[J]. Journal of Mechanical Science and Technology, 2015, 29(12): 5499. DOI:10.1007/s12206-015-1151-5
[24] BERGLES A E, ROHSENOW W M. The determination of forced-convection surface-boiling heat transfer[J]. Journal of Heat Transfer, 1964, 86(3): 369. DOI:10.1115/1.3688697
[25] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335. DOI:10.1016/0021-9991(92)90240-Y
[26] CHEN J C. A correlation for boiling heat transfer to saturated fluids in convective flow[J]. Industrial and Engineering Chemistry Process Design and Development, 1966, 5(3): 323. DOI:10.1021/i260019a023
[27] GUNGOR K E, WINTERTON R H S. A general correlation for flow boiling in tubes and annuli[J]. International Journal of Heat and Mass Transfer, 1986, 29(3): 352. DOI:10.1016/0017-9310(86)90205-X
[28] COOPER M G. Heat flow rates in saturated nucleate pool boiling-a wide-ranging examination using reduced properties[J]. Advances in Heat Transfer, 1984, 16: 204. DOI:10.1016/S0065-2717(08)70205-3
[29] LIU Z, WINTERTON R H S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation[J]. International Journal of Heat and Mass Transfer, 1991, 34(11): 2762. DOI:10.1016/0017-9310(91)90234-6
[30] SHAH M M. A general correlation for heat transfer during subcooled boiling in pipes and annuli[J]. ASHRAE Transactions, 1977, 83(2): 213. DOI:10.1016/S0022-3913(67)80048-9
