周雅夫1,2,孙雪松1,2,连静1,2,孙宵宵1,2
(1.工业装备结构分析国家重点实验室(大连理工大学),大连 116024; 2.大连理工大学 汽车工程学院,大连 116024)
摘要:
为解决燃料电池混合动力公交车中基于优化的能量管理策略难以实车应用的问题,在分析燃料电池公交车(Fuel cell hybrid bus,FCHB)行驶路线的固定性和片段性的基础上,提出了一种基于SOM-K-means(Self-organized mapping K-means)工况识别的能量管理策略。首先,根据公交车站点将行驶路线划分为多个行驶片段,在车辆停站时,运用SOM-K-means二阶聚类模型完成工况识别,获取车辆下一行驶片段的识别协态变量；当车辆在下一个行驶片段运行时,运用识别协态变量完成基于庞特里亚金极值原理(Pontryagins maximum principle,PMP)求解的能量管理策略的实时应用。其次,建立基于公交车实际运行数据的仿真实验,最后建立硬件在环实验,将所提出的策略移植入整车控制器(Vehicle control unit,VCU)中进行实验。实验结果表明,与基于规则的能量管理策略相比,本研究提出的能量管理策略降低了19.77%的平均等效氢气消耗。且该策略在VCU中每一步的计算时间大约为30 ms,计算结果与仿真结果完全一致,满足车辆对能量管理策略的时效性和准确性的要求。
关键词: 燃料电池混合动力公交车 工况识别 庞特里亚金极值原理 能量管理策略 硬件在环
DOI：10.11918/202206048
分类号:TK911
文献标识码:A
基金项目:国家自然科学基金(52172382)
Energy management strategy of fuel cell bus based on working condition identification
ZHOU Yafu1,2,SUN Xuesong1,2,LIAN Jing1,2,SUN Xiaoxiao1,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology), Dalian 116024, China; 2.School of Automotive Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract:
To solve the problem that energy management strategy based on optimization in fuel cell hybrid electric buses is difficult to apply to real life vehicles, an energy management strategy based on SOM-K-means driving condition identification is proposed with reference to the analysis of the fixedness and fragmentation of the fuel cell bus (FCHB) driving route. Firstly, the driving route is divided into driving segments according to bus stops. When the vehicle stops, the SOM-K-means second-order clustering model is used to identify the driving condition, and obtain the predictive co-state of the next driving segment. When the vehicle runs in the next driving segment, a predictive co-state is used to complete the real-time application of the minimum fuel equivalent fuel consumption strategy based on the PMP solution. Secondly, the simulation experiments based on the actual driving data of the bus are established. Finally, the proposed strategy is applied to the vehicle control unit (VCU). The results show that compared with the rule-based strategy, the proposed strategy reduces hydrogen consumption by 19.77%. The calculation time of each step in the VCU is about 30 ms, and the calculation results prove to be completely consistent with the simulation results, meeting the requirements of vehicle for the timeliness and accuracy of energy management strategy.
Key words: fuel cell hybrid bus condition identification Pontryagins maximum principle(PMP) energy management strategies
周雅夫, 孙雪松, 连静, 孙宵宵. 基于工况识别的燃料电池公交车能量管理策略[J]. 哈尔滨工业大学学报, 2023, 55(8): 97-105. DOI: 10.11918/202206048.
ZHOU Yafu, SUN Xuesong, LIAN Jing, SUN Xiaoxiao. Energy management strategy of fuel cell bus based on working condition identification[J]. Journal of Harbin Institute of Technology, 2023, 55(8): 97-105. DOI: 10.11918/202206048.
基金项目 国家自然科学基金(52172382) 作者简介 周雅夫(1962—)，男，教授，博士生导师;
连静(1980—)，女，副教授，博士生导师 通信作者 连静，lianjing@dlut.edu.cn 文章历史 收稿日期: 2022-06-13
Abstract Full text Figures/Tables PDF
基于工况识别的燃料电池公交车能量管理策略
周雅夫1,2, 孙雪松1,2, 连静1,2
, 孙宵宵1,2 1. 工业装备结构分析国家重点实验室(大连理工大学)，大连 116024;
2. 大连理工大学 汽车工程学院，大连 116024
收稿日期: 2022-06-13; 录用日期: 2022-08-12; 网络首发日期: 2023-05-10
基金项目: 国家自然科学基金(52172382)
作者简介: 周雅夫(1962—)，男，教授，博士生导师; 连静(1980—)，女，副教授，博士生导师
通信作者: 连静，lianjing@dlut.edu.cn
摘要: 为解决燃料电池混合动力公交车中基于优化的能量管理策略难以实车应用的问题，在分析燃料电池公交车(Fuel cell hybrid bus, FCHB)行驶路线的固定性和片段性的基础上，提出了一种基于SOM-K-means(Self-organized mapping K-means)工况识别的能量管理策略。首先，根据公交车站点将行驶路线划分为多个行驶片段，在车辆停站时，运用SOM-K-means二阶聚类模型完成工况识别，获取车辆下一行驶片段的识别协态变量；当车辆在下一个行驶片段运行时，运用识别协态变量完成基于庞特里亚金极值原理(Pontryagin's maximum principle, PMP)求解的能量管理策略的实时应用。其次，建立基于公交车实际运行数据的仿真实验，最后建立硬件在环实验，将所提出的策略移植入整车控制器(Vehicle control unit, VCU)中进行实验。实验结果表明，与基于规则的能量管理策略相比，本研究提出的能量管理策略降低了19.77%的平均等效氢气消耗。且该策略在VCU中每一步的计算时间大约为30 ms，计算结果与仿真结果完全一致，满足车辆对能量管理策略的时效性和准确性的要求。
关键词: 燃料电池混合动力公交车 工况识别 庞特里亚金极值原理 能量管理策略 硬件在环
Energy management strategy of fuel cell bus based on working condition identification
ZHOU Yafu1,2, SUN Xuesong1,2, LIAN Jing1,2
, SUN Xiaoxiao1,2 1. State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology), Dalian 116024, China;
2. School of Automotive Engineering, Dalian University of Technology, Dalian 116024, China
Abstract: To solve the problem that energy management strategy based on optimization in fuel cell hybrid electric buses is difficult to apply to real life vehicles, an energy management strategy based on SOM-K-means driving condition identification is proposed with reference to the analysis of the fixedness and fragmentation of the fuel cell bus (FCHB) driving route. Firstly, the driving route is divided into driving segments according to bus stops. When the vehicle stops, the SOM-K-means second-order clustering model is used to identify the driving condition, and obtain the predictive co-state of the next driving segment. When the vehicle runs in the next driving segment, a predictive co-state is used to complete the real-time application of the minimum fuel equivalent fuel consumption strategy based on the PMP solution. Secondly, the simulation experiments based on the actual driving data of the bus are established. Finally, the proposed strategy is applied to the vehicle control unit (VCU). The results show that compared with the rule-based strategy, the proposed strategy reduces hydrogen consumption by 19.77%. The calculation time of each step in the VCU is about 30 ms, and the calculation results prove to be completely consistent with the simulation results, meeting the requirements of vehicle for the timeliness and accuracy of energy management strategy.
Keywords: fuel cell hybrid bus condition identification Pontryagin's maximum principle(PMP) energy management strategies ?
燃料电池具有输出特性软，无法实现制动能量回收等缺点。因此在实际应用中，燃料电池往往需要结合辅助能源组成混合动力系统[1]。而能量管理策略的制定直接影响混合动力系统的经济性。
目前关于能量管理策略的研究主要分为两类：基于规则和基于优化[2]。基于规则的策略倾向于工程应用，由专家根据经验和历史数据制定规则来决定整车的能量分配[3]。而基于优化的策略非常适合解决复杂的非线性系统的能量管理问题，具有更好的优化效果。基于优化的能量管理策略主要分为两种：全局优化和瞬时优化[4]。全局优化需要提前知道车辆的整个行驶工况且计算量大，因此很难应用于实车[5]。而瞬时优化在车辆实际运行过程中根据车辆的状态以及运行情况进行能量的优化分配，因此具有重要的应用意义[6]。
燃料电池混合动力汽车的行驶工况对其经济性有着显著的影响，将工况识别融入到能量管理策略中成为了近些年的研究热点[7-8]。文献[9]通过聚类分析的方法将车辆工况划分为5个典型工况，根据欧几里得接近度进行工况识别。文献[10]从静态和准静态环境的交通信息中识别出车辆模式特征的高影响因子，提出了一种基于数据聚类的车辆路线划分算法，但是初始聚类中心的选择很大程度上会影响聚类分析结果。近年来机器学习在工况识别中得到了进一步应用，BP(back propagation)神经网络和LVQ(learning vector quantization)神经网络选取可以表征车辆工况的特征参数作为输入，对工况样本进行分类[11]。然而神经网络的精度很大程度上受到了自身结构的影响[12]。
本文分析了FCHB行驶路线固定且具有片段性的特点，提出了一种基于SOM-K-means工况识别的实时PMP能量管理策略。首先，根据公交车站点将行驶路线划分为多个行驶片段，在车辆停站时，运用SOM-K-means二阶聚类模型完成工况识别，获取车辆下一行驶片段的识别协态变量；当车辆开始运行时，运用识别协态变量完成基于PMP求解的能量管理策略的实时应用。其次，建立基于公交车实际运行数据的仿真实验，以验证本文所提出策略的燃料经济性。最后将所提出的策略应用到了VCU中，以验证本文所提出策略的实际应用效果。
1 模型的建立 1.1 混合动力系统能量流动模型车辆动力系统模型是设计能量管理策略的基础。本文所研究车辆的动力系统如图 1所示，主要参数见表 1。燃料电池系统(Fuel cell system, FCS)和二次电池是车辆的动力源，DC/DC变换器将燃料电池系统的输出电压升压到电机控制器(Motor control unit, MCU)的母线电压，车辆电气附件包括水泵、气泵、油泵、散热风扇、空调等部件。
Fig. 1
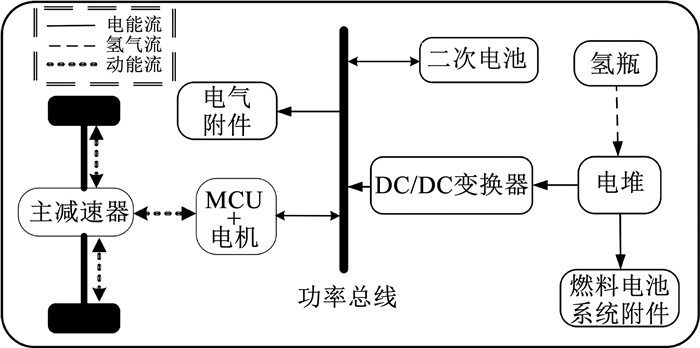图 1 FCHB混合动力系统拓扑结构图 Fig. 1 FCHB hybrid system topology diagram 表 1
表 1 FCHB车辆参数 Tab. 1 FCHB vehicle parameters 整车质量M/kg 二次电池容量Qbat/Ah 电机峰值功率Pmotormax/kW 主减速器传动比ηT 系统峰值功率Pfcsmax/kW 17 000 173 200 6.14 65
燃料电池单体电池数Ncell 二次电池单体电池数Nbat DC/DC转换器效率ηdc 制动能量回收峰值功率/kW
296 189 0.95 -40
表 1 FCHB车辆参数 Tab. 1 FCHB vehicle parameters
混合动力系统的能量流动关系如下：
$P_{\text {bat }}+P_{\text {fcs }}=P_{\text {motor }}+P_{\text {aux }}$ (1)
式中：Pbat为电池输出功率，Pfcs为燃料电池系统的净输出功率，Pmotor为电机输出功率，Paux为整车电气附件消耗功率。
1.2 燃料电池系统模型燃料电池是车辆的主要动力源之一，在设计车辆的能量管理策略时，仅对燃料电池系统的效率、氢气消耗率进行建模即可。
燃料电池的氢气消耗率表达式为[13]
$\dot{m}_{\mathrm{H}_{2}}=\frac{N_{\text {cell }} M_{\mathrm{H}_{2}}}{n_{\mathrm{H}_{2}} F} I_{\text {stack }}$ (2)
式中: MH2为氢气的摩尔质量，nH2为氢气分子的电子数nH2=2, Istack为燃料电池输出电流, F为法拉第常数(96 485 C/mol)。
本文中燃料电池系统效率ηfcs为燃料电池系统的输出功率与其消耗氢气的功率之比：
$\left\{\begin{array}{l}\eta_{\mathrm{fcs}}=\frac{P_{\mathrm{fcs}}}{P_{\mathrm{H}_{2}}}=\frac{P_{\mathrm{fcs}}}{\dot{m}_{\mathrm{H}_{2}} S_{\mathrm{H}_{2}}} \\\dot{m}_{\mathrm{H}_{2}}=\frac{P_{\mathrm{fcs}}}{\eta_{\mathrm{fcs}} S_{\mathrm{H}_{2}}}\end{array}\right.$ (3)
式中: PH2为消耗氢气的功率, SH2为氢气的高热值(143 kJ/g)。
而燃料电池系统效率还可表示为
$\left\{\begin{array}{l}\eta_{\mathrm{fcs}}=\eta_{\text {stack }} \eta_{\mathrm{fc}\_\text { aux }} \\\eta_{\text {stack }}=P_{\text {stack }} / P_{\mathrm{H}_{2}} \\\eta_{\mathrm{fc} \_ \text {aux }}=P_{\mathrm{fcs}} / P_{\text {stack }}=\left(P_{\text {stack }}-P_{\mathrm{fc} \_ \text {aux }}\right) / P_{\text {stack }}\end{array}\right.$ (4)
式中: ηstack为电堆效率，其值为燃料电池电堆输出功率Pstack和消耗的氢气的功率PH2之比；ηfc_aux为燃料电池系统附件效率，其值为燃料电池系统输出功率Pfcs和电堆输出功率Pstack之比；Pfc_aux为燃料电池系统附件(空压机，散热风扇，氢气循环泵)消耗的功率。本文所研究的燃料电池系统效率曲线和燃料电池系统氢气消耗率曲线的多项式拟合结果如图 2所示。
Fig. 2
图 2 FCS系统效率和耗氢率曲线 Fig. 2 FCS efficiency and hydrogen consumption rate curve 1.3 二次电池模型本文选择锂电池作为所研究车辆的辅助动力源，对锂电池建立Rint模型，如图 3(a)所示。在本文所研究的车辆中，单体锂电池的Uoc, Rbat和电池荷电状态(State of charge，SOC)的关系如图 3(b)所示。其中，Uoc为开路电压，Ibat为电池输出电流，Rbat为内阻，UDC为输出电压，二次电池的Uoc和Rbat主要由电池的荷电状态大小FSOC决定。各参数之间的关系如下[14]:
$\left\{\begin{array}{l}F_{\mathrm{SOC}}(t+\Delta t)=F_{\mathrm{SOC}}(t)+\frac{I_{\text {bat }}(t) \Delta t}{Q_{\text {bat }}} \\I_{\text {bat }}(t)=\frac{U_{\mathrm{oc}}(t)-\sqrt{U_{\mathrm{oc}}^{2}(t)-4 R_{\text {bat }}(t) P_{\text {bat }}(t)}}{2 R_{\text {bat }}(t)} \\U_{\mathrm{dc}}=U_{\text {oc }}(t)-I_{\text {bat }}(t) R_{\text {bat }}(t)\end{array}\right.$ (5)
Fig. 3
图 3 二次电池的Rint模型 Fig. 3 Rint model of secondary battery 电池的实时充电效率和实时放电效率计算公式如下[15]：
$\left\{\begin{array}{l}\eta_{\mathrm{dis}}=\frac{1+\sqrt{1-\frac{4 R_{\mathrm{bat}} P_{\mathrm{bat}}}{U_{\mathrm{oc}}^{2}}}}{2}, P_{\text {bat }} \geqslant 0 \\\eta_{\mathrm{chr}}=\frac{2}{1+\sqrt{1-\frac{4 R_{\mathrm{bat}} P_{\mathrm{bat}}}{U_{\mathrm{oc}}^{2}}}}, P_{\mathrm{bat}}<0\end{array}\right.$ (6)
1.4 边界模型确保FCS和二次电池安全稳定运行是制定能量管理策略的基本要求。因此，整个混合动力系统需要满足以下边界条件：
$\left\{\begin{array}{l}P_{\mathrm{fcs}}^{\min } \leqslant P_{\mathrm{fcs}} \leqslant P_{\mathrm{fcs}}^{\max } \\P_{\mathrm{bat}}^{\min } \leqslant P_{\mathrm{bat}} \leqslant P_{\mathrm{bat}}^{\max } \\F_{\mathrm{soc}}^{\mathrm{min}} \leqslant P_{\mathrm{soc}} \leqslant P_{\mathrm{soc}} \\\dot{P}_{\mathrm{fcs}}^{\min } \leqslant P_{\mathrm{fcs}} \leqslant \dot{P}_{\mathrm{fcs}}^{\max }\end{array}\right.$ (7)
式中, 上标min、max分别为各个变量取值的下限、上限。
2 基于工况识别的实时能量管理策略 2.1 能量管理策略总体架构本文提出的能量管理策略的结构如图 4所示，主要由离线优化和在线控制两部分构成。
Fig. 4
图 4 能量管理模型结构 Fig. 4 Energy management model structure 1) 离线优化。在公交车历史行驶循环中采集电机输出功率组成历史数据集，提取每个历史行驶片段对应的工况特征值，形成历史工况特征值表。随后对相同地理位置的行驶片段进行聚类分析，得到历史行驶片段的聚类结果。同时利用粒子群优化算法(Particle swarm optimization, PSO)获取各个历史行驶片段对应的PMP算法中的最优协态变量。
2) 在线控制。包括车辆工况识别阶段和策略运行阶段。①车辆工况识别阶段。当车辆停在公交站台时，提取车辆的上一行驶片段的特征值，对上一行驶片段进行工况识别。本文选择每个行驶片段的电机输出功率在不同区间的比例作为工况识别的特征参数[10]，具体的识别方法为：计算上一行驶片段的特征值与处于同一位置历史行驶片段的特征值的聚类中心的欧氏距离，从而判断上一个行驶片段的所属簇。然后预测车辆的下一个行驶片段的识别协态变量，具体的预测方式为：将与上一个行驶片段属于同一簇的历史行驶片段所对应的下一行驶片段的最优协态变量平均化，从而得到当前行驶循环的下一行驶片段的识别协态变量。当车辆位于始发站时，由于无法提取上一行驶片段的特征值进行工况识别，因此将该地理位置上的所有历史行驶片段的最优协态变量平均化，作为车辆在当前行驶循环的第1个行驶片段的识别协态变量。②策略运行阶段。当车辆越过公交站台开始行驶片段的运行时，利用在工况识别阶段时得到的识别协态变量，运用基于PMP求解的能量管理策略，实时地进行能量分配。
2.2 车辆行驶循环和行驶片段的定义由于公交车的行驶路线相对固定，且具有很强的片段性，因此可对车辆的行驶路线进行行驶片段划分，将每两个公交站点之间的区域作为一个行驶片段(Driving segment, DS)，将车辆从始发站到终点站再返回始发站的行程作为一个行驶循环(Driving cycle, DC)。本文所研究的车辆运行于辽宁省大连市535路公交路线，该路线东起于马栏广场公交站，西起于鞍子岭公交站，单趟行程31个站，双趟行程共60个站。因此本文中一个DC包括60个DS。
2.3 基于K-means的一阶聚类分析K-means现已成为信息处理领域和数据关联性挖掘领域中最常见的分析方法之一，其基本思想为通过不断地迭代求解计算出各类的聚类中心[16]。
标准的K-means聚类算法是将k个初始聚类中心进行分配和更新的交替迭代，直至收敛[17]。本文中设置的K-means聚类中心的收敛误差为10-6。
在使用K-means聚类时，聚类数目的选取非常重要。聚类数目过少，则无法充分挖掘数据的全部信息；聚类数目过大，不仅会使计算量大幅增加，而且会割裂相似数据之间的联系[18]。因此本文采用肘部法确定各个地理位置的历史行驶片段的最优聚类数目，各个地理位置的行驶片段的最优聚类数目如图 5所示。
Fig. 5
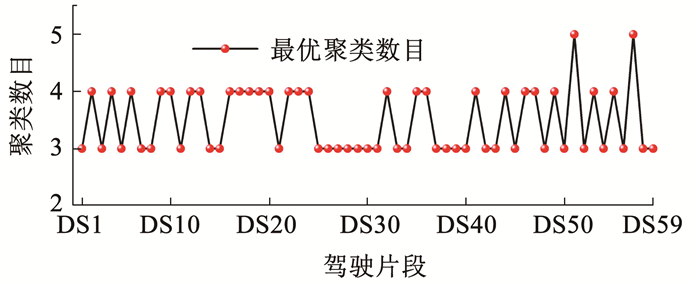图 5 行驶片段最优聚类数目 Fig. 5 Optimal number of clusters for DS 2.4 基于K-means和SOM的二阶聚类分析基于聚类方法对车辆的每一个行驶片段进行工况识别的准确性很大程度上依赖聚类结果的准确性和合理性。K-means聚类方法中聚类结果受初始聚类中心的影响非常大，若初始聚类中心选择不合理，则容易使聚类过程陷入局部最优。SOM神经网络聚类方法通过自组织学习，可产生稳定的聚类中心，但其聚类结果的物理几何意义不明显。因此本文综合了K-means和SOM的优势，采用SOM对历史工况进行一阶聚类，将其产生的聚类中心作为K-means的初始聚类中心进行二阶聚类，避免了因初始聚类中心选择不合理带来的聚类效果不佳。SOM神经网络的结构图如图 6所示。
Fig. 6
图 6 SOM神经网络结构图 Fig. 6 SOM neural network structure diagram 基于SOM-K-means的历史工况二阶聚类算法流程如图 7所示。在训练SOM神经网络时，输出神经元数目代表聚类数目。因此本文在对每一地理位置的行驶片段进行聚类时，利用肘部法求得的最佳聚类数作为输出层神经元数。
Fig. 7
图 7 SOM-K-means二阶聚类流程图 Fig. 7 SOM-K-means two-order clustering flowchart SOM神经网络流程如下：
1) 对输出层网络权向量wij进行初始化处理，j=1, 2, …, m; i=1, 2, …, n, 初始化获胜域半径Nj*(0) 和学习率β(0)，m为输出层神经元数目。n为输入层神经元数目。
2) 把输入向量xi=(x1, x2, …, xp) 输入给输出层。p为输入向量的维数，即特征值的维数，本文中p=10。
3) 计算输出层节点和输入向量之间的欧氏距离，通过计算得到一个具有最小距离的神经元，将其作为获胜神经元j*。
4) 更新获胜神经元j*的获胜邻域Nj*(t)以及学习率β(t, N)，t为迭代次数。更新学习率的公式为
$\left\{\begin{array}{l}\beta(t, N)=\beta(t) \mathrm{e}^{-N} \\\beta(t)=\beta(0) \mathrm{e}^{\left(-\frac{t}{t_{\max }}\right)}\end{array}\right.$ (8)
式中N为常数，取为2。
5) 通过更新公式修正优胜邻域内神经元的权值向量。更新公式如下：
$\boldsymbol{w}_{i j}(t+1)=\boldsymbol{w}_{i j}(t)+\beta(t, N)\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{i j}(t)\right)$ (9)
6) 判断训练过程是否满足结束训练的条件。在本文中训练结束的条件为：①训练迭代次数大于迭代阈值。②学习率β(t, N)＜βmin。当满足结束条件中的任意一个训练结束。否则返回步骤2)继续训练。
2.5 基于PMP求解的等效消耗最小策略车辆的混合动力系统是一个复杂的非线性系统，燃料电池、二次电池必须满足式(7)所示的边界模型。为解决该系统的能量分配问题，引入庞特里亚金极值原理，选择Pfcs为控制变量，选择二次电池Fsoc为状态变量，构建哈密顿函数H如下[19]：
$H=\dot{m}_{\mathrm{fc}}\left(P_{\mathrm{fcs}}(t)\right)+\alpha(t) \dot{F}_{\mathrm{soc}}(t)$ (10)
式中：
在满足约束模型的基础上，要最小化H，需要在每一个时间点找到最优的控制变量Pfcs(t)使得哈密顿函数H最小，因此优化问题变成了Pfcs(t)在约束条件下的极小值求解，即
$P_{\mathrm{fcs}}^{*}(t)=\arg \ \min (H)$ (11)
最优控制变量Pfcs*(t)和最优状态变量Fsoc*(t)满足下式[20]：
$\left\{\begin{array}{l}\frac{\partial H}{\partial \alpha}=\dot{F}_{\mathrm{soc}}^{*} \\\frac{\partial H}{\partial \dot{F}_{\mathrm{soc}}^{*}}=\dot{\alpha} \\\frac{\partial H}{\partial P_{\mathrm{fcs}}^{*}}=0\end{array}\right.$ (12)
2.6 基于PSO求解历史行驶片段的最优协态变量设计历史工况下的最优能量管理策略，实质上就是求解历史工况下各个行驶片段的最优协态变量。本文利用粒子群算法(PSO)对最优协态变量进行求解，建立的优化目标函数如下：
$ J=\int_{t_{\text {begin }}}^{t_{\text {end }}}\left(\dot{m}_{\mathrm{fc}}(t)+m_{\mathrm{B}}(t)\right) \mathrm{d} t $ (13)
$ \dot{m}_{\mathrm{B}}(t)=\frac{\eta(t) P_{\text {bat }}(t)}{S_{\mathrm{H}_{2}}}$ (14)
$\eta(t)= \begin{cases}\frac{1}{\bar{\eta}_{\mathrm{fc} \_ \text {sys }} \bar{\eta}_{\mathrm{chg}} \eta_{\mathrm{dis}}(t)}, & P_{\text {bat }} \geqslant 0 \\\frac{\eta_{\mathrm{chg}}(t)}{\bar{\eta}_{\mathrm{fc} \_ \text {sys }} \bar{\eta}_{\mathrm{dis}}}, & P_{\text {bat }}<0\end{cases}$ (15)
式中：
粒子群算法(PSO)根据鸟群觅食行为而产生的一种优化算法[21]。PSO算法的输入为协态变量α，适应度函数为J。优化过程的流程图如图 8所示。
Fig. 8
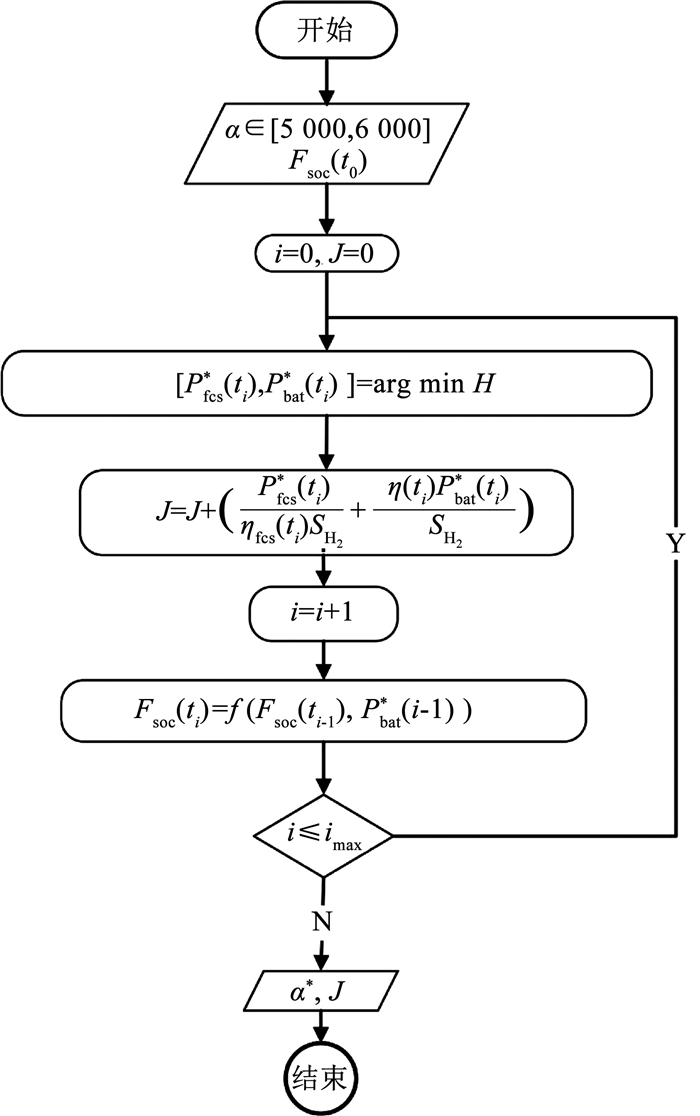图 8 PSO优化算法流程图 Fig. 8 PSO optimization algorithm flow chart 3 实验与分析 3.1 车辆的工况识别效果验证协态变量在能量分配中发挥着关键的作用，在历史工况下已经求解得到车辆的每一个行驶片段的最优协态变量，而在未知工况的行驶片段中，车辆将运用本文提出的方法得到的识别协态变量进行能量分配。
本文总共采集了32个DC的车辆运行数据，为了验证车辆工况识别的准确性，选取5个DC作为在线工况，命名为DC1、DC2、DC3、DC4和DC5，将剩下的27个DC作为历史工况用于训练。
将在线DC中的最优协态变量作为标准值，比较利用本文提出的策略得到的识别协态变量与最优协态变量之间的差异，以验证本文提出的基于工况识别的方法得到识别协态变量的合理性。
图 9展示了分别使用一阶聚类模型和二阶聚类模型对历史工况进行聚类时，在线行驶循环的最优协态变量和识别协态变量之间的平均绝对误差(MAE)。结果表明，二阶聚类模型得到了更准确的协态变量，具有更好的工况识别效果。
Fig. 9
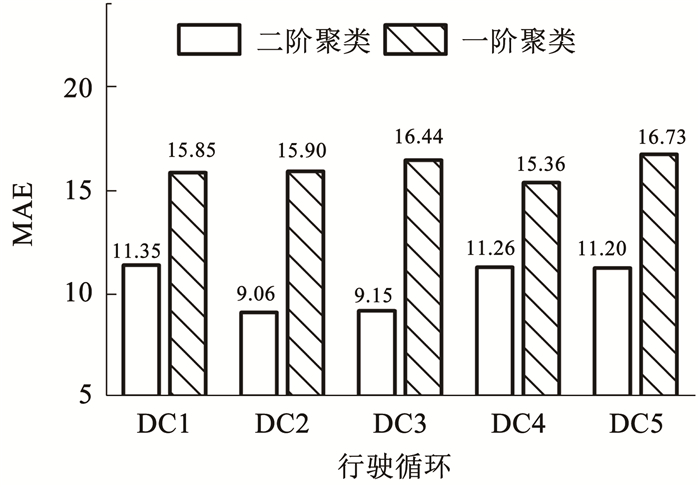图 9 测试行驶循环协态变量MAE Fig. 9 Test driving segment covariate MAE 3.2 对比实验的设计为验证本文提出的能量管理模型的有效性，设计了如下5组对比试验。在这5组对比实验中，测试工况同样为行驶循环DC1、DC2、DC3、DC4和DC5，训练工况同样为剩余的27个行驶循环。
1) 工况已知。在路况已知的情况下运用最优协态变量进行仿真。
2) 二阶模型。在基于路况未知的情况下，使用对历史工况二阶聚类后的结果，对车辆进行工况识别，运用识别协态变量进行仿真。
3) 一阶模型。在基于路况未知的情况下，使用对历史工况一阶聚类后的结果，对车辆进行工况识别，运用次优识别协态变量进行仿真。
4) 基于规则。本文中所用到的数据来自实车运行过程中，因此增加一组实车对比试验。实车上运行的策略为基于规则的能量管理策略。
5) 硬件在环。硬件在环实验，将基于二阶聚类识别的策略移植到了大连市氢能示范项目中的燃料电池混合动力公交车的整车控制器(VCU)中，上位机利用CAN总线通讯方式将电机功率发送给VCU，随后VCU将计算结果发送到上位机。
在仿真实验中，为了便于分析，将实验中二次电池的初始SOC均设置为0.7。5组实验对比的主要指标为总等效耗氢量。
3.3 实验结果分析下面对不同组对比实验中行驶循环DC1、DC2、DC3、DC4和DC5对应的车辆运行结果进行总结和分析。
图 10展示了在上述5组不同的实验中5个在线行驶循环的等效氢气消耗量。表 2中展示了相比于基于规则的策略，各组实验中节省的氢气消耗量百分比。从图 10和表 2中可以看到，与基于规则的策略相比，在工况已知下运用最优协态变量执行能量管理策略有着最优的节省等效氢气效果，在5个在线行驶循环中分别节省氢气17.27%~25.24%，平均节省氢气20.01%。与基于规则的策略相比，基于二阶聚类的策略使用识别协态变量来执行能量管理策略有着次优的氢气节省效果，在5个在线行驶循环中分别节省氢气17.02%~25.16%，平均节省氢气19.77%，与工况已知下的平均氢气节省百分比相差0.24%。而在基于一阶聚类的策略中，5个在线行驶循环分别节省氢气16.20%~23.89%，平均节省氢气18.80%，与工况已知下的氢气节省百分比相差1.21%，与二阶聚类下的氢气节省百分比相差0.97%。结果表明，一方面本文所提出的基于SOM-K-means二阶聚类模型进行工况识别的能量管理策略具有很好的燃料经济性，可以很大程度上减少氢气消耗。另一方面，与基于工况已知的能量管理策略相比，基于二阶聚类模型工况识别的策略仅仅多了0.24%的氢气消耗，与基于一阶聚类模型工况识别的能量管理策略相比，基于二阶聚类模型工况识别的策略节省了0.97%的氢气，说明了本文所提出的工况识别方法起到了很好的效果。
Fig. 10
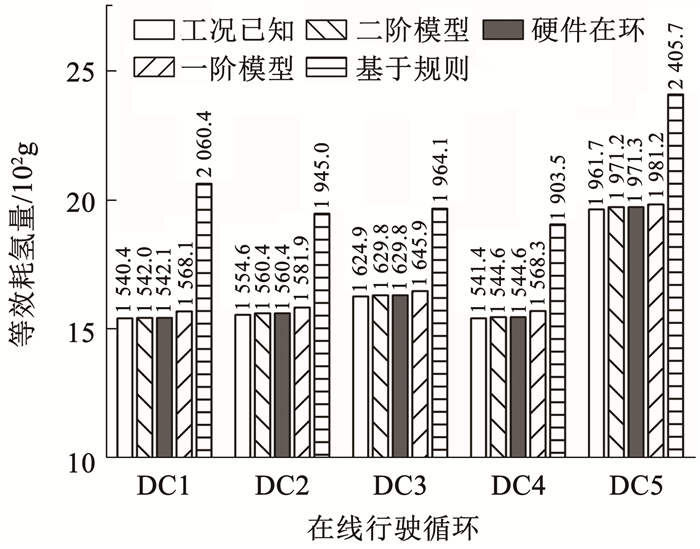图 10 耗氢量对比图 Fig. 10 Comparison chart of hydrogen consumption 表 2
表 2 5组仿真实验氢气消耗节省百分比 Tab. 2 Hydrogen consumption savings percentage of 5 experiments? %行驶循环 氢气消耗节省百分比
工况已知 二阶模型 硬件在环 一阶模型
DC1 25.24 25.16 25.16 23.89
DC2 20.07 19.77 19.77 18.67
DC3 17.27 17.02 17.02 16.20
DC4 19.02 18.85 18.85 17.61
DC5 18.46 18.06 18.06 17.65
表 2 5组仿真实验氢气消耗节省百分比 Tab. 2 Hydrogen consumption savings percentage of 5 experiments?
在不同的能量管理策略中，整车燃料消耗的差异主要和动力电池的热量损耗和燃料电池系统的附件损耗有关系。为了提升整车的燃料经济性，应该尽可能地减少动力电池的热量损耗，提高燃料电池系统在高效率区间的使用率。图 2中描述了燃料电池系统的高效率区间为[10 kW, 30 kW]，表 3展示了不同实验下的5个行驶循环燃料电池系统高效区间的使用率。从表 3中可以看出，在工况已知的能量管理策略中，燃料电池系统高效区间使用率分别为61.85%~66.98%，其平均使用率为65.34%；在基于二阶聚类的能量管理策略中，燃料电池系统高效区间使用率分别为61.43%~66.41%，其平均使用率为64.52%；在基于一阶聚类的能量管理策略中，燃料电池系统高效区间使用率分别为59.97%~66.37%，其平均使用率为63.81%，而基于规则的策略，燃料电池系统高效区间使用率分别为2.65%~4.58%，其平均使用率为3.31%。因此相比较于基于规则的策略，本文提出的能量管理策略可使燃料电池较长时间工作在高效区间，更有助于减少整车的等效氢气消耗。
表 3
表 3 5组仿真实验燃料电池高效区间使用率 Tab. 3 Hydrogen consumption savings percentage of 5 experiments? %行驶循环 燃料电池高效区间使用率
工况已知 二阶模型 一阶模型 基于规则
DC1 66.98 66.41 66.37 2.65
DC2 61.85 61.43 59.97 3.05
DC3 66.64 65.74 65.28 2.96
DC4 66.08 64.29 64.02 4.58
DC5 65.13 64.74 63.39 3.31
表 3 5组仿真实验燃料电池高效区间使用率 Tab. 3 Hydrogen consumption savings percentage of 5 experiments?
表 4展示了不同仿真试验下的5个行驶循环的终止SOC。可以看出5个行驶循环的终止SOC均处于二次电池的高效工作区间[0.3-0.9]，因此本文所提出的能量管理策略可以有效的避免二次电池过充或者过放。
表 4
表 4 4组仿真实验终止SOC结果 Tab. 4 Final SOC results of 4 experiments 行驶循环 实验终止SOC 工况已知 二阶模型 一阶模型 硬件在环
DC1 0.621 3 0.598 8 0.590 2 0.598 8
DC2 0.602 3 0.591 6 0.592 2 0.591 7
DC3 0.597 3 0.589 0 0.579 2 0.588 9
DC4 0.593 5 0.571 9 0.570 1 0.571 9
DC5 0.538 0 0.532 5 0.521 6 0.532 5
表 4 4组仿真实验终止SOC结果 Tab. 4 Final SOC results of 4 experiments
为了验证所提出策略的实际可应用性，本文建立了硬件在环实验，并与仿真实验进行对比。从图 10中可以看出，在硬件在环与仿真中，两者的等效氢气消耗量是完全吻合的。从表 4中可以看出，硬件在环与仿真实验中5个行驶循环的终止SOC完全一致。为了更详细地对比两组实验中的能量分配过程，图 11中展示了两种实验中5个在线行驶循环对应的二次电池的SOC变化曲线，图 12中展示了其二次电池的输出功率曲线。从图 11、12中可以看出，仿真结果和硬件在环实验结果完全吻合，这说明了本文提出的基于二阶聚类的实时能量管理策略完全可以在VCU中运行，且具有和仿真实验同样的结果，并再次验证了本文仿真结果的准确性。
Fig. 11
图 11 SOC曲线 Fig. 11 The SOC curve Fig. 12
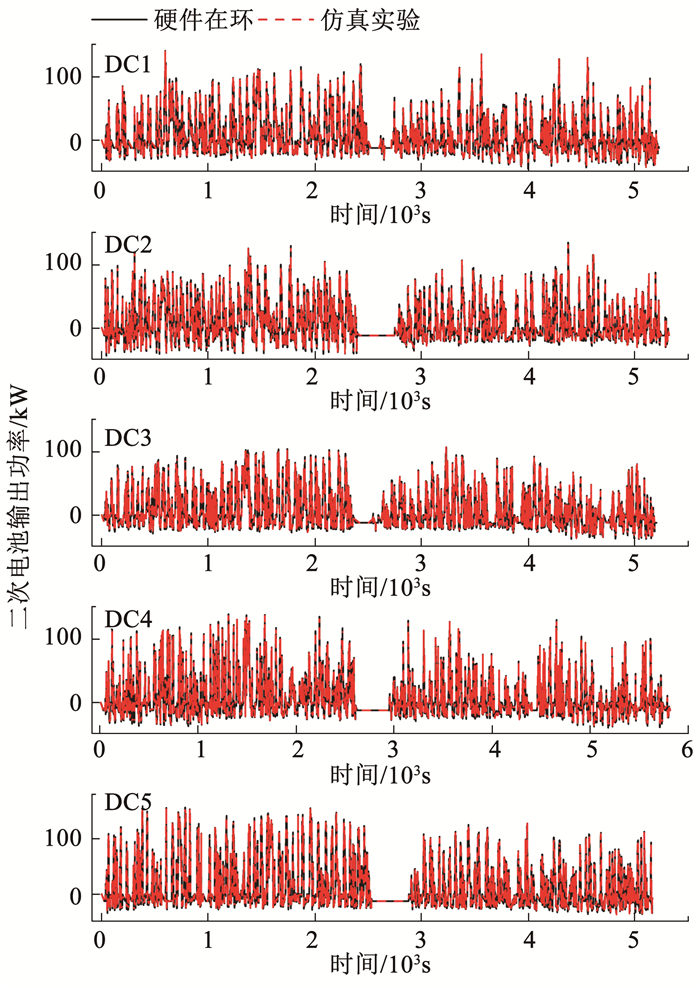图 12 二次电池输出功率曲线 Fig. 12 Secondary battery output power curve 图 13展示了硬件在环实验的部分原始数据，从图中可以清晰的看出，从给VCU发送CAN报文到VCU将计算结果发送出来，时间大约消耗30 ms，能量分配的计算步长(1 s)，因此满足车辆对能量管理策略时效性的要求。
Fig. 13
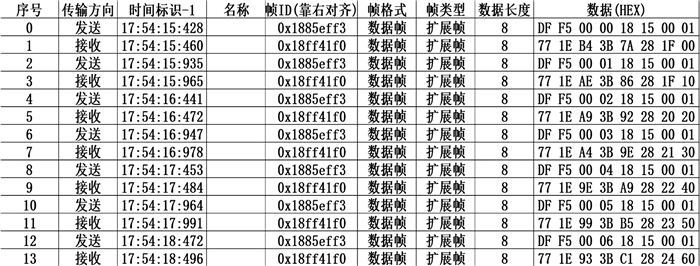图 13 硬件在环实验结果 Fig. 13 Hardware-in-the-loop experimental results 综上所述可得, 首先本文所提出的基于二阶聚类识别的实时能量管理策略具有非常低的氢气消耗量，可以极大的减少公交车在行驶时的能量消耗。其次，本文所提出来的基于二阶聚类识别的实时能量管理策略可以在VCU中运行，并且满足车辆对能量管理策略的时效性和准确性的要求。
4 结论1) 与基于规则的实车数据相比，在本文所提出的基于二阶聚类识别的策略中，等效耗氢量平均下降19.77%；与基于工况已知下的仿真结果(20.01%)相比，平均能耗差异相差0.24%。这一结果表明本文提出的方法可以大幅减少公交车的耗氢量，对于FCHB的发展起到了积极的作用。
2) 将本文所提出的能量管理策略移植到了大连氢能示范项目中燃料电池混合动力汽车的VCU中，根据实验结果显示，VCU的计算时间大约为30 ms，且计算结果与仿真结果完全吻合。说明本文提出的方法可以在VCU运行，为将来基于优化的能量管理策略应用于FCHB中打下了坚实的基础。
参考文献
[1] 曾小华, 牛超凡, 宋大凤, 等. 燃料电池汽车深度节能分析[J]. 哈尔滨工业大学学报, 2021, 53(7): 77.
ZENG Xiaohua, NIU Chaofan, SONG Dafeng, et al. Deep energy-saving analysis of fuel cell vehicles[J]. Journal of Harbin Institute of Technology, 2021, 53(7): 77. DOI:10.11918/202006106
[2] ZHOU Yang, LI Huan, RAVEY A, et al. An integrated predictive energy management for light-duty range-extended plug-in fuel cell electric vehicle[J]. Journal of Power Sources, 2020, 451: 227780. DOI:10.1016/j.jpowsour.2020.227780
[3] LIN Xinyou, WANG Zhaorui, ZENG Songrong, et al. Real-time optimization strategy by using sequence quadratic programming with multivariate nonlinear regression for a fuel cell electric vehicle[J]. International Journal of Hydrogen Energy, 2021, 46(24): 13240. DOI:10.1016/j.ijhydene.2021.01.125
[4] WANG Yongqiang, MOURA S J, ADVANI S G, et al. Power management system for a fuel cell/battery hybrid vehicle incorporating fuel cell and battery degradation[J]. International Journal of Hydrogen Energy, 2019, 44(16): 8479. DOI:10.1016/j.ijhydene.2019.02.003
[5] SUN Haochen, FU Zhumu, TAO Fazhan, et al. Data-driven reinforcement-learning-based hierarchical energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles[J]. Journal of Power Sources, 2020, 455: 227964. DOI:10.1016/j.jpowsour.2020.227964
[6] MARZOUGUI H, KADRI A, MARTIN J P, et al. Implementation of energy management strategy of hybrid power source for electrical vehicle[J]. Energy Conversion and Management, 2019, 195: 830. DOI:10.1016/j.enconman.2019.05.037
[7] SHI Junzhe, XU Bin, SHEN Yimin, et al. Energy management strategy for battery/supercapacitor hybrid electric city bus based on driving pattern recognition[J]. Energy, 2022, 243: 122752. DOI:10.1016/j.energy.2021.122752
[8] SONG Ke, LI Feiqiang, HU Xiao, et al. Multi-mode energy management strategy for fuel cell electric vehicles based on driving pattern identification using learning vector quantization neural network algorithm[J]. Journal of Power Sources, 2018, 389: 230. DOI:10.1016/j.jpowsour.2018.04.024
[9] LEI Zhenzhen, CHENG Dong, LIU Yonggang, et al. A dynamic control strategy for hybrid electric vehicles based on parameter optimization for multiple driving cycles and driving pattern recognition[J]. Energies, 2017, 10(1): 54. DOI:10.3390/en10010054
[10] SUN Xiaoxiao, ZHOU Yafu, HUANG Lijian, et al. A real-time PMP energy management strategy for fuel cell hybrid buses based on driving segment feature recognition[J]. International Journal of Hydrogen Energy, 2021, 46(80): 39983. DOI:10.1016/j.ijhydene.2021.09.204
[11] ZHENG Yongliang, HE Feng, SHEN Xinze, et al. Energy control strategy of fuel cell hybrid electric vehicle based on working conditions identification by least square support vector machine[J]. Energies, 2020, 13(2): 426. DOI:10.3390/en13020426
[12] HAN Xuefeng, HE Hongwen, WU Jingda, et al. Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle[J]. Applied Energy, 2019, 254: 113708. DOI:10.1016/j.apenergy.2019.113708
[13] MENG Xiang, LI Qi, ZHANG Guorui, et al. A dual-mode energy management strategy considering fuel cell degradation for energy consumption and fuel cell efficiency comprehensive optimization of hybrid vehicle[J]. IEEE Access, 2019, 7: 134475. DOI:10.1109/ACCESS.2019.2939047
[14] 吕沁阳, 滕腾, 张宝迪, 等. 增程式燃料电池车经济性与耐久性优化控制策略[J]. 哈尔滨工业大学学报, 2021, 53(7): 126.
LV Qinyang, TENG Teng, ZHANG Baodi, et al. Optimal control strategy for economy and durability of extended range fuel cell vehicle[J]. Journal of Harbin Institute of Technology, 2021, 53(7): 126. DOI:10.11918/202008115
[15] ZHENG Chunhua, LI Wei, LI Weimin, et al. A deep reinforcement learning-based energy management strategy for fuel cell hybrid buses[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2022, 9(3): 885. DOI:10.1007/s40684-021-00403-x
[16] 李宾. 基于出行工况预测的燃料电池汽车能量管理策略研究[D]. 长春: 吉林大学, 2021
LI Bin. Research on energy management strategy of fuel cell vehicle based on driving condition prediction[D]. Changchun: Jilin University, 2021. DOI: 10.27162/d.cnki.gjlin.2021.004942
[17] 刘凤. K-means算法类簇中心优化研究[D]. 贵阳: 贵州大学, 2021
LIU Feng. Research on cluster center optimization of K-means algorithm[D]. Guiyang: Guizhou University, 2021. DOI: 10.27047/d.cnki.ggudu.2021.000344
[18] SONG Ke, WANG Xiaodi, LI Feiqiang, et al. Pontryagin's minimum principle-based real-time energy management strategy for fuel cell hybrid electric vehicle considering both fuel economy and power source durability[J]. Energy, 2020, 205: 118064. DOI:10.1016/j.energy.2020.118064
[19] LI Xiyun, WANG Yujie, YANG Duo, et al. Adaptive energy management strategy for fuel cell/battery hybrid vehicles using Pontryagin's Minimal Principle[J]. Journal of Power Sources, 2019, 440: 227105. DOI:10.1016/j.jpowsour.2019.227105
[20] DU Aimin, CHEN Yaoyi, ZHANG Dongxu, et al. Multi-objective energy management strategy based on PSO optimization for power-split hybrid electric vehicles[J]. Energies, 2021, 14(9): 2438. DOI:10.3390/en14092438
[21] 于烨, 黄默, 段涛, 等. 粒子群优化加权灰色回归组合的卫星钟差预报[J]. 哈尔滨工业大学学报, 2020, 52(10): 144.
YU Ye, HUANG Mo, DUAN Tao, et al. Satellite clock bias prediction based on particle swarm optimization and weighted grey regression combined model[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 144. DOI:10.11918/201911175
