夏成亮1,2,史庆轩1,2,王震1,2
(1.结构工程与抗震教育部重点实验室(西安建筑科技大学),西安 710055;2.西安建筑科技大学 土木工程学院,西安 710055)
摘要:
为更精确地预测无抗冲切钢筋的钢筋混凝土（RC）板柱节点受冲切承载力,结合梁剪压破坏机理和修正压力场理论（MCFT）,提出一种新的板柱受冲切承载力计算方法。首先,假定无抗冲切钢筋的RC板柱节点冲切荷载由上部剪压区混凝土提供的受剪承载力、斜拉区及受拉区中的骨料咬合力和钢筋的销栓作用共同承担；其次,分析剪压区和斜拉区及受拉区的不同受力状态,分别建立剪压区抗剪承载力计算式和斜拉区及受拉区抗剪承载力计算式；然后,通过统计分析和理论推导得到临界斜裂缝倾角、剪压区高度和受压区高度的计算公式；最后将两部分的抗冲切承载力贡献叠加,建立无抗冲切钢筋的RC板柱节点的受冲切承载力计算方法。使用该计算方法对文献中54个板柱节点试验结果进行验算,计算结果与试验值吻合较好,且变异系数较小。该计算方法可用于无抗冲切钢筋的RC板柱节点的冲切承载力的计算。
关键词: 修正压力场理论 板柱节点 剪压区高度 临界斜裂缝倾角 冲切承载力
DOI：10.11918/202106064
分类号:TU375.2
文献标识码:A
基金项目:国家自然科学基金(51878540)
Calculation of punching shear capacity of RC slab-column connections without shear reinforcement
XIA Chengliang1,2,SHI Qingxuan1,2,WANG Zhen1,2
(1.Key Lab of Structural Engineering and Earthquake Resistance (Xi’an University of Architecture and Technology), Ministry of Education, Xi’an 710055, China; 2.School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)
Abstract:
In order to predict the punching shear capacity of slab-column connections more accurately, a new calculation method for punching shear capacity of slab-column connections was proposed based on the beam shear failure mechanism and modified compression-field theory (MCFT). Firstly, it was assumed that the punching load of reinforced concrete (RC) slab-column connections without shear reinforcement was jointly provided by the concrete in the upper shear compression zone, the aggregate interlock force in the cable-stayed zone, and the dowel action in the tension zone. Secondly, the different stress states of shear compression zone, cable-stayed zone, and tension zone were analyzed, and the shear bearing capacity calculation formulas of shear compression zone, cable-stayed zone, and tension zone were established respectively. Then, through statistical analysis and theoretical derivation, the calculation formulas of the heights of shear compression zone and compression zone, as well as the critical inclined crack angle were obtained. Finally, the contributions of the two parts of the punching resistance capacity were superimposed to establish the calculation method of punching shear capacity of RC slab-column connections without shear reinforcement. The calculation method was applied to predict the ultimate punching shear strength of 54 slab-column connections in relevant literature. Results show that the calculated values were in good agreement with the experimental values, and the variation coefficient was small. The proposed calculation method can be used to calculate the ultimate punching shear strength of RC slab-column connections without shear reinforcement.
Key words: modified compression-field theory slab-column connection shear compression zone height critical inclined crack angle punching shear strength
夏成亮, 史庆轩, 王震. 无抗冲切钢筋的RC板柱节点受冲切承载力计算[J]. 哈尔滨工业大学学报, 2022, 54(4): 18-24. DOI: 10.11918/202106064.
XIA Chengliang, SHI Qingxuan, WANG Zhen. Calculation of punching shear capacity of RC slab-column connections without shear reinforcement[J]. Journal of Harbin Institute of Technology, 2022, 54(4): 18-24. DOI: 10.11918/202106064.
基金项目 国家自然科学基金(51878540) 作者简介 夏成亮(1994—)，男，博士研究生;
史庆轩(1963—)，男，教授，博士生导师 通信作者 史庆轩，shiqx@xauat.edu.cn 文章历史 收稿日期: 2021-06-15
Abstract Full text Figures/Tables PDF
无抗冲切钢筋的RC板柱节点受冲切承载力计算
夏成亮1,2, 史庆轩1,2
, 王震1,2 1. 结构工程与抗震教育部重点实验室(西安建筑科技大学)，西安 710055;
2. 西安建筑科技大学 土木工程学院，西安 710055
收稿日期: 2021-06-15
基金项目: 国家自然科学基金(51878540)
作者简介: 夏成亮(1994—)，男，博士研究生; 史庆轩(1963—)，男，教授，博士生导师
通信作者: 史庆轩，shiqx@xauat.edu.cn
摘要: 为更精确地预测无抗冲切钢筋的钢筋混凝土(RC)板柱节点受冲切承载力，结合梁剪压破坏机理和修正压力场理论(MCFT)，提出一种新的板柱受冲切承载力计算方法。首先，假定无抗冲切钢筋的RC板柱节点冲切荷载由上部剪压区混凝土提供的受剪承载力、斜拉区及受拉区中的骨料咬合力和钢筋的销栓作用共同承担；其次，分析剪压区和斜拉区及受拉区的不同受力状态，分别建立剪压区抗剪承载力计算式和斜拉区及受拉区抗剪承载力计算式；然后，通过统计分析和理论推导得到临界斜裂缝倾角、剪压区高度和受压区高度的计算公式；最后将两部分的抗冲切承载力贡献叠加，建立无抗冲切钢筋的RC板柱节点的受冲切承载力计算方法。使用该计算方法对文献中54个板柱节点试验结果进行验算，计算结果与试验值吻合较好，且变异系数较小。该计算方法可用于无抗冲切钢筋的RC板柱节点的冲切承载力的计算。
关键词: 修正压力场理论 板柱节点 剪压区高度 临界斜裂缝倾角 冲切承载力
Calculation of punching shear capacity of RC slab-column connections without shear reinforcement
XIA Chengliang1,2, SHI Qingxuan1,2
, WANG Zhen1,2 1. Key Lab of Structural Engineering and Earthquake Resistance (Xi'an University of Architecture and Technology), Ministry of Education, Xi'an 710055, China;
2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
Abstract: In order to predict the punching shear capacity of slab-column connections more accurately, a new calculation method for punching shear capacity of slab-column connections was proposed based on the beam shear failure mechanism and modified compression-field theory (MCFT). Firstly, it was assumed that the punching load of reinforced concrete (RC) slab-column connections without shear reinforcement was jointly provided by the concrete in the upper shear compression zone, the aggregate interlock force in the cable-stayed zone, and the dowel action in the tension zone. Secondly, the different stress states of shear compression zone, cable-stayed zone, and tension zone were analyzed, and the shear bearing capacity calculation formulas of shear compression zone, cable-stayed zone, and tension zone were established respectively. Then, through statistical analysis and theoretical derivation, the calculation formulas of the heights of shear compression zone and compression zone, as well as the critical inclined crack angle were obtained. Finally, the contributions of the two parts of the punching resistance capacity were superimposed to establish the calculation method of punching shear capacity of RC slab-column connections without shear reinforcement. The calculation method was applied to predict the ultimate punching shear strength of 54 slab-column connections in relevant literature. Results show that the calculated values were in good agreement with the experimental values, and the variation coefficient was small. The proposed calculation method can be used to calculate the ultimate punching shear strength of RC slab-column connections without shear reinforcement.
Keywords: modified compression-field theory slab-column connection shear compression zone height critical inclined crack angle punching shear strength
板柱结构是一种以板和柱作为主要承重构件的结构体系，又称为无梁楼盖结构体系。该结构具有空间布置灵活，传力路径明确，结构层高较低，施工速度快等特点。以往的研究表明，板柱结构具有相对较低的抗弯刚度，在节点区域容易发生冲切破坏。由于在冲切破坏前板柱节点处于复杂的三维受力状态，剪力传递机制不明确，国内外对板柱节点冲切破坏的机理一直没有得出统一的结论，板柱节点的受冲切承载力计算方法大多都是基于简支板冲切试验提出的经验公式。
为完善无抗冲切钢筋的RC板柱节点的受冲切承载力计算方法，国内外学者进行了大量试验研究及理论分析。文献[1]对高强混凝土板柱节点的试验研究表明混凝土强度与节点受冲切承载力存在非线性关系。文献[2]考虑混凝土强度、钢筋的销栓作用影响对锥壳模型进行修正，通过对节点脱离扇形体建立平衡条件，推导了无抗冲切钢筋的RC板柱节点受冲切承载力计算式。文献[3]通过试验证明冲切破坏是节点区塑性转动使临界裂缝宽度增加导致，考虑截面高度，纵筋配筋率，骨料粒径、冲跨比等影响因素，推导出基于临界斜裂缝理论的无抗冲切钢筋的RC板柱节点受冲切承载力计算式。
本文认为板柱节点冲切破坏是由于板上部剪压区混凝土受压破坏和临界斜裂缝区域钢筋混凝土剪切失效共同导致。剪压区是临界斜裂缝未穿过的区域，其抗剪承载力由混凝土的抗压强度提供。临界斜裂缝区域的抗剪贡献则由混凝土间的骨料咬合力以及钢筋的销栓作用提供。本文使用修正压力场理论(MCFT)[4]计算无抗冲切钢筋的RC板柱节点临界斜裂缝区域的抗剪承载力，剪压区混凝土的抗剪承载力则在确定的剪压区范围内建立其计算表达式。通过对板柱节点冲切试验结果的验算, 验证了本计算方法的正确性，为板柱节点受冲切承载力的计算提供理论依据。
1 冲切破坏机理及破坏模型对以往无抗冲切钢筋的RC板柱节点冲切试验的破坏面观察发现，在板和柱相交的位置存在混凝土局部压碎的情况。因此本文认为无抗冲切钢筋的RC板柱节点冲切破坏类似于梁剪压破坏，临界斜裂缝发展到一定程度后，将被剪压区混凝土阻断，存在明显的受压区与受拉区。由于板柱节点冲切破坏属于三维剪切破坏，假定冲切荷载由剪压区未开裂混凝土和临界斜裂缝区域(包括斜拉区和受拉区)的骨料咬合力及销栓作用共同承担。
基于以上破坏机理，采用图 1(a)所示的分析模型，分别计算剪压区和临界斜裂缝区域(包括斜拉区和受拉区)的抗剪贡献。考虑如图 1(b)所示的冲切破坏锥，假定剪压区作用范围为与柱同宽的矩形区域，图 1(a)所示梯形剖面A′A1B1B′为图 1(b)中冲切破坏锥在竖直平面内的投影。
Fig. 1
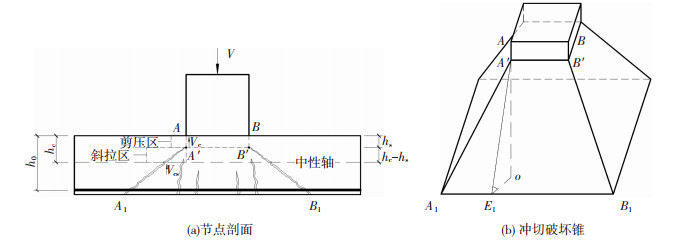图 1 冲切破坏模型 Fig. 1 Punching shear failure model 无抗冲切钢筋的RC板柱节点的极限冲切承载力由受压区的承载力垂直分量和临界斜裂缝区域骨料咬合力组成：
$V_{\mathrm{u}}=V_{\mathrm{c}}+V_{\mathrm{cs}}$ (1)
本文中剪压区混凝土提供的抗剪承载力Vc由文献[5]提出的分析方法建立计算表达式。临界斜裂缝区域混凝土提供的抗剪承载力Vcs基于修正压力场理论(MCFT)，不考虑抗弯钢筋的销栓力，通过迭代计算得到。
2 剪压区混凝土受冲切承载力计算参考文献[5]研究梁剪切失效的方法，本文将节点区分割成临界斜裂缝隔离体Ⅰ和与柱面接触的棱柱体Ⅱ，不考虑柱面对直接接触的棱柱体Ⅱ的影响，分别建立隔离体平衡条件，如图 2所示，得到剪压区高度表达式：
$\frac{h_{\mathrm{s}}}{h_{0}}=\frac{1+0.27 \tan ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{2}-\theta\right)}{1+\tan ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{2}-\theta\right)} \frac{h_{\mathrm{c}}}{h_{0}}$ (2)
Fig. 2
图 2 作用在节点单元上的力 Fig. 2 Force on elements of slab-column connection 式中：hs为剪压区高度，hc为受压区高度，h0为板有效高度，θ为临界斜裂缝倾角。
受压区高度由下式确定，取正根[5]：
$\left(\frac{h_{\mathrm{c}}}{h_{0}}\right)^{2}+600 \frac{\rho}{f_{\mathrm{c}}^{\prime}} \frac{h_{\mathrm{c}}}{h_{0}}-600 \frac{\rho}{f_{\mathrm{c}}^{\prime}}=0$ (3)
式中：f′c为混凝土圆柱体抗压强度，ρ为板受弯钢筋配筋率。
在极限状态下，假定受压区混凝土压应力σz符合抛物线分布规律且应变分布为倒三角形，并且压应力σz在混凝土受压区最外边缘处达到混凝土抗压强度f′c，则从受拉钢筋中心至中性轴z处的混凝土纵向正应力σz可按式(4)计算[6]：
$\sigma_{\mathrm{z}}=f_{\mathrm{c}}^{\prime}\left[2\left(\frac{z}{h_{\mathrm{c}}}\right)-\left(\frac{z}{h_{\mathrm{c}}}\right)^{2}\right]$ (4)
在剪压区高度hs范围内对混凝土压应力σz积分，得到剪压区混凝土的受剪承载力Vc贡献表达式：
$V_{\mathrm{c}}=c \int_{h_{\mathrm{c}}-h_{\mathrm{s}}}^{h_{\mathrm{c}}} \sqrt{f_{\mathrm{c}}^{\prime}\left(f_{\mathrm{c}}^{\prime}-\sigma_{\mathrm{z}}\right)} \mathrm{d} z=0.5 f_{\mathrm{c}}^{\prime} c h_{\mathrm{c}}\left(\frac{h_{\mathrm{s}}}{h_{\mathrm{c}}}\right)^{2}$ (5)
式中c为柱截面尺寸。
3 修正压力场理论(MCFT)修正压力场理论(MCFT)[4]是由加拿大学者Vecchio和Collins采用非线性混凝土本构，通过对开裂混凝土单元建立平衡方程和相容方程，提出的一种计算正交双向承受薄膜应力的钢筋混凝土平面单元受剪承载力的方法。随着荷载持续增大，节点区形成临界斜裂缝并发展到受压区，在裂缝处正应力与剪应力的共同作用下节点发生冲切破坏。本文在修正压力场理论的基础上推导无抗冲切钢筋的RC板柱节点临界斜裂缝区域的受冲切承载力。
3.1 MCFT应变协调条件根据修正压力场理论(MCFT)[4]中钢筋与混凝土完全黏结的假定及应变莫尔圆理论，可得到开裂混凝土单元的应变协调条件：
$\varepsilon_{\mathrm{x}}=\varepsilon_{\mathrm{cx}}=\varepsilon_{\mathrm{sx}}$ (6)
$\varepsilon_{\mathrm{y}}=\varepsilon_{\mathrm{cy}}=\varepsilon_{\mathrm{sy}}$ (7)
$\varepsilon_{\mathrm{x}}+\varepsilon_{\mathrm{y}}=\varepsilon_{1}+\varepsilon_{2}$ (8)
$\tan ^{2} \theta=\frac{\varepsilon_{\mathrm{x}}-\varepsilon_{2}}{\varepsilon_{1}-\varepsilon_{\mathrm{x}}}$ (9)
式中：ε1、ε2分别为垂直于裂缝的平均主拉应变和平均主压应变，εx、εy分别为平均横向应变和平均纵向应变，εcx、εcy分别为混凝土横向应变和纵向应变，εsx、εsy为分别为横向钢筋应变和纵向钢筋应变。
3.2 MCFT平衡条件将修正压力场理论(MCFT)[4]中的钢筋单元和开裂混凝土单元叠加得到图 3(a)所示的开裂钢筋混凝土单元的应力状态。根据图 3(a)所示的开裂钢筋混凝土单元的应力状态和图 3(b)所示的混凝土平均应力莫尔圆，可得到平衡条件：
$\tau=\tau_{\mathrm{cxy}}$ (10)
$\sigma_{\mathrm{cx}}=\sigma_{\mathrm{c} 1}-\tau_{\mathrm{cxy}} / \tan \theta$ (11)
$\sigma_{\mathrm{cy}}=\sigma_{\mathrm{c} 1}-\tau_{\mathrm{cxy}} \tan \theta$ (12)
$\sigma_{\mathrm{c} 2}=\sigma_{\mathrm{c} 1}-\tau_{\mathrm{cxy}}(\tan \theta+\cot \theta)$ (13)
Fig. 3
图 3 开裂钢筋混凝土应力状态与混凝土平均应力莫尔圆 Fig. 3 Stress state of cracked reinforced concrete and Mohr's circle for average stress of concrete 式中：σc1、σc2分别为开裂混凝土的主拉应力和主压应力，σcx、σcy分别为混凝土在x和y方向上的平均应力，τ为开裂钢筋混凝土单元的剪应力，τcxy为开裂混凝土单元的平均剪应力。
修正压力场理论(MCFT)[4]认为裂缝引起的局部应力对开裂混凝土单元的极限承载力有重要影响。考虑裂缝之间的局部应力可得到混凝土单元在裂缝处及裂缝间的平衡方程：
$\sigma_{\mathrm{sxcr}}=\left(\sigma_{\mathrm{c} 1}+\tau_{\mathrm{ci}} \cot \theta+\sigma_{\mathrm{sx}}\right) \rho_{\mathrm{sx}}$ (14)
$\sigma_{\mathrm{sycr}}=\left(\sigma_{\mathrm{c} 1}-\tau_{\mathrm{ci}} \tan \theta+\sigma_{\mathrm{sy}}\right) \rho_{\mathrm{sy}}$ (15)
式中：τci为裂缝表面的剪应力，σsxcr、σsycr分别为裂缝处的横向钢筋和纵向钢筋的应力，σsx、σsy分别为裂缝间横向钢筋和纵向钢筋的平均拉应力，ρsx、ρsy分别为横向钢筋和纵向钢筋的配筋率。
3.3 开裂混凝土本构关系 3.3.1 混凝土本构由于在拉-压双轴应力状态下的混凝土比标准圆柱体混凝土强度更低、更脆，因此修正压力场理论(MCFT)[4]采用考虑混凝土软化现象的混凝土受压应力-应变关系：
$\sigma_{\mathrm{c} 2} =f_{\mathrm{c} 2 \max }\left[2\left(\frac{\varepsilon_{2}}{\varepsilon_{\mathrm{c}}^{\prime}}\right)-\left(\frac{\varepsilon_{2}}{\varepsilon_{\mathrm{c}}^{\prime}}\right)^{2}\right] $ (16)
$\frac{f_{\mathrm{c} 2 \max }}{f_{\mathrm{c}}^{\prime}} =\frac{1}{0.8-0.34\left(\varepsilon_{1} / \varepsilon_{\mathrm{c}}^{\prime}\right)} \leqslant 1$ (17)
受拉应力-应变关系为：
当ε1≤εcr时：
$\sigma_{\mathrm{c} 1}=E_{\mathrm{c}} \varepsilon_{1}$ (18)
当ε1＞εcr时：
$\sigma_{\mathrm{c} 1}=\frac{0.33 \sqrt{f_{\mathrm{c}}^{\prime}}}{1+\sqrt{500 \varepsilon_{1}}}$ (19)
式中：Ec为混凝土弹性模量，ε′c为混凝土峰值压应变，εcr为混凝土开裂应变，fc2max为混凝土受压方向上的极限压应力。
3.3.2 钢筋本构修正压力场理论(MCFT)[4]假定钢筋轴向应力仅取决于轴向应变参数，并假定垂直于钢筋截面的剪应力为零，其应力-应变关系采用理想弹塑性模型：
$\sigma_{\mathrm{sx}}=E_{\mathrm{s}} \varepsilon_{\mathrm{sx}} \leqslant f_{\mathrm{sy}}$ (20)
式中：Es为板内纵筋弹性模量，εsx为钢筋应变，fsy为板内纵筋屈服强度。
4 无抗冲切钢筋RC板冲切承载力计算 4.1 计算方法与步骤修正压力场理论(MCFT)[4]假定混凝土开裂后拉应力仍参与抗剪，由图 4所示的无抗冲切钢筋的RC板开裂后的内力平衡可知，在两条裂缝间的混凝土拉应力达到最大值。选取临界斜裂缝与竖向平面截取的棱柱体作为分析对象，棱柱体应力分布与开裂RC板相同，通过对柱面与棱柱体相互接触的平面上的应力积分来计算板的极限承载力。假定柱面与棱柱体相互接触的平面上的剪应力均匀分布，则单块棱柱体的冲切破坏截面的剪应力τ为：
$\tau=\frac{V_{\mathrm{cs} 1}}{\frac{1}{2}\left[c+c+2\left(h-h_{\mathrm{s}}\right) \cot \theta\right]\left(h-h_{\mathrm{s}}\right)}$ (21)
Fig. 4
图 4 受剪混凝土的主应力 Fig. 4 Principal stress diagram of shear concrete 式中：h为板厚，Vcs1为单块棱柱体承受的剪力。
通过建立棱柱体在水平方向上的力的平衡条件可得:
$\varepsilon_{\mathrm{x}}=\left(\sigma_{\mathrm{c} 2} \cos ^{2} \theta-\sigma_{\mathrm{c} 1} \sin ^{2} \theta\right) /\left(\rho_{\mathrm{sx}} E_{\mathrm{s}}\right)$ (22)
根据修正压力场理论，当板未布置抗冲切钢筋时, 裂缝处的平均应力平衡关系见图 5(a)，临界斜裂缝上存在钢筋拉应力σsx和混凝土主拉应力σc1；两条裂缝间的应力平衡关系见图 5(b)，存在局部剪应力τci和局部压应力σci，其中局部压应力σci很小，可以忽略不计。在给定外力作用下，这两组应力状态应该是应力等效的。因此可得到：
$\sigma_{\mathrm{c} 1} \sin \theta+\rho_{\mathrm{sx}} \sigma_{\mathrm{sx}} \sin \theta=\rho_{\mathrm{sx}} \sigma_{\mathrm{sxcr}} \sin \theta-\tau_{\mathrm{ci}} \cos \theta$ (23)
$\sigma_{\mathrm{c1}} \cos \theta=\tau_{\mathrm{ci}} \sin \theta$ (24)
Fig. 5
图 5 计算平均应力与裂缝处的局部应力 Fig. 5 Calculated average stress and local stress at a crack 由式(23)可得，未配置抗冲切钢筋的RC板柱节点冲切破坏时的最大主拉应力:
$\sigma_{\mathrm{c} 1 \max }=\tau_{\mathrm{ci}} \tan \theta$ (25)
对于无抗冲切钢筋的RC板柱节点，联立式(10)、式(12)和式(25)可得:
$\tau=\tau_{\mathrm{ci}}$ (26)
基于文献[4]对混凝土裂缝截面骨料咬合力的研究，当局部压应力σci很小时，可得到局部剪应力表达式:
$\tau_{\mathrm{ci}}=\frac{0.18 \sqrt{f_{\mathrm{c}}^{\prime}}}{0.31+24 w /\left(a_{\mathrm{g}}+16\right)}$ (27)
式中：ag为混凝土材料的最大骨料粒径，ag通常可取为20 mm，w为钢筋混凝土开裂单元的平均裂缝宽度，当不配置抗冲切钢筋时，可由下式计算:
$w=\varepsilon_{1} \frac{S_{\mathrm{mx}}}{\sin \theta}$ (28)
式中：Smx为垂直于x方向的裂缝间距，当钢筋混凝土板在板顶、板底布置双层钢筋网时，Smx为抗弯钢筋在垂直方向上的间距；根据文献[7]的研究，Smx可近似取0.9h0。
临界斜裂缝倾角θ是确定冲切锥几何形状和冲切承载力的重要参数，文献[8]通过线性拟合得到了倾角θ与抗弯钢筋配筋特征值ρsfy/fc的相关性表达式。本文通过对以往试验数据的统计分析，发现倾角θ和柱截面周长与板有效厚度之比Cc/h0及ρsfy/fc显著相关。因此，本文认为影响节点临界斜裂缝倾角θ的因素主要为Cc/h0和ρsfy/fc，假定θ由以下方程式表达：
$\theta=a\left(C_{\mathrm{c}} / h_{0}\right)^{\alpha}\left(\rho_{\mathrm{s}} f_{\mathrm{y}} / f_{\mathrm{c}}\right)^{\beta}$ (29)
为了确定待定系数α和β，采用文献[9]中的分析方法，分别检验单一变量对临界斜裂缝倾角θ的影响，可以得到单一变量影响系数(α和β)变化过程中对临界斜裂缝倾角平均偏差e的变化规律，如图 6所示。由图可知，α和β与临界斜裂缝倾角平均偏差e呈明显非线性关系，存在某一极值点使e达到最小值。由分析结果确定待定系数后，可得到倾角θ的最终表达式：
$\theta=32\left(C_{\mathrm{c}} / h_{0}\right)^{-0.12}\left(\rho_{\mathrm{s}} f_{\mathrm{y}} / f_{\mathrm{c}}\right)^{-0.08}$ (30)
Fig. 6
图 6 样本平均偏差-影响因数曲线 Fig. 6 Sample average deviation-influence parameter curve 将上述公式计算的倾角与试验值对比，本文拟合公式均值为1.09，变异系数为0.20；文献[8]拟合公式均值为1.13，变异系数为0.20。通过表 1中试验值与计算值对比可知，本文拟合的公式不受文献[8]中35°上限角的限制，且对除方形柱以外的其他柱截面形状的节点预测结果较好。因此，本文拟合的角度计算公式能较好预测冲切斜裂缝倾角。
表 1
表 1 冲切裂缝倾角试验值与计算值对比 Tab. 1 Comparison of experimental and calculated punching inclined crack angles 文献 试件编号 fc/MPa 柱头形状 有效板厚h0/mm 纵向配筋率ρs/% fy/MPa Cc/ h0 ρs fy/ fc θ/(°) θcal/(°) 文献[8] θ/(°) 文献[1] HSC6 108.80 圆形 201 0.60 633.0 3.91 0.035 39.6 35.54 34.30
HSC9 84.10 圆形 202 0.33 634.0 3.89 0.025 35.4 36.54 34.50
文献[10] SH2 21.20 矩形 150 1.28 453.6 6.67 0.274 31.3 28.27 29.52
SH4 23.48 矩形 150 1.28 453.6 6.67 0.247 28.9 28.50 30.05
SHH 23.33 六边形 150 1.28 453.6 6.40 0.249 28.1 28.62 30.02
SHC 21.13 圆形 150 1.28 453.6 6.28 0.275 26.0 28.46 29.50
SL2 21.43 矩形 150 0.86 453.6 6.67 0.182 22.5 29.21 31.36
SL4 21.74 矩形 150 0.86 453.6 6.67 0.179 26.8 29.24 31.41
SLH 21.13 六边形 150 0.86 453.6 6.40 0.185 28.6 29.32 31.31
SLC 22.57 圆形 150 0.86 453.6 6.28 0.173 30.6 29.54 31.54
注：Cc为柱截面周长。
表 1 冲切裂缝倾角试验值与计算值对比 Tab. 1 Comparison of experimental and calculated punching inclined crack angles
由式(20)、(26)、(27)可得，无抗冲切钢筋的RC板柱节点在x方向上的抗冲切承载力为
$\begin{aligned}V_{\mathrm{csx}} &=\frac{1}{2} \times \frac{0.36 \sqrt{f_{\mathrm{c}}^{\prime}}}{0.31+24 w /\left(a_{\mathrm{g}}+16\right)} \times \\& {\left[2 c+2\left(h-h_{\mathrm{s}}\right) \cot \theta\right]\left(h-h_{\mathrm{s}}\right) }\end{aligned}$ (31)
将式(5)和式(31)代入式(1)得到节点抗冲切承载力
$\begin{aligned}V_{\mathrm{u}}=& 2 f_{\mathrm{c}}^{\prime} c h_{\mathrm{c}}\left(\frac{h_{\mathrm{s}}}{h_{\mathrm{c}}}\right)^{2}+\frac{0.36 \sqrt{f_{\mathrm{c}}^{\prime}}}{0.31+24 w /\left(a_{\mathrm{g}}+16\right)} \times \\& {\left[2 c+2\left(h-h_{\mathrm{s}}\right) \cot \theta\right]\left(h-h_{\mathrm{s}}\right) }\end{aligned}$ (32)
节点受冲切承载力计算流程见图 7。
Fig. 7
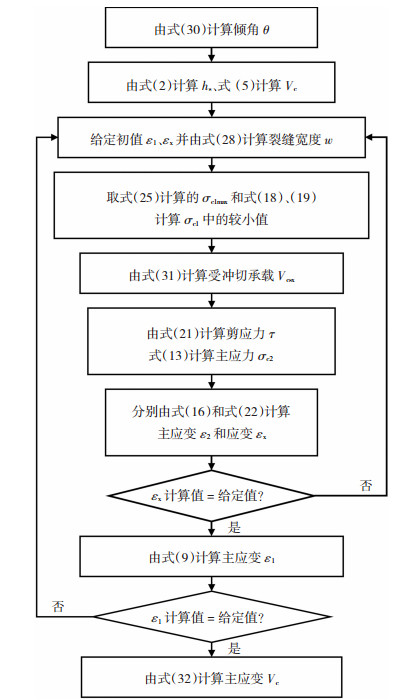图 7 节点受冲切承载力计算流程 Fig. 7 Flow chart of punching shear strength 4.2 计算结果与试验值对比为验证本文提出的冲切承载力计算方法的准确性与适用性，采用式(32)对相关文献中54个[1-2, 8, 10-21]无抗冲切钢筋的RC板柱节点在竖向荷载作用下的抗冲切试验结果进行验算。节点试验的混凝土立方体抗压强度变化范围为27.5~124.87 MPa，柱截面尺寸变化范围为130~520 mm, 冲跨比λ变化范围为2.83~7.13，纵筋配筋率ρs变化范围为0.33%~1.73%，节点支承方式均为板四边简支，收集的试验数据具有一定的代表性。图 8(a)为文献[21]的理论公式计算结果与试验值对比。图 8(b)为本文公式(32)的计算结果与试验值对比。由图可知，文献[21]的计算值与试验值比值的平均值、标准差、变异系数分别为0.771、0.147、0.191；本文提出的计算方法的计算值与试验值比值的平均值、标准差、变异系数分别为1.005、0.163、0.162。通过对比可知，采用本文提出的方法计算出的节点抗冲切承载力与试验值较为接近，并且具有较小的标准差和变异系数，表明本文提出的无抗冲切钢筋的RC板柱节点冲切承载力计算方法较为合理。
Fig. 8
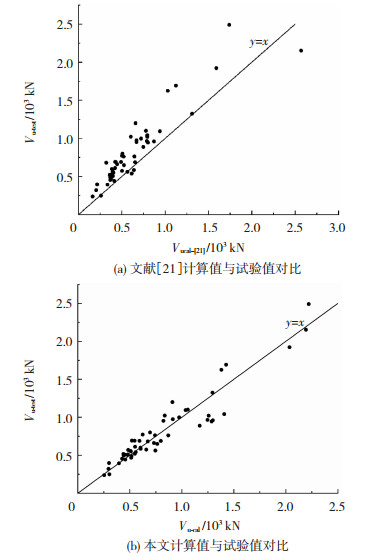图 8 计算值与试验值对比 Fig. 8 Comparison of experimental and calculated results 5 结论1) 本文通过对大量板柱节点冲切裂缝倾角试验数据的总结，对影响冲切裂缝倾角的因素进行统计分析，得到临界斜裂缝倾角θ和柱截面周长与板有效厚度之比Cc/h0及抗弯钢筋配筋率特征值ρsfy/fc之间的相关性表达式。通过对文献中冲切斜裂缝倾角的验算，证明该关系式能较准确的预测无抗冲切钢筋的RC板柱节点的冲切斜裂缝倾角。
2) 将无抗冲切钢筋的RC板柱节点的冲切破坏模式类比梁的剪压破坏，结合修正压力场理论(MCFT)，分析板柱节点剪压区与临界斜裂缝区域(包括斜拉区和受拉区)不同的受力状态，推导无抗冲切钢筋的RC板柱节点的受冲切承载力计算式，分别计算剪压区与临界斜裂缝区域的冲切承载力贡献。通过对文献中大量试验结果的验算，以及与文献中冲切承载力计算值的比较，验证了本文提出的计算方法的准确性及适用性。
参考文献
[1] HALLGREN M. Punching shear capacity of reinforced high strength concrete slabs[D]. Stockholm: KTH Royal Institute of Technology, 1996: 77
[2] MARZOUK H, HUSSEIN A. Punching shear analysis of reinforced high-strength concrete slabs[J]. Canadian Journal of Civil Engineering, 1991, 18(6): 955. DOI:10.1139/l91-118
[3] MUTTONI A, RUIZ M F. Shear strength of members without transverse reinforcement as function of critical shear crack width[J]. ACI Structural Journal, 2008, 105(2): 163. DOI:10.1016/j.jhazmat.2007.12.050
[4] VECCHIO J F, COLLINS P M. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Journal, 1986, 83(2): 219.
[5] ZARARIS P D. Shear compression failure in reinforced concrete deep beams[J]. Journal of Structural Engineering, 2003, 29(4): 548. DOI:10.1061/(asce)0733-9445(2003)129:4(544)
[6] 混凝土结构设计规范: GB 50010—2010 [S]. 北京: 中国建筑工业出版社, 2010
Code for design of concrete structures: GB 50010—2010 [S]. Beijing: China Architecture & Building Press, 2010
[7] 魏巍巍. 基于修正压力场理论的钢筋混凝土结构受剪承载力及变形研究[D]. 大连: 大连理工大学, 2011: 78
WEI Weiwei. Study on shear capacity and deformation for reinforced concrete structure based on modified compression field theory[D]. Dalian: Dalian University of Technology, 2011: 78
[8] 邓清. 板柱节点冲切受力性能及承载力计算方法研究[D]. 长沙: 湖南大学, 2018: 46
DENG Qing. Study on punching shear behavior and capacity of reinforced concrete slab-column connections[D]. Changsha: Hunan University, 2018: 46
[9] TIMOSHENKO S, WOINOWSKYKRIEGER S. Theory of plate and shells[M]. New York: McGraehill, 1959: 8. DOI:10.1038/148606a0
[10] 邹品增. 柱截面形状对板柱节点受冲切性能影响的试验研究[D]. 长沙: 湖南大学, 2015: 22
ZOU Pinzeng. Experimental study on column section shape role in punching shear performance of slab-column connection[D]. Changsha: Hunan University, 2015: 22
[11] 刘立渠. 钢筋混凝土板考虑加载面积边长比及纵筋影响的抗冲切试验研究[D]. 北京: 中国建筑科学研究院, 2006: 51
LIU Liqu. Experimental study on punching shear strength of RC slabs with the effect of column aspect ratios and flexural reinforcement ratios[D]. Beijing: China Academy of Building Research, 2006: 51
[12] GLIKMAN M. Inclined shear reinforcement in reinforced concrete slab-column connections[D]. Austin: The University of Texas at Austin, 2016: 39
[13] RUIZ M F, MUTTONI A, KUNZ J. Strengthening of flat slabs against punching shear using post-installed shear reinforcement[J]. ACI Structural Journal, 2010, 107(4): 436. DOI:10.4359/51663816
[14] LIPS S, RUIZ M F, MUTTONI A. Experimental investigation on punching strength and deformation capacity of shear-reinforced slabs[J]. ACI Structural Journal, 2012, 109(6): 897.
[15] CANTONE R, RUIZ M F, BUJNAK J, et al. Enhancing punching strength and deformation capacity of flat slabs[J]. ACI Structural Journal, 2019, 116(5): 272. DOI:10.14359/51716842
[16] PILAKOUTAS K, LI X. Alternative shear reinforcement for reinforced concrete flat slabs[J]. Journal of Structural Engineering, 2003, 129(9): 1167. DOI:10.1061/(asce)0733-9445(2003)129:9(1164)
[17] GUANDALINI S, BURDET L O, MUTTONI A. Punching tests of slabs with low reinforcement ratios[J]. ACI Structural Journal, 2009, 106(6): 92. DOI:10.1109/ICNSC.2009.4919362
[18] SCHMIDT P, KUERES D, HEGGER J. Punching shear behavior of reinforced concrete flat slabs with a varying amount of shear reinforcement[J]. Structural Concrete, 2018, 2. DOI:10.1002/suco.201900017
[19] 彭检. 钢筋混凝土板柱节点抗冲切试验研究[D]. 长沙: 湖南大学, 2013: 22
PENG Jian. Experimental study on punching shear failure of reinforced concrete slabs-column connections[D]. Changsha: Hunan University, 2013: 22
[20] HASSAN M, AHMED A E, BENMOKRANE B. Punching shear strength of glass fiber-reinforced polymer reinforced concrete flat slabs[J]. Canadian Journal of Civil Engineering, 2013, 40(10): 953. DOI:10.1139/cjce-2012-0177
[21] 史庆轩, 金渝林. 基于修正压力场理论的钢筋混凝土板抗冲切承载力计算[J]. 工业建筑, 2019, 49(6): 94.
SHI Qingxuan, JIN Yulin. Punching shear strength of RC slabs based on modified compression field theory[J]. Industrial Construction, 2019, 49(6): 94.
