郑良杰,马彪,陈漫,于亮,王亮
( 北京理工大学 机械与车辆学院, 北京 100081)
摘要:
为研究在不同花键摩擦因数下湿式多片离合器分离过程中的摩擦转矩和间隙变化,建立湿式多片离合器分离过程动力学数值模型,并提出不均匀系数以表征分离间隙均匀度。研究结果表明:分离过程中各摩擦副间隙首先缓慢增大,再迅速增大,剧烈波动之后趋于稳定；间隙稳定之后分离过程结束,而花键摩擦因数对分离过程持续时间几乎没有影响；不考虑花键摩擦时,各摩擦副均匀分离；考虑花键摩擦后,各摩擦副间隙从第一副至第六副依次减小,花键摩擦因数的增加显著恶化了分离间隙均匀度；分离过程的粗糙接触转矩初始值及其衰减速率随花键摩擦因数的增大而减小,分离过程末期的黏性转矩随花键摩擦因数的增大而增大。因此降低花键摩擦因数,有助于湿式多片离合器的均匀分离和降低带排转矩。
关键词: 湿式多片离合器 分离过程 花键摩擦因数 摩擦转矩 摩擦副间隙
DOI：10.11918/202107082
分类号:U463.211
文献标识码:A
基金项目:国家自然科学基金 (7,5).
Influence of spline friction coefficient on a wet multi-disc clutch in the disengaging process
ZHENG Liangjie,MA Biao,CHEN Man,YU Liang,WANG Liang
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)
Abstract:
To study the variations of friction torque and gaps during the disengaging process of a wet multi-disc clutch with different spline friction coefficients, a comprehensive disengaging dynamic model is proposed, and the non-uniformity coefficient is employed to characterize the disengaging uniformity. The results show that during the disengaging process, the friction pair gaps first increase slowly, then increase rapidly, finally stabilize after fluctuating. The disengaging process ends when the friction pair gaps stabilize, but the spline friction coefficient has slight effect on the disengaging time. When considering the spline friction, the disengaged gaps are no longer uniform, but decrease from the first friction pair to the sixth friction pair in sequence. Moreover, the increase of spline friction coefficient significantly deteriorates the disengaging uniformity. Finally, with the increase of spline friction coefficient, the initial value and change rate of contact torque decrease, while the final value of hydrodynamic torque increases. Therefore, the decrease of spline friction coefficient promotes the uniform disengaging of friction pairs and reduces the drag torque.
Key words: wet multi-disc clutch disengaging process spline friction coefficient friction torque friction pair gaps
郑良杰, 马彪, 陈漫, 于亮, 王亮. 花键摩擦对湿式多片离合器分离过程影响[J]. 哈尔滨工业大学学报, 2022, 54(7): 89-95. DOI: 10.11918/202107082.
ZHENG Liangjie, MA Biao, CHEN Man, YU Liang, WANG Liang. Influence of spline friction coefficient on a wet multi-disc clutch in the disengaging process[J]. Journal of Harbin Institute of Technology, 2022, 54(7): 89-95. DOI: 10.11918/202107082.
基金项目 国家自然科学基金(51975047，51775045) 作者简介 郑良杰(1995—)，男，博士研究生;
马彪(1964—)，男，教授，博士生导师 通信作者 于亮，yuliang@bit.edu.cn 文章历史 收稿日期: 2021-07-22
Abstract Full text Figures/Tables PDF
花键摩擦对湿式多片离合器分离过程影响
郑良杰, 马彪, 陈漫, 于亮
, 王亮 北京理工大学 机械与车辆学院，北京 100081
收稿日期: 2021-07-22
基金项目: 国家自然科学基金(51975047，51775045)
作者简介: 郑良杰(1995—)，男，博士研究生; 马彪(1964—)，男，教授，博士生导师
通信作者: 于亮，yuliang@bit.edu.cn
摘要: 为研究在不同花键摩擦因数下湿式多片离合器分离过程中的摩擦转矩和间隙变化，建立湿式多片离合器分离过程动力学数值模型，并提出不均匀系数以表征分离间隙均匀度。研究结果表明: 分离过程中各摩擦副间隙首先缓慢增大，再迅速增大，剧烈波动之后趋于稳定；间隙稳定之后分离过程结束，而花键摩擦因数对分离过程持续时间几乎没有影响；不考虑花键摩擦时，各摩擦副均匀分离；考虑花键摩擦后，各摩擦副间隙从第一副至第六副依次减小，花键摩擦因数的增加显著恶化了分离间隙均匀度；分离过程的粗糙接触转矩初始值及其衰减速率随花键摩擦因数的增大而减小，分离过程末期的黏性转矩随花键摩擦因数的增大而增大。因此降低花键摩擦因数，有助于湿式多片离合器的均匀分离和降低带排转矩。
关键词: 湿式多片离合器 分离过程 花键摩擦因数 摩擦转矩 摩擦副间隙
Influence of spline friction coefficient on a wet multi-disc clutch in the disengaging process
ZHENG Liangjie, MA Biao, CHEN Man, YU Liang
, WANG Liang School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China
Abstract: To study the variations of friction torque and gaps during the disengaging process of a wet multi-disc clutch with different spline friction coefficients, a comprehensive disengaging dynamic model is proposed, and the non-uniformity coefficient is employed to characterize the disengaging uniformity. The results show that during the disengaging process, the friction pair gaps first increase slowly, then increase rapidly, finally stabilize after fluctuating. The disengaging process ends when the friction pair gaps stabilize, but the spline friction coefficient has slight effect on the disengaging time. When considering the spline friction, the disengaged gaps are no longer uniform, but decrease from the first friction pair to the sixth friction pair in sequence. Moreover, the increase of spline friction coefficient significantly deteriorates the disengaging uniformity. Finally, with the increase of spline friction coefficient, the initial value and change rate of contact torque decrease, while the final value of hydrodynamic torque increases. Therefore, the decrease of spline friction coefficient promotes the uniform disengaging of friction pairs and reduces the drag torque.
Keywords: wet multi-disc clutch disengaging process spline friction coefficient friction torque friction pair gaps
湿式多片离合器是车辆传动系统功率传递和速度切换的重要部件，决定着传动装置工作可靠性和使用寿命。目前，国内外学者对湿式多片离合器的研究多集中于接合过程摩擦转矩和分离状态带排转矩。学者们主要从离合器工作参数、结构参数等方面研究了接合过程中的摩擦转矩特征。马彪等[1]、Yu等[2-3]建立了湿式离合器多场耦合数值模型，研究了工作参数对摩擦转矩产生和变化的影响规律。Jang等[4-5]、Li等[6]基于热机耦合的流体动力学模型研究了摩擦元件沟槽特征对离合器接合过程的温度场和摩擦转矩变化的影响规律。吴健鹏等[7]研究了湿式离合器加速寿命过程的摩擦副温升变化特性。考虑摩擦元件的结构特征，何松[8]建立了摩擦元件花键齿受力模型，于亮等[9]、张恒等[10]研究了花键摩擦力导致的多片离合器轴向平均比压和摩擦转矩衰减特性。离合器处于分离状态时，摩擦副间润滑油的黏性剪切将产生带排转矩，导致传动效率的降低。Iqbal等[11]、Hu等[12]分别对中低速和高速带排转矩进行了理论研究，并建立了相应的数值计算模型。Wu等[13]对径向槽单摩擦副的油液两相流进行了可视化试验研究。师路骐等[14]研究了摩擦元件偏置和间隙收缩对带排转矩的影响。Wang等[15]通过建立数学统计模型，研究了摩擦副间隙分布对低速带排转矩的影响，间隙分布越不均匀，带排转矩越大。更为严重的是分离过程中甚至会出现某些摩擦副无法分离的情况，带来摩擦副的长时滑摩，造成离合器烧蚀。分离过程持续时间和分离过程转矩变化对车辆换挡的精确控制非常关键。然而，目前缺乏针对湿式多片离合器分离过程的相关研究。
针对以上问题，本文考虑摩擦元件的结构特征，建立了湿式多片离合器分离过程动力学数值模型，研究了不同花键摩擦因数下的六摩擦副湿式离合器的动态分离过程，获得了分离过程摩擦副间隙的变化规律，提出了不均匀系数以表征湿式多片离合器分离间隙均匀度。
1 数值模型在分离过程的初始时刻，湿式多片离合器仍然保持接合状态，因此需要建立离合器全工作过程的仿真模型。如图 1所示，在离合器接合或分离过程中，可以轴向移动的摩擦元件有活塞、摩擦片和钢片，其轴向受力如图 2所示。假设在分离过程中，离合器温度保持恒定。
Fig. 1
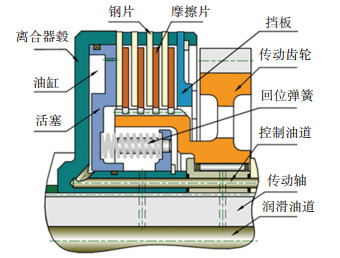图 1 湿式多片离合器结构图 Fig. 1 Structure of wet multi-disc clutch Fig. 2
图 2 摩擦元件轴向受力示意图 Fig. 2 Axial force analysis of friction components 1.1 轴向运动模型对于摩擦副为Z的湿式多片离合器，将摩擦元件按照从活塞至最后一片摩擦片的顺序编号为0、1、2、3、…、Z-1和Z。相邻摩擦元件之间的间隙可以表示为
$\left\{\begin{array}{l}\delta_{0}=x_{0}-x_{1}-H_{\mathrm{sd}} \\\delta_{1}=x_{1}-x_{2}-H_{\mathrm{fd}} \\\delta_{2}=x_{2}-x_{3}-H_{\mathrm{sd}} \\\ \ \vdots \\\delta_{Z-1}=x_{Z-1}-x_{Z}-H_{\mathrm{fd}} \\\delta_{Z}=x_{Z}\end{array}\right.$ (1)
式中：x为各摩擦元件位移，Hsd为钢片厚度，Hfd为摩擦片厚度。
各摩擦元件的受力平衡方程为
$\left\{\begin{array}{l}F_{\mathrm{v} 0}+F_{\mathrm{c} 0}+F_{\mathrm{k}}-F_{\mathrm{p}}-F_{\mathrm{d} 0}-F_{\mathrm{impact}}=m_{0} \ddot{x}_{0} \\F_{\mathrm{v} 1}+F_{\mathrm{c} 1}-F_{\mathrm{v} 0}-F_{\mathrm{c} 0}-F_{\mathrm{d} 1}-F_{\mathrm{s} 1}=m_{1} \ddot{x}_{1} \\F_{\mathrm{v} 2}+F_{\mathrm{c} 2}-F_{\mathrm{v} 1}-F_{\mathrm{c} 1}-F_{\mathrm{f} 2}=m_{2} \ddot{x}_{2} \\\ \ \vdots \\F_{\mathrm{v}(Z-1)}+F_{\mathrm{c}(Z-1)}-F_{\mathrm{v}(Z-2)}-F_{\mathrm{c}(Z-2)}-F_{\mathrm{d}(Z-1)}- \\\ \ \ \ \ \ \ \ \ \ \ \ F_{\mathrm{s}(Z-1)}=m_{1} \ddot{x}_{(Z-1)} \\F_{\mathrm{v} Z}+F_{\mathrm{c} Z}-F_{\mathrm{v}(Z-1)}-F_{\mathrm{c}(Z-1)}-F_{\mathrm{f} Z}=m_{2} \ddot{x}_{Z}\end{array}\right.$ (2)
式中：Fv为流体动压承载力，Fc为微凸体粗糙接触力，Fk为回位弹簧作用力，Fp为控制油压作用力，Fd为阻尼力，Fimpact为活塞与离合器毂的碰撞接触力，Fs和Ff分别为钢片和摩擦片的花键摩擦力，m0、m1和m2分别为活塞、钢片和摩擦片质量，
1.2 流体润滑模型基于平均层流假设，并考虑摩擦材料的渗透性和粗糙接触效应[16-17]，假设各摩擦元件始终平行，油膜压力轴对称，边界油膜压力为零，得到柱坐标系下的平均油膜压力表达式为
$\begin{array}{l}\bar{p}=\frac{B}{4 A}\left(r^{2}-R_{\mathrm{o}}^{2}\right)+\frac{3 \eta}{A} \frac{\partial \bar{h}_{\mathrm{T}}}{\partial t}\left(r^{2}-R_{\mathrm{o}}^{2}\right)+ \\\ \ \ \ \ \ \ \ \ln \frac{r}{R_{\mathrm{o}}}\left(\frac{B}{4 A}+\frac{3 \eta}{A} \frac{\partial \bar{h}_{\mathrm{T}}}{\partial t}\right) \frac{R_{\mathrm{o}}^{2}-R_{\mathrm{i}}^{2}}{\ln R_{\mathrm{i}}-\ln R_{\mathrm{o}}}\end{array}$ (3)
式中：Ri和Ro分别为摩擦副内外半径，η为润滑油动力黏度，hT为平均油膜厚度，系数A和B分别为：
$A=\phi_{r} h^{3}+12 \varPsi d_{\mathrm{m}}$ (4)
$B=\phi_{r} \rho h^{3}\left(3 \omega_{\mathrm{f} 1}^{2}+4 \omega_{\mathrm{f1}} \omega_{\mathrm{f} 2}+3 \omega_{\mathrm{f} 2}^{2}\right) / 5$ (5)
式中：?r为径向压力流量因子，h为名义油膜厚度，Ψ和dm分别为摩擦材料的渗透率和厚度，ρ为润滑油密度，ωf1和ωf2分别为钢片和摩擦片的角速度。
考虑到活塞与第一片钢片以相同的角速度旋转，并且同为钢材料，对公式(3)进行简化，得到活塞与第一片钢片之间的平均油膜压力为
$\begin{gathered}\bar{p}=\frac{1}{2} \rho \omega_{\mathrm{f} 1}^{2}\left(r^{2}-R_{\mathrm{o}}^{2}\right)+\frac{3 \eta}{\phi_{r} h^{3}} \frac{\partial \bar{h}_{\mathrm{T}}}{\partial t}\left(r^{2}-R_{\mathrm{o}}^{2}\right)+ \\\ln \frac{r}{R_{\mathrm{o}}}\left(\frac{1}{2} \rho \omega_{\mathrm{f} 1}^{2}+\frac{3 \eta}{\phi_{r} h^{3}} \frac{\partial \bar{h}_{\mathrm{T}}}{\partial t}\right) \frac{R_{\mathrm{o}}^{2}-R_{\mathrm{i}}^{2}}{\ln R_{\mathrm{i}}-\ln R_{\mathrm{o}}}\end{gathered}$ (6)
假设摩擦材料表面微凸峰为高斯分布，平均油膜厚度的变化率可以由文献[18]得到。在流体润滑面积Av上对平均油膜压力进行积分，则可得到流体动压承载力为
$F_{\mathrm{v}}=\iint_{A_{\mathrm{v}}} \bar p \mathrm{~d} A_{\mathrm{v}}$ (7)
1.3 粗糙接触模型在离合器的实际工作过程中，铜基摩擦材料通常会发生弹塑性接触，其粗糙接触面积为：
$A_{\mathrm{c}}=\kappa {\rm{ \mathsf{ π} }}^{3}(N \beta \sigma)^{2}\left(R_{\mathrm{o}}^{2}-R_{\mathrm{i}}^{2}\right) A_{\mathrm{red}} F_{2}(H) $ (8)
$F_{2}(H)=0.5\left(H^{2}+1\right) \operatorname{erfc}(H / \sqrt{2})-H /(\sqrt{2 {\rm{ \mathsf{ π} }}}) \mathrm{e}^{-\frac{H^{2}}{2}}$ (9)
式中：κ为塑性变形系数，N和β分别为微凸峰的密度和曲率半径，σ为联合表面粗糙度均方根，Ared为非沟槽区域面积比，H=h/σ为膜厚比。
微凸体接触压力可以表示为[17]
$\begin{cases}p_{\mathrm{c}}=4.4086 \times 10^{-5} K^{\prime} E^{\prime}(4-H)^{6.804}, & H<4 \\ p_{\mathrm{c}}=0, & H \geqslant 4\end{cases}$ (10)
式中K′为接触系数，E′为当量弹性模量。
在粗糙接触面积Ac上对微凸体接触压力进行积分，则可得到微凸体粗糙接触力为
$F_{\mathrm{c}}=\iint_{A_{\mathrm{c}}} p_{\mathrm{c}} \mathrm{d} A_{\mathrm{c}}$ (11)
1.4 摩擦转矩模型湿式多片离合器的摩擦转矩Mf由黏性转矩Mv和粗糙接触转矩Mc组成。基于平均流量模型，黏性转矩表示为
$M_{\mathrm{v}}=\left(1-A_{\mathrm{red}} C\right) \int_{0}^{2 {\rm{ \mathsf{ π} }}} \int_{R_{\mathrm{i}}}^{R_{\mathrm{o}}} \eta\left(\phi_{\mathrm{f}}+\phi_{\mathrm{fs}}\right) \frac{r^{2} \Delta \omega}{h} r \mathrm{d} r \mathrm{d} \theta$ (12)
式中：?f和?fs为剪切应力系数，Δω为主被动端角速度差。
对摩擦力微元沿径向r和周向θ进行积分，得到粗糙接触转矩为
$M_{\mathrm{c}}=A_{\mathrm{red}} C \mu \int_{0}^{2 {\rm{ \mathsf{ π} }}} \int_{R_{\mathrm{i}}}^{R_{\mathrm{o}}} p_{\mathrm{c}} r^{2} \mathrm{d} r \mathrm{d} \theta$ (13)
式中μ为摩擦因数，可通过大量销盘试验数据拟合获得[19]，表示为
$\begin{aligned}\mu=&0.035+23 \mathrm{e}^{\left(\frac{-2.6 V}{(\ln T-3.2)\left((28.3 P)^{0.4}-0.87\right)}-5.16\right)}+\\& 0.08\left(\mathrm{e}^{-0.005 T}-1\right)\left(\mathrm{e}^{-0.2 V}-1\right)+\\& \frac{0.01 \ln (4 V+1)}{\mathrm{e}^{0.005 T}}-0.005 \ln (28.3 P)\end{aligned}$ (14)
式中：V为两摩擦表面线速度差，T为润滑油温度，P为摩擦副加载压力。
离合器系统的转矩平衡方程表示为
$I_{\mathrm{f} 1} \frac{\mathrm{d} \omega_{\mathrm{f} 1}}{\mathrm{~d} t}=\sum\limits_{i=1}^{Z} M_{\mathrm{f} i}-M_{\mathrm{R}}$ (15)
式中If1为被动端转动惯量，MR为被动端阻力矩。
1.5 花键阻力模型由于周向摩擦转矩的作用，当摩擦元件发生轴向移动时，花键处会产生阻碍摩擦元件轴向移动的摩擦力[20]。摩擦片受到的花键摩擦力表示为
$F_{\mathrm{f}}=\operatorname{sign}(\dot{x}) \mu_{\mathrm{f}} M_{\mathrm{f}} /\left(R_{\mathrm{f}} \cos \alpha_{\mathrm{f}}\right)$ (16)
式中：
钢片受到的花键摩擦力表示为
$F_{\mathrm{s}}=\operatorname{sign}(\dot{x}) \mu_{\mathrm{s}} M_{\mathrm{f}} /\left(R_{\mathrm{s}} \cos \alpha_{\mathrm{s}}\right)$ (17)
式中：μs为对偶钢片外花键齿摩擦因数，Rs为外花键齿节圆半径，αs为外花键齿压力角。
由于离心力的作用，润滑油流经钢片外齿花键并形成浮动支撑结构。当钢片发生轴向移动时，花键处润滑油受到剪切，产生阻尼力。钢片受到的花键阻尼力表示为
$F_{\mathrm{d}}=c_{\mathrm{s}} \dot{x}$ (18)
式中cs为阻尼系数，与外齿花键结构有关。
1.6 活塞碰撞模型分离过程中活塞回到极限位置时会与离合器毂发生碰撞，直至活塞动能被耗散为零。活塞与离合器毂的碰撞会通过活塞与第1片钢片之间的流体动压承载力影响摩擦副的分离。为了获得碰撞过程活塞的位移和速度，采用LN接触模型[21]将碰撞接触力表示为
$F_{\text {impact }}=K_{0} \xi^{n}\left[1+\frac{3\left(1-e^{2}\right)}{4} \frac{\dot\xi}{\dot\xi{}^{(-)}}\right]$ (19)
式中：K0为碰撞刚度，ξ为碰撞压缩量，n为碰撞系数，e为恢复系数，
2 数值仿真仿真开始时，湿式多片离合器处于分离状态，在控制油压的作用下依次经历接合过程、接合状态和分离过程，最终回到分离状态。使用MATLAB /Simulink软件进行仿真，仿真流程如图 3所示。首先使用初始状态或上一时间步的计算结果计算摩擦元件受力；然后通过求解受力平衡方程获得各摩擦元件加速度、速度和位移；再使用各摩擦元件位移和速度计算各间隙和各间隙变化率；最后重复该计算过程至预设仿真时长。
Fig. 3
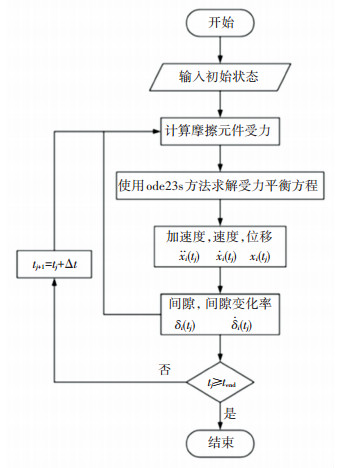图 3 湿式多片离合器工作过程仿真流程图 Fig. 3 Flow chart for working process simulation of wet multi-disc clutch 选取六摩擦副系统进行仿真研究，仿真时长为5 s。为了体现活塞与第1片钢片之间间隙δ0的变化，将其初始值设为0.05 mm，将第1摩擦副间隙δ1的初始值设为0.45 mm，而其他摩擦副间隙的初始值均为理想分离间隙0.50 mm。其他仿真输入参数如表 1所示。控制油压papp变化见图 4。
表 1
表 1 仿真输入参数 Tab. 1 Input data of simulation 参数 取值 参数 取值 Ared 0.68 MR/(N·m) 240
cs/(N·s·m-1) 0.071 4 N/m-2 7×107
dm/m 6×10-4 Ri/m 0.086
E′/GPa 4.84 Ro/m 0.124
Hfd/mm 3.2 β/m 8×10-4
Hsd/mm 2.0 η/(Pa·s) 0.026
If1/(kg·m2) 2 σ/m 8.4×10-6
m0/kg 3.00 Ψ/m2 2×10-12
m1/kg 0.45 ρ/(kg·m-3) 875
m2/kg 0.60
表 1 仿真输入参数 Tab. 1 Input data of simulation
Fig. 4
图 4 控制油压与主被动端转速变化 Fig. 4 Variation of control oil pressure and rotating speed 从0 ~第0.3 s控制油压从0 MPa线性增加至0.36 MPa；从第0.3 s~第0.5 s，控制油压从0.36 MPa快速增加至1.80 MPa，并保持1.80 MPa至第1.5 s；从第1.5 s ~第1.6 s，控制油压从1.80 MPa迅速降低至0.05 MPa，最后在第5 s衰减至0 MPa。主被动端转速变化见图 4，摩擦片转速nf2始终为1 000 r/min；钢片的初始和最终转速均为0 r/min，钢片转速nf1的变化通过仿真得到。以花键摩擦因数取值0.1为例，离合器工作过程中间隙和转矩的变化见图 5。
Fig. 5
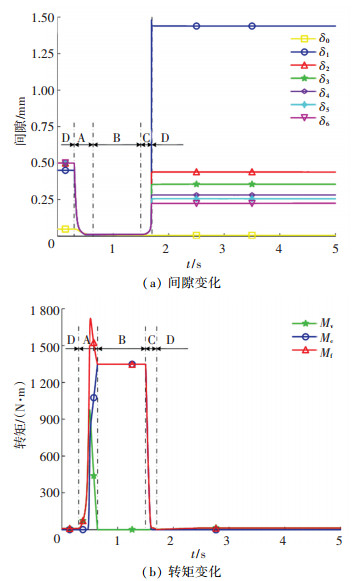图 5 离合器工作过程间隙和转矩变化 Fig. 5 Variation of gaps and torque in a working cycle 根据转速、油压和间隙的变化，对湿式离合器的工作过程进行划分：控制油压作用力在第0.300 s之后大于回位弹簧力，各间隙开始减小，接合过程(A)开始；钢片和摩擦片的转速差在第0.638 s降为零，主被动端完成同步，离合器进入接合状态(B)；控制油压在第1.500 s开始下降，分离过程(C)开始；各摩擦副间隙在第1.698 s之后稳定，分离过程结束，离合器进入分离状态(D)。
3 花键摩擦因数对分离过程影响为了研究花键摩擦因数对湿式多片离合器分离过程的影响，结合润滑条件下钢对钢摩擦因数的实际取值，设置花键摩擦因数分别为0、0.06、0.08、0.10和0.12进行仿真，并将其依次编号为U1、U2、U3、U4和U5。不同花键摩擦因数下分离过程结束后的各摩擦副间隙如表 2所示。
表 2
表 2 不同花键摩擦因数下仿真结果 Tab. 2 Simulation results with different spline friction coefficients 序号 花键摩擦因数 δ1/mm δ2/mm δ3/mm δ4/mm δ5/mm δ6/mm 不均匀系数 分离时刻/s U1 0 0.499 3 0.499 3 0.499 3 0.499 3 0.499 3 0.499 3 0.500 3 1.696
U2 0.06 1.292 9 0.477 0 0.387 9 0.309 9 0.281 3 0.246 9 0.546 8 1.698
U3 0.08 1.395 3 0.450 8 0.365 4 0.290 2 0.263 2 0.231 0 0.556 6 1.698
U4 0.10 1.439 1 0.439 2 0.355 2 0.282 0 0.256 2 0.224 3 0.561 0 1.698
U5 0.12 1.449 3 0.435 7 0.352 4 0.280 3 0.254 9 0.223 4 0.562 0 1.698
表 2 不同花键摩擦因数下仿真结果 Tab. 2 Simulation results with different spline friction coefficients
3.1 分离过程持续时间不同花键摩擦因数下分离过程中各间隙的变化见图 6。在分离过程中，各摩擦副间隙首先缓慢增大，再迅速增大，然后剧烈波动，最后趋于稳定。当各摩擦副间隙均稳定后，分离过程结束。如图 6(a)，花键摩擦因数为零时，各副间隙在第1.696 s稳定，分离过程的持续时间为0.196 s。如图 6(b)~6(e)，当花键摩擦因数不为零时，各副间隙均在第1.698 s稳定，分离过程的持续时间均为0.198 s。因此，花键摩擦因数大小对分离过程持续时间几乎没有影响。
Fig. 6
图 6 不同花键摩擦因数下分离过程间隙变化 Fig. 6 Variation of gaps in the disengaging process with different spline friction coefficients 3.2 分离间隙均匀度如图 6所示，各摩擦副间隙在经过波动之后稳定，由于花键摩擦力和阻尼力的衰减作用，其波动程度从第1摩擦副间隙δ1至第6摩擦副间隙δ6依次减弱。然而活塞与第1片钢片之间的间隙δ0始终保持一个很小的值，这说明在分离过程中第1片钢片紧随活塞的运动而运动。如表 2所示，当不考虑花键摩擦时，分离过程结束后各摩擦副间隙相等；而考虑花键摩擦后，各组摩擦副间隙均从第1副至第6副依次减小。
可以发现，通过直接比较各摩擦副间隙的大小并不能直观地判断不同花键摩擦因数下分离间隙的均匀程度。因此提出不均匀系数Π表征摩擦副分离的均匀程度，不均匀系数表示为
$\varPi=\frac{1}{Z} \sum\limits_{i=1}^{Z} \frac{1}{1+\delta_{i} / \delta^{*}}$ (20)
式中δ*为理想均匀分离间隙。不均匀系数与摩擦副间隙大小成反比，与分离间隙均匀度成反比，并且1.0＞Π＞0.5。
如图 7所示，不均匀系数随着摩擦副间隙的增大首先缓慢减小然后迅速减小，并随间隙的波动出现波动，当摩擦副间隙稳定后，不均匀系数也随之稳定。不同花键摩擦因数下，分离过程结束后的不均匀系数计算结果如表 2所示。当不考虑花键摩擦时，各摩擦副实现了均匀分离，由于活塞与第1片钢片之间间隙δ0的存在，各摩擦副间隙为0.499 3 mm而不是0.500 0 mm，因此不均匀系数为0.500 3而不是0.500 0。随着花键摩擦因数从0.06线性增加至0.12，不均匀系数从0.546 8增加至0.562 0。因此，花键摩擦显著恶化了湿式多片离合器分离间隙的均匀程度，但是其影响随摩擦因数的增加逐渐减弱。
Fig. 7
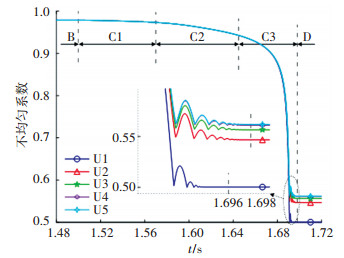图 7 不同花键摩擦因数下分离过程不均匀系数变化 Fig. 7 Variation of non-uniformity coefficient in the disengaging process with different spline friction coefficients 3.3 分离过程摩擦转矩不同花键摩擦因数下分离过程转矩变化如图 8所示。图 8(b)中，不同花键摩擦因数下的黏性转矩均在第1.569 s和第1.570 s之间开始增加，摩擦副从边界润滑阶段(C1)进入混合润滑阶段(C2)，并且U1最先发生润滑状态的转变，然后依次是U5至U2；如图 8(a)所示，不同花键摩擦因数下的粗糙接触转矩均在第1.644 s和第1.645 s之间开始小于10-6 N·m，摩擦副进入流体动压润滑阶段(C3)，同样U1最先发生润滑状态的转变，但接下来依次是U2至U5。
Fig. 8
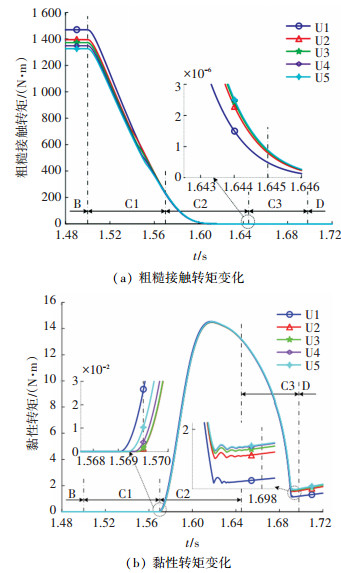图 8 不同花键摩擦因数下分离过程转矩变化 Fig. 8 Variation of torque in the disengaging process with different spline friction coefficients 如图 8(a)所示，在边界润滑和混合润滑阶段，粗糙接触转矩首先迅速减小，然后缓慢减小至零。在分离过程的开始，粗糙接触转矩随着花键摩擦因数的增加而依次减小，这是由于花键摩擦对控制油压的衰减作用导致的。而在混合润滑阶段的最后时刻，粗糙接触转矩随着花键摩擦因数的增加而依次增加。因此在分离过程中，花键摩擦因数越小，粗糙接触转矩的衰减速率越大。
如图 8(b)所示，在混合润滑和流体动压润滑阶段，黏性转矩首先迅速增大到约14.5 N·m后又快速减小，并随着间隙的波动出现波动，当间隙稳定后，随着转速差的增大而缓慢增大。由图 6和图 8(b)可知，随着各摩擦副间隙的缓慢增大，不同花键摩擦因数下的黏性转矩几乎没有差异；而当各摩擦副间隙迅速增大时，花键摩擦对分离均匀度的恶化作用开始显现，在分离过程末期，黏性转矩随着花键摩擦因数的增大而增大，但是增大的幅度逐渐减小。
4 结论1) 湿式多片离合器分离过程中，各摩擦副间隙首先缓慢增大，再迅速增大，然后剧烈波动，稳定之后分离过程结束，并且第1片钢片紧随活塞的运动而运动。
2) 花键摩擦因数对分离过程持续时间几乎没有影响。花键摩擦因数为零时，各摩擦副均匀分离，不均匀系数为0.500 3；考虑花键摩擦后，各摩擦副间隙从第1副至第6副依次减小，并且随着花键摩擦因数的增加，不均匀系数从0.546 8增加至0.562 0。花键摩擦因数的增加显著恶化了分离间隙均匀度。
3) 湿式多片离合器分离过程中，粗糙接触转矩首先迅速减小，然后缓慢减小至零，并且花键摩擦因数越小，粗糙接触转矩的初始值越大，衰减速率也越大；黏性转矩首先迅速增大，然后快速减小，经过波动之后缓慢增大，并且花键摩擦因数越大，分离过程末期的黏性转矩越大。
参考文献
[1] 马彪, 李国强, 李和言, 等. 基于改进平均流量模型的离合器接合特性仿真[J]. 吉林大学学报(工学版), 2014, 44(6): 1157.
MA Biao, LI Guoqiang, LI Heyan, et al. Simulation of wet clutch engagement characteristics based on advanced average flow model[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1557. DOI:10.13229/j.cnki.jdxbgxb201406004
[2] YU Liang, MA Biao, CHEN Man, et al. Numerical and experimental studies on the characteristics of friction torque based on wet paper-based clutches[J]. Tribology International, 2019, 131: 541. DOI:10.1016/j.triboint.2018.09.019
[3] YU Liang, MA Biao, CHEN Man, et al. Variation mechanism of the friction torque in a Cu-based wet clutch affected by operating parameters[J]. Tribology International, 2020, 147: 106169. DOI:10.1016/j.triboint.2020.106169
[4] JANG J Y, KHONSARI M M. Thermal characteristics of a wet clutch[J]. Journal of Tribology, 1999, 121(3): 610. DOI:10.1115/1.2834111
[5] JANG J Y, KHONSARI M M, MAKI R. Three-dimensional thermohydrodynamic analysis of a wet clutch with consideration of grooved friction surfaces[J]. Journal of Tribology, 2011, 133(1): 011703. DOI:10.1115/1.4003019
[6] LI M, KHONSARI M M, MCCARTHY D M C, et al. Parametric analysis for a paper-based wet clutch with groove consideration[J]. Tribology International, 2014, 80: 222. DOI:10.1016/j.triboint.2014.06.023
[7] 吴健鹏, 马彪, 李和言, 等. 加速寿命过程的湿式摩擦副滑摩温升特性[J]. 哈尔滨工业大学学报, 2019, 51(7): 103.
WU Jianpeng, MA Biao, LI Heyan, et al. Temperature rise of wet friction pair during sliding in the accelerated life test[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 103. DOI:10.11918/j.issn.0367-6234.201804195
[8] 何松. 离合器摩擦界面比压扰动影响研究[D]. 北京: 北京理工大学, 2015
HE Song. Study on the influence of pressure disturbance on the friction pair interface of clutch[D]. Beijing: Beijing Institute of Technology, 2015
[9] 于亮, 李和言, 马彪, 等. 多片离合器轴向平均比压的衰减特性[J]. 吉林大学学报(工学版), 2018, 48(4): 990.
YU Liang, LI Heyan, MA Biao, et al. Analysis and verification for average axial pressure attenuation of multi-disc clutch[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(4): 990. DOI:10.13229/j.cnki.jdxbgxb20170269
[10] 张恒, 李和言, 昌和, 等. 湿式多片离合器摩擦转矩衰减特性分析[J]. 哈尔滨工业大学学报, 2018, 50(7): 94.
ZHANG Heng, LI Heyan, CHANG He, et al. Experimental study on attenuation characteristics of friction torque transferred by the wet multi-disc clutch[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 94. DOI:10.11918/j.issn.0367-6234.201709141
[11] IQBAL S, AL-BENDER F, PLUYMERS B, et al. Model for predicting drag torque in open multi-disks wet clutches[J]. Journal of Fluids Engineering, 2014, 136(2): 021103. DOI:10.1115/1.4025650
[12] HU Jibin, HOU Shiyang, WEI Chao. Drag torque modeling at high circumferential speed in open wet clutches considering plate wobble and mechanical contact[J]. Tribology International, 2018, 124: 102. DOI:10.1016/j.triboint.2018.03.029
[13] WU Wei, XIAO Bingqing, HU Jibin, et al. Experimental investigation on the air-liquid two-phase flow inside a grooved rotating-disk system: flow pattern maps[J]. Applied Thermal Engineering, 2018, 133: 33. DOI:10.1016/j.applthermaleng.2018.01.031
[14] 师路骐, 马彪, 李和言, 等. 全程转速下浮动支撑湿式离合器带排转矩计算模型与验证[J]. 兵工学报, 2018, 39(9): 1665.
SHI Luqi, MA Biao, LI Heyan, et al. Modeling and experimental validation of drag torque of wet multi-disk clutch with spline connected restriction in full speed range[J]. Acta Armamentarii, 2018, 39(9): 1665. DOI:10.3969/j.issn.1000-1093.2018.09.001
[15] WANG Pengchuan, KATOPODES N, FUJII Y. Statistical modeling of plate clearance distribution for wet clutch drag analysis[J]. SAE International Journal of Passenger Cars Mechanical Systems, 2018, 11(1): 76. DOI:10.4271/06-11-01-0007
[16] PATIR N, CHENG H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Lubrication Technology, 1978, 100(1): 12. DOI:10.1115/1.3453103
[17] PATIR N, CHENG H S. Application of average flow model to lubrication between rough sliding surfaces[J]. Journal of Lubrication Technology, 1979, 101(2): 220. DOI:10.1115/1.3453329
[18] BERGER E J, SADEGHI F, KROUSGRILL C M. Analytical and numerical modeling of engagement of rough, permeable, grooved wet clutches[J]. Journal of Tribology, 1997, 119(1): 143. DOI:10.1115/1.2832450
[19] ZHAO Erhui, MA Biao, LI Heyan. Numerical and experimental studies on tribological behaviors of Cu-based friction pairs from hydrodynamic to boundary lubrication[J]. Tribology Transactions, 2017, 61(2): 347. DOI:10.1080/10402004.2017.1323145
[20] YU Liang, MA Biao, CHEN Man, et al. Thermodynamic differences of different friction pairs in a multidisc clutch caused by spline friction: numerical simulation and experimental verification[J]. Tribology Transactions, 2019, 62(4): 724. DOI:10.1080/10402004.2019.1610533
[21] LANKARANI H M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369. DOI:10.1115/1.2912617
