无线携能通信时隙与功率联合优化算法研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编哈尔滨工业大学/2020-12-05

无线携能通信时隙与功率联合优化算法研究

宋志群^1,2,刘玉涛²,吕玉静²,张中兆¹

(1.哈尔滨工业大学电子与信息工程学院,哈尔滨 150001; 2.中国电子科技集团公司第五十四研究所,石家庄 050000)

摘要:

传统通信系统由于不能够有效利用射频信号的能量会导致传输能耗较高,所以必须合理分配资源,在信息和能量传输间获得折中,即保证充足的传输能量并尽可能提高系统的信息传输性能.因此,为了节约通信系统的能量,本文提出通信系统在多个时隙同时传输信息和能量从而实现无线携能通信.首先,将传输时间分成若干时隙,发射机按照要求在不同时隙内发送信息或者能量；然后,接收机在对应时隙内接收信息或者收集能量,并利用收集的能量提供电路耗能；最后,通过联合优化时隙和功率分配,在保证系统能量需求基础上最大化系统传输速率.仿真结果表明:相比等时间功率分配算法,提出算法的传输效率提高了约40 bps；且随着时隙数增加,提出算法性能显著提高.当传输能量增加时,可分配的信息功率更大；而当能量需求增加时,信息功率会降低,更多的功率用于能量传输.因此,提出算法通过为信息传输和能量采集合理分配时隙和功率,保证充足的采集能量基础上,最大化信息传输性能,系统通过采集无线能量有效提高了传输性能.

关键词: 多时隙无线携能通信吞吐率拉格朗日优化

DOI：10.11918/201902073

分类号:TN925

文献标识码:A

基金项目:国家自然科学基金(2,3)

Research on joint optimization algorithm for time slot and power in SWIPT

SONG Zhiqun^1,2,LIU Yutao²,Lü Yujing²,ZHANG Zhongzhao¹

(1.School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China; 2.The 54th Research Institute of China Electronic Technology Group Corporation, Shijiazhuang 050000, China)

Abstract:

Traditional communication system fails to utilize the energy of radio frequency signals effectively, which can result in high transmission energy consumption. Therefore, resources must be allocated reasonably to achieve a compromise between information and energy transmission. That is to ensure sufficient transmission energy and improve the information transmission performance of the system as much as possible. In order to save the energy of the communication system, this paper proposes that the communication system simultaneously transmits information and energy in multiple time slots to realize Simultaneous Wireless Information and Power Transfer (SWIPT). First, the transmission time was divided into a number of time slots, and the transmitter transmitted information or energy in different time slots as required. Then, the receiver collected information or harvested energy in the corresponding time slot, and the obtained energy was used to provide circuit energy consumption. Finally, by jointly optimizing the time slot and power allocation, the system transmission rate was maximized based on the guaranteed system energy requirements. Simulation results show that compared with the equal-time power allocation algorithm, the transmission efficiency of the proposed algorithm was improved by about 40 bps, and the performance was significantly improved with the increase of the number of the time slots. When the transmission energy increased, the distributable information power was greater. When the energy demand increased, the information power decreased, and more power was used for energy transmission. Hence, an algorithm was proposed to maximize the performance of information transmission by reasonably allocating time slots and power for information transmission and energy harvesting to ensure sufficient acquisition energy. Therefore, the proposed algorithm could improve the transmission performance effectively via harvesting the wireless power.

Key words: multi-slot Simultaneous Wireless Information and Power Transfer throughput Lagrangian optimization

宋志群, 刘玉涛, 吕玉静, 张中兆. 无线携能通信时隙与功率联合优化算法研究[J]. 哈尔滨工业大学学报, 2020, 52(5): 35-40. DOI: 10.11918/201902073. 复制到剪切板

SONG Zhiqun, LIU Yutao, Lü Yujing, ZHANG Zhongzhao. Research on joint optimization algorithm for time slot and power in SWIPT[J]. Journal of Harbin Institute of Technology, 2020, 52(5): 35-40. DOI: 10.11918/201902073. 复制到剪切板

基金项目国家自然科学基金(61571162, 61871153) 作者简介宋志群(1963-), 男, 高级工程师(研究员级), 博士研究生通信作者宋志群, zhiqunsy@163.com 文章历史收稿日期: 2019-02-23

Abstract            Full text            Figures/Tables            PDF

无线携能通信时隙与功率联合优化算法研究
宋志群^1,2, 刘玉涛², 吕玉静², 张中兆¹
1. 哈尔滨工业大学电子与信息工程学院, 哈尔滨 150001;
2. 中国电子科技集团公司第五十四研究所, 石家庄 050000

收稿日期: 2019-02-23
基金项目: 国家自然科学基金(61571162, 61871153)
作者简介: 宋志群(1963-), 男, 高级工程师(研究员级), 博士研究生
通信作者: 宋志群, zhiqunsy@163.com

摘要: 传统通信系统由于不能够有效利用射频信号的能量会导致传输能耗较高，所以必须合理分配资源，在信息和能量传输间获得折中，即保证充足的传输能量并尽可能提高系统的信息传输性能.因此，为了节约通信系统的能量，本文提出通信系统在多个时隙同时传输信息和能量从而实现无线携能通信.首先，将传输时间分成若干时隙，发射机按照要求在不同时隙内发送信息或者能量；然后，接收机在对应时隙内接收信息或者收集能量，并利用收集的能量提供电路耗能；最后，通过联合优化时隙和功率分配，在保证系统能量需求基础上最大化系统传输速率.仿真结果表明：相比等时间功率分配算法，提出算法的传输效率提高了约40 bps；且随着时隙数增加，提出算法性能显著提高.当传输能量增加时，可分配的信息功率更大；而当能量需求增加时，信息功率会降低，更多的功率用于能量传输.因此，提出算法通过为信息传输和能量采集合理分配时隙和功率，保证充足的采集能量基础上，最大化信息传输性能，系统通过采集无线能量有效提高了传输性能.
关键词: 多时隙    无线携能通信    吞吐率    拉格朗日优化
Research on joint optimization algorithm for time slot and power in SWIPT
SONG Zhiqun^1,2, LIU Yutao², Lü Yujing², ZHANG Zhongzhao¹
1. School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China;
2. The 54th Research Institute of China Electronic Technology Group Corporation, Shijiazhuang 050000, China

Abstract: Traditional communication system fails to utilize the energy of radio frequency signals effectively, which can result in high transmission energy consumption. Therefore, resources must be allocated reasonably to achieve a compromise between information and energy transmission. That is to ensure sufficient transmission energy and improve the information transmission performance of the system as much as possible. In order to save the energy of the communication system, this paper proposes that the communication system simultaneously transmits information and energy in multiple time slots to realize Simultaneous Wireless Information and Power Transfer (SWIPT). First, the transmission time was divided into a number of time slots, and the transmitter transmitted information or energy in different time slots as required. Then, the receiver collected information or harvested energy in the corresponding time slot, and the obtained energy was used to provide circuit energy consumption. Finally, by jointly optimizing the time slot and power allocation, the system transmission rate was maximized based on the guaranteed system energy requirements. Simulation results show that compared with the equal-time power allocation algorithm, the transmission efficiency of the proposed algorithm was improved by about 40 bps, and the performance was significantly improved with the increase of the number of the time slots. When the transmission energy increased, the distributable information power was greater. When the energy demand increased, the information power decreased, and more power was used for energy transmission. Hence, an algorithm was proposed to maximize the performance of information transmission by reasonably allocating time slots and power for information transmission and energy harvesting to ensure sufficient acquisition energy. Therefore, the proposed algorithm could improve the transmission performance effectively via harvesting the wireless power.
Keywords: multi-slot    Simultaneous Wireless Information and Power Transfer    throughput    Lagrangian optimization
随着无线通信的迅速发展，无线设备对能量的需求显著增加，导致通信能耗需求变大.因此，如何降低通信系统能耗实现绿色通信成为当前研究热点^[1-2].自然环境中的无线能量非常丰富，包括手机无线能量、广播无线能量、卫星无线能量等，这些无线能量可以被通信系统免费获取和利用.此外，无线能量不同于太阳能和风能，能量采集设备可以在传输源的范围内自由移动，不受时间和场地限制，几乎可工作在任何环境下^[3-5].文献[6-7]指出无线能量传输容易实现，能量收集电路的核心是由二极管和电容组成的整流电路，成本比布设电源线或更换电池所需的日常维护成本要低.因此，无线能量传输已经成为绿色通信的首选技术之一^[8].

无线信号既包含信息也携带能量，无线携能通信(Simultaneous Wireless Information and Power Transfer，SWIPT)在接收信息的同时采集射频能量.目前，无线携能通信主要通过时隙分配和功率分流两种模型实现.时隙分配模型中，为信息传输和能量传输分配不同的时隙，接收机在对应的时隙解码信息和采集能量；功率分流模型中，为信息传输和能量传输分配不同的功率流，接收机利用对应的功率流解码信息和采集能量^[9-12].文献[13]通过优化时隙和功率流的分配系数，能够在保证采集能量充足的基础上，最大化信息传输性能，降低了能量传输对资源的消耗.为了削弱信道衰落对无线携能通信的影响，文献[14]提出能量传输的优化算法，能够在信息传输和能量传输间获得权衡，进而提高无线携能通信的性能.文献[15-19]提出了多天线传输下的无线携能通信，采用部分天线用作能量传输，其余天线用于信息传输，提高了无线携能通信的分级增益.文献[20-21]提出了MIMO系统下的无线携能通信，仿真表明MIMO系统通过大量的天线发射能够充分提高传输容量和能量采集量.文献[22-24]提出了多载波和多用户场景下的无线携能通信，通过为信息传输和能量传输合理分配载波和用户资源，有效优化了无线携能通信的性能.

传统方案中，信息和能量均采用相等时间传输，没有考虑到信道时变对性能的影响.本文研究了多时隙无线携能通信系统，发射机可以在任意时隙传输信息或者能量，通过时隙和功率的联合优化分配，有效提高系统在衰落信道下的传输效率.

1 系统模型本文提出一种多时隙无线携能通信系统模型，其模型如图 1所示.

Fig. 1
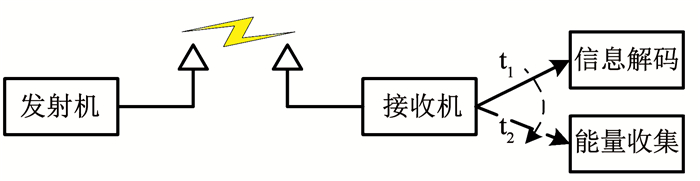点击查看原图

图 1 无线携能通信系统模型 Fig. 1 Multi-slot SWIPT model

发射机发送的无线信号由于信息调制而携带信息，且通过电磁波传输而含有射频能量.接收机除了具有传统的信息解码单元还具有能量收集单元，接收机在特定时隙解码信息或采集能量，采集的能量可以为通信系统提供电路耗能.能量收集单元主要由整流电路构成，用于将交流信号转化成直流电能.

如图 2所示，多时隙无线携能通信系统将传输时间分成若干个时隙，发射机在每个时隙内按照要求发送信息信号或者能量信号，接收机在对应时隙内解码信息或者收集能量.假设总时隙数为N，每个时隙长度为τ.考虑时变信道，发射机在第i个时隙的发射功率为p_i.发射机可以选择任何时隙发送信息或者能量，假设信息时隙集合为Ω_I，能量时隙集合为Ω_E，Ω_I和Ω_E满足

Fig. 2
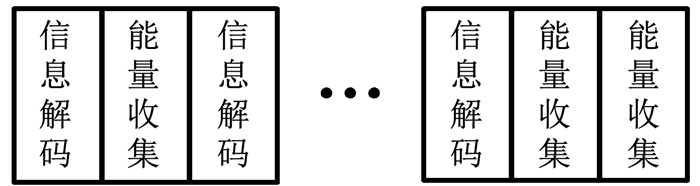点击查看原图

图 2 多时隙无线携能通信时隙分配示意 Fig. 2 Time slot allocation for multi-slot SWIPT

${{{\bf \Omega }}_1} \cap {{{\bf \Omega }}_{\rm{E}}} = \emptyset , {{{\bf \Omega }}_1} \cup {{{\bf \Omega }}_{\rm{E}}} = {{{\bf \Omega }}_{\rm{N}}}.$ (1)

式中Ω_N为所有时隙集合.

香农定理定义通信系统信道容量为

$R = \log \left( {1 + \frac{S}{N}} \right).$ (2)

式中：S是传输信号功率，N是噪声功率.因此，通信系统在信息时隙内传输信息，归一化总吞吐量(设信道带宽为1 Hz)表示为

$R = \sum\limits_{i \in {{{\bf \Omega }}_1}} {\log } \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right).$ (3)

式中：h_i是i时隙的信道增益，σ_i²是信道噪声.能量时隙内，通信系统总采集能量表示为

${E_H} = \eta \sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {\left( {{p_i}h_i^2 + \sigma _i^2} \right)} .$ (4)

式中：η为能量采集效率.发射机的总发射能量为

${E_{\rm{T}}} = \tau \sum\limits_{i = 1}^N {{p_i}} .$ (5)

发射机的发射功率越大，发射信号携带的射频能量越高，接收端能够采集的能量也越大.然而，当总发射能量一定时，信号携带的能量是恒定的，因此采集的能量越大，用于信息传输的能量反而越少.因此，需要对模型优化，通过为信息传输和能量采集合理分配时隙和功率，保证充足的采集能量基础上，最大化信息传输性能.

2 模型优化及求解本文通过联合优化时隙分配集合和时隙功率，最大化通信系统的传输效率，同时保证如下约束条件：系统的采集能量高于最小能量需求E_min；系统总发射能量小于最大发射能量E_max.优化问题表示为

$\begin{array}{*{20}{c}}{\mathop {\max }\limits_{{{{\bf \Omega }}_{\rm{I}}}, {{{\bf \Omega }}_{\rm{E}}}, \left\{ {{p_i}} \right\}} R = \sum\limits_{i \in {{{\bf \Omega }}_{\rm{I}}}} {\log } \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right), }\\{{\rm{s}}.\;{\rm{t}}.\;\;\;\;{E_{\rm{H}}} \ge {E_{{\rm{min}}}}, }\\{{E_{\rm{T}}} \le {E_{{\rm{max}}}}, }\\{{p_i} \ge 0, i = 1, 2, \cdots , N, }\\{{{{\bf \Omega }}_{\rm{I}}} \cap {{{\bf \Omega }}_{\rm{E}}} = \emptyset , {{{\bf \Omega }}_{\rm{I}}} \cup {{{\bf \Omega }}_{\rm{E}}} = {{{\bf \Omega }}_{\rm{N}}}.}\end{array}$ (6)

利用拉格朗日乘子法求解优化问题，拉格朗日函数表示为

$F\left( {{\mu _1}, {\mu _2}} \right) = \mathop {\max }\limits_{{{{\bf \Omega }}_{\rm{I}}}, {{{\bf \Omega }}_{\rm{E}}}, \left\{ {{p_i}} \right\}} L\left( {{{{\bf \Omega }}_{\rm{I}}}, {{{\bf \Omega }}_{\rm{E}}}, \left\{ {{p_i}} \right\}} \right).$ (7)

式中：μ₁≥0和μ₂≥0是拉格朗日乘子；函数L(Ω_I, Ω_E, {p_i})表示为

$\begin{array}{*{20}{c}}{L\left( {{{{\bf \Omega }}_{\rm{I}}}, {{{\bf \Omega }}_{\rm{E}}}, \left\{ {{p_i}} \right\}} \right) = \sum\limits_{i \in {{{\bf \Omega }}_{\rm{I}}}} {\log } \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right) + }\\{{\mu _1}\left( {\eta \sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {\left( {{p_i}h_i^2 + \sigma _i^2} \right)} - {E_{\min }}} \right) + }\\{{\mu _2}\left( {{E_{\max }} - \tau \sum\limits_{i = 1}^N {{p_i}} } \right).}\end{array}$ (8)

函数L(Ω_I, Ω_E, {p_i})是一系列凸函数和线性函数的线性叠加，因此也是凸函数.根据对偶原理，函数L是凸函数，表明优化问题具有对偶性.因此，简化后的优化问题表示为

$\begin{array}{*{20}{c}}{\mathop {\min }\limits_{{\mu _1}, {\mu _2}} F\left( {{\mu _1}, {\mu _2}} \right), }\\{{\rm{s}}.\;{\rm{t}}.\;\;{\mu _1} \ge 0;{\mu _2} \ge 0.}\end{array}$ (9)

μ₁和μ₂的最优解可以用次梯度方法求解，表示为：

$\begin{array}{*{20}{c}}{\mu _1^{(t + 1)} = \mu _1^{(t)} + \kappa _1^{(t)}\left( {\sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {\left( {{p_i}h_i^2 + \sigma _i^2} \right)} - {E_{\min }}} \right), }\\{\mu _2^{(t + 1)} = \mu _2^{(t)} + \kappa _2^{(t)}\left( {{E_{\max }} - \tau \sum\limits_{i = 1}^N {{p_i}} } \right).}\end{array}$ (10)

式中：t是迭代序号，κ₁^(t)和κ₂^(t)是迭代步长，符号(x)⁺表示x和0之间的最大值.当式(9)收敛时得到最优的μ₁和μ₂，此时满足约束条件E_H=E_min和E_T=E_max.因为优化问题包含Ω_E、Ω_I和{p_i}3个参数，我们将优化问题(5)分解为功率优化、时隙优化和联合优化3个子优化问题.

2.1 功率优化固定时隙集合Ω_E和Ω_I，优化功率{p_i}，此时Ω_E和Ω_I看做两个常数集合.{p_i}的最优值通过如下公式获得

$\frac{{\partial L\left( {\left\{ {{p_i}} \right\}} \right)}}{{\partial {p_i}}} = 0, i = 1, 2, \cdots , N.$ (11)

将式(8)带入式(11)，通过求导数得到

$\frac{{h_i^2}}{{\sigma _i^2 + {p_i}h_i^2}} - {\mu _2}\tau = 0.$ (12)

当i∈Ω_I时，考虑到p_i≥0，可以得到

${p_i} = {\left( {\frac{1}{{{\mu _2}\tau }} - \frac{{\sigma _i^2}}{{h_i^2}}} \right)^ + }, $ (13)

当i∈Ω_E时，可以得到

${p_i} = \left\{ {\begin{array}{*{20}{l}}{{p_{\max }}, }&{\frac{{{\mu _1}}}{{{\mu _2}}} \ge \frac{\tau }{{\eta h_i^2}};}\\{0, }&{\frac{{{\mu _1}}}{{{\mu _2}}} < \frac{\tau }{{\eta h_i^2}}.}\end{array}} \right.$ (14)

式中：p_max为子时隙功率最大值.将式(14)得到的{p_i}代入式(10)以更新μ₁和μ₂，将新的μ₁和μ₂代入式(14)重新求得{p_i}，然后重新更新μ₁和μ₂，如此反复迭代直至μ₁和μ₂均收敛.

2.2 时隙优化当给定{p_i}时，可以进一步优化Ω_E和Ω_I.根据式(8)可以得到：

$\begin{array}{*{20}{c}}{L\left( {{{{\bf \Omega }}_{\rm{I}}}, {{{\bf \Omega }}_{\rm{E}}}} \right) = \sum\limits_{i \in {{{\bf \Omega }}_{\rm{I}}}} {\log } \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right) + }\\{{\mu _1}\left( {\eta \sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {\left( {{p_i}h_i^2 + \sigma _i^2} \right)} - {E_{\min }}} \right) + }\\{{\mu _2}\left( {{E_{\max }} - \tau \sum\limits_{i = 1}^N {{p_i}} } \right) = }\\{\sum\limits_{i \in {{{\bf \Omega }}_E}} {\left( {{\mu _1}\eta \left( {{p_i}h_i^2 + \sigma _i^2} \right) - \log \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right)} \right)} + }\\{\sum\limits_{i \in {{{\bf \Omega }}_{\rm{N}}}} {\left( {\log \left( {1 + \frac{{{p_i}h_i^2}}{{\sigma _i^2}}} \right) - {\mu _2}\tau {p_i}} \right)} + {\mu _2}{E_{\max }} - {\mu _1}{E_{\min }} = }\\{\sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {{\mathit{\Phi }_i}} + \Psi .}\end{array}$ (15)

其中：$ \varPhi_{i}=\mu_{1} \eta\left(p_{i} h_{i}^{2}+\sigma_{i}^{2}\right)-\log \left(1+\frac{p_{i} h_{i}^{2}}{\sigma_{i}^{2}}\right)$和Ψ=$ \sum\limits_{i \in \mathbf{\Omega}_{{\rm N}}}\left(\log \left(1+\frac{p_{i} h_{i}^{2}}{\sigma_{i}^{2}}\right)-\mu_{2} \tau p_{i}\right)+\mu_{2} E_{\max }-\mu_{1} E_{\min }$.显然当{p_i}固定时，Ψ为一恒定值，因此优化问题只需$ \sum\limits_{i \in \mathbf{\Omega}_{\mathrm{E}}} \varPhi_{i}$取得最大值，即

${{\bf \Omega }}_{\rm{E}}^* = \mathop { {\rm argmax} }\limits_{{{{\bf \Omega }}_{\rm{E}}}} \sum\limits_{i \in {{{\bf \Omega }}_{\rm{E}}}} {{\Phi _i}} .$ (16)

进一步可以得出Φ_i>0, ?i∈Ω_E，即只需选择所有Φ_i>0的子载波归为Ω_E，然后Ω_I=Ω_N－Ω_E.

2.3 联合优化联合优化采用交替迭代优化算法，即：初始化Ω_E和Ω_I，优化{p_i}；固定优化后的{p_i}，优化Ω_E和Ω_I；然后固定优化后的Ω_E和Ω_I，继续优化{p_i}；如此往复直至收敛.

算法流程描述如下：

1) 定义时隙集合为Ω_N={1, 2, 3, …, N}，初始化$\mathbf{\Omega}_{E}=\left\{1, 2, \cdots, \frac{N}{2}\right\} $和${\bf\Omega}_{{\rm I}}=\left\{\frac{N+1}{2}, \cdots, N-1, N\right\} $；

2) 利用初始时隙集合，根据公式(14)优化功率{p_i}；

3) 利用{p_i}计算Φ_i值；

4) 利用式(16)重新计算Ω_E和Ω_I；

5) 反复执行步骤(2)和(4)直至集合Ω_E和Ω_I不再改变.

因为目标函数R是凸函数，因此每次迭代过程R值都是非减的，即：

$\begin{array}{*{20}{c}}{R\left( {{{\bf \Omega }}{{(t)}_{\rm{I}}}, {{\bf \Omega }}{{(t)}_{\rm{E}}}, \left\{ {p_i^{(t)}} \right\}} \right) \le }\\{R\left( {{{\bf \Omega }}{{(t + 1)}_{\rm{I}}}, {{\bf \Omega }}{{(t)}_{\rm{E}}}, \left\{ {p_i^{(t)}} \right\}} \right) \le }\\{R\left( {{{\bf \Omega }}{{(t + 1)}_{\rm{I}}}, {{\bf \Omega }}{{(t + 1)}_{\rm{E}}}, \left\{ {p_i^{(t)}} \right\}} \right) \le }\\{R\left( {{{\bf \Omega }}{{(t + 1)}_{\rm{I}}}, {{\bf \Omega }}{{(t + 1)}_{\rm{E}}}, \left\{ {p_i^{(t + 1)}} \right\}} \right).}\end{array}$ (17)

因此当R值收敛时，Ω_I、Ω_E和{p_i^(t)}均收敛.

3 仿真分析仿真中时隙数最大设置为20，噪声功率为1 mW，能量采集效率为0.8，时隙长为1 s，信道服从瑞利分布.仿真分析了提出算法和传统的等时间功率分配算法的性能.等时间功率分配算法是指信息和能量分配相同数量的传输时隙，并且各自时隙分配相同的功率.

图 3给出了不同算法下吞吐率随最大发射能量的变化，结果表明提出算法相比等时间功率分配算法具有明显的性能优势，当E_max=80 mJ时，提出算法的吞吐率提高了约40 bps；此外当发射能量提高时，提出算法的吞吐率提高，表明提出算法能够择优分配功率.

Fig. 3
点击查看原图

图 3 不同算法下吞吐量随最大发射能量的变化 Fig. 3 Throughput variation with maximum emission energy under different algorithms

图 4表示不同时隙数下吞吐量随发射能量的变化.可以看出当时隙数增加，吞吐量也会有所提高.表明增加时隙数可以为无线携能通信分配更多的可用时隙.

Fig. 4
点击查看原图

图 4 不同时隙数下吞吐量随发射能量的变化 Fig. 4 Throughput variation with transmit energy in different time slots

图 5表示吞吐率随最小能量需求的变化，可以看出能量需求越高，吞吐率越低，表明能量采集会占用一定的传输资源.因此，必须合理分配资源，在信息和能量传输间获得折中，即保证充足的传输能量并尽可能提高信息传输性能.

Fig. 5
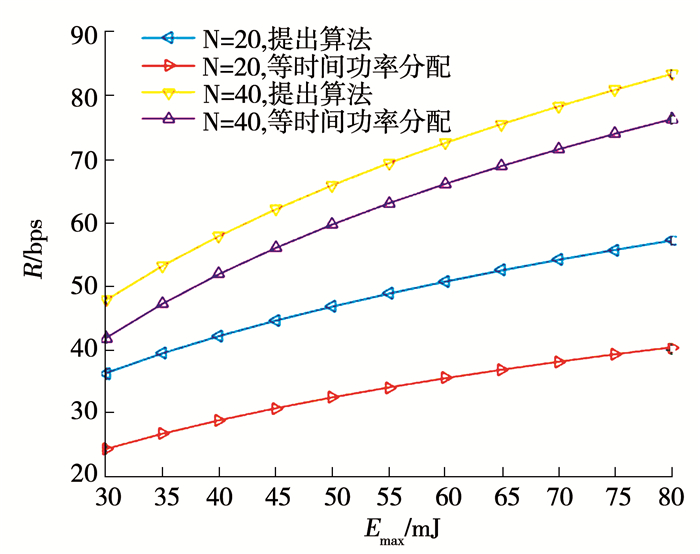点击查看原图

图 5 不同算法吞吐量随最小能量需求变化 Fig. 5 Throughput variation with minimum energy demand under different algorithms

图 6表示不同时隙数下吞吐量随最小能量的变化.可以看出，如果系统能量需求较大，即当E_min超过20 mJ时，传输速率R < 10 bps.因此为了提高传输速率应尽可能提高能量采集的效率.

Fig. 6
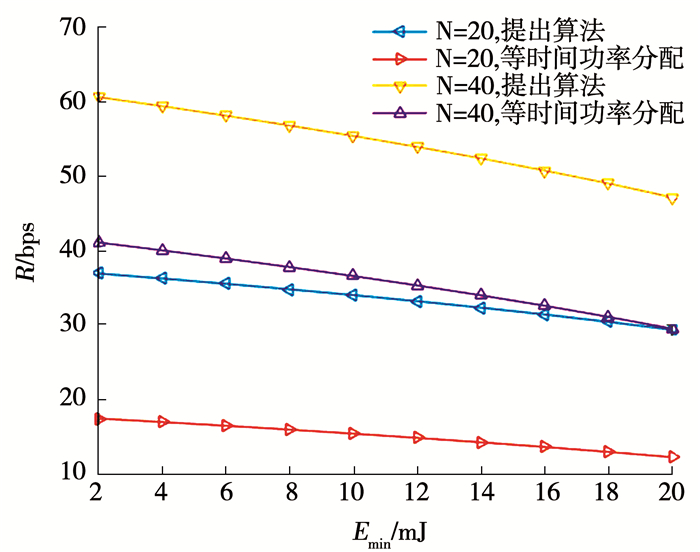点击查看原图

图 6 不同时隙数吞吐量随最小能量需求变化 Fig. 6 Throughput variation with minimum energy demand in different time slots

图 7给出系统吞吐率随时隙数的变化.可以看出随着时隙数增加，吞吐率会有显著提高，而等时间功率分配算法的吞吐率提高不明显.这是因为时隙数增加，频率选择性衰落提高，而本文算法具有信道自适应性，能够有效提高吞吐率.图 8给出了不同算法信息和能量的功率分配，可以看出本文算法当传输能量增加时，可分配的信息功率更大；而当能量需求增加时，信息功率会降低，更多的功率用于能量传输.

Fig. 7
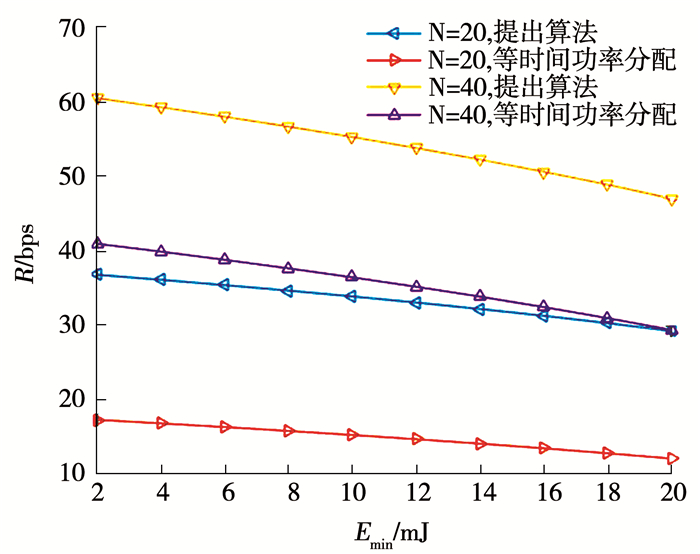点击查看原图

图 7 吞吐量随时隙数的变化 Fig. 7 Throughput variation with the number of time slots

Fig. 8
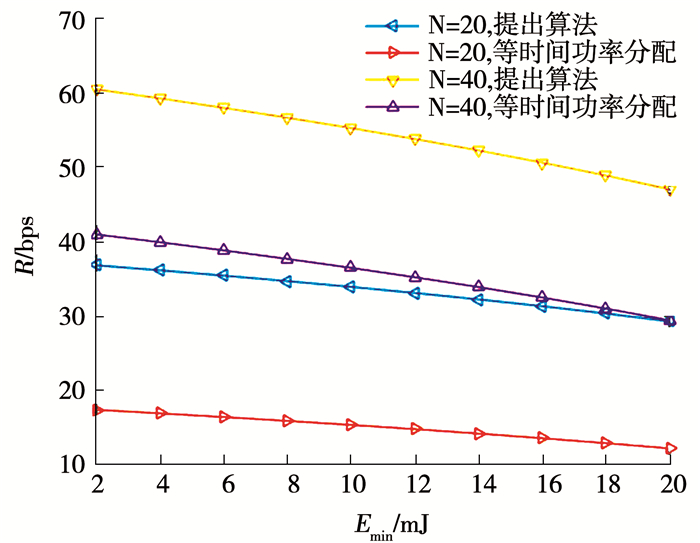点击查看原图

图 8 不同算法下信息和能量功率分配 Fig. 8 Information and energy power allocation under different algorithms

图 9是不同时隙数下信息和能量的功率分配.可以看出当时隙数从20增加到40时，分配给能量的功率相应会提升，这是因为当时隙数增加数本文算法选择信道最好的时隙传输信息，因此需要较少的信息功率就能获得较高的传输性能，相应的能量采集的功率会有所提升.图 10比较了不同无线携能通信方法的吞吐量，可以看出提出算法能够获得更高的吞吐量.基于时间转换和功率分流的无线携能通信为信息传输和能量传输分配固定的时隙和功率，不能够根据时间和信道条件的变化而自适应改变.而本文提出的多时隙无线携能通信能够在不同的时隙根据当前信道状况分配最优的功率，因此传输性能能够获得提高.

Fig. 9
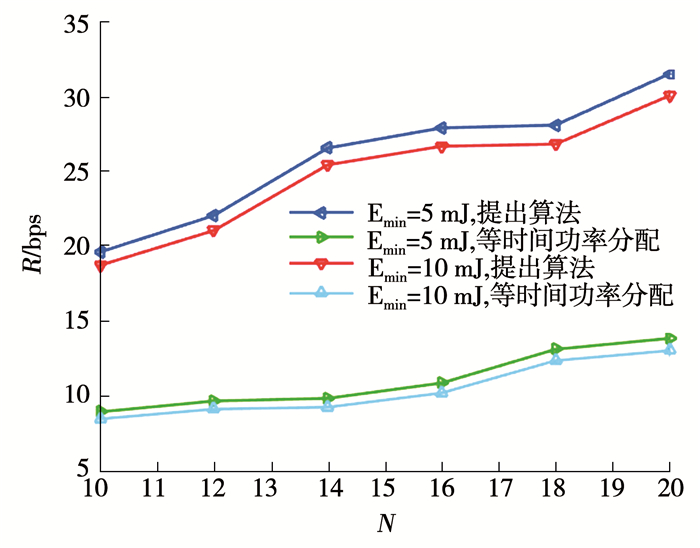点击查看原图

图 9 不同时隙数下信息和能量的功率分配 Fig. 9 Power allocation of information and energy in different time slots

Fig. 10
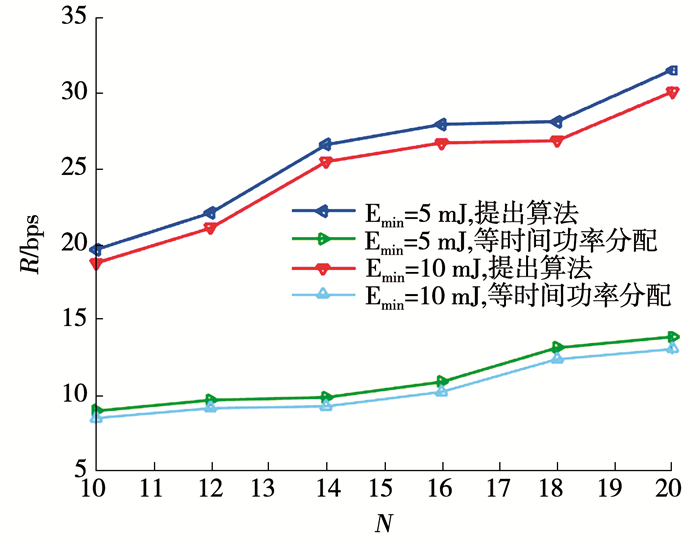点击查看原图

图 10 不同无线携能通信方法的吞吐量比较 Fig. 10 Throughput comparison among different SWIPT methods

4 结论本文提出一种多时隙无线携能通信系统，发射机在特定时隙传输信息或者能量，接收机在相应时隙解码信息和采集能量，采集能量用于补充传输能耗.通过联合优化时隙和功率分配，在保证系统能量需求的基础上最大化系统吞吐率.仿真结果表明，相比传统等时间功率分配算法，提出算法传输效率有明显提升.此外，应合理分配资源在信息和能量传输间获得性能折中.

参考文献
[1] JIANG Dingde, ZHANG Peng, LV Zhihan, et al. Energy-efficient multi-constraint routing algorithm with load balancing for smart city applications[J]. IEEE Internet of Things Journal, 2016, 3(6): 1437. DOI:10.1109/JI0T.2016.2613111

[2] HAN Tao, ANSARI N. Powering mobile networks with green energy[J]. IEEE Wireless Communications, 2014, 21(1): 90. DOI:10.1109/MWC.2014.6757901

[3] 王芳, 修素朴, 张咪, 等. 多射频源复合式能量收集系统优化设计[J]. 电子元件与材料, 2014, 33(9): 91.
WANG Fang, XIU Supu, ZHANG Mi, et al. Optimization design of multi-RF source hybrid energy harvesting system[J]. Electronic Components and Materials, 2014, 33(9): 91.

[4] RUAN Tingwen, CHU Zhengjun, ZHU Meiling. Energy-aware approaches for energy harvesting powered wireless sensor nodes[J]. IEEE Sensors Journal, 2017, 17(7): 2165. DOI:10.1109/JSEN.2017.2665680

[5] 韦保林, 韦雪明, 徐卫林, 等. 环境射频能量收集技术的研究进展及应用[J]. 通信技术, 2014, 47(4): 359.
WEI Baolin, WEI Xueming, XU Weilin, et al. Research progress and application of environmental RF energy harvesting technology[J]. Communication Technology, 2014, 47(4): 359. DOI:10.3969/j.issn.1002-0802.2014.04.004

[6] ZHANG Yiming, LU Ting, ZHAO Zhengming, et al. Selective wireless power transfer to multiple loads using receivers of different resonant frequencies[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6001. DOI:10.1109/TPEL.2014.2347966

[7] KHAN T A, YAZDAN A, HEATH R W Jr. Optimization of power transfer efficiency and energy efficiency for wireless-powered systems with massive MIMO[J]. IEEE Transactions on Wireless Communications, 2018, 17(11): 7159. DOI:10.1109/TWC.2018.2865727

[8] ALSABA Y, RAHIM S K A, LEOW C Y. Beamforming in wireless energy harvesting communications systems:A survey[J]. IEEE Communications Surveys & Tutorials, 2018, 20(2): 1329.

[9] ZHOU Xun, ZHANG Rui, HO C K. Wireless information and power transfer in multiuser OFDM systems[J]. IEEE Transactions on Wireless Communications, 2014, 13(4): 2282. DOI:10.1109/TWC.2014.030514.131479

[10] LIU Xin, LI Feng, NA Zhenyu. Optimal resource allocation in simultaneous cooperative spectrum sensing and energy harvesting for multichannel cognitive radio[J]. IEEE ACCESS, 2017, 5(3): 3801.

[11] YIN Sixing, QU Zhaowei, LI Shufang. Optimal multi-slot spectrum sensing in energy harvesting cognitive radio systems[J]. IEEE Global Communications Conference, 2014, 8(12): 793.

[12] HOANG D T, NIYATO D, WANG Ping, et al. Opportunistic channel access and RF energy harvesting in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(11): 2039. DOI:10.1109/JSAC.2014.141108

[13] ZHANG Rui, HO C K. MIMO broadcasting for simultaneous wireless information and power transfer[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 1989. DOI:10.1109/TWC.2013.031813.120224

[14] LIU Xin, CHEN Kunqi, YAN Junhua, et al. Optimal energy harvesting-based weighed cooperative spectrum sensing in cognitive radio network[J]. Mobile Networks and Applications, 2016, 21(6): 908. DOI:10.1007/s11036-016-0711-y

[15] KRIKIDIS I. SWIPT in 3-D bipolar ad hoc networks with sectorized antennas[J]. IEEE Communications Letters, 2016, 20(6): 1267. DOI:10.1109/LCOMM.2016.2557319

[16] VERMA D K, CHANG R Y, CHIEN F. Energy-assisted decode-and-forward for energy harvesting cooperative cognitive networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(3): 328. DOI:10.1109/TCCN.2017.2709759

[17] LI Ang, MASOUROS C. Energy-efficient SWIPT:From fully digital to hybrid analog-digital beamforming[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 3390. DOI:10.1109/TVT.2017.2782775

[18] JANG S, LEE H, KANG S, et al. Energy efficient SWIPT systems in multi-cell MISO networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(12): 8180. DOI:10.1109/TWC.2018.2874646

[19] ZHANG Qi, HUANG Xiaobin, LI Quanzhong, et al. Cooperative jamming aided robust secure transmission for wireless information and power transfer in MISO channels[J]. IEEE Transactions on Communications, 2015, 63(3): 906. DOI:10.1109/TCOMM.2015.2405063

[20] ALAGELI M, IKHLEF A, CHAMBERS J. SWIPT massive MIMO systems with active eavesdropping[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(1): 233. DOI:10.1109/JSAC.2018.2872370

[21] TIMOTHEOU S, KRIKIDIS I, KARACHONTZITIS S, et al. Spatial domain simultaneous information and power transfer for MIMO channels[J]. IEEE Transactions on Wireless Communications, 2015, 14(8): 4115. DOI:10.1109/TWC.2015.2416721

[22] ZHANG Meng, LIU Yuan, ZHANG Rui. Artificial noise aided secrecy information and power transfer in OFDMA systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 3085. DOI:10.1109/TWC.2016.2516528

[23] TIMOTHEOUI S, ZHENG Gan, MASOUROS C, et al. Exploiting constructive interference for simultaneous wireless information and power transfer in multiuser downlink systems[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1772. DOI:10.1109/JSAC.2016.2551618

[24] KHANDAKER M R A, WONG K. Robust secrecy beamforming with energy-harvesting eavesdroppers[J]. IEEE Wireless Communications Letters, 2015, 4(1): 10. DOI:10.1109/LWC.2014.2358586