龚维纬1,2,王伟1,雷大江2,关利超2,崔海龙2
(1.电子科技大学 机械与电气工程学院,成都 611731;2.中国工程物理研究院 机械制造工艺研究所,四川 绵阳621000)
摘要:
为探究研磨机床几何误差对金刚石刀具后刀面粗糙度的影响规律,建立研磨机床精度与刀具后刀面表面轮廓的数学模型. 借助多体系统理论对研磨机床的误差传递进行建模；基于样条滤波算法建立机床误差与刀具后刀面粗糙度之间的定量关系；分析主轴、摆轴的端面和径向跳动误差以及往复轴的直线度误差对刀具后刀面粗糙度的影响规律. 结果表明:主轴、摆轴和往复轴几何运动误差对刀具后刀面粗糙度的影响占比分别为98.18%、1.59%和0.23%；主轴的端面和径向跳动误差是影响后刀面粗糙度的主要因素,研究结果为研磨机床的设计制造与金刚石刀具研磨工艺的优化提供理论指导.
关键词: 研磨机床 几何误差 金刚石刀具 超精密加工 粗糙度
DOI：10.11918/201907147
分类号:TG729
文献标识码:A
基金项目:国家自然科学基金NSAF基金(U1830110)； 中央高校基本业务费(ZYGX2019J032)
Effects of lapping machine geometric errors on surface roughness of diamond cutting tools
GONG Weiwei1,2,WANG Wei1,LEI Dajiang2,GUAN Lichao2,CUI Hailong2
(1. School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China; 2. Institute of Machinery Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621000,Sichuan, China)
Abstract:
To investigate the effect of lapping machine geometric errors on flank face roughness of diamond cutting tools, a mathematic model of lapping machine geometric errors and surface profile of tool flank face is built. The error propagation of lapping machine is modeled based on the theory of multi-body system. And a quantified relationship between machine errors and roughness is established using the algorithm of spline filter. The influence principle of end face and radial errors of spindle and sway, and the straightness error of reciprocates on roughness are analyzed. The result shows that the influence proportion of spindle, sway and reciprocating geometric moving errors on roughness are 98.18%, 1.59% and 0.23% respectively, hence roughness of flank face is mainly affected by spindle end face and radial errors which offers a guidance to the design and manufacturing of lapping machine and optimization of lapping technics for diamond cutting tools.
Key words: lapping machine geometric error diamond cutting tool ultra-precision machining roughness
龚维纬, 王伟, 雷大江, 关利超, 崔海龙. 研磨机床几何误差对金刚石刀面粗糙度的影响[J]. 哈尔滨工业大学学报, 2020, 52(7): 29-34. DOI: 10.11918/201907147.
GONG Weiwei, WANG Wei, LEI Dajiang, GUAN Lichao, CUI Hailong. Effects of lapping machine geometric errors on surface roughness of diamond cutting tools[J]. Journal of Harbin Institute of Technology, 2020, 52(7): 29-34. DOI: 10.11918/201907147.
基金项目 国家自然科学基金NSAF基金(U1830110)；中央高校基本业务费(ZYGX2019J032) 作者简介 龚维纬(1995—)，男，硕士研究生;
王伟(1980—)，男，博士生导师 通信作者 王伟，wangwhit@163.com 文章历史 收稿日期: 2019-07-18
Abstract Full text Figures/Tables PDF
研磨机床几何误差对金刚石刀面粗糙度的影响
龚维纬1,2, 王伟1
, 雷大江2, 关利超2, 崔海龙2 1. 电子科技大学 机械与电气工程学院, 成都 611731;
2. 中国工程物理研究院 机械制造工艺研究所, 四川 绵阳621000
收稿日期: 2019-07-18
基金项目: 国家自然科学基金NSAF基金(U1830110)；中央高校基本业务费(ZYGX2019J032)
作者简介: 龚维纬(1995—)，男，硕士研究生; 王伟(1980—)，男，博士生导师
通信作者: 王伟，wangwhit@163.com
摘要: 为探究研磨机床几何误差对金刚石刀具后刀面粗糙度的影响规律，建立研磨机床精度与刀具后刀面表面轮廓的数学模型.借助多体系统理论对研磨机床的误差传递进行建模；基于样条滤波算法建立机床误差与刀具后刀面粗糙度之间的定量关系；分析主轴、摆轴的端面和径向跳动误差以及往复轴的直线度误差对刀具后刀面粗糙度的影响规律.结果表明：主轴、摆轴和往复轴几何运动误差对刀具后刀面粗糙度的影响占比分别为98.18%、1.59%和0.23%；主轴的端面和径向跳动误差是影响后刀面粗糙度的主要因素，研究结果为研磨机床的设计制造与金刚石刀具研磨工艺的优化提供理论指导.
关键词: 研磨机床 几何误差 金刚石刀具 超精密加工 粗糙度
Effects of lapping machine geometric errors on surface roughness of diamond cutting tools
GONG Weiwei1,2, WANG Wei1
, LEI Dajiang2, GUAN Lichao2, CUI Hailong2 1. School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China;
2. Institute of Machinery Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621000, Sichuan, China
Abstract: To investigate the effect of lapping machine geometric errors on flank face roughness of diamond cutting tools, a mathematic model of lapping machine geometric errors and surface profile of tool flank face is built. The error propagation of lapping machine is modeled based on the theory of multi-body system. And a quantified relationship between machine errors and roughness is established using the algorithm of spline filter. The influence principle of end face and radial errors of spindle and sway, and the straightness error of reciprocates on roughness are analyzed. The result shows that the influence proportion of spindle, sway and reciprocating geometric moving errors on roughness are 98.18%, 1.59% and 0.23% respectively, hence roughness of flank face is mainly affected by spindle end face and radial errors which offers a guidance to the design and manufacturing of lapping machine and optimization of lapping technics for diamond cutting tools.
Keywords: lapping machine geometric error diamond cutting tool ultra-precision machining roughness
金刚石刀具在超精密加工领域具有重要应用.金刚石刀具的微观几何形貌误差是影响加工质量的关键因素之一[1-2].目前，亟需高精度的金刚石刀具制造设备与技术.机械研磨法因具有较高精度、高研磨效率和低成本等优点，是目前主流的金刚石刀具研磨方法. Zong等[3-4]对圆弧刃金刚石刀具的机械研磨工艺做了大量研究，针对金刚石晶体的各项异性，分析了不同参数下以不同晶面作为刀具前、后刀面的研磨结果，给出了不同制造需求下的晶面选用原则.同时，借助化学氧化法[5]处理机械研磨后的金刚石刀具，其表面粗糙度算术均值Ra可达10 nm以下. Jirigalantu等[6]研究了一种用于金刚石刀具的刚性研磨技术，可将Ra优化至1.51 nm，但是，上述研究多关注研磨工艺参数的选取，缺乏包含研磨机床误差在内的综合研究.为研究机床误差对研磨精度的影响，需建立机床误差模型.常用的机床建模方法有误差矩阵法、二次关系法、变分法、机构学法和刚体运动学法，以上建模方法过程比较复杂，必须满足较严格的假设条件.刘又午[7]提出的基于多体系统理论的数控机床建模方法，可将几何误差和热误差统一在一个完整的模型中，该方法非常适合研磨机床的精度建模分析.朱春来[8]基于多体系统理论建立了某金刚石车刀研磨机误差模型，得到了11项对空间精度影响较大的误差源(如竖直方向的刀具进给误差)，但并未建立误差与刀具粗糙度的定量关系.总之，依靠研磨工艺优化的机械研磨法较为成熟，但已进入精度提升的瓶颈期；因此，本文从多体系统理论入手研究研磨机床几何误差对金刚石刀具后刀面粗糙度(简称“粗糙度”)的影响规律.
1 研磨机床模型多体系统理论已被广泛应用于多轴数控机床、机器人和多关节机械臂等的建模[9-11].研磨机床结构及运动示意图见图 1.其各体之间为刚性连接，每个刚体的运动学坐标关系都可以用一个4×4的矩阵表示[12-13].
Fig. 1
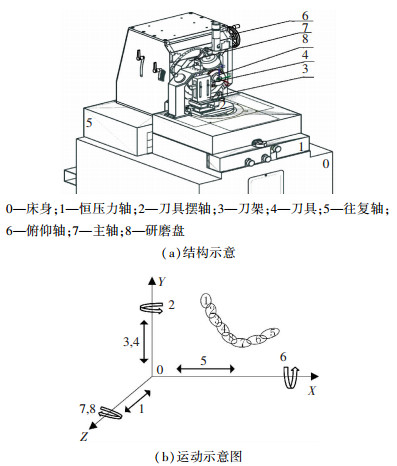图 1 研磨机床结构及运动 Fig. 1 Structure and movement of lapping machine 运动学原理表明，一个物体在空间共有6个自由度(3个平移自由度和3个旋转自由度)[14].
当物体A从空间一点移动x、y和z的距离且旋转α、β和γ的角度到另一点时，该运动变换矩阵为
$\mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{T}}_x}{\mathit{\boldsymbol{T}}_y}{\mathit{\boldsymbol{T}}_z}{\mathit{\boldsymbol{T}}_\alpha }{\mathit{\boldsymbol{T}}_\beta }{\mathit{\boldsymbol{T}}_\gamma }.$ (1)
其中，
${\mathit{\boldsymbol{T}}_x} = \left[ {\begin{array}{*{20}{c}}1&0&0&x\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}} \right],{\mathit{\boldsymbol{T}}_y} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&y\\0&0&1&0\\0&0&0&1\end{array}} \right];$
${\mathit{\boldsymbol{T}}_z} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&z\\0&0&0&1\end{array}} \right];$
${\mathit{\boldsymbol{T}}_\alpha } = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} \alpha }&0\\0&{{\rm{sin}}{\kern 1pt} {\kern 1pt} \alpha }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }&0\\0&0&0&1\end{array}} \right],$
${\mathit{\boldsymbol{T}}_\beta } = \left[ {\begin{array}{*{20}{c}}{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }&0&{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&0\\0&1&0&0\\{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }&0\\0&0&0&1\end{array}} \right],$
${\mathit{\boldsymbol{T}}_\gamma } = \left[ {\begin{array}{*{20}{c}}{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma }&0&0\\{{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }&0&0\\0&0&1&0\\0&0&0&1\end{array}} \right].$
实际上，空间运动物体在6个自由度方向都会有误差.以沿X轴平动为例，其存在定位误差为Δx，直线度误差为Δy、Δz，滚转角误差为Δα，偏摆角误差为Δβ、Δγ，将各项误差代入式(1)可得运动误差矩阵.由于角度误差较小，故可认为
$\begin{array}{l}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \alpha = {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \beta = {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \gamma = 1,\\{\rm{sin}}{\kern 1pt} {\kern 1pt} \Delta \alpha = \Delta \alpha ,{\rm{sin}}{\kern 1pt} {\kern 1pt} \Delta \beta = \Delta \beta ,{\rm{sin}}{\kern 1pt} {\kern 1pt} \Delta \gamma = \Delta \gamma .\end{array}$
略去各项二阶误差及以上的高阶小量，可得简化的运动误差矩阵为
$\Delta \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}}1&{ - \Delta \gamma }&{\Delta \beta }&{\Delta x}\\{\Delta \gamma }&1&{ - \Delta \alpha }&{\Delta y}\\{ - \Delta \beta }&{\Delta \alpha }&1&{\Delta z}\\0&0&0&1\end{array}} \right].$ (2)
以p，s分别代表静止和运动.静止时，研磨机床的恒压力轴与床身之间有一初始位置差距，在X、Y、Z向的分量为x01p、y01p、z01p.假设两者之间无其他静止误差，则静止坐标变换矩阵与静止误差变换矩阵分别为
${\mathit{\boldsymbol{T}}_{{\rm{01p}}}} = \left[ {\begin{array}{*{20}{c}}1&0&0&{{x_{{\rm{01p}}}}}\\0&1&0&{{y_{{\rm{01p}}}}}\\0&0&1&{{z_{{\rm{01p}}}}}\\0&0&0&1\end{array}} \right],\Delta {\mathit{\boldsymbol{T}}_{{\rm{01p}}}} = {\mathit{\boldsymbol{I}}_{4 \times 4}}.$
运动时，恒压力轴相对于床身有Z向的移动z01s，且存在6项运动误差：Δx01s、Δy01s、Δz01s、Δα01s、Δβ01s、Δγ01s, ，分别代入式(1)与式(2)，可得运动变换矩阵与运动误差变换矩阵分别为：
${\mathit{\boldsymbol{T}}_{{\rm{01s}}}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&{{z_{{\rm{01s}}}}}\\0&0&0&1\end{array}} \right],$
$\Delta {\mathit{\boldsymbol{T}}_{{\rm{01s}}}} = \left[ {\begin{array}{*{20}{c}}1&{ - \Delta {\gamma _{{\rm{0ls}}}}}&{\Delta {\beta _{{\rm{0ls}}}}}&{\Delta {x_{{\rm{0ls}}}}}\\{\Delta {\gamma _{{\rm{0ls}}}}}&1&{ - \Delta {\alpha _{{\rm{0ls}}}}}&{\Delta {y_{{\rm{0ls}}}}}\\{ - \Delta {\beta _{{\rm{0ls}}}}}&{\Delta {\alpha _{{\rm{0l}}}}}&1&{\Delta {z_{{\rm{0ls}}}}}\\0&0&0&1\end{array}} \right].$
则床身与恒压力轴间的实际变换矩阵为
${\mathit{\boldsymbol{T}}_{01}} = {\mathit{\boldsymbol{T}}_{{\rm{01p}}}}\Delta {\mathit{\boldsymbol{T}}_{{\rm{01p}}}}{\mathit{\boldsymbol{T}}_{{\rm{01s}}}}\Delta {\mathit{\boldsymbol{T}}_{{\rm{01s}}}}.$
同理，可推得其他部件间的实际变换矩阵：T12、T23、T34、T05、T56、T67、T78
理想情况下，刀具与研磨盘间为线接触，该线段在研磨盘坐标系下的矢量形式为
${\mathit{\boldsymbol{V}}_{\rm{w}}} = {\left[ {\begin{array}{*{20}{l}}{{x_{\rm{w}}}}&{{y_{\rm{w}}}}&{{z_{\rm{w}}}}&1\end{array}} \right]^{\rm{T}}}.$
将矢量由研磨盘坐标系映射到刀具坐标下, 可得此刻的研磨曲面形貌(矢量线段)
$S = {({\mathit{\boldsymbol{T}}_{01}}{\mathit{\boldsymbol{T}}_{12}}{\mathit{\boldsymbol{T}}_{23}}{\mathit{\boldsymbol{T}}_{34}})^{ - 1}}{\mathit{\boldsymbol{T}}_{05}}{\mathit{\boldsymbol{T}}_{56}}{\mathit{\boldsymbol{T}}_{67}}{\mathit{\boldsymbol{T}}_{78}}{\mathit{\boldsymbol{V}}_{\rm{w}}}.$ (3)
2 仿真分析朱春来[8]指出旋转轴轴向窜动、径跳和导轨直线度误差等是影响研磨精度主要因素，文献[15]认为刀具摆轴的定位误差和颠转误差及主轴的定位误差和颠转误差都会对研磨刀具的刀尖圆弧产生影响.研磨盘固结于主轴且对刀具表面起均化作用，故暂不考虑磨盘及磨粒的影响.对本文的卧式研磨机床，往复导轨定位误差影响刀具与研磨盘在圆弧切线方向的接触位置，在不考虑研磨盘及磨粒的情况下，导轨定位误差对研磨精度影响可忽略不计.故本文忽略了几何误差中的偏摆等角位移误差和导轨的定位误差，将旋转轴轴向定位误差转化为端面跳动，将其水平和竖直方向的直线度误差转化为径向跳动，研究主要运动部件中高速主轴和摆轴的端跳、径跳误差以及往复轴直线度误差对粗糙度的影响，如表 1所示.
表 1
表 1 主要运动部件误差 Tab. 1 Errors of main moving parts 部件 定位误差 直线度误差 端面跳动 径向跳动 主轴 Δz67 Δx67，Δy67 Δz67
摆轴 Δy12 Δz12，Δx12 Δy12
往复轴 Δx05 Δy05，Δz05
表 1 主要运动部件误差 Tab. 1 Errors of main moving parts
图 2(a)为使用反向法并分离标准球圆度误差后测得的研磨机床A主轴和摆轴的端跳、径跳数据；图 2(b)为往复导轨的直线度误差测试数据.
Fig. 2
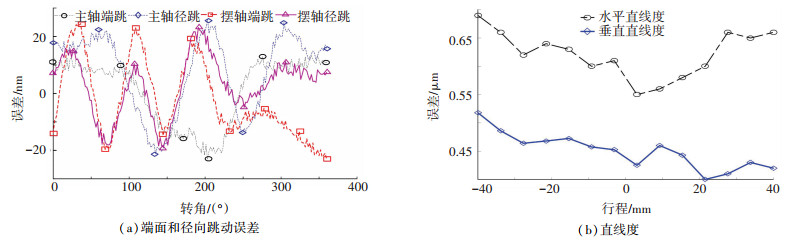图 2 研磨机床几何误差 Fig. 2 Geometric errors of lapping machine 2.1 主轴端面和径向跳动误差对粗糙度的影响主轴端面和径向跳动误差对粗糙度的影响见图 3.
Fig. 3
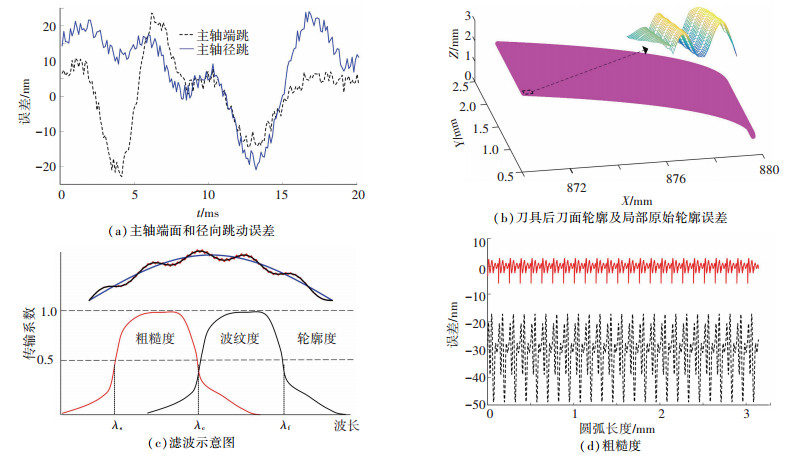图 3 主轴端面和径向跳动误差对刀具后刀面粗糙度的影响 Fig. 3 Effects of spindle end face and radial errors on flank face roughness 取主轴转速3 000 r/min(T=20 ms)，图 3(a)为按主轴实测数据频率和峰谷值特征构建的幅值50 nm的端面跳动和径向跳动误差.将误差代入式(3)可得主轴误差影响下的刀具后刀面表面形貌，如图 3(b)所示，其轮廓大致为圆柱面，减去公称形状可得到刀具后刀面局部区域(取样点数50×20)原始轮廓误差.
如图 3(c)所示，针对高精度的金刚石刀具，按照相关文献及国家标准[16-17]，长波截止波长λf取0.25~0.80mm，短波截止波长λc则为λf的1/10；本文不涉及高频环境噪声，故λs=0. 图 3(d)为使用样条滤波算法，对靠近刀尖处圆弧(下同)滤波得到的粗糙度轮廓中线(波纹度)和粗糙度轮廓误差(粗糙度)；在幅值50 nm的主轴端面和径向跳动误差影响下，刀具后刀面粗糙度算术平均偏差值为Ra=1.15 nm.
2.2 摆轴端面和径向跳动误差对粗糙度的影响按摆轴实测数据特征构建误差幅值50 nm的端面跳动与径向跳动误差，代入式(3)并减去公称形状后可得到由摆轴误差影响下的刀具后刀面局部轮廓误差. 图 4为滤波后的粗糙度轮廓中线和粗糙度；在幅值50 nm的摆轴端面和径向跳动误差影响下，刀具后刀面Ra=0.001 14 nm.
Fig. 4
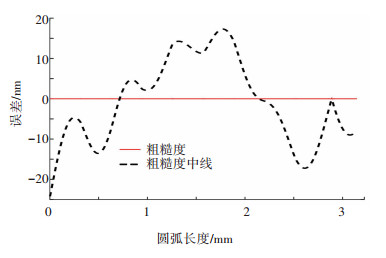图 4 摆轴端面径向跳动误差影响下的粗糙度 Fig. 4 Roughness influenced by sway end face and radial errors 2.3 往复轴直线度误差对粗糙度的影响按往复轴实测数据特征构建直线度误差100 nm/±40 mm的随机直线度误差，将其分解到水平(Z)和竖直(Y)方向可得往复轴的水平直线度误差和垂直直线度误差，再代入式(3)可得到仅有往复轴误差情况下的刀具后刀面轮廓. 图 5为使用样条滤波算法得到的粗糙度轮廓中线和粗糙度轮廓误差；在幅值100 nm的往复轴直线度误差影响下，刀具后刀面Ra=0.001 71 nm.
Fig. 5
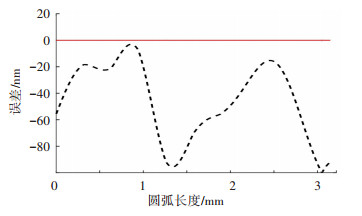图 5 往复轴直线度误差影响下的粗糙度 Fig. 5 Roughness influenced by reciprocating straightness errors 2.4 耦合误差对粗糙度的影响为进一步探究各个轴的误差对粗糙度的影响程度，下面分析耦合误差对刀具后刀面粗糙度的影响.
取主轴端面、径向跳动误差50 nm，摆轴端面、径向跳动误差50 nm，往复轴直线度误差100 nm.将各个轴的误差代入式(3)得到耦合误差影响下的刀具后刀面轮廓，减去公称形状后得原始轮廓误差，再滤波得到粗糙度轮廓中线和粗糙度，如图 6所示；耦合误差影响下的刀具后刀面Ra=1.93 nm.
Fig. 6
图 6 耦合误差影响下的粗糙度 Fig. 6 Roughness influenced by coupled errors 2.5 各轴的误差对刀具后刀面粗糙度的影响占比该问题本质上是一个多元函数问题，即
$R = f({x_1},{x_2},{x_3}).$
其中，R为粗糙度，x1、x2和x3分别为主轴、摆轴和往复轴的几何误差.
将粗糙度对各个变量的一阶偏导数定义为该误差的影响率Ki，即
${K_i} = \partial R/\partial {x_i},(i = 1,2,3).$
各影响率的绝对值在该组中所占比例定义为该误差对粗糙度的影响因子Ii：
${I_i} = |{K_i}|/\sum\limits_{j = 1}^3 | {K_j}|,(i = 1,2,3).$ (4)
取主轴、摆轴端面和径向跳动误差分别为50、100、150、200、250 nm；往复直线度误差分别为100、150、200、250、300 nm.实验包含3因素5水平，采用控制变量法设计了如表 2的各组实验.为减小每次实验的随机性影响，将每个实验重复100次，以100次实验得到的粗糙度算术均值作为该组误差影响下的粗糙度.
表 2
表 2 粗糙度计算值 Tab. 2 Roughness calculation results ? nm实验组 主轴误差 摆轴误差 往复轴误差 Ra
1 50 50 100 2.10
2 100 50 100 4.27
3 150 50 100 6.34
4 200 50 100 8.60
5 250 50 100 10.80
6 50 100 100 2.03
7 50 150 100 2.10
8 50 200 100 2.19
9 50 250 100 2.20
10 50 50 150 2.22
11 50 50 200 1.99
12 50 50 250 2.09
13 50 50 300 2.18
表 2 粗糙度计算值 Tab. 2 Roughness calculation results ?
图 7为粗糙度随各轴误差变化的离散点和使用最小二乘法拟合得到的直线.
Fig. 7
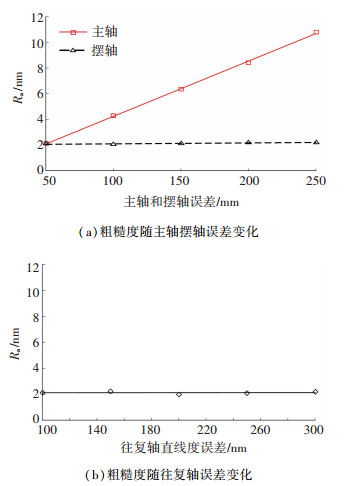图 7 粗糙度随各个轴的误差变化趋势 Fig. 7 Variation of roughness with errors of axes 从图 7(a)可知，粗糙度随主轴端面和径向跳动误差幅值的增大而增大，其拟合直线的斜率为K1=0.043 1；摆轴误差变化对粗糙度的影响较小，其拟合直线斜率为K2=0.000 7.由图 7(b)可得，往复轴直线度误差对粗糙度影响亦较小，其拟合直线的斜率为K3=0.000 1.则任意误差下对应的后刀面粗糙度算术平均值Ra可由式(5)近似得到
${R_{\rm{a}}} = {R_{{\rm{a0}}}} + {K_1}\Delta {x_1} + {K_2}\Delta {x_2} + {K_3}\Delta {x_3}.$ (5)
其中，Ra0为表 2中的某组Ra值，Δx1、Δx2和Δx3为与该组误差对应的变化量.
由式(4)可得主轴、摆轴的端面和径向跳动误差以及往复轴的直线度误差对粗糙度的影响占比分别为98.18%、1.59%和0.23%.
3 研磨实例为验证仿真分析的正确性，在A和B两台研磨机床上分别对编号为a1、a2和b1、b2的4把同材质金刚石刀具进行同工艺参数的研磨实验.研磨机床A主轴端面和径向跳动为49 nm，摆轴端面和径向跳动为43 nm，往复轴直线度为150 nm；研磨机床B主轴端面和径向跳动为96 nm，摆轴端面和径向跳动为80 nm，往复轴直线度为150 nm.由式(5)可得两台机床对应的后刀面粗糙度理论值分别为Ra, A=2.06 nm，Ra, B=4.11 nm. 图 8为使用原子力显微镜测得的4把刀具后刀面表面形貌，其表面均呈现出与图 3(b)仿真计算类似的沟壑条纹，Ra的测量结果分别为2.28、2.30、4.31和4.21 nm，相对误差分别为9.64%、10.40%、4.64%和2.43%.
Fig. 8
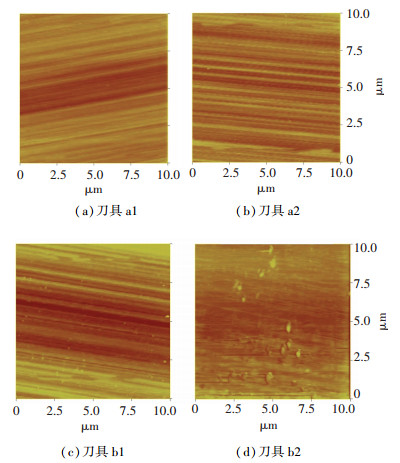图 8 后刀面粗糙度 Fig. 8 Flank face roughness 对比仿真与实验结果可知，计算值略小于实验值，这是因为实际研磨过程还包括其他部件的几何误差以及机床振动、环境噪声等因素的影响.仿真与实验结果间的最大相对误差为10%左右，说明了后刀面轮廓数学模型的有效性和仿真分析的正确性.
4 结论1) 本文针对某一研磨机床，借助多体系统理论和拓扑理论，建立了该研磨机床的精度传递模型，通过理论推导与仿真分析首次建立了机床主要部件几何误差与刀具后刀面粗糙度的定量关系.
2) 仿真计算结果略小于实验值，这是因为实际研磨过程还包括其他部件的等几何误差以及机床振动、环境噪声等因素的影响.
3) 在不考虑其他非核心运动部件误差、振动及环境因素影响的条件下，该型研磨机床的主轴、摆轴端面和径向跳动误差以及往复轴的运动直线度误差对粗糙度的影响占比分别为98.18%、1.59%和0.23%，表明主轴的端面和径向跳动误差是影响粗糙度的关键因素，该结论可为研磨机床的设计制造和刀具研磨工艺的优化提供理论支撑.
参考文献
[1] QIU Zhongjun, FANG Fengzhou, DING Liyu, et al. Investigation of diamond cutting tool lapping system based on on-machine image measurement[J]. The International Journal of Advanced Manufacturing Technology, 2011, 56(1): 79. DOI:10.1007/s00170-011-3168-y
[2] WYEN C F, KNAPP W G, WEGENER K. A new method for the characterisation of rounded cutting flanks[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59: 899. DOI:10.1007/s00170-011-3555-4
[3] ZONG Wenjun, SUN Tao, LI Di, et al. Design criterion for crystal orientation of diamond cutting tool[J]. Diamond and Related Materials, 2009, 18(4): 642. DOI:10.1016/j.diamond.2008.11.003
[4] ZONG Wenjun, LI Zengqiang, SUN Tao, et al. The basic issues in design and fabrication of diamond-cutting tools for ultra-precision and nanometric machining[J]. International Journal of Machine Tools and Manufacture, 2010, 50(4): 411. DOI:10.1016/j.ijmachtools.2009.10.015
[5] 宗文俊, 李增强, 胡振江, 等. 天然金刚石晶体的真空热化学腐蚀工艺[J]. 哈尔滨工业大学学报, 2013, 45(3): 61.
ZONG Wenjun, LI Zengqiang, HU Zhenjiang, et al. Thermo-chemical erosion of natural diamond crystals under vacuum atmosphere[J]. Journal of Harbin Institute of Technology, 2013, 45(3): 61. DOI:10.11918/j.issn.0367-6234.2013.03.011
[6] JIRIGALANTU A, BAYANHESHIG, QI Xiaodong. The research of rigid lapping technique on diamond grating ruling tool[J]. Advanced Materials Research, 2011, 179/180: 641. DOI:10.4028/www.scientific.net/AMR.179-180.641
[7] 刘又午. 多体动力学的休斯敦方法及其发展[J]. 中国机械工程, 2000, 11(6): 601.
LIU Youwu. Development of Huston's method on multi-body dynamics[J]. Journal of China Mechanical Engineering, 2000, 11(6): 601. DOI:10.3321/j.issn:1004-132X.2000.06.001
[8] 朱春来.金刚石刀具机械研磨机床误差分析及研磨机理研究[D].天津: 天津大学, 2013
ZHU Chunlai. Analysis on diamond tool machine error and study of grinding mechanism[D]. Tianjin: Tianjin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015017719.htm
[9] CAI Ligang, ZHANG Ziling, CHENG Qiang, et al. An approach to optimize the machining accuracy retainability of multi-axis NC machine tool based on robust design[J]. Precision Engineering, 2016, 43: 370. DOI:10.1016/j.precisioneng.2015.09.001
[10] TIAN Wenjie, HE Baiyan, HUANG Tian. Universal geometric error modeling of the CNC machine tools based on the screw theory[J]. Proceedings of SPIE: The International Society for Optical Engineering, 2011, 7997(2): 357. DOI:10.1117/12.894925
[11] FU Guoqiang, FU Jianzhong, XU Yuetong, et al. Accuracy enhancement of five-axis machine tool based on differential motion matrix: geometric error modeling, identification and compensation[J]. International Journal of Machine Tools & Manufacture, 2015(89): 170. DOI:10.1016/j.ijmachtools.2014.11.005
[12] 要小鹏, 殷国富, 方辉. 五轴机床误差建模与补偿解析新算法[J]. 四川大学学报(工程科学版), 2013, 45(5): 155.
YAO Xiaopeng, YIN Guofu, FANG Hui. A new synthesis error modeling and compensating algorithm of the five-axis machine tools[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(5): 155. DOI:10.15961/j.jsuese.2013.05.008
[13] ZHANG Ziling, CAI Ligang, CHENG Qiang, et al. A geometric error budget method to improve machining accuracy reliability of multi-axis machine tools[J]. Journal of Intellectual Manufacturing, 2016, 30: 495. DOI:10.1007/s10845-016-1260-8
[14] 孙惠娟, 殷国富, 方辉, 等. 五轴数控机床综合误差建模评价方法研究[J]. 四川大学学报(工程科学版), 2012, 44(6): 197.
SUN Huijuan, YIN Guofu, FANG Hui, et al. Research on integrated error modeling and evaluation method of five-axis machine tools[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 197. DOI:10.15961/j.jsuese.2012.06.011
[15] 李增强.圆弧刃金刚石刀具刀尖圆弧的机械研磨及其检测技术[D].哈尔滨: 哈尔滨工业大学, 2008.
LI Zengqiang. Mechanical lapping and measurement techniques of nose arc of rounded diamond cutting tools[D]. Harbin: Harbin Institute of Technology, 2008 http://d.wanfangdata.com.cn/thesis/D272071
[16] 雷大江, 岳晓斌, 崔海龙, 等. 金刚石刀具刀尖圆弧波纹度的测量及评价[J]. 光学精密工程, 2017, 25(10): 2697.
LEI Dajiang, YUE Xiaobin, CUI Hailong, et al. Measurement and evaluation of tool tip arc waviness of diamond tool[J]. Optics and Precision Engineering, 2017, 25(10): 2697. DOI:10.3788/OPE.-20172510.2697
[17] 全国产品几何技术规范标准化技术委员会.产品几何技术规范(GPS)表面结构轮廓法表面波纹度词汇: GB/T 16747—2009.[S].北京: 中国标准出版社, 2009
Dimensionaland Geometrical Product Specifications. Geometrical product specification (GPS)-Surface texture: profile method surface waviness terms: GB/T 16747—2009[S]. Beijing: Standards Press of China, 2009
