一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法

范千,陈振健,夏樟华

(福州大学 土木工程学院, 福州 350116)



摘要:

为克服基本樽海鞘群算法（SSA）存在的收敛速度慢、易陷入局部最优等不足,提出了一种基于折射反向学习和自适应控制因子的新型改进樽海鞘群算法（RCSSA）.首先,采用折射反向学习机制在每一次个体的求解中计算折射反向解,极大地提高了算法收敛精度和速度.然后,将原SSA算法中引导者的自适应控制因子引入跟随者的位置更新中,有效地控制整个搜索过程并增加了算法的局部开发能力.为验证所提RCSSA算法的优化性能,采用了7个单峰、16个多峰基准测试函数以及1个工程设计问题对其进行测试.试验中,先引入两种单策略改进的SSA算法来验证所提算法的有效性,再加入鲸鱼优化算法等5个先进的智能优化算法与之进行对比,进一步验证所提算法的优越性.研究结果表明:无论对于低维度还是高维度基准优化问题,所提算法都能有效地增强原SSA算法的开发和探索能力；并且RCSSA算法在整体优化性能方面要优于其他大多数群智能算法.

关键词:  樽海鞘群算法  折射反向学习  自适应控制因子  智能优化算法  基准函数

DOI：10.11918/201909176

分类号:TP301.6

文献标识码:A

基金项目:国家自然科学基金(41404008)；福建省交通运输科技项目(202103)；厦门市建设局科技项目(XJK2020-1-7)；福州大学贵重仪器设备开放测试基金(2020T037)



A modified salp swarm algorithm based on refracted opposition-based learning mechanism and adaptive control factor

FAN Qian,CHEN Zhenjian,XIA Zhanghua

(College of Civil Engineering, Fuzhou University, Fuzhou 350116, China)

Abstract:

To solve the problems that the basic salp swarm algorithm (SSA) converges slowly and is easy to fall into the local optimum, a new modified SSA based on refracted opposition-based learning (ROBL) and adaptive control factor (RCSSA) was proposed. First, the ROBL mechanism was used to calculate the refracted opposite solution of individual solution, which greatly improved the convergence accuracy and speed of the algorithm. Then, the adaptive control factor of the leader in SSA was introduced into the position update of the follower, which could effectively control the entire search process and increase the local exploitation ability. To verify the optimization performance of the proposed algorithm, seven unimodal, 16 multimodal benchmark functions, and one engineering design problem were utilized to investigate the algorithm. In the experiment, two SSAs improved by single strategy were introduced to verify the proposed algorithm, and five state-of-the-art intelligent optimization algorithms such as whale optimization algorithm were added to further verify the superiority of the algorithm. Research results show that the addition of ROBL mechanism and adaptive control factor could effectively enhance the exploitation and exploration abilities of the basic SSA for both low-dimensional and high-dimensional benchmark optimization problems, and the optimization performance of RCSSA was better than most other intelligent algorithms.

Key words:  salp swarm algorithm  refracted opposition-based learning  adaptive control factor  intelligent optimization algorithm  benchmark functions


范千, 陈振健, 夏樟华. 一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法[J]. 哈尔滨工业大学学报, 2020, 52(10): 183-191. DOI: 10.11918/201909176.
FAN Qian, CHEN Zhenjian, XIA Zhanghua. A modified salp swarm algorithm based on refracted opposition-based learning mechanism and adaptive control factor[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 183-191. DOI: 10.11918/201909176.
基金项目 国家自然科学基金(41404008);福建省交通运输科技项目(202103);厦门市建设局科技项目(XJK2020-1-7);福州大学贵重仪器设备开放测试基金(2020T037) 作者简介 范千(1981—)，男，博士，副教授 通信作者 范千，fanqian@fzu.edu.cn 文章历史 收稿日期: 2019-09-23



Abstract            Full text            Figures/Tables            PDF


一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法
范千, 陈振健, 夏樟华     
福州大学 土木工程学院，福州 350116

收稿日期: 2019-09-23
基金项目: 国家自然科学基金(41404008);福建省交通运输科技项目(202103);厦门市建设局科技项目(XJK2020-1-7);福州大学贵重仪器设备开放测试基金(2020T037)
作者简介: 范千(1981—)，男，博士，副教授
通信作者: 范千，fanqian@fzu.edu.cn


摘要: 为克服基本樽海鞘群算法(SSA)存在的收敛速度慢、易陷入局部最优等不足，提出了一种基于折射反向学习和自适应控制因子的新型改进樽海鞘群算法(RCSSA).首先，采用折射反向学习机制在每一次个体的求解中计算折射反向解，极大地提高了算法收敛精度和速度.然后，将原SSA算法中引导者的自适应控制因子引入跟随者的位置更新中，有效地控制整个搜索过程并增加了算法的局部开发能力.为验证所提RCSSA算法的优化性能，采用了7个单峰、16个多峰基准测试函数以及1个工程设计问题对其进行测试.试验中，先引入两种单策略改进的SSA算法来验证所提算法的有效性，再加入鲸鱼优化算法等5个先进的智能优化算法与之进行对比，进一步验证所提算法的优越性.研究结果表明：无论对于低维度还是高维度基准优化问题，所提算法都能有效地增强原SSA算法的开发和探索能力；并且RCSSA算法在整体优化性能方面要优于其他大多数群智能算法.
关键词: 樽海鞘群算法    折射反向学习    自适应控制因子    智能优化算法    基准函数    
A modified salp swarm algorithm based on refracted opposition-based learning mechanism and adaptive control factor
FAN Qian, CHEN Zhenjian, XIA Zhanghua     
College of Civil Engineering, Fuzhou University, Fuzhou 350116, China



Abstract: To solve the problems that the basic salp swarm algorithm (SSA) converges slowly and is easy to fall into the local optimum, a new modified SSA based on refracted opposition-based learning (ROBL) and adaptive control factor (RCSSA) was proposed. First, the ROBL mechanism was used to calculate the refracted opposite solution of individual solution, which greatly improved the convergence accuracy and speed of the algorithm. Then, the adaptive control factor of the leader in SSA was introduced into the position update of the follower, which could effectively control the entire search process and increase the local exploitation ability. To verify the optimization performance of the proposed algorithm, seven unimodal, 16 multimodal benchmark functions, and one engineering design problem were utilized to investigate the algorithm. In the experiment, two SSAs improved by single strategy were introduced to verify the proposed algorithm, and five state-of-the-art intelligent optimization algorithms such as whale optimization algorithm were added to further verify the superiority of the algorithm. Research results show that the addition of ROBL mechanism and adaptive control factor could effectively enhance the exploitation and exploration abilities of the basic SSA for both low-dimensional and high-dimensional benchmark optimization problems, and the optimization performance of RCSSA was better than most other intelligent algorithms.
Keywords: salp swarm algorithm    refracted opposition-based learning    adaptive control factor    intelligent optimization algorithm    benchmark functions    
近年来，优化问题在不同的学科和工程领域受到越来越多的关注，其主要分为三个类别：约束优化、无约束优化和约束工程优化问题^[1].在优化过程中，有必要在合理的时间内和复杂的约束下找到给定问题的最优解，因此如何构建有效的寻优策略是一个重要的研究方向.随着计算机技术的蓬勃发展，越来越多的群智能优化算法被相继提出.目前，常见的群智能算法有差分进化算法^[2]、粒子群算法^[3]、果蝇优化算法^[4]、灰狼优化算法^[5]、鲸鱼优化算法^[6]等.不同于传统优化算法，这些新型算法具有参数设置简单、无衍生机制、鲁棒性强等优点^[7]，已经被应用于多个研究领域.

樽海鞘群算法(Salp Swarm Algorithm, SSA)是Mirjalili等在2017年提出的一种新型的群体智能优化算法^[8]，该算法模仿了樽海鞘群体在海洋中的群体觅食行为.试验表明，与其它元启发式算法相比，SSA算法能够有效改进待优化问题的初始解并且能收敛到全局最优.因此原SSA算法被应用到各个学科优化问题的研究中，如：时差定位的非线性问题求解^[9]，燃料电池的最佳参数提取^[10]，非线性高光谱图像的处理^[11]等.而为了进一步提高SSA的性能，不同的学者也对其进行了改进：文献[12]将混沌映射与SSA算法结合，文献[13]提出了二进制SSA算法，文献[14]将粒子群算法与SSA算法进行混合等.这些算法在不同程度上提高了原SSA算法的性能.

根据“无免费午餐”(No-Free-Lunch，NFL)定理，没有一种算法能够适用于所有的优化问题^[15].因此，为了在实际应用中获得更好的结果，修改现有算法、开发新算法或混合不同种算法的研究工作是非常有价值的.针对原SSA算法存在的收敛速度慢、容易陷入局部最优等不足，本文提出一种新型的改进SSA算法，并将其称之为基于折射反向学习与自适应控制因子的改进樽海鞘群算法(Modified SSA Based on Refracted Oppositional Learning and Adaptive Control Factor, RCSSA).该算法首先在求解过程中引入折射反向学习机制，以提高算法收敛速度和精度，其次在部分位置更新中加入了原算法已有的自适应控制因子，进一步改进算法的探索性能.通过多组不同种类和维数的基准测试函数对RCSSA算法的性能进行详细测试，同时与其他算法进行对比分析，以验证所采用改进策略的可行性和有效性.

1 樽海鞘群优化算法SSA算法的灵感来自于樽海鞘群体在海洋中的游动和觅食行为.樽海鞘通过吸入和排出海水来推动自身游动，并以水中的浮游植物为食，如图 1所示.在觅食过程中，樽海鞘种群中的个体彼此相连并形成环状的长链.该樽海鞘长链可分为两部分：一部分为引导者，位于海鞘链的前端，负责探索食物的位置；另一部分樽海鞘为追随者，逐个相连，紧跟在引导者之后，如图 2所示.引导者以食物源为目标，不断更新自身位置，该数学模型为

Fig. 1
图 1 樽海鞘个体 Fig. 1 Individual salp


Fig. 2
图 2 樽海鞘群体觅食行为 Fig. 2 Foraging behavior of salp swarm


${x_{1, j}} = \left\{ {\begin{array}{*{20}{c}}{{F_j} + {c_1}\left( {\left( {u{b_j} - l{b_j}} \right){c_2} + l{b_j}} \right), {c_3} \ge 0.5;}\\{{F_j} - {c_1}\left( {\left( {u{b_j} - l{b_j}} \right){c_2} + l{b_j}} \right), {c_3} < 0.5.}\end{array}} \right.$ (1)

式中：x_{1, j}表示搜索空间第j维上第一个樽海鞘的位置，F_j表示食物的位置，ub_j和lb_j分别是搜索空间第j维的上界和下界，c₂和c₃是两个相互独立并服从[0, 1]均匀分布的随机数，c₁为算法中的控制因子，其值从2非线性递减至趋于0，如图 3所示，其计算公式如下

Fig. 3
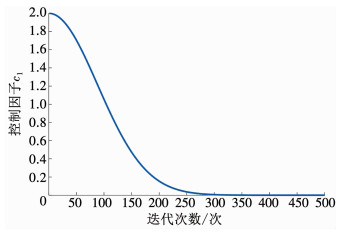图 3 控制因子c₁的变化曲线 Fig. 3 Curve of control factor c₁


${c_1} = 2{{\rm{e}}^{ - {{\left( {\frac{{4t}}{T}} \right)}^2}}}.$ (2)

式中：t表示当前迭代次数，T是预先设定好的最大迭代次数.

当引导者位置更新后，追随者随之移动，其位置更新的数学模型为

${x_{i, j}} = \frac{1}{2}\left( {{x_{i, j}} + {x_{i - 1, j}}} \right).$ (3)

式中:x_{i, j}表示搜索空间第j维上第i个樽海鞘的位置，且i≥2.

SSA算法包括探索和开发两个阶段.首先，探索阶段是从一组随机生成的解开始，其目标是在搜索空间中扩大搜索区域，以寻找全局最优解.接着，算法进入开发阶段，在前一阶段所得的搜索区域中进一步寻优，以提高最优解的准确性.其中，控制因子c₁对算法的收敛效果影响较大，有能够平衡算法的探索和开发能力：当c₁＞1时，算法进行全局探索；当c₁＜1时，算法对局部进行开发.在达到最大迭代次数时，算法终止并输出所得的最优结果.

2 改进的樽海鞘优化算法与其他元启发式算法类似，原SSA算法也存在收敛速度慢、容易陷入局部最优等缺点.为此本文从两个方面对其进行改进：首先，在种群个体更新时采用折射反向学习机制，从而提高种群多样性，避免算法陷入局部最优；其次，在追随者位置更新中引入自适应控制因子，进一步提高求解精度和收敛速度.

2.1 折射反向学习机制反向学习(Opposition-Based Learning, OBL)是由Tizhooshs提出的一种强大的优化机制^[16]，其通过计算当前解的反向解来扩大搜索范围，由此找出给定问题更好的候选解.将元启发式算法与OBL的结合，能够有效地提高算法寻优的精度^[17].但是OBL存在一定的缺点，如引入OBL的算法尽管在早期迭代能够加强算法的寻优性能，但在迭代后期OBL无法使算法跳出局部最优，从而导致收敛精度和速度均变差.

折射反向学习(Refracted Opposition-Based Learning, ROBL)是一种新型的算法改进机制，其本质是在反向学习的基础上，结合光的折射定律来寻找更优的候选解.近年被用于改进原粒子群优化算法^[18]与飞蛾扑火算法^[19]等，已被证明能够在不同程度上改善基本算法的性能.本文尝试将该机制引入SSA算法以提升其优化性能.ROBL的基本原理如图 4所示.

Fig. 4
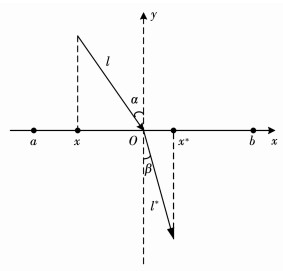图 4 折射反向学习机制 Fig. 4 ROBL mechanism


在图 4中，x轴上的解的搜索区间为[a，b]，y轴表示法线，入射光线和折射光线的长度分别为l和l^*，α和β分别为入射角和折射角，交点O是区间[a，b]的中点.由图中线段的几何关系，可得：

$\sin \alpha = \left( {\left( {a + b} \right)/2 - x} \right)/l, $ (4)

$sin\beta = \left( {{x^*} - \left( {a + b} \right)/2} \right)/{l^*}.$ (5)

由折射率的定义可知n=sin α/sin β，将其与以上二式结合得到

$n = \frac{{{l^*}\left( {\left( {a + b} \right)/2 - x} \right)}}{{l\left( {{x^*} - \left( {a + b} \right)/2} \right)}}.$ (6)

令k=l/l^*, 带入上式可得

$kn = \frac{{\left( {\left( {a + b} \right)/2 - x} \right)}}{{\left( {{x^*} - \left( {a + b} \right)/2} \right)}}.$ (7)

将式(7)进行变换，得到折射反向学习解的计算公式

${x^*} = \frac{{a + b}}{2} + \frac{{a + b}}{{2kn}} - \frac{x}{{kn}}.$ (8)

当k=1，n=1时，上式可转化为标准的反向学习公式

${x^*} = a + b - x.$ (9)

显然OBL仅为ROBL的一个特例.相对于OBL只能得到固定的候选解，ROBL可以通过调整参数获得动态的新候选解，这也将会提高算法跳出局部最优的概率.当优化问题的空间维度增加时，折射反向学习解可按下式计算

$x_{i, j}^* = \frac{{{a_j} + {b_j}}}{2} + \frac{{{a_j} + {b_j}}}{{2k}} - \frac{{{x_{i, j}}}}{k}.$ (10)

式中：x_{i, j}表示当前种群中第i个体在第j维上位置，x_{i, j}^*为x_{i, j}的折射反向解，a_j和b_j分别为搜索空间上第j维的最小值和最大值.

2.2 自适应控制因子在原SSA算法中，随着算法的迭代进化，樽海鞘群体中的引导者不断向食物源移动，其余追随者依次相连，逐渐向种群中适应度较优的引导者靠拢.然而，从式(3)中可看到，追随者的位置只跟自身和相邻个体的位置相关，其行为较为单一.因此，当种群中的引领者陷入局部最优时，追随者必然随之陷入局部最优，从而导致算法出现早熟收敛现象.

前文已经提到：控制因子c₁随着迭代次数的增加，从2非线性降低到趋于0.这样的变化有利于算法在迭代初期进行全局探索，在迭代后期能够在局部进行开发.为此，本文提出将控制因子c₁引入追随者的位置更新，此时追随者也能够与引导者一样，产生自适应更新，从而提高算法跳出局部最优的能力，并加快整体的收敛速度.新的追随者公式为

${x_{i, j}} = \frac{{{c_1}}}{2}\left( {{x_{i, j}} + {x_{i - 1, j}}} \right).$ (11)

其中c₁的表达式见式(2).

2.3 所提RCSSA算法综合上述策略对基本SSA算法进行改进后，得到的RCSSA算法实现流程如下：

Step1：设置算法参数：种群规模N，最大迭代次数T，搜索维数D，搜索范围[lb, ub]；随机生成樽海鞘种群；

Step2：计算每个个体的适应度值，将适应度值最小的个体位置作为食物源；

Step3：更新控制因子c₁，判断种群数是否超过N/2：超过则进入Step5，否则进入Step4；

Step4：更新随机数c₂、c₃，根据式(1)更新每个引导者个体的位置，同时采用式(10)计算其折射反向解，比较二者适应度大小，取较小的一个个体为新的位置，并进入Step6；

Step5：根据式(3)更新每个追随者个体的位置，采用引入控制因子c₁的式(11)计算其折射反向解，比较二者适应度大小，取较小的一个个体为新的位置；

Step6：比较食物源和当前樽海鞘最优个体的适应度大小，取较小的一个为新的食物源；

Step7：若当代迭代次数达到最大迭代次数T，则输出最优个体，即算法找到的最优解；否则，返回Step2.

3 仿真实验及分析 3.1 基准测试函数为了测试RCSSA在解决全局优化问题中的效果，本文从文献[6]中选取23个基准测试函数进行算法性能测试.根据函数特征将这23个测试函数分为三个不同类型：可缩放单峰、多峰函数以及固定维度多峰函数.其中，函数F₁~F₇属于维度可变单峰函数，其仅包含一个全局最优，因此这些函数能够测试算法的开发能力；而维度可变多峰函数(F₈~F₁₃)包含多个局部最优，不易找到全局最优，可用于验证算法的全局探索能力；固定维多峰函数(F₁₄~F₂₃)的极值点较多，但由于维度较低，寻优较容易，可用来测试算法的稳定性.这些函数的表达式、维度、搜索范围、理论最优值和类型如表 1所示.

表 1
表 1 基准测试函数 Tab. 1 Benchmark functions 函数 维度 范围 理论最优值 类型

${F_1}\left( x \right) = \sum\limits_{i = 1}^n {x_i^2} $ 30/100 [-100, 100] 0 单峰

${F_2}\left( x \right) = \sum\limits_{i = 1}^n {\left| {{x_i}} \right| - \prod\limits_{i = 1}^n {\left| {{x_i}} \right|} } $ 30/100 [-10, 10] 0 单峰

${F_3}\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {\sum {_{j = 1}^i} {x_j}} \right)}^2}} $ 30/100 [-100, 100] 0 单峰

${F_4}\left( x \right) = {\max _i}\left\{ {\left| {{x_i}} \right|, 1 \le i \le n} \right\}$ 30/100 [-100, 100] 0 单峰

${F_5}\left( x \right) = \sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right]} $ 30/100 [-30, 30] 0 单峰

${F_6}\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {\left| {{x_i} + 0.5} \right|} \right)}^2}} $ 30/100 [-100, 100] 0 单峰

${F_7}\left( x \right) = \sum\limits_{i = 1}^n {ix_i^4 + {\rm{rando}}\left[ {0, 1} \right]} $ 30/100 [-1.28, 1.28] 0 单峰

${F_8}\left( x \right) = \sum\limits_{i = 1}^n { - {x_i}\sin \left( {\sqrt {\left| {{x_i}} \right|} } \right)} $ 30/100 [-500, 500] -418.9829×D 多峰

${F_9}\left( x \right) = \sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right) + 10} \right]} $ 30/100 [-5.12, 5.12] 0 多峰

$\begin{array}{l} {F_{10}}\left( x \right) = - 20\exp \left( { - 0.2\sqrt {\frac{1}{n}\sum {_{i = 1}^nx_i^2} } } \right) - \exp \left( {\frac{1}{n}\sum {_{i = 1}^n\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} } \right) + \\ 20 + e \end{array}$ 30/100 [-32, 32] 0 多峰

${F_{11}}\left( x \right) = \frac{1}{{4\;000}}\sum\limits_{i = 1}^n {x_i^2 - \prod\limits_{i = 1}^n {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right)} } + 1$ 30/100 [-600, 600] 0 多峰

$\begin{array}{l} {F_{12}}\left( x \right) = \frac{\pi }{n}\left\{ {10{{\sin }^2}\left( {{\rm{ \mathsf{ π} }}{y_i}} \right) + \sum {_{i = 1}^{n - 1}{{\left( {{y_i} - 1} \right)}^2}\left[ {1 + 10{{\sin }^2}\left( {{\rm{ \mathsf{ π} }}{y_{i{\rm{ + 1}}}}} \right)} \right] + {{\left( {{y_n} - 1} \right)}^2}} } \right\}\\ + \sum\limits_{i = 1}^n {u\left( {{x_i}, 10, 100, 4} \right)} , {y_i} = 1 + \frac{{{x_i} + 1}}{4}, u\left( {{x_i}, a, k, m} \right) = \left\{ {\begin{array}{*{20}{c}} {k{{\left( {{x_i} - a} \right)}^m}, {x_i} > a}\\ {0, - a < {x_i} < a}\\ {k{{\left( { - {x_i} - a} \right)}^m}, {x_i} < a} \end{array}} \right. \end{array}$ 30/100 [-50, 50] 0 多峰

$\begin{array}{l} {F_{13}}\left( x \right) = 0.1\left\{ {{{\sin }^2}\left( {3{\rm{ \mathsf{ π} }}{x_i}} \right) + \sum {_{i = 1}^{n - 1}{{\left( {{x_i} - 1} \right)}^2}\left[ {1 + {{\sin }^2}\left( {3{\rm{ \mathsf{ π} }}{x_i}_{ + 1}} \right)} \right] + {{\left( {{x_n} - 1} \right)}^2}\left[ {1 + {{\sin }^2}\left( {2{\rm{ \mathsf{ π} }}{x_n}} \right)} \right]} } \right\} + \\ \sum\limits_{i = 1}^n {u\left( {{x_i}, 5, 100, 4} \right)} \end{array}$ 30/100 [-50, 50] 0 多峰

${F_{14}}\left( x \right) = {\left( {\frac{1}{{500}} + \sum {_{j = 1}^{25}} \frac{1}{{j + \sum {_{i = 1}^n} {{\left( {{x_i} - {a_{ij}}} \right)}^6}}}} \right)^{ - 1}}$ 2 [-65, 65] 1 多峰

${F_{15}}\left( x \right) = \sum\limits_{i = 1}^{11} {{{\left[ {{a_i} - \frac{{{x_1}\left( {b_i^2 + {b_i}{x_2}} \right)}}{{b_i^2 + {b_i}{x_3} + {x_4}}}} \right]}^2}} $ 4 [-5, 5] 0.000 30 多峰

${F_{16}}\left( x \right) = 4x_1^2 - 2.1x_1^4 + \frac{1}{3}x_1^6 + {x_1}{x_2} - 4x_2^2 + 4x_2^4$ 2 [-5, 5] -1.031 6 多峰

${F_1}_7\left( x \right) = {\left( {{x_2} - \frac{{5.1}}{{4{{\rm{ \mathsf{ π} }}^2}}}x_1^2 + \frac{5}{{\rm{ \mathsf{ π} }}}{x_1} - 6} \right)^2} + 10\left( {1 - \frac{1}{{8{\rm{ \mathsf{ π} }}}}} \right)\cos {x_1} + 10$ 2 [-5, 5] 0.398 多峰

$\begin{array}{l} {F_{18}}\left( x \right) = \left[ {1 + {{\left( {{x_1} + {x_2} + 1} \right)}^2}\left( {19 - 14{x_1} + 3x_1^2 - 14{x_2} + 6{x_1}{x_2} + 3x_2^2} \right)} \right] \times \\ \left[ {30 + {{\left( {2{x_1} - 3{x_2}} \right)}^2} \times \left( {18 - 32{x_1} + 12x_1^2 + 48{x_2} - 36{x_1}{x_2} + 27x_2^2} \right)} \right] \end{array}$ 2 [-2, 2] 3 多峰

${F_{19}}\left( x \right) = - \sum\limits_{i = 1}^4 {{c_i}\exp \left( { - \sum {_{j = 1}^3{a_{ij}}{{\left( {{x_j} - {p_{ij}}} \right)}^2}} } \right)} $ 3 [1, 3] -3.86 多峰

${F_{20}}\left( x \right) = - \sum\limits_{i = 1}^4 {{c_i}\exp \left( { - \sum {_{j = 1}^6{a_{ij}}{{\left( {{x_j} - {p_{ij}}} \right)}^2}} } \right)} $ 6 [0, 1] -3.32 多峰

${F_{21}}\left( x \right) = - \sum\limits_{i = 1}^5 {{{\left[ {\left( {X - {a_i}} \right){{\left( {X - {a_i}} \right)}^{\rm{T}}} + {c_i}} \right]}^{ - 1}}} $ 4 [0, 10] -10.153 2 多峰

${F_{22}}\left( x \right) = - \sum\limits_{i = 1}^7 {{{\left[ {\left( {X - {a_i}} \right){{\left( {X - {a_i}} \right)}^{\rm{T}}} + {c_i}} \right]}^{ - 1}}} $ 4 [0, 10] -10.402 8 多峰

${F_{23}}\left( x \right) = - \sum\limits_{i = 1}^{10} {{{\left[ {\left( {X - {a_i}} \right){{\left( {X - {a_i}} \right)}^{\rm{T}}} + {c_i}} \right]}^{ - 1}}} $ 4 [0, 10] -10.536 3 多峰



表 1 基准测试函数 Tab. 1 Benchmark functions


3.2 算法参数设置利用RCSSA算法对23个基准测试函数进行寻优求解，并与基本SSA、仅加入折射反向学习机制的SSA算法(RSSA)以及仅采用自适应控制因子的SSA算法(CSSA)进行对比，以验证所提综合改进策略的效果.此外，选择了5种群智能算法进行对比测试，这5种算法分别为：PSO^[3]，GWO^[5]，WOA^[6]，多元宇宙优化算法(MVO)^[20]和正弦余弦算法(SCA)^[21].这些算法已被证明具有较好的优化性能，并被应用到了不同的学科与工程领域.因此，将本文所提的RCSSA算法与之进行对比，可验证所提算法在优化性能方面是否具有优越性.

为了对比的公平性，将所有算法的参数设置为一致：迭代次数设为500，种群规模均设为30，控制因子初始值均设为2.其余算法参数按原论文进行取值，其中，RCSSA与RSSA中的缩放因子k=10 000.

3.3 RCSSA算法的性能测试 3.3.1 精度分析为防止随机性造成的误差，在相同条件下，将各算法在MATLAB2017a中独立运行30次，得到30维、100维函数的试验结果见表 2、表 3.表中的适应度平均值和标准差分别反映不同算法在给定独立运行次数下的收敛精度和稳定性，表中的加粗数据为最佳试验结果.

表 2
表 2 30维基准测试函数寻优结果对比 Tab. 2 Comparison of optimization results of 30-dimensional benchmark functions 函数 指标 SSA RSSA CSSA PSO GWO MVO WOA SCA RCSSA

F₁ 平均值 1.65×10^-7 4.49×10^-146 1.71×10^-217 1.61×10^-4 2.46×10^-27 1.22 7.27×10^-75 1.55×10¹ 0.00

标准差 1.77×10^-7 5.01×10^-147 0.00 3.20×10^-4 6.44×10^-27 3.33×10^-1 2.34×10^-74 4.17×10¹ 0.00

F₂ 平均值 2.36 9.79×10^-74 1.97×10^-109 8.09 8.84×10^-17 6.73 4.97×10^-50 2.56×10^-2 1.98×10^-173

标准差 1.87 8.40×10^-75 1.87×10^-110 8.00 5.42×10^-17 1.95×10¹ 2.71×10^-49 4.28×10^-02 0.00

F₃ 平均值 1.34×10³ 1.81×10^-145 2.86×10^-216 9.27×10¹ 9.13×10^-6 2.19×10² 4.52×10⁴ 8.92×10³ 0.00

标准差 8.33×10² 8.06×10^-146 0.00 3.39×10¹ 1.99×10^-5 7.98×10¹ 1.41×10⁴ 5.74×10³ 0.00

F₄ 平均值 1.18×10¹ 6.62×10^-74 1.29×10^-109 1.06 9.43×10^-7 1.89 5.27×10¹ 3.59×10¹ 1.27×10^-173

标准差 3.18 2.26×10^-75 3.28×10^-111 2.34×10^-1 1.15×10^-6 6.35×10^-1 2.48×10¹ 1.39×10¹ 0.00

F₅ 平均值 2.67×10² 2.86×10¹ 2.86×10¹ 1.09×10² 2.70×10¹ 2.37×10² 2.82×10¹ 7.50×10⁴ 2.85×10¹

标准差 4.90×10² 2.15×10^-2 3.88×10^-2 1.06×10² 7.68×10^-1 2.66×10² 5.14×10^-1 2.35×10⁵ 3.47×10^-2

F₆ 平均值 1.31×10^-7 5.72×10^-7 4.74×10^-7 1.44×10^-4 6.96×10^-1 1.28 4.50×10^-1 6.32×10¹ 1.88×10^-7

标准差 1.25×10^-7 2.08×10^-6 6.98×10^-7 1.69×10^-4 3.70×10^-1 3.15×10^-1 2.36×10^-1 1.62×10² 2.75×10^-7

F₇ 平均值 1.66×10^-1 6.57×10^-5 9.67×10^-5 3.97 1.92×10^-3 3.53×10^-2 6.20×10^-3 1.48×10^-1 5.89×10^-5

标准差 6.99×10^-2 6.10×10^-5 7.60×10^-5 6.04 8.32×10^-4 1.32×10^-2 6.83×10^-3 2.37×10^-1 4.61×10^-5

F₈ 平均值 -7.43×10³ -7.27×10³ -7.48×10³ -4.41×10³ -6.02×10³ -7.54×10³ -1.01×10⁴ -3.80×10³ -7.88×10³

标准差 4.84×10² 5.89×10² 8.52×10² 1.12×10³ 7.74×10² 6.28×10² 1.69×10³ 3.44×10² 1.45×10³

F₉ 平均值 5.50×10¹ 0.00 0.00 1.05×10² 1.76 1.13×10² 0.00 3.82×10¹ 0.00

标准差 2.38×10¹ 0.00 0.00 3.19×10¹ 2.98 2.80×10¹ 0.00 3.75×10¹ 0.00

F₁₀ 平均值 2.89 8.88×10^-16 8.88×10^-16 2.36×10^-1 1.01×10^-13 1.78 4.09×10^-15 1.58×10¹ 8.88×10^-16

标准差 1.90 0.00 0.00 5.17×10^-1 1.65×10^-14 6.14×10^-1 2.70×10^-15 7.78 0.00

F₁₁ 平均值 1.58×10^-2 0.00 0.00 9.96×10^-3 2.70×10^-3 8.57×10^-1 4.80×10^-3 9.26×10^-1 0.00

标准差 9.08×10^-3 0.00 0.00 9.49×10^-3 7.45×10^-3 9.30×10^-2 2.63×10^-2 3.54×10^-1 0.00

F₁₂ 平均值 6.56 1.51×10^-2 3.02×10^-2 1.04×10^-2 4.71×10^-2 2.56 2.41×10^-2 1.33×10⁴ 1.92×10^-2

标准差 3.76 3.11×10^-2 3.45×10^-2 3.16×10^-2 2.34×10^-2 1.77 2.09×10^-2 4.57×10⁴ 3.40×10^-2

F₁₃ 平均值 1.73×10¹ 2.22 2.58 5.55×10^-3 7.08×10^-1 2.21×10^-1 5.68×10^-1 5.15×10⁴ 2.48

标准差 1.58×10¹ 1.25 1.00 5.61×10^-3 2.19×10^-1 1.53×10^-1 3.23×10^-1 1.92×10⁵ 1.11



表 2 30维基准测试函数寻优结果对比 Tab. 2 Comparison of optimization results of 30-dimensional benchmark functions


表 3
表 3 100维基准测试函数寻优结果对比 Tab. 3 Comparison of optimization results of 100-dimensional benchmark functions 函数 指标 SSA RSSA CSSA PSO GWO MVO WOA SCA RCSSA

F₁ 平均值 1.31×10³ 1.58×10^-145 5.83×10^-217 2.35×10¹ 1.60×10^-12 1.69×10² 1.43×10^-72 1.07×10⁴ 0.00

标准差 3.24×10² 1.32×10^-146 0.00 7.24 1.15×10^-12 2.64×10¹ 4.67×10^-72 7.58×10³ 0.00

F₂ 平均值 4.71×10¹ 3.40×10^-73 6.57×10^-109 1.23×10² 4.68×10^-8 2.74×10²³ 2.93×10^-51 5.71 6.57×10^-173

标准差 8.01 1.65×10^-74 3.62×10^-110 2.92×10¹ 1.96×10^-8 1.39×10²⁴ 1.20×10^-50 3.70 0.00

F₃ 平均值 4.59×10⁴ 1.76×10^-144 3.09×10^-215 1.76×10⁴ 5.90×10² 6.70×10⁴ 1.14×10⁶ 2.34×10⁵ 0.00

标准差 2.14×10⁴ 8.48×10^-145 0.00 4.24×10³ 7.79×10² 8.86×10³ 3.09×10⁵ 5.95×10⁴ 0.00

F₄ 平均值 2.75×10¹ 6.79×10^-74 1.31×10^-109 1.22×10¹ 6.89×10^-1 5.68×10¹ 7.38×10¹ 8.93×10¹ 1.31×10^-173

标准差 3.82 9.52×10^-76 1.03×10^-111 1.46 5.90×10^-1 6.73 2.38×10¹ 2.49 0.00

F₅ 平均值 1.58×10⁵ 9.82×10¹ 9.82×10¹ 1.83×10⁴ 9.78×10¹ 1.45×10⁴ 9.81×10¹ 1.10×10⁸ 9.82×10¹

标准差 8.50×10⁴ 3.86×10^-2 3.51×10^-2 8.05×10³ 6.85×10^-1 1.25×10⁴ 2.40×10^-1 4.79×10⁷ 3.96×10^-2

F₆ 平均值 1.33×10³ 3.24 3.33 1.95×10¹ 1.02×10¹ 1.65×10² 4.68 1.14×10⁴ 3.20

标准差 3.44×10² 6.69×10^-1 5.72×10^-1 4.55 9.06×10^-1 2.77×10¹ 1.06 9.22×10³ 6.43×10^-1

F₇ 平均值 2.70 6.87×10^-5 1.02×10^-4 3.12×10² 7.87×10^-3 6.78×10^-1 3.85×10^-3 1.23×10² 7.12×10^-5

标准差 6.37×10^-1 5.78×10^-5 7.79×10^-5 1.18×10² 2.39×10^-3 1.54×10^-1 3.77×10^-3 6.85×10¹ 7.08×10^-5

F₈ 平均值 -2.14×10⁴ -2.07×10⁴ -2.21×10⁴ -1.11×10⁴ -1.61×10⁴ -2.30×10⁴ -3.46×10⁴ -7.05×10³ -2.36×10⁴

标准差 2.03×10³ 1.93×10³ 2.23×10³ 3.46×10³ 2.82×10³ 1.51×10³ 6.05×10³ 5.02×10² 4.02×10³

F₉ 平均值 2.46×10² 0.00 0.00 7.56×10² 9.94 7.07×10² 3.79×10^-15 2.45×10² 0.00

标准差 4.11×10¹ 0.00 0.00 7.89×10¹ 7.75 8.61×10¹ 2.08×10^-14 1.10×10² 0.00

F₁₀ 平均值 9.87 8.88×10^-16 8.88×10^-16 3.58 1.11×10^-7 8.61 4.80×10^-15 1.92×10¹ 8.88×10^-16

标准差 1.09 0.00 0.00 3.03×10^-1 4.09×10^-8 6.49 2.85×10^-15 3.83 0.00

F11 平均值 1.24×10¹ 0.00 0.00 4.18×10^-1 3.68×10^-3 2.49 2.34×10^-2 8.08×10¹ 0.00

标准差 3.83 0.00 0.00 7.60×10^-2 9.65×10^-3 2.86×10^-1 8.94×10^-2 5.94×10¹ 0.00

F₁₂ 平均值 3.57×10¹ 9.24×10^-2 1.67×10^-1 4.62 3.15×10^-1 2.00×10¹ 4.25×10^-2 3.10×10⁸ 1.63×10^-1

标准差 1.30×10¹ 2.62×10^-2 3.57×10^-2 1.44 7.65×10^-2 7.78 1.59×10^-2 1.79×10⁸ 4.53×10^-2

F₁₃ 平均值 1.11×10⁴ 9.91 9.91 5.82×10¹ 6.82 1.78×10² 2.81 4.94×10⁸ 9.91

标准差 1.78×10⁴ 3.37×10^-3 4.57×10^-3 1.66×10¹ 3.15×10^-1 2.80×10¹ 9.85×10^-1 2.34×10⁸ 4.07×10^-3



表 3 100维基准测试函数寻优结果对比 Tab. 3 Comparison of optimization results of 100-dimensional benchmark functions


从表 2可以看出，对于30维单峰基准函数(F₁~F₇)和多峰基准函数(F₈~F₁₃)，在除函数F₆之外的其他函数上，RSSA算法和CSSA算法的平均适应度均小于原SSA算法，其中在函数F₉和F₁₀上收敛到了最小值，其标准差也是远小于SSA算法.这表明两种策略的加入对于提升原始算法的精度是有效的.同时可以看出，联合两种策略的RCSSA算法相对于两种单策略改进算法又有很大程度的提高.除了在函数F₁和F₃上得到了理论最优解，RCSSA算法在其他函数上也获得了比另外两种算法更好的结果.而相对于其他5种优化算法，RCSSA在30维函数上的平均适应度获得了9次领先，其中在函数F₁~F₄和F₉~F₁₁上的优势尤为明显.其余函数结果中，RCSSA在函数F₈和F₁₂上，分别仅次于WOA和PSO算法.

为了进一步测试RCSSA处理高维优化问题的性能，将基准函数F₁~F₁₃的维度扩大至100维，算法参数设置不发生改变，测试结果如表 3所示.随着维度的提高，原SSA算法和其他群优化算法的求解精度越来越差，而RCSSA仍然能保持较高的搜索精度，并且全面超过SSA算法.

函数F₁₄~F₂₃为固定维多峰函数，由于维度较低，因此相对于可变维度的多峰函数来说其局部最优值并不多.这类函数可测试算法在平衡探索和开发能力之间的性能.从表 4可以看到，几种算法在函数F₁₆~F₂₀上的结果相差不大，均能接近理论值，但是在函数F₂₁~F₂₃上，仅有RCSSA算法的结果能够最接近理论值.并且就标准差而言，所提出的算法也在大多数函数中实现了更好的性能.

表 4
表 4 固定维基准测试函数寻优结果对比 Tab. 4 Comparison of optimization results of fixed-dimensional benchmark functions 函数 指标 SSA RSSA CSSA PSO GWO MVO WOA SCA RCSSA

F₁₄ 平均值 1.39 1.73 1.59 3.10 4.69 9.98×10^-1 2.54 1.66 1.53

标准差 8.85×10^-1 9.37×10^-1 1.09 2.40 4.27 2.61×10^-11 2.51 9.51×10^-1 9.64×10^-1

F₁₅ 平均值 3.53×10^-3 4.16×10^-3 5.32×10^-3 5.87×10^-3 8.38×10^-3 6.15×10^-3 7.64×10^-4 1.02×10^-3 2.05×10^-3

标准差 6.72×10^-3 1.22×10^-2 8.47×10^-3 8.25×10^-3 9.95×10^-3 8.72×10^-3 5.35×10^-4 3.90×10^-4 4.99×10^-3

F₁₆ 平均值 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03

标准差 3.83×10^-14 2.21×10^-14 6.60×10^-14 6.52×10^-16 2.52×10^-8 5.48×10^-7 1.11×10^-9 5.59×10^-5 7.92×10^-14

F₁₇ 平均值 3.98×10^-1 3.98×10^-1 3.98×10^-1 3.98×10^-1 3.98×10^-1 3.98×10^-1 3.98×10^-1 4.00×10^-1 3.98×10^-1

标准差 7.36×10^-14 9.11×10^-14 1.32×10^-13 0.00 3.45×10^-6 8.49×10^-7 6.34×10^-6 1.94×10^-3 1.53×10^-13

F₁₈ 平均值 3.00 3.00 3.00 3.00 3.00 3.00 3.00 3.00 3.00

标准差 2.37×10^-13 2.21×10^-13 6.38×10^-13 1.55×10^-15 4.02×10^-5 3.22×10^-6 1.03×10^-4 1.07×10^-4 7.97×10^-13

F₁₉ 平均值 -3.86 -3.86 -3.86 -3.86 -3.86 -3.86 -3.85 -3.86 -3.86

标准差 8.34×10^-11 4.47×10^-11 9.10×10^-12 2.68×10^-15 1.79×10^-3 4.17×10^-6 9.11×10^-3 2.41×10^-3 1.38×10^-11

F₂₀ 平均值 -3.22 -3.23 -3.20 -3.17 -3.26 -3.27 -3.20 -2.89 -3.23

标准差 5.37×10^-2 6.51×10^-2 3.48×10^-2 3.33×10^-1 7.19×10^-2 6.14×10^-2 1.17×10^-1 4.13×10^-1 6.23×10^-2

F₂₁ 平均值 -8.31 -7.22 -5.56 -6.86 -8.80 -7.47 -8.27 -2.76 -1.02×10¹

标准差 2.93 3.30 1.56 3.05 2.28 3.23 2.73 2.07 3.70×10^-11

F₂₂ 平均值 -8.55 -7.61 -5.80 -9.36 -1.01×10¹ -8.25 -7.72 -3.95 -1.04×10¹

标准差 3.16 3.54 1.84 2.41 1.42 3.18 3.41 2.29 5.31×10^-11

F₂₃ 平均值 -8.45 -7.53 -5.85 -9.38 -1.01×10¹ -9.65 -7.11 -3.67 -1.05×10¹

标准差 3.31 3.59 1.87 2.37 1.75 2.35 3.37 1.63 5.17×10^-11



表 4 固定维基准测试函数寻优结果对比 Tab. 4 Comparison of optimization results of fixed-dimensional benchmark functions


3.3.2 收敛性分析图 5给出了各算法在30维基准函数和固定维多峰函数上的寻优收敛曲线，由此可直观地比较9种算法的收敛性能.从图中可以看出，在单峰函数F₁~F₇上，RCSSA算法从迭代初期就保持较高的收敛速度，并且获得了函数F₁和F₃的全局最优.而很明显SSA算法和其他算法在这些函数上陷入了局部最优.多峰函数F₉~F₁₃上，RCSSA在不到10次已经找到全局最优.在固定维函数F₁₄和F₁₆~F₂₀上，几种算法的收敛速度相差不大，但是在F₂₁~F₂₃上，显然RCSSA算法的收敛速度和精度均优于其他算法.这些收敛图像充分表明了RCSSA算法在低维函数上优越的寻优能力.

Fig. 5
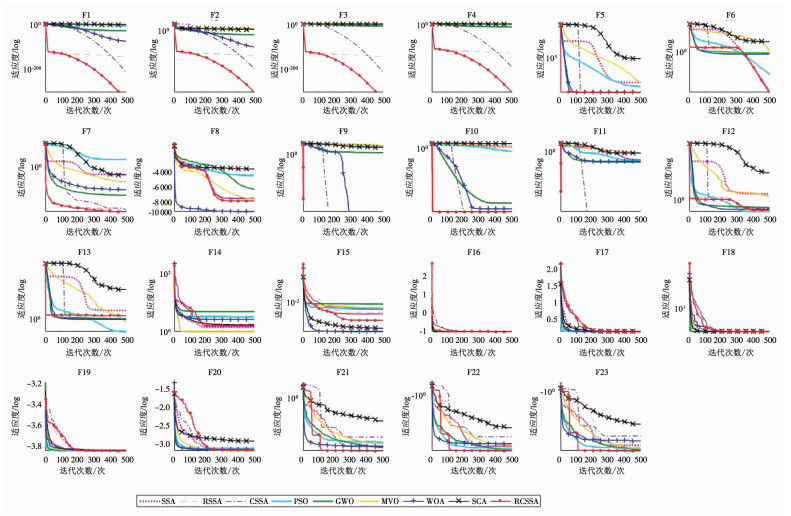图 5 各种算法收敛曲线 Fig. 5 Convergence curves of different algorithms


通过分析表 2~表 4以及图 5，可以得出结论：联合ROBL机制和自适应控制因子的RCSSA算法在总体上优于原SSA算法、两种单策略改进的SSA算法和其他5种优化算法，表现出更高的搜索精度、收敛速度以及稳定性.

3.4 RCSSA求解工程设计优化问题本节从文献[22]中选取圆柱形压力容器设计优化问题以进一步测试RCSSA的性能.如何设计各类尺寸，使得压力容器总成本最小化是该工程优化问题的主要目标，其中成本包括焊接成本、材料和成型.为了解决这个问题，必须确定4个参数的最佳值：顶盖壁厚度T，管壁厚度t，容器管身长度L和内径R，如图 6所示.为了方便，将自变量进行编号，得$\overrightarrow x = \left[ {{x_1}{x_2}{x_3}{x_4}} \right] = \left[ {tTRL} \right]$.问题的目标函数f、约束条件g和各自变量的取值范围如下所示：

Fig. 6
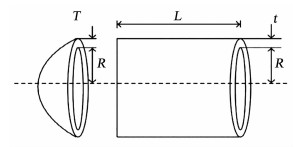图 6 压力容器设计问题 Fig. 6 Pressure vessel design problem


$\begin{array}{l}\overrightarrow {f\left( x \right)} = 0.622\;4{x_1}{x_3}{x_4} + 1.778\;1{x_2}x_3^2 + \\3.166\;1x_1^2{x_4} + 19.84x_1^2{x_3}.\\\left\{ {\begin{array}{*{20}{l}}{{g_1}\overrightarrow {\left( x \right)} = - {x_1} + 0.019\;3{x_3} \le 0, }\\{{g_2}\overrightarrow {\left( x \right)} = - {x_3} + 0.009\;54{x_3} \le 0, }\\{{g_3}\overrightarrow {\left( x \right)} = - {\rm{ \mathsf{ π} }}x_3^2{x_4} - \frac{4}{3}{\rm{ \mathsf{ π} }}x_3^3 + 1\;296\;000 \le 0}\\{{g_4}\overrightarrow {\left( x \right)} = {x_4} - 240 \le 0, }\end{array}} \right.\\0 \le {x_1}, {x_2} \le 99.10 \le {x_3}, {x_4} \le 200.\end{array}$

根据文献[23]，将RCSSA算法的种群规模和最大迭代次数分别设置为20和500，独立运行20次后取最优值.在相同试验条件下，所得结果以及文献中已有的试验结果列于表 5.由表 5可知，RCSSA是处理该问题的最佳优化算法，与其他算法相比可获得更好的结果.进一步说明了RCSSA可应用于实际问题且具有较好的优化效果.

表 5
表 5 各算法的压力容器设计结果对比 Tab. 5 Comparison of optimization results of different algorithms for pressure vessel design 算法 顶盖壁厚T 容器壁厚t 长度L 内半径R 成本

RCSSA 0.780 607 0.385 856 40.445 859 98 198.252 980 5 889.593 30

SSA 0.790 678 0.390 834 40.967 738 75 195.918 220 6 012.188 50

GWO^[5] 0.812 500 0.434 500 42.098 181 00 176.758 730 6 051.563 90

WOA^[6] 0.812 500 0.437 500 42.098 269 90 176.639 000 6 059.741 00

MVO^[20] 0.812 500 0.437 500 42.090 738 20 176.738 690 6 060.806 60

SCA^[21] 0.812 500 0.433 750 42.048 610 00 177.707 800 6 076.365 10

HHO^[23] 0.817 584 0.407 293 42.091 745 76 176.719 640 6 000.462 59

MFO^[24] 0.812 500 0.437 500 42.098 445 00 176.636 596 6 059.714 30

CSS^[25] 0.812 500 0.437 500 42.103 624 00 176.572 656 6 059.088 80



表 5 各算法的压力容器设计结果对比 Tab. 5 Comparison of optimization results of different algorithms for pressure vessel design


4 结论本文基于折射反向学习机制与自适应控制因子提出了一种新型改进SSA算法.首先采用ROBL机制在每一次个体的求解中计算折射反向解，从而能够提高探索和增加原SSA算法的收敛能力.其次将SSA算法中引导者的自适应控制因子引入至跟随者的位置更新中，有效地控制整个搜索过程并增加了算法的局部开发能力.

对23个不同类型与维数的基准测试问题以及一个工程设计优化问题进行了仿真实验研究，详细分析了所提算法的探索、开发和跳出局部最优的能力.其研究结果表明：所提RCSSA算法可以有效提升原SSA算法的优化性能，其在整体性能上要明显优于GWO、WOA、SCA等多个当前最先进的群智能优化算法，并适用于处理高维函数优化问题.RCSSA在对工程设计问题进行优化时，其求解精度、收敛速度也均具有显著的优越性.在未来的研究工作中，RCSSA算法将进一步与工程应用相结合，以期解决更多实际优化问题.


参考文献
[1] EWEES A A, ABD ELAZIZ M, HOUSSEIN E H. Improved grasshopper optimization algorithm using opposition-based learning[J]. Expert Systems with Applications, 2018, 112: 156. DOI:10.1016/j.eswa.2018.06.023


[2] DRAA A, CHETTAH K, TALBI H. A Compound Sinusoidal Differential Evolution algorithm for continuous optimization[J]. Swarm and Evolutionary Computation, 2019, 50: 100450. DOI:10.1016/j.swevo.2018.10.001


[3] KASSARWANI N, OHRI J, SINGH A. Performance analysis of dynamic voltage restorer using improved PSO technique[J]. International Journal of Electronics, 2019, 106(2): 212. DOI:10.1080/00207217.2018.1519859


[4] PAN W T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69. DOI:10.1016/j.knosys.2011.07.001


[5] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46. DOI:10.1016/j.advengsoft.2013.12.007


[6] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51. DOI:10.1016/j.advengsoft.2016.01.008


[7] 滕志军, 吕金玲, 郭力文, 等. 一种基于Tent映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报, 2018, 50(11): 40.
TENG Zhijun, LV Jinling, GUO Liwen, et al. An improved hybrid grey wolf optimization algorithm based on Tent mapping[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 40. DOI:10.11918/j.issn.0367-6234.201806096


[8] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163. DOI:10.1016/j.advengsoft.2017.07.002


[9] 陈涛, 王梦馨, 黄湘松. 基于樽海鞘群算法的无源时差定位[J]. 电子与信息学报, 2018, 40(7): 1591.
CHEN Tao, WANG Mengxin, HUANG Xiangsong. Time difference of arrival passive location based on salp swarm algorithm[J]. Journal of Electronics & Information Technology, 2018, 40(7): 1591. DOI:10.11999/JEIT170979


[10] EL-FERGANY A A. Extracting optimal parameters of PEM fuel cells using salp swarm optimizer[J]. Renewable Energy, 2018, 119: 641. DOI:10.1016/j.renene.2017.12.051


[11] 刘森, 贾志成, 陈雷, 等. 基于樽海鞘群体优化非负矩阵分解的高光谱图像解混算法[J]. 计算机辅助设计与图形学学报, 2019, 31(2): 315.
LIU Sen, JIA Zhicheng, CHEN Lei, et al. Hyperspectral images unmixing based on nonnegative matrix factorization optimized by salp swarm algorithm[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(2): 315. DOI:10.3724/SP.J.1089.2019.17189


[12] SAYED G I, KHORIBA G, HAGGAG M H. A novel chaotic salp swarm algorithm for global optimization and feature selection[J]. Applied Intelligence, 2018, 48: 3462. DOI:10.1007/s10489-018-1158-6


[13] FARIS H, MAFARJA M M, HEIDARI A A, et al. An efficient binary salp swarm algorithm with crossover scheme for feature selection problems[J]. Knowledge-Based Systems, 2018, 154: 43. DOI:10.1016/j.knosys.2018.05.009


[14] ALI IBRAHIM R, EWEES A A, OLIVA D, et al. Improved salp swarm algorithm based on particle swarm optimization for feature selection[J]. Journal of Ambient Intelligence and Humanized Computing, 2019, 10: 3155. DOI:10.1007/s12652-018-1031-9


[15] WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67. DOI:10.1109/4235.585893


[16] TIZHOOSH H R. Opposition-based learning: A new scheme for machine intelligence[C]//Proceedings of International Conference on Computational Intelligence for Modelling Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Vienna, Austria: IEEE, 2005: 695. DOI: 10.1109/CIMCA.2005.1631345


[17] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Quasi-oppositional differential evolution[C]//Proceedings of 2007 IEEE Congress on Evolutionary Computation. Singapore: IEEE, 2007: 2229. DOI: 10.1109/CEC.2007.4424748


[18] 邵鹏, 吴志健, 周炫余, 等. 基于折射原理反向学习模型的改进粒子群算法[J]. 电子学报, 2015, 43(11): 2137.
SHAO Peng, WU Zhijian, ZHOU Xuanyu, et al. Improved particle swarm optimization algorithm based on opposite learning of refraction[J]. Acta Electronica Sinica, 2015, 43(11): 2137. DOI:10.3969/j.issn.0372-2112.2015.11.001


[19] 王光, 金嘉毅. 融合折射原理反向学习的飞蛾扑火算法[J]. 计算机工程与应用, 2019, 55(11): 46.
WANG Guang, JIN Jiayi. Moth-flame optimization algorithm fused on refraction principle and opposite-based learning[J]. Computer Engineering and Applications, 2019, 55(11): 46. DOI:10.3778/j.issn.1002-8331.1809-0091


[20] MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-Verse Optimizer: a nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495. DOI:10.1007/s00521-015-1870-7


[21] MIRJALILI S. SCA: A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120. DOI:10.1016/j.knosys.2015.12.022


[22] SANDGREN E. Nonlinear integer and discrete programming in mechanical design optimization[J]. Journal of Mechanical Design, 1990, 112(2): 223. DOI:10.1115/1.2912596


[23] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization:Algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849. DOI:10.1016/j.future.2019.02.028


[24] MIRJALILI S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228. DOI:10.1016/j.knosys.2015.07.006


[25] KAVEH A, TALATAHARI S. A novel heuristic optimization method: Charged system search[J]. Acta Mechanica, 2010, 213(3/4): 267. DOI:10.1007/s00707-009-0270-4