Author NameAffiliation
Cheng Liu State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, CollaborativeInnovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
Yiding Hu State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, CollaborativeInnovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
Zheng Li State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, CollaborativeInnovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
Decheng Wan State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, CollaborativeInnovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
Abstract:
Breaking wave is a complex physical phenomenon that takes place at the gas-fluid interface, which is the chief reason for the generation of two-phase turbulence, wave energy dissipation, and mass transfer between air and water. For marine hydrodynamics, the breaking bow wave of high speed vessels induces the bubble-mixed flow travelling around the ship, eventually developing to be the turbulent wake which is easy to be detected by photoelectric equipment. Besides, the flow-induced noise stemming from wave plunging may weaken the acoustic stealth of water surface craft. In the oceanographic physics context, wave breaking accounts for the energy and mass exchange of the ocean-atmosphere system, which has a great effect on the weather forecasts and global climate predictions. Due to multi-scale properties of multiphase turbulent flows, a wide range of time and length scales should be resolved, making it rather complicated for experimental and numerical investigations. In early reviews[1-4], general mechanisms related to wave breaking problems are well-described. However, previous emphasis lies on the phenomenological characteristics of breaking wave. Thus, this review summarizes the recent experimental and numerical advances of the studies of air entrainment, bubble distribution, energy dissipation, capillary effect, and so on.
Key words: wave breaking energy dissipation air entrainment and void fraction bubble and droplet size distribution capillary effects
DOI:10.11916/j.issn.1005-9113.19036
Clc Number:O353.2
Fund:
Cheng Liu, Yiding Hu, Zheng Li, Decheng Wan. Review: Recent Advancement of Experimental and Numerical Investigations for Breaking Waves[J]. Journal of Harbin Institute of Technology (New Series), 2019, 26(5): 1-16. DOI: 10.11916/j.issn.1005-9113.19036

Fund Sponsored by the National Natural Science Foundation of China (Grant Nos. 51879159, 51490675, 11432009, and 51579145), the Chang Jiang Scholars Program (Grant No. T2014099), the Shanghai Excellent Academic Leaders Program (Grant No. 17XD1402300), the Program for Professor of Special Appointment (Eastern Scholar) at the Shanghai Institutions of Higher Learning (Grant No. 2013022), and the Innovative Special Project of Numerical Tank of Ministry of Industry and Information Technology of China (2016-23/09) Corresponding author Decheng Wan, Distinguished Professor of Yangtze River Scholar. E-mail: dcwan@sjtu.edu.cn Article history Received: 2019-04-18
Contents Abstract Full text Figures/Tables PDF
Review: Recent Advancement of Experimental and Numerical Investigations for Breaking Waves
Cheng Liu, Yiding Hu, Zheng Li, Decheng Wan


State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
Received: 2019-04-18
Sponsored by the National Natural Science Foundation of China (Grant Nos. 51879159, 51490675, 11432009, and 51579145), the Chang Jiang Scholars Program (Grant No. T2014099), the Shanghai Excellent Academic Leaders Program (Grant No. 17XD1402300), the Program for Professor of Special Appointment (Eastern Scholar) at the Shanghai Institutions of Higher Learning (Grant No. 2013022), and the Innovative Special Project of Numerical Tank of Ministry of Industry and Information Technology of China (2016-23/09)
Prof. Decheng Wan received his Ph.D from Shanghai Jiao Tong University (SJTU), China in 1994. He became a lecturer of Shanghai University in 1994, and was promoted to be an associate professor of Shanghai University in 1996. After successively working as a research fellow of the Royal Society at University College London, UK, a senior research fellow at National University of Singapore, and a Wissenschaftliche Angestellter at Dortmund University, Germany from 1997 to 2005, he returned to Shanghai and was appointed as a full professor of Shanghai Jiao Tong University in 2006. He was selected as a distinguished professor of Shanghai Eastern Scholar in 2008, and promoted as a chair professor of Chang Jiang Scholar of China in 2014, distinguished professor of Shanghai Jiao Tong University in 2015, and Shanghai Excellent Academic Leaders in 2017. Currently, Prof. Wan is Head of Computational Marine Hydrodynamics Laboratory (CMHL, http://dcwan.sjtu.edu.cn/) at SJTU
His research interests include computational marine and coastal hydrodynamics, computational marine hydrodynamics, simulation based design for offshore and polar structures, renewable energy in deep sea, numerical marine basin, nonlinear wave theory, wave loads on structures, numerical analysis of riser vortex-induced vibration (VIV) and platform vortex-induced motion (VIM), fluid-structure interaction, offshore wind turbine and other offshore renewable resources, as well as high performance computation on complex ship and ocean engineering flows, and so on. In these areas, he has published over 480 papers and carried out more than 30 projects on marine hydrodynamics and computational hydrodynamics. He is board of directors and chair of International Hydrodynamic Committee (IHC) of International Society of Offshore and Polar Engineering (ISOPE), member of advisor committee of International Towing Tank Conference (ITTC), member of energy saving method specialist committee and CFD specialist committee of International Towing Tank Conference (ITTC), member of steering committee of CFD Workshops in Ship Hydrodynamics, standing council member of Association of Global Chinese Computational Mechanics, and member of external advisory committee (EAC) of the Department of Ocean Systems Engineering (OSE) of Korea Advanced Institute of Science and Technology (KAIST). He is associate editor of Journal of Hydrodynamics, Journal of Ocean Science and Engineering, as well as member of Editorial Board of Ocean Engineering, Applied Ocean Research, Journal of Ocean and Wind Energy, Journal of Shipping and Ocean Engineering, International Journal of Naval Architecture and Ocean Engineering, Journal of Ship Mechanics, Journal of Marine Science and Applications, Journal of China Ship Research, as well as Journal of Chinese Quarterly of Mechanics.
Corresponding author: Decheng Wan, Distinguished Professor of Yangtze River Scholar. E-mail: dcwan@sjtu.edu.cn.
Abstract: Breaking wave is a complex physical phenomenon that takes place at the gas-fluid interface, which is the chief reason for the generation of two-phase turbulence, wave energy dissipation, and mass transfer between air and water. For marine hydrodynamics, the breaking bow wave of high speed vessels induces the bubble-mixed flow travelling around the ship, eventually developing to be the turbulent wake which is easy to be detected by photoelectric equipment. Besides, the flow-induced noise stemming from wave plunging may weaken the acoustic stealth of water surface craft. In the oceanographic physics context, wave breaking accounts for the energy and mass exchange of the ocean-atmosphere system, which has a great effect on the weather forecasts and global climate predictions. Due to multi-scale properties of multiphase turbulent flows, a wide range of time and length scales should be resolved, making it rather complicated for experimental and numerical investigations. In early reviews[1-4], general mechanisms related to wave breaking problems are well-described. However, previous emphasis lies on the phenomenological characteristics of breaking wave. Thus, this review summarizes the recent experimental and numerical advances of the studies of air entrainment, bubble distribution, energy dissipation, capillary effect, and so on.
Keywords: wave breaking energy dissipation air entrainment and void fraction bubble and droplet size distribution capillary effects
1 Experimental Studies In last few decades, a number of important experiments have been performed and fully analyzed to reveal the intrinsic physics of breaking waves. Different measurement methods including the high-speed cameras, bubble detection approach[5], fiber optical probes[6-7], Laser Doppler Velocimer[8], Particle Image Velocimetry (PIV) technologies[9], and acoustic measurement[10] have been adopted.
By applying a visualization technique, Bonmarin[11] analyzed the steep wave breaking evolution. The wave profile of a plunging crest, the related splash-up, and the air-entrainment phenomenon were observed. Qiao and Duncan[12] performed detailed analysis for the unsteady evolution of moderate spilling wave breakings. Grue and Jensen[13] measured the velocity field and corresponding accelerations of the steep plunging waves from experiment. They found that for the horizontal and vertical accelerations over 1.1g(g indicates the acceleration of gravity) and 1.5g, the wave breaking phenomenon will be induced.
The experiment of breaking waves over an underwater hydrofoil conducted by Duncan[14-15] was the first attempt to study the energy dissipation caused by wave breaking. Rapp and Melville[8] studied the dispersion of the deep-water wave breakings by using Laser Doppler measurement. They measured the loss of excess momentum and energy flux of breaking waves, and found over 10% flux loss for single spilling wave breakers to as much as 25% flux loss for plunging wave breakers. Chang and Liu[16] investigated the turbulent flow originated from wave breaking with limited water depth. By applying the ensemble average approach, the mean velocity, Reynolds stress, and strain rate were obtained. It was concluded that the generation and evolution of turbulence flows including its dissipation are of equal importance, whereas the effect of turbulence diffusion occupies a small portion. Kimmoun and Branger[17] performed the waves breaking test in water tank by using a wedge body. They calculated the spatial derivatives to acquire adequate information for describing the flow structures.
Many existing experimental studies suggest that the air fractions in wave-turbulence interaction process can induce low-frequency-noise in the ocean. For a better understanding of the air entrainment caused by wave breaking, Lamarre and Melville[18] exploited the bubble plumes and found that the magnitude of containing air fractions is many orders larger than previous expectation. It was concluded that the contribution of bubbles to sound propagation might be underestimated to a very large extent if these plumes of large bubbles are out of consideration. Later on, Lamarre and Melville[19]gave detailed measurements for the evolution of the void-fraction field in bubble plumes originated from large-scale deep water breakers. Various parameters of air fractions were calculated and comparison was made with previous 2-D laboratory breaking waves. In the experiment performed by Cartmill and Su[20], bubble radii in the bounds of 34 to 1 200 μm were measured by an acoustic sensor at different locations and deepness in a water tank, and the scatters of bubble size are well conformed with -3 power-law from 10 to 1 200 μm. Loewen et al.[10]applied an image processing technology to measure the size scatters of large bubbles generated by breaking waves in fresh and salt water. They found that the distributions of bubble size can be described by an exponential (or power law) equation, and concluded that the gas transportation resulted from large bubbles should be taken into consideration even for the low-speed wind. By measuring the bubble dimensions for breaking waves in open water and laboratory experiment, Deane and Stokes[5] gave a quantitative illustration of the bubble generation principles. They found that for bubbles dimensions greater than about 1 mm, the bubble density conforms a -10/3 power law correspondent to the bubble radius, in which the bubble size distribution is dominated by turbulence intensity. In terms of smaller bubbles stemming from droplet and jet impact, a -3/2 power-law can be deduced. Air entrainment of typical gravity wave breakers on a slope-beach was studied experimentally by Mori and Kakuno[21], in which the wave surface altitude, air fractions, and bubble transportation were analyzed in detail. Experimental results revealed a linear dependence between the air portions and turbulent intensity. Besides, the bubble distributions were observed to follow a -3.4 power law against the bubble diameters. It was noted that the bubble transportation has no significant relations with the breaking positions and free surface depth. Based on the experiment of Blenkinsopp and Chaplin[22], further measurements were performed in the water tank to study the transportation of void fractions originated from the wave breaking of fresh water, salted water, and sea water. Experimental results suggested that the influence of water type might be less significant compared with the scale effect for investigating the evolution of bubble plumes entrained due to breaking waves.
Andreas[23] was the first to analyze the transportation of seawater spray. In the study, previous droplets creation functions were summarized, and new formula for wind speeds over 32 ms-1 were proposed. The droplet size distribution under strong wind conditions were also studied experimentally by Veron et al.[24] by using high speed video camera. It showed that the droplet dimension distribution follows -3 to -5 power laws when the droplets diameters vary between 196 and 5 510 mm. The creation of droplets by two kinds of plunging waves was studied systematically by Towle[25], and results revealed that the wave breakers induced by larger wave steepness generally lead to larger numbers of droplets with greater radius.
By using high-image-density PIV, Lin and Rockwell[9] studied the evolution of quasi-steady breaker in different stages, including the capillary wave pattern and the fully developed breaking waves. For high Froude number, surface tension plays an important role to determine the breaker characteristics. In terms of intermediate Froude numbers, the evolution of free surface exhibits capillary wave pattern. Quasi-steady breaking waves accompany with flow separation may be generated by high Froude number at the breaker zone.
Some of the representative experimental investigations for breaking waves are summarized in Table 1.
表 1
Duncan[14-15] 1981
1983 Camera Breaking waves due to submerged hydrofoil Surface profile, dimensions of turbulent wake
Bonmarin[11] 1989 Camera Deep water wave breaking Splash phenomenon, air entrainment
Rapp and Melville[8] 1990 LDV Deep water wave breaking Kinetic energy loss, air entrainment and dissipation
Lamarre and Melville[18-19] 1991
1994 Acoustic instruments, camera Deep water breaking waves Contribution of bubbles to sound propagation
Cartmill and Su[20] 1993 Acoustic instruments Deep water breaking waves Bubble size distribution
Lin and Rockwell[9] 1995 PIV, camera Quasi-steady breaking wave Surface tension effect
Loewen et al.[10] 1996 Acoustic instruments, camera Breaking waves in freshwater and saltwater Bubble size distribution
Chang and Liu[16] 1999 Camera Breaking waves of intermediate depth Turbulence production, dissipation
Qiao and Duncan[12] 2001 PIV, Camera Spilling breakers Surface tension effect
Deane and Stokes[5] 2002 Bubble interface detection Breaking waves in laboratory and open ocean Bubble density, size distributions
Grue and Jensen[13] 2006 PIV Deep water plunging breaking Overturning jet and wave induced acceleration
Rojas and Loewen[6] 2007 Fiber optical probes, camera Deep water breaking waves Peak, mean void fractions
Kimmoun and Branger[17] 2007 PIV Sloping beach wave breaking Full velocity field, void fraction of the surf zone.
Blenkinsopp and Chaplin[22] 2007 Fiber optical probes, camera Breaking waves in fresh water, salted water and sea water Distribution of void fractions, effect of scale
Mori and Kakuno[21] 2008 Camera Wave breaking in sloping beach Free surface elevation, void fraction, bubble distribution, turbulent intensity
Blenkinsopp and Chaplin[7] 2010 Fiber optical probes, camera Breaking waves induced by submerged reef Spatial, temporal evolution of the bubble plumes
Veron et al.[24] 2012 Camera Breaking waves under strong wind Droplet size distribution under strong wind conditions
Towle[25] 2014 Camera Plunging breaking waves Amounts, droplets size distribution
Table 1 Experimental and open ocean investigations for breaking waves
2 Numerical Studies Experimental research can only be done for usual wave conditions due to technical difficulties. Thus, it is difficult to acquire an intensive understanding of the multi-scale wave breaking phenomenon. Due to the existence of complex hydrodynamic characteristics(e.g., complex breaking patterns, coalescence and separation of bubbles/droplets, and multiscale liquid-gas turbulence), simulating the surf zone breaking waves is still a challenge for traditional CFD. With recent progresses of the numerical approaches, it becomes feasible to resolve the two-phase flow problems numerically even with the presence of the above difficulties. Because of the recent advances in computer architecture, detailed numerical studies of the intermediate scale wave breaking problems that takes account of water droplets and air bubbles become possible. Scardovelli and Zaleski[26] provided a well-documented review on different numerical approaches.
In early numerical studies, Lemoes[27]; Takikawa et al.[28]; Lin and Liu[29-30]; Bradford[31] adopted the Reynolds Averaged Navier-Stokes (RANS) models for the analysis of breaking waves. Although the understanding of the fundamental wave breaking phenomenon arising in the surf zone can be improved accordingly, the turbulent intensity was over predicted at the breaking regions. Hieu et al.[32] and Zhao et al.[33] developed multi-scale method that can improve original RANS predictions. The 2-D flow structures can be fully resolved by RANS model, while the 3-D turbulence interactions are represented by the specified eddy viscosity model. Although air entrainment was not involved, the numerical results are generally consistent with experimental data.
Large eddy simulations (LES) and direct numerical simulations (DNS) are two major branches for the high-fidelity simulation of the turbulent wave breaking. In LES, the large scales eddies are modeled directly, while sub-grid viscosity model and bubbly-flow models are utilized for representing small scale eddy. Thus, Navier-Stokes equations can be solved using the computational mesh with moderate refinement. Shi et al.[34], Liang et al.[35-36], and Derakhti and Kirby[37] developed turbulent bubbly flow models for the closure of governing equations. The numerical work of Zhao and Tanimoto[38] was the first attempt to simulate breaking waves of a two-dimensional configuration by using LES method, in which good agreement was obtained compared with experimental measurements. Watanabe and Saeki[39] presented the first numerical results of 3-D LES of a plunging breaking wave. Similar 3-D numerical experiment of plunging breakers were conducted by Mutsuda and Yasuda[40], in which air entrainment and bubble interactions were discussed in detail. Christensen and Deigaard[41] studied spilling breaking wave and plunging breaking wave with different intensity. Phenomenology study with a visualization of the internal velocity field were given. 3-D vortex structures created by the wave breaker in surf zone were investigated by Watanabe et al.[42] with the adoption of single-phase model.
In contrast, as a promising technology, DNS is becoming prevalent in solving the multi-phase flow since no parametrizations are required. It is noted that the mesh resolution should be sufficiently refined to be taken into account of the small-scale flow structures. The early-stage numerical models by Lin and Liu[29-30] as well as Bradford[31] failed in considering air entrainment details until the studies of Lubin et al.[43] and Biausser et al.[44] DNS are often adopted to study the evolution of wave breakings to provide numerical data on wave dissipation and the splashing processes. Periodic wave conditions with relatively small wavelengths are usually adopted, and representative research works can be found in Refs.[45-49]. The physical processes of wave breaking, velocity profiles, and breaking intensities for plunging breakers were investigated by Chen et al.[45] Iafrati[50-51] provided quantitative statistics of the spray and air fraction in breaking waves. Numerical investigation of plunging breaking wave past an underwater bump were performed by Kang et al.[52] and Koo et al.[53], in which the whole plunging wave breaking procedure including the jet diving and secondary jet were analyzed.
Considering the computational cost for the 3-D cases, the simulations mentioned above were mainly conducted in 2-D domain. In addition, most of the DNS studies aimed at low-Reynolds-number problems. However, since 2-D simulations cannot capture the flow structure of Langmuir revolution in wave breaking proceedings[54], 3-D simulations are necessary to fundamentally investigate the 3-D phenomenon including bubble and spray formation. The differences between 2-D and 3-D results were compared by Lubin et al.[43], and numerical simulation revealed that the energy dissipation after the wave breaking can be enhanced by 3-D turbulent flow, while the enhancement is less than 5% for half-wave period. To alleviate such computational burdens of 3-D simulations, Sullivan et al.[55-56] developed an approach with intermediate complexity. Different from the complete model of the breaking waves, a stochastic term was added in momentum equation with a linearizing free-surface condition to represent the existence of wave breaking. This model has been used to study the wave breaking phenomenon considering Langmuir circulation. However, forcing terms should be defined to keep consistence with the experimental measurements. Thus the stochastic model cannot capture the air entrainment, and the density changes and buoyancy effect are not involved in current stage (Sullivan et al.[56]).
Recently, with the rapid development of numerical schemes and computer hardware, more investigations have been conducted to 3-D DNS focusing on the vortex structures, energy dissipation, and air entrainment, represented research works were given by Christensen[57]; Fuster et al.[58]; Brucker et al.[59]; Lakehal and Liovic[60]; Zhou et al.[61]; Lubin and Glockner[62], etc.
In the study of Brucker et al.[59], up to 134 million grids were used and numerical tests showed that the parallel scalability remain acceptable. More recent numerical study presented by Lubin and Glockner[62] used over 1 billion grids to investigate the vortex filaments created at an early stage after the occurrence of breaking. In the studies of Stern et al.[63] and Wang et al.[64], bow wave breakings adjacent to the wedge shape obstacle and breaking wave past a underwater bump were simulated using very large grids (up to 2.2 billion), which was the first endeavor to simulate wave-breaking problems with the mesh resolution scale around micrometers. Table 2 outlines the existing simulation approaches for the fundamental analysis of breaking waves.
表 2
Takikawa[28] 1997 RANS FD 2 Breaking wave transformation system on a slope
Lin and Liu[29-30] 1998 RANS FD 2 Evolution of wave sequence, wave breaking in the slope beach region
Watanabe and Saeki[39] 1999 LES FD 3 Vorticity and velocity field during the wave breaking process
Chen et al.[45] 1999 DNS FD 2 Splash-up phenomenon of plunging breakers
Bradford[31] 2000 RANS FD 2 Spilling and plunging breaking waves past a sloping region
Song, Sirviente[46] 2004 DNS FD 2 Viscous and capillary effects in breaking wave
Sullivan et al.[55] 2004 DNS FD 3 Stochastic model and its application in breaking waves simulation
Hieu et al.[32] 2004 RANS CIP, FD 2 Wave propagation in shallow water (wave shoaling, wave reflection and air movement)
Zhao et al.[33] 2004 RANS FD 2 Multi-scale turbulence model for breaking wave
Watanabe et al.[42] 2005 LES - 3 Wave breaking and the breaking-induced turbulent two-phase flow
Lubin et al.[65] 2006 LES - 3 Overturning, splash-up and air entrainment of plunging breaking processes
Christensen[57] 2006 LES FV 3 Undertow, turbulence in breaking waves
Fuster et al.[58] 2009 DNS FV 3 Atomization of a liquid sheet, capillary effect
Iafrati[49] 2009 DNS - 2 Breaking waves of different initial steepness
Brucker et al.[59] 2010 DNS FD 3 Four types of deep-water breaking waves (weak, strong, and very strong plunging)
Shi et al.[34] 2010 LES FD 2 Air fraction evolution predicted by two-phase flow model
Iafrati[48] 2011 DNS - 2 Energy dissipation in early stage breaking
Lakehal and Liovic[60] 2011 DNS FV 3 Breaking of steep water waves on a beach of constant bed slope
Liang et al.[36] 2012 LES - 2 Multi-size multi-gas bubble model to study evolution of bubbles
Kang et al.[52], Koo et al.[53] 2012 DNS - 2 Plunging breakers for wave past a submerged bump
Wang et al.[64] 2016 DNS FD 3 Small-scale two-phase flow structures in a breaking wave
Derakhti and Kirby[37] 2014 LES - 3 LES model to incorporate entrained bubble populations
Zhou et al.[61] 2014 LES FV 3 Wave breaking-induced turbulence on seabed
Lubin and Glockner[62] 2015 DNS FD 3 Visualization of vortex filaments and its evolution for plunging breaking waves
Deike et al.[49] 2015 DNS FV 3 Void fraction, bubble distribution, energy dissipation, surface tension effect
*FD: finite difference; FV: finite volume; CIP: constraint interpolation profile.
Table 2 Numerical investigations for breaking waves
3 Mechanism Analysis The breaking process of complex multiphase turbulent flows is a challenging problem for analysis. General conclusions of the unsteady and statistical characteristics of the energy dissipation, air entrainment, bubble cloud, aerated vortex filaments, and the capillary effect are summarized and presented in this section. Corresponding statistical methodologies and important conclusions are also introduced and discussed.
The typical breaking procedure can be described in following aspects. As shown in Figs. 1(a)-(c) (reproduced from Wang et al.[64]), a jet was first formed in the wave forward direction (Fig. 1(a)), and then it impacted the water surface due to gravity (Fig. 1(b)). In the initial breaking stage, the wave dynamics exhibited 2-D flow pattern. Afterwards, the jet impacting and entrapment of air cavity brought numerous bubbles and droplets, and the flow became fully three dimensional (Fig. 1(c)). As summarized by Deane and Stokes[5] as well as Kiger and Duncan[66], there are two major reasons for the generation of bubble clouds, i.e., jet impacting the free surface creates small scale bubbles, while the air-bubble collapsing accounts for the formulation of larger bubbles. The influence of initial slope for waves (S) was analyzed numerically by Deike et al.[67], and they found that the wave evolution was close to the plunging breaking with initial slope S>0.42, while a spilling process was observed for 0.35 < S < 0.42, which was also conformed with the experiment done by Rojas and Loewen[68].
Fig.1
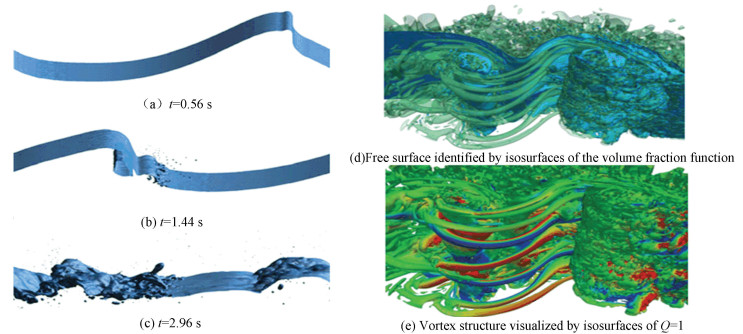 Fig.1 Time evolution of breaking waves (a)-(c) and flow structures(d)-(e), where (a)-(c) are reproduced from Wang et al.[64], (d)-(e) are reproduced from Lubin and Glockner[62].
Fig.1 Time evolution of breaking waves (a)-(c) and flow structures(d)-(e), where (a)-(c) are reproduced from Wang et al.[64], (d)-(e) are reproduced from Lubin and Glockner[62]. In Fig. 1, Figs. 1(d)-(e) show the bottom view of the free surface for breaking waves, in which the air entrainment and cavity break-up process can be demonstrated clearly. The wave impact that induces large air cavity is accompanied by many small-size satellite bubbles. The thin filaments of air, which is an evident phenomenon in wave breaking, are under numerical investigation by Lubin and Glockner[62].
3.1 Energy Dissipation The total energy E=Ek+Eg+Es for wave breaking can be decomposed into three components (the kinetic energy Ek, the gravitational potential energy Eg, and the capillary potential energy Es), according to the formulations given by Chen et al.[45], Iafrati[51], and Deike et al.[49] as follows:
${E_k} = \frac{1}{2}\int \rho {u^2}{\rm{d}}x{\rm{d}}y$ (1)
${E_g} = \int \rho gy{\rm{d}}x{\rm{d}}y$ (2)
${E_s} = \frac{{\gamma (\mathfrak{L} - 1)}}{{{\rho _w}g{\lambda ^2}}}$ (3)
where
Fig. 2(a) shows the time evolution of wave energy, in which ▽ denotes the gravitational potential energy, ◇ represents the capillary potential energy, ○ indicates the kinetic energy, and □ denotes the total energy. Fig. 2(b) shows the wave breaking factors as a function of wave steepness, in which the semi-empirical results are represented by solid line, ▼ indicates the DNS by Deike et al.[67], and other symbols are from the experimental measurements of Banner and Peirson[69], Drazen et al.[70] and Grare et al.[71] Fig. 2(c) shows the total wave energy, kinetic energy, and gravitational potential energy as a function of time.
Fig.2
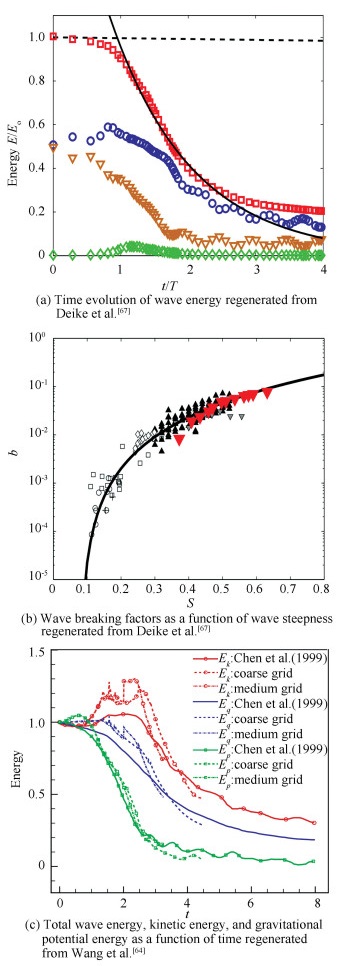 Fig.2 Numerically predicted energy dissipation as a function of time
Fig.2 Numerically predicted energy dissipation as a function of time Followed the theoretical study of Phillips[72], the energy dissipation rate caused by breaking waves can be described by
${E_k} = b = 0.4{(S - 0.08)^{2.5}}$ (4)
where S=0.08 is an estimation of the threshold for breaking. The accuracy of the above inertial model was validated by numerous experimental studies (Deike et al.[49], Romero et al.[76], Garrett et al.[77], Melville and Pizzo[78], and Melville and Fedorov[79]).
Deike et al.[49] compared the evolution of the whole wave energy and the kinetic and gravitational energy per unit length of breaking wave, as shown in Figs. 2(a)-(b). The total wave energy shows an abrupt decrease during the first wave period, which means the majority of the wave energy is dissipated. They also provided a fitted exponential function to predict energy decay which is written as E=E0e-ζt, where ζ represents the decay rate and E0 stands for the primary wave energy per unit width of the wave crest. The breaking influencing factor b against the wave slope is shown in Fig. 2(b), in which the experimental data of Romero et al.[76], Garrett et al.[77], and Drazen et al.[70] together with the 3-D DNS solutions (Deike et al.[49]) were given. Deike et al.[67] inferred that the initial setups for breaking cause the differences in dissipation rate between DNS and experimental result for S varying from 0.35 to 0.4. The kinetic, gravity, and potential energy components derived from 3-D NDS were also given by Wang et al.[64], together with the 2-D DNS solutions by Chen et al.[45] as shown in Fig. 2(c). Although the time evolution of energy exhibits similar trends for 2-D and 3-D simulations in general, a higher jump after jet plunges was observed for 3-D case, which is consistent with the numerical predictions by Lubin et al.[43] and Lubin and Glockner[62].
Deike et al.[49] analyzed components of the breaking waves energy for various factors
Fig.3
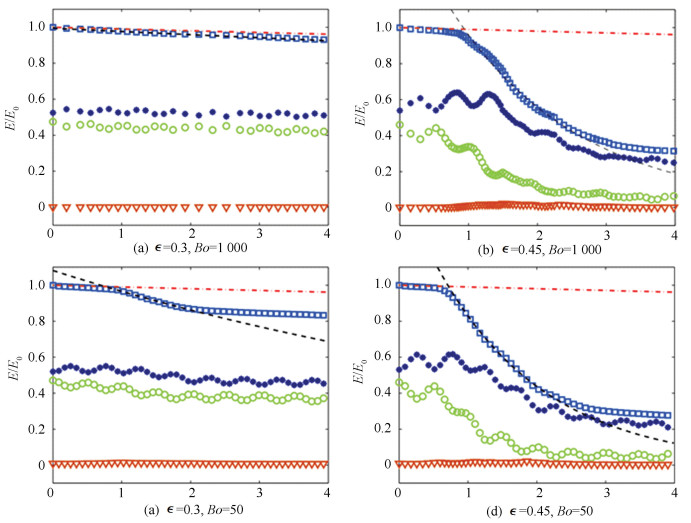 Kinetic energy; Surface tension potential energy: ▽; Gravitational potential energy: ○; Total energy: □Fig.3 Wave energy components as functions of time ((a)-(d) are reproduced from Deike et al.[49])
Kinetic energy; Surface tension potential energy: ▽; Gravitational potential energy: ○; Total energy: □Fig.3 Wave energy components as functions of time ((a)-(d) are reproduced from Deike et al.[49]) When the surface tension effect becomes dominated (Bo=50, 100), it was concluded in Ref. [49] that if the Bond number is relatively low, more energy will be dissipated for non-breaking waves, while the total energy dissipation shows less relevance to the Bond number for the case of breaking wave.
The total energy dissipation affected by initial steepness at different Bond numbers was also provided in Ref.[49]. For low surface tension, the energy dissipation will be promoted for wave steepness larger than the threshold. In terms of strong surface tension, the existence of capillary effect will enhance the energy dissipation rate. It was observed that a larger initial steepness will further increase the total energy dissipation.
3.2 Air Entrainment and Void Fraction Air entrainment occurs when the jet re-contacts the free surface with a large air pocket and bubbles entrained. It also occurs when the droplets drop into the water with high-speed, which was reviewed by Kiger and Duncan[66]. However, the investigation for entrained air was not adequate in their study, so the available corresponding studies were performed by Deane and Stokes[5], Lamarre and Melville[18], and Blenkinsopp and Chaplin[22].
The void fraction has been experimentally studied by repeating measurements at various locations by measuring electric conductivity[19] and using optical fiber probes[6, 22]. Deike et al.[49] obtained void fraction variation through 3-D DNS, in which the predicted bubble flume evolution and the dynamics of void fraction are consistent with the available experimental measurements by Lamarre and Melville[19] and Blenkinsopp and Chaplin[22]. Both plunging case (S=0.55) and spilling breakers (S=0.43) were compared, and in the spilling case, bubble clouds generated by entrained air are accumulated adjacent to the free surface. In terms of plunging breaking waves, larger bubbles rise above the water surface into the air, while small bubbles remain in water phase for longer.
The entrained air evolving with time is presented in Fig. 4(a), which was reproduced from Deike et al.[49] At t/T≈1, the first peak is observed since the jet impacts surface and a big pocket of air is entrapped. Then the measured air volume decreases quickly due to the collapse of the bubble and its re-contact into the free surface. After that, bubbles are created and a secondary air volume peak will be observed, which corresponds to the situation where large amount of bubbles are trapped beneath the water surface. Lamarre and Melville[18] described the fast decay as an exponential function, V=V0e-Kt/T, Deike et al.[67] deduced that the K factor varies from 2.5 to 4, and approximately, it relies on the initial wave steepness. K=3.9 and K=5 were deduced respectively by Lamarre and Melville[19] and Blenkinsopp and Chaplin[22] in their experiments.
Fig.4
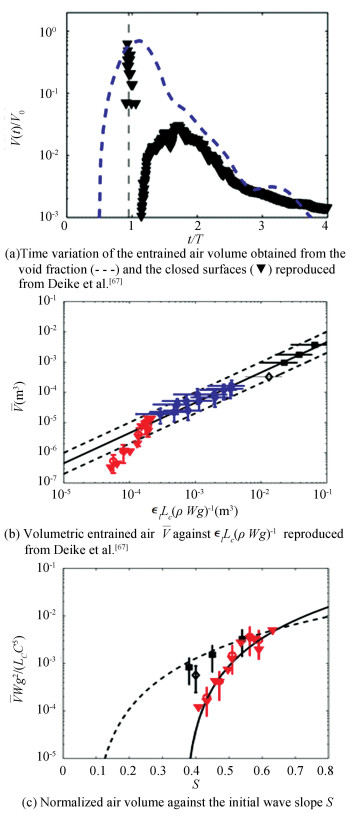 ▼ shows the total volume of air during the active breaking process; ◇represents the experimental results of Deane and Stokes[5]; ■represents the experimental measurement of Lamarre and Melville[19]; ◆represents the experimental results of Duncan[14]Fig.4 Numerically predicted air volume as a function of time
▼ shows the total volume of air during the active breaking process; ◇represents the experimental results of Deane and Stokes[5]; ■represents the experimental measurement of Lamarre and Melville[19]; ◆represents the experimental results of Duncan[14]Fig.4 Numerically predicted air volume as a function of time Deike et al.[67] further deduced the formulation for predicting the time-averaged air entrainment volume against the dissipation rate per unit width of wave crest or the slope, given as, V=Bl
$\bar V = 0.4B{(S - 0.08)^{2.5}}{L_c}{c^5}/W{g^2}$ (5)
Fig. 4(b) shows the total air volume V against
3.3 Bubble and Droplet Size Distribution The identification of the droplets and bubbles was implemented with a neighbor searching algorithm utilizing a non-recursive strategy. Herrmann[80] proposed an efficient identification approach for classifying droplets or bubbles shared by different blocks[49, 67].
Previous experimental investigation by Deane and Stokes[5] indicated that the size distribution of bubbles is dependent with different power law scaling. A theoretical scaling equation accounting for the turbulent fragmentation was proposed by Garrett et al.[77], which is written as
$N(r) \propto Q{\mathit{\boldsymbol{\epsilon}}^{ - \frac{1}{3}}}{r^{ - \frac{{10}}{3}}}$ (6)
where N(r) stands for the bubble numbers in a unit mm, Q and
$N(r) \propto Q{(\sigma /\rho )^{ - \frac{3}{2}}}{v^2}{r^{ - \frac{3}{2}}}$ (7)
where v indicates the jet falling speed. Soloviev and Lukas[81] derived a scaling equation for bubble size distribution based on the analysis of buoyancy forces dominated bubble fraction. Figs. 5(a)-(c) illustrate that bubbles created at the early stages of breaking waves are relatively small while larger bubbles are formed in the later stages of after breaking. Figs. 5(a)-(b) present the bubble size distributions for fine-grid simulations[64], in which the bubble numbers (time-averaged) is close to the experimental measurements (Deane and Stokes[5], Mori and Kakuno[21], and Tavakolinejad[82]). In the simulation work of Wang et al.[64], the two-phase flow is not as violent as those in the experiments, so the slopes are slightly lower than the theoretical and experimental results for large bubbles.
Fig.5
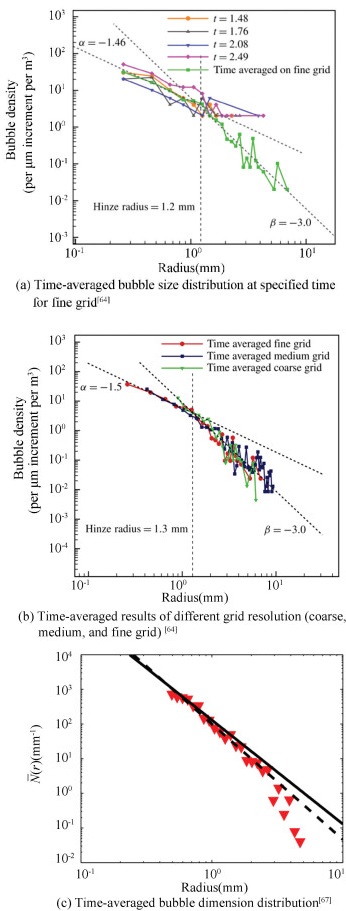 Fig.5 Numerically predicted bubble size distribution
Fig.5 Numerically predicted bubble size distribution In terms of droplet size distribution, a similar scaling equation was given by Garrett et al.[77] and Deane and Stokes[5], which is written as
$N(r) \propto {v^{ - 1}}{(\sigma /\rho )^{\frac{1}{2}}}{r^{ - \frac{9}{2}}}$ (8)
where v represents the jet velocity of the spray. Fig. 6 shows the theoretical and experimental results (Lhuissier and Villermaux[83], Veron et al.[24], and Towle[24]), as well as the numerical predictions of Wang et al.[64]for time-averaged droplet size distribution. It is noted that there are significant differences between the experimental studies and simulations for analyzing the spray formation mechanisms, (e.g., the plunging wave breaking[26]), the high wind speed generated spray spume drops (Veron et al.[24]), and bubble bursting (Lhuissier and Villermaux[83]), however, the distribution of drop size also conforms a scaling power-law. Based on the DNS results of Deike et al.[49], the time-averaged bubble size distribution N(r) against the wave breaking time is presented in Fig. 6, in which N(r) is found to obey a power law with
Fig.6
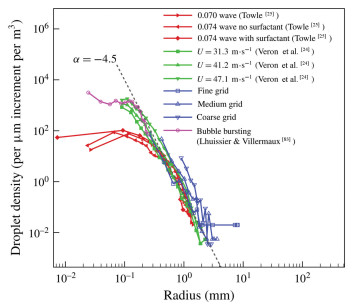 Fig.6 Drop density distribution as a function of radius, which is regenerated from Wang et al.[64]
Fig.6 Drop density distribution as a function of radius, which is regenerated from Wang et al.[64] 3.4 Capillary Effects Few researchers have paid attention to the micro-mechanism inside the wave breaking processes, considering the influence of capillary effects. The surface tension effects were firstly studied by the experiments of Liu and Duncan[85-87]. They found that the breaking kinematic energy dissipation is able to be modified through adding surfactants. Capillary effects on the wave breaking measured in experiment were discussed extensively by Duncan[87]. The numerical investigation of capillary effects was accomplished in the studies of Liu and Duncan[86] and Deike et al.[49]
Deike et al.[49] classified various small-scale wave patterns into four groups, including the gravity induced parasitic capillary waves, non-breaking waves, and spilling and plunging breaking waves. By changing the initial steepness of the wave and the Bond number, a wave-state diagram was summarized, as shown in Fig. 7(a), where PB indicates plunging breakers, SB represents spilling breakers, PCW represents parasitic capillary waves, and NB stands for non-breaking gravity waves. From Fig. 7(b), the critical steepness
Fig.7
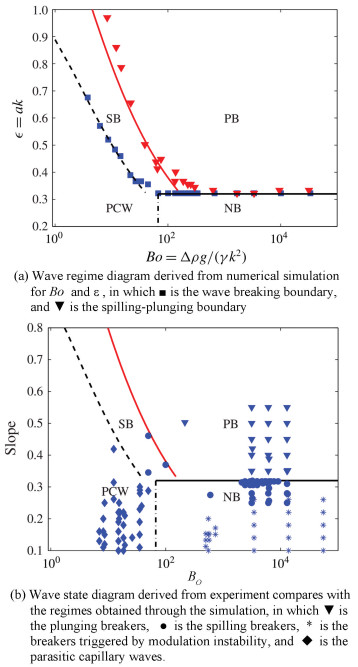 Fig.7 Numerically predicted wave regime diagram
Fig.7 Numerically predicted wave regime diagram As shown in Fig. 7, when surface tension becomes dominated, two types of wave breaking will be induced, i.e., the gravity-capillary breakers and the spilling breakers, and both are scaled as
3.5 Other Research Findings Related to Wave Breaking Recent progress in computational capabilities offers the possibility to study multiscale phenomenon existing in wave breaking. In this subsection, recent development in the simulation of vortex filaments, modulational instability, and wind turbulence over breaking waves are introduced briefly.
The vortex filaments generated in the primary stage of the wave breaking are often observed in laboratories or open sea. Lubin and Glockner[62] confirmed the existence of the unusual vorticial structures under breaking waves and investigated the mechanisms through 3-D DNS. From numerical results, the streamwise vortex filaments were detected with an upstream obliqueness (approximately 50°) under plunging breaking waves. However, Lubin and Glockner[62]pointed out that there is no contribution on the dissipation process due to the presence of the vortex filaments. The formation of large-scale vortex structures in the air induced by the plunging wave and its influence to the interaction between the ocean and atmosphere were investigated numerically by Iafrati et al.[90] The energy dissipated by the wave breaker both in fluid and gas was considered. It is particularly important to note that the energy dissipation in air is larger than that in water. Recently, the wind turbulence over breaking waves was analyzed by Yang et al.[91] in detail. Effects of wave age and wave steepness were investigated through statistics of turbulent airflow over breaking waves.
4 Conclusions and Future Prospect In this review, previous studies for wave breaking phenomenon by laboratory experiments, numerical simulations, and semi-empirical models are summarized. The methodologies for analyzing characteristic variables during wave breaking, including the void fraction, the bubble size distribution, the energy dissipation of the breaking wave, and the time evolution of the total volume of air are illustrated.
In the last few decades, numerous experimental, theoretical, and numerical methods have been proposed for analyzing the breaking waves and their effects in different scales. For experimental and open ocean investigation, extensive measurements for the bubble density, size distribution (Lamarre and Melville[18]; Cartmill and Su[20]; Lin and Rockwell[9]; Deane and Stokes[5]; Mori and Kakuno[21]; Blenkinsopp and Chaplin[7]) under various initial wave steepness were performed. Acoustic resonator, fiber optical probes, and high speed camera were often used for those analyses. Two experiments (Lin and Rockwell[9]; Qiao and Duncan[12]) were designed aiming at analyzing the surface tension effects, in which the PIV technology was adopted for visualizing the velocity field of spilling breakers. Kinetic energy dissipation and turbulence intensity during the breaking procedure were well studied by Rapp and Melville[8], Chang and Liu[16], and Mori and Kakuno[21] with PIV and high speed camera. There were also quantitative statistics for droplets distribution (Veron et al.[24]; Towle[25]) and air entrainment (Bonmarin[11]; Rapp and Melville[8]) during the violent breaking. Compared with experiment, numerical simulations gave more details and deep insights into the complex two-phase flow phenomenon. Among the prevalent numerical methods mentioned in this review, it was noticed that the RANS simulations (e.g., Takikawa et al.[28]; Lin and Liu[29-30]; Bradford[31]) were only conducted in early years. Recently, the LES (e.g., Watanabe et al.[42]; Lubin et al.[62]; Shi et al.[34]), especially the DNS (e.g., Lakehal and Liovic[60]; Wang et al.[64]; Lubin and Glockner[62]; Deike et al.[49]) were more preferred in the fundamental study of wave breaking problems. The statistic of air entrainment (Lubin et al.[43]) and droplet/bubble distribution (Wang et al.[64]), as well as energy dissipation (Deike et al.[49]) were more simple and straightforward from a volume of fluid (VOF) field than from experimental photograph. In terms of semi-empirical method, Romero et al.[76]proposed breaking parameter model, which can be used for estimating dissipation rate. Deike et al.[67] deduced the formulation for predicting the volume of entrained air. Garrett et al.[77] developed bubble size scaling equation accounting for the turbulent fragmentation. Deane and Stokes[5] further provided a scaling equation of small bubbles and droplet size distribution.
Although existing theoretical, experimental, and numerical tools are capable to provide majority characteristics, such as the mean void fraction, and droplet/bubble distribution, many fundamental physical processes of breaking wave are lack of quantitative analysis. For experimental studies, tracking and recording evolution of single droplet/bubble are challenging, especially for fully 3-D experiment. In addition to the reliable approaches for accurate statistics of air entrainment, droplets distributions need further development, and existing PIV technologies cannot provide adequate details for intensive investigations of the turbulent two-phase flows, while the promising X-ray micro-computed tomography technology[92] is considered to be extended for this purpose. For numerical approaches, DNS provides an important alternative in resolving wave breaking mechanism in micro-scale. Due to the high requirement of the computing resources in DNS, adaptive mesh (Liu and Hu[93-96]), which is capable to resolve the minimum bubble/droplet by localized mesh refinement, shows obvious advantage in large scale parallel computation. Besides, the fast algorithm for two-phase flow problems, which can greatly improve the computational efficiency, can be considered in future work. In terms of theoretical methods, up to now, all the semi-empirical formulae mentioned in this review were validated by model experiment and numerical simulations, while the scaling effect is rarely considered. In the future, more experimental and numerical investigations are required to bridge the gap between model scale analysis and real scale applications.
References
[1] Peregrine D H. Breaking waves on beaches. Annual Review of Fluid Mechanics, 1983, 15(15): 149-178. DOI:10.1146/annurev.fl.15.010183.001053 (
 0)
0)[2] Battjes J A. Surf-zone dynamics. Annual Review of Fluid Mechanics, 1988, 20(1): 257-293. DOI:10.1146/annurev.fl.20.010188.001353 (
 0)
0)[3] Svendsen I A, Putrevu U. Surf-zone hydrodynamics. Advances in Coastal and Ocean Engineering, 1996. DOI:10.1142/9789812797575_0001 (
 0)
0)[4] Christensen E D, Walstra D J, Emerat N. Vertical variation of the flow across the surf zone. Coastal Engineering, 2002, 45(3): 169-198. DOI:10.1016/S0378-3839(02)00033-9 (
 0)
0)[5] Deane G B, Stokes M D. Scale dependence of bubble creation mechanisms in breaking waves. Nature (London), 2002, 418(6900): 839-844. DOI:10.1038/nature00967 (
 0)
0)[6] Rojas G, Loewen M R. Fiber-optic probe measurements of void fraction and bubble size distributions beneath breaking waves. Experiments in Fluids, 2007, 43(6): 895-906. DOI:10.1007/s00348-007-0356-5 (
 0)
0)[7] Blenkinsopp C E, Chaplin J R. Bubble size measurements in breaking waves using optical fiber phase detection probes. IEEE Journal of Oceanic Engineering, 2010, 35(2): 388-401. DOI:10.1109/joe.2010.2044940 (
 0)
0)[8] Rapp R J, Melville W K. Laboratory measurements of deep-water breaking waves. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1990, 331(1622): 735-800. DOI:10.1098/rsta.1990.0098 (
 0)
0)[9] Lin J C, Rockwell D. Evolution of a quasi-steady breaking wave. Journal of Fluid Mechanics, 1995, 302(302): 29-44. DOI:10.1017/S0022112095003995 (
 0)
0)[10] Loewen M R, O'Dor M A, Skafel M G. Bubbles entrained by mechanically generated breaking waves. Journal of Geophysical Research: Oceans, 1996, 101(C9): 20759-20769. DOI:10.1029/96jc01919 (
 0)
0)[11] Bonmarin P. Geometric properties of deep-water breaking waves. Journal of Fluid Mechanics, 1989, 209: 405-433. DOI:10.1017/S0022112089003162 (
 0)
0)[12] Qiao H, Duncan J H. Gentle spilling breakers: Crest flow-field evolution. Journal of Fluid Mechanics, 2001, 439: 57-85. DOI:10.1017/S0022112001004207 (
 0)
0)[13] Grue J, Jensen A. Experimental velocities and accelerations in very steep wave events in deep water. European Journal of Mechanics, B/Fluids, 2006, 25(5): 554-564. DOI:10.1016/j.euromechflu.2006.03.006 (
 0)
0)[14] Duncan J H. An experimental investigation of breaking waves produced by a towed hydrofoil. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1981, 377(1770): 331-348. DOI:10.1098/rspa.1981.0127 (
 0)
0)[15] Duncan J H. The breaking and non-breaking wave resistance of a two-dimensional hydrofoil. Journal of Fluid Mechanics, 1983, 126: 507-520. DOI:10.1017/S0022112083000294 (
 0)
0)[16] Chang K A, Liu L F. Experimental investigation of turbulence generated by breaking waves in water of intermediate depth. Physics of Fluids, 1999, 11(11): 3390-3400. DOI:10.1063/1.870198 (
 0)
0)[17] Kimmoun O, Branger H. A particle image velocimetry investigation on laboratory surf-zone breaking waves over a sloping beach. Journal of Fluid Mechanics, 2007, 588: 353-397. DOI:10.1017/S0022112007007641 (
 0)
0)[18] Lamarre E, Melville W K. Air entrainment and dissipation in breaking waves. Nature, 1991, 351: 469-472. DOI:10.1038/351469a0 (
 0)
0)[19] Lamarre E, Melville W K. Void-fraction measurements and sound-speed fields in bubble plumes generated by breaking waves. The Journal of the Acoustical Society of America, 1994, 95(3): 1317-1328. DOI:10.1121/1.408572 (
 0)
0)[20] Cartmill J W, Su M Y. Bubble size distribution under saltwater and freshwater breaking waves. Dynamics of Atmospheres and Oceans, 1993, 20(1-2): 25-31. DOI:10.1016/0377-0265(93)90046-A (
 0)
0)[21] Mori N, Kakuno S. Aeration and bubble measurements of coastal breaking waves. Fluid Dynamics Research, 2008, 40(7-8): 616-626. DOI:10.1016/j.fluiddyn.2007.12.013 (
 0)
0)[22] Blenkinsopp C E, Chaplin J R. Void fraction measurements in breaking waves. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 463(2088): 3151-3170. DOI:10.1098/rspa.2007.1901 (
 0)
0)[23] Andreas E L. A new sea spray generation function for wind speeds up to 32 m s-1. Journal of Physical Oceanography, 1998, 28(11): 2175-2184. 2.0.CO;2" target="_blank" title="点击浏览原文">DOI:10.1175/1520-0485(1998)028<2175:ANSSGF>2.0.CO;2 (
 0)
0)[24] Veron F, Hopkins C, Harrison E L, et al. Sea spray spume droplet production in high wind speeds. Geophysical Research Letters, 2012, 39(16): L16602(1-5). DOI:10.1029/2012GL052603 (
 0)
0)[25] Towle D M. Spray Droplet Generation by Breaking Water Waves. College Park: University of Maryland, 2014. (
 0)
0)[26] Scardovelli R, Zaleski S. Direct numerical simulation of free-surface and interfacial flow. Annual Review of Fluid Mechanics, 1999, 31(1): 567-603. DOI:10.1146/annurev.fluid.31.1.567 (
 0)
0)[27] Lemos C M. Wave Breaking: A Numerical Study. Berlin: Springer-Verlag, 2013. (
 0)
0)[28] Takikawa K. Internal characteristics and numerical analysis of plunging breaker on a slope. Coastal Engineering, 1997, 31(1-4): 143-161. DOI:10.1016/S0378-3839(97)00003-3 (
 0)
0)[29] Lin P, Liu L F. A numerical study of breaking waves in the surf zone. Journal of Fluid Mechanics, 1998, 359: 239-264. DOI:10.1017/S002211209700846X (
 0)
0)[30] Lin P, Liu Philip L F. Turbulence transport, vorticity dynamics, and solute mixing under plunging breaking waves in surf zone. Journal of Geophysical Research: Oceans, 1998, 103(C8): 15677-15694. DOI:10.1029/98JC01360 (
 0)
0)[31] Bradford S F. Numerical simulation of surf zone dynamics. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2000, 126(1): 1-13. DOI:10.1061/(ASCE)0733-950X(2000)126:1(1) (
 0)
0)[32] Hieu P D, Katsutoshi T, Ca V T. Numerical simulation of breaking waves using a two-phase flow model. Applied Mathematical Modelling, 2004, 28(11): 983-1005. DOI:10.1016/j.apm.2004.03.003 (
 0)
0)[33] Zhao Q, Armfield S, Tanimoto K. Numerical simulation of breaking waves by a multi-scale turbulence model. Coastal Engineering, 2004, 51(1): 53-80. DOI:10.1016/j.coastaleng.2003.12.002 (
 0)
0)[34] Shi F, Kirby J T, Ma G. Modeling quiescent phase transport of air bubbles induced by breaking waves. Ocean Modelling, 2010, 35(1-2): 105-117. DOI:10.1016/j.ocemod.2010.07.002 (
 0)
0)[35] Liang J H, McWilliams J C, Sullivan P P, et al. Modeling bubbles and dissolved gases in the ocean. Journal of Geophysical Research Oceans, 2011, 116(C3): C03015(1-17). DOI:10.1029/2010JC006579 (
 0)
0)[36] Liang J H, McWilliams J C, Sullivan P P, et al. Large eddy simulation of the bubbly ocean: New insights on subsurface bubble distribution and bubble-mediated gas transfer. Journal of Geophysical Research, 2012, 117(C4): C04002. DOI:10.1029/2011jc007766 (
 0)
0)[37] Derakhti M, Kirby J T. Bubble entrainment and liquid-bubble interaction under unsteady breaking waves. Journal of Fluid Mechanics, 2014, 761: 464-506. DOI:10.1017/jfm.2014.637 (
 0)
0)[38] Zhao Q, Tanimoto K. Numerical simulation of breaking waves by large eddy simulation and VOF method. 26th International Conference on Coastal Engineering. Restion VA:ASCE, 1998, 1(26): 892-905. DOI:10.1061/9780784404119.066 (
 0)
0)[39] Watanabe Y, Saeki H. Three-dimensional large eddy simulation of breaking waves. Coastal Engineering Journal, 1999, 41(3-4): 281-301. DOI:10.1142/S0578563499000176 (
 0)
0)[40] Mutsuda H, Yasuda T. Numerical simulation of turbulent air-water mixing layer within surf-zone. Proceedings of the 27th International Conference on Coastal Engineering. Restion VA:ASCE, 2000, 755-768. DOI:10.1061/40549(276)59 (
 0)
0)[41] Christensen E D, Deigaard R. Large eddy simulation of breaking waves. Coastal Engineering, 2001, 42(1): 53-86. DOI:10.1016/S0378-3839(00)00049-1 (
 0)
0)[42] Watanabe Y, Saeki H, Hosking R. Three-dimensional vortex structures under breaking waves. Journal of Fluid Mechanics, 2005, 545: 291-328. DOI:10.1017/S0022112005006774 (
 0)
0)[43] Lubin P, Vincent Stéphane, Caltagirone J P, et al. Fully three-dimensional direct numerical simulation of a plunging breaker. Comptes Rendus Mécanique, 2003, 331(7): 495-501. DOI:10.1016/S1631-0721(03)00108-6 (
 0)
0)[44] Biausser B, Fraunié P, Grilli T, et al. Numerical analysis of the internal kinematics and dynamics of three-dimensional breaking waves on slopes. International Journal of Offshore and Polar Engineering, 2004, 14(4): 247-256. (
 0)
0)[45] Chen G, Kharif C, Zaleski S, et al. Two-dimensional Navier-Stokes simulation of breaking waves. Physics of Fluids, 1999, 11(1): 121-133. DOI:10.1063/1.869907 (
 0)
0)[46] Song C, Sirviente A I. A numerical study of breaking waves. Physics of Fluids, 2004, 16(7): 2649-2667. DOI:10.1063/1.1738417 (
 0)
0)[47] Hendrickson K, Yue D K P. Navier-Stokes simulations of unsteady small-scale breaking waves at a coupled air-water interface. Proceedings of the Twenty-Sixth Symposium on Naval Hydrodynamics Office of Naval Research, 2006. (
 0)
0)[48] Iafrati A. Energy dissipation mechanisms in wave breaking processes: Spilling and highly aerated plunging breaking events. Journal of Geophysical Research: Oceans, 2011, 116(C7): C07024(1-22). DOI:10.1029/2011JC007038 (
 0)
0)[49] Deike L, Popinet S, Melville W K. Capillary effects on wave breaking. Journal of Fluid Mechanics, 2015, 769: 541-569. DOI:10.1017/jfm.2015.103 (
 0)
0)[50] Iafrati A. Numerical study of the effects of the breaking intensity on wave breaking flows. Journal of Fluid Mechanics, 2009, 622: 371-411. DOI:10.1017/S0022112008005302 (
 0)
0)[51] Iafrati A. Air-water interaction in breaking wave events: quantitative estimates of drops and bubbles. Proceedings of 28th Symposium on Naval Hydrodynamics. Pasadena. California. 2010.12-17. (
 0)
0)[52] Kang D, Ghosh S, Reins G, et al. Impulsive plunging wave breaking downstream of a bump in a shallow water flume—Part Ⅰ: Experimental observations. Journal of Fluids and Structures, 2012, 32: 104-120. DOI:10.1016/j.jfluidstructs.2011.10.010 (
 0)
0)[53] Koo B, Wang Z, Yang J, et al. Impulsive plunging wave breaking downstream of a bump in a shallow water flume—Part Ⅱ: Numerical simulations. Journal of Fluids and Structures, 2012, 32: 121-134. DOI:10.1016/j.jfluidstructs.2011.10.011 (
 0)
0)[54] Thorpe S A. Langmuir circulation. Annual Review of Fluid Mechanics, 2004, 36(36): 55-79. DOI:10.1146/annurev.fluid.36.052203.071431 (
 0)
0)[55] Sullivan P P, McWilliams J C, Melville W K, et al. The oceanic boundary layer driven by wave breaking with stochastic variability. Part 1. Direct numerical simulations. Journal of Fluid Mechanics, 2004, 507: 143-174. DOI:10.1017/S0022112004008882 (
 0)
0)[56] Sullivan P P, McWilliams J C, Melville W K. Surface gravity wave effects in the oceanic boundary layer: Large-eddy simulation with vortex force and stochastic breakers. Journal of Fluid Mechanics, 2007, 593: 405-452. DOI:10.1017/S002211200700897X (
 0)
0)[57] Christensen E D. Large eddy simulation of spilling and plunging breakers. Coastal Engineering, 2006, 53(5-6): 463-485. DOI:10.1016/j.coastaleng.2005.11.001 (
 0)
0)[58] Fuster D, Agbaglah G, Josserand C, et al. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dynamics Research, 2009, 41(6): 065001. DOI:10.1088/0169-5983/41/6/065001 (
 0)
0)[59] Brucker K A, O'Shea T T, Dommermuth D G, et al. Three-dimensional simulations of deep-water breaking Waves. The Proceedings of the 28th Symposium on Naval Hydrodynamics. arXiv, 2010.1-20. (
 0)
0)[60] Lakehal D, Liovic P. Turbulence structure and interaction with steep breaking waves. Journal of Fluid Mechanics, 2011, 674: 522-577. DOI:10.1017/jfm.2011.3 (
 0)
0)[61] Zhou Z, Sangermano J, Hsu T J, et al. A numerical investigation of wave-breaking-induced turbulent coherent structure under a solitary wave. Journal of Geophysical Research: Oceans, 2014, 119(10): 6952-6973. DOI:10.1002/2014jc009854 (
 0)
0)[62] Lubin P, Glockner S. Numerical simulations of three-dimensional plunging breaking waves: Generation and evolution of aerated vortex filaments. Journal of Fluid Mechanics, 2015, 767: 364-393. DOI:10.1017/jfm.2015.62 (
 0)
0)[63] Stern F, Wang Z, Yang J, et al. Recent progress in CFD for naval architecture and ocean engineering. Journal of Hydrodynamics, 2015, 27(1): 1-23. DOI:10.1016/S1001-6058(15)60452-8 (
 0)
0)[64] Wang Z, Yang J, Stern F. High-fidelity simulations of bubble, droplet and spray formation in breaking waves. Journal of Fluid Mechanics, 2016, 792: 307-327. DOI:10.1017/jfm.2016.87 (
 0)
0)[65] Lubin P, Vincent S, Abadie S, et al. Three-dimensional large eddy simulation of air entrainment under plunging breaking waves. Coastal Engineering, 2006, 53(8): 631-655. DOI:10.1016/j.coastaleng.2006.01.001 (
 0)
0)[66] Kiger K T, Duncan J H. Air-entrainment mechanisms in plunging jets and breaking waves. Annual Review of Fluid Mechanics, 2012, 44(1): 563-596. DOI:10.1146/annurev-fluid-122109-160724 (
 0)
0)[67] Deike L, Melville W K, Popinet S. Air entrainment and bubble statistics in breaking waves. Journal of Fluid Mechanics, 2016, 801: 91-129. DOI:10.1017/jfm.2016.372 (
 0)
0)[68] Rojas G, Loewen M R. Void fraction measurements beneath plunging and spilling breaking waves. Journal of Geophysical Research: Oceans, 2010, 115(C8): C08001. DOI:10.1029/2009JC005614 (
 0)
0)[69] Banner M L, Peirson W L. Wave breaking onset and strength for two-dimensional deep-water wave groups. Journal of Fluid Mechanics, 2007, 585: 93-115. DOI:10.1017/S0022112007006568 (
 0)
0)[70] Drazen D A, Melville W K, Lenain L. Inertial scaling of dissipation in unsteady breaking waves. Journal of Fluid Mechanics, 2008, 611: 307-332. DOI:10.1017/S0022112008002826 (
 0)
0)[71] Grare L, Peirson W L, Branger H, et al. Growth and dissipation of wind-forced, deep-water waves. Journal of Fluid Mechanics, 2013, 722: 5-50. DOI:10.1017/jfm.2013.88 (
 0)
0)[72] Phillips O M. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. Journal of Fluid Mechanics, 1985, 156: 505-531. DOI:10.1017/S0022112085002221 (
 0)
0)[73] Gemmrich J R, Banner M L, Garrett C, et al. Spectrally resolved energy dissipation rate and momentum flux of breaking waves. Journal of Physical Oceanography, 2008, 38(6): 1296-1312. DOI:10.1175/2007jpo3762.1 (
 0)
0)[74] Kleiss J M, Melville W K. Observations of wave breaking kinematics in fetch-limited seas. Journal of Physical Oceanography, 2010, 40(12): 2575-2604. DOI:10.1175/2010jpo4383.1 (
 0)
0)[75] Sutherland Peter, Melville W K, et al. Field measurements and scaling of ocean surface wave-breaking statistics. Geophysical Research Letters, 2013, 40(12): 3074-3079. DOI:10.1002/grl.50584 (
 0)
0)[76] Romero L, Melville W K, Kleiss J M. Spectral energy dissipation due to surface wave breaking. Journal of Physical Oceanography, 2012, 42(9): 1421-1444. DOI:10.1175/jpo-d-11-072.1 (
 0)
0)[77] Garrett C, Li M, Farmer D. The connection between bubble size spectra and energy dissipation rates in the upper ocean. Journal of Physical Oceanography, 2000, 30(9): 2163-2171. 2.0.CO;2" target="_blank" title="点击浏览原文">DOI:10.1175/1520-0485(2000)030<2163:TCBBSS>2.0.CO;2 (
 0)
0)[78] Pizzo N E, Melville W K. Vortex generation by deep-water breaking waves. Journal of Fluid Mechanics, 2013, 734: 198-218. DOI:10.1017/jfm.2013.453 (
 0)
0)[79] Melville W K, Fedorov A V. The equilibrium dynamics and statistics of gravity-capillary waves. Journal of Fluid Mechanics, 2015, 767: 449-466. DOI:10.1017/jfm.2014.740 (
 0)
0)[80] Herrmann M. A parallel Eulerian interface tracking/Lagrangian point particle multi-scale coupling procedure. Journal of Computational Physics, 2010, 229(3): 745-759. DOI:10.1016/j.jcp.2009.10.009 (
 0)
0)[81] Soloviev A, Lukas R. The Near-Surface Layer of the Ocean: Structure, Dynamics and Applications. Berlin: Springer, 2006. DOI:10.1007/1-4020-4053-9 (
 0)
0)[82] Tavakolinejad M. Air Bubble Entrainment by Breaking bow Waves Simulated by a 2D+T Technique. Maryland: University of Maryland, 2010. (
 0)
0)[83] Lhuissier H, Villermaux E. Bursting bubble aerosols. Journal of Fluid Mechanics, 2012, 696: 5-44. DOI:10.1017/jfm.2011.418 (
 0)
0)[84] Terrill E J, Melville W K, Stramski D. Bubble entrainment by breaking waves and their influence on optical scattering in the upper ocean. Journal of Geophysical Research Oceans, 2001, 106(C8): 16815-16823. DOI:10.1029/2000jc000496 (
 0)
0)[85] Liu X, Duncan J H. The effects of surfactants on spilling breaking waves. Nature, 2003, 421(6922): 520-523. DOI:10.1038/nature01357 (
 0)
0)[86] Liu X, Duncan J H. An experimental study of surfactant effects on spilling breakers. Journal of Fluid Mechanics, 2006, 567: 433-455. DOI:10.1017/S0022112006002011 (
 0)
0)[87] Duncan J H. Spilling breaker. Annual Review of Fluid Mechanics, 2001, 33(33): 519-547. DOI:10.1146/annurev.fluid.33.1.519 (
 0)
0)[88] Perlin M, Choi W, Tian Z. Breaking waves in deep and intermediate waters. Annual Review of Fluid Mechanics, 2013, 45(1): 115-145. DOI:10.1146/annurev-fluid-011212-140721 (
 0)
0)[89] Longuet-Higgins M S. Capillary rollers and bores. Journal of Fluid Mechanics, 1992, 240(1): 659-679. DOI:10.1017/S0022112092000259 (
 0)
0)[90] Iafrati A, Babanin A, Onorato M. Modulational instability, wave breaking, and formation of large-scale dipoles in the atmosphere. Physical Review Letters, 2013, 110(18): 184504. DOI:10.1103/PhysRevLett.110.184504 (
 0)
0)[91] Yang Z, Deng B, Shen L. Direct numerical simulation of wind turbulence over breaking waves. Journal of Fluid Mechanics, 2018, 850: 120-155. DOI:10.1017/jfm.2018.466 (
 0)
0)[92] Mitroglou N, Lorenzi M, Santini M, et al. Application of X-ray micro-computed tomography on high-speed cavitating diesel fuel flows. Experiments in Fluids, 2016, 57(11): 175. DOI:10.1007/s00348-016-2256-z (
 0)
0)[93] Liu C, Hu C. An immersed boundary solver for inviscid compressible flows. International Journal for Numerical Methods in Fluids, 2017, 85(11): 619-640. DOI:10.1002/fld.4399 (
 0)
0)[94] Liu C, Hu C. An adaptive multi-moment FVM approach for incompressible flows. Journal of Computational Physics, 2018, 359: 239-262. DOI:10.1016/j.jcp.2018.01.006 (
 0)
0)[95] Liu C, Hu C. Adaptive THINC-GFM for compressible multi-medium flows. Journal of Computational Physics, 2017, 342: 43-65. DOI:10.1016/j.jcp.2017.04.032 (
 0)
0)[96] Liu C, Hu C. Block-based adaptive mesh refinement for fluid-structure interactions in incompressible flows. Computer Physics Communication, 2018, 232: 104-123. DOI:10.1016/j.cpc.2018.05.015 (
 0)
0)