基于动态T-S模糊控制的视觉目标跟随

郑晶翔,曹博,毕树生,杨东升

(北京航空航天大学 机械工程及自动化学院, 北京 100191)



摘要:

针对基于传统线性控制律的移动机器人视觉目标跟随系统的角度误差控制无法满足高效和快速的要求,进而容易丢失目标的问题,提出基于动态T-S模糊控制的视觉跟随方法. 利用HOG算法检测目标,并结合摄像机模型获取目标位置向量,在T-S模糊控制律的基础上进行动态化处理,进一步提高角度误差收敛的响应速度. MATLAB仿真表明:角度误差的收敛时间小于0.4 s,改进的模糊控制可以有效提高角度误差的响应速度,缩短角度误差收敛的时间,使得跟随系统具有较好的快速性和适应性. 在移动机器人平台上进行跟随实验,得到的角度误差收敛时间也小于0.5 s. 基于动态T-S模糊控制的移动机器人视觉跟随系统对角度误差能够快速响应并达到收敛,进而有效防止跟随目标的丢失.

关键词:  视觉检测  HOG特征  T-S模糊  移动机器人  目标跟随

DOI：10.11918/j.issn.0367-6234.201803093

分类号:TP242.6

文献标识码:A

基金项目:



Visual target tracking based on dynamic fuzzy-model control

ZHENG Jingxiang,CAO Bo,BI Shusheng,YANG Dongsheng

(School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China)

Abstract:

The problem, that the angle control of the mobile robot's visual target following system based on the traditional linear control law cannot satisfy the need of high efficiency and fastness so that the target is easy missed, is focused in this paper. A visual following method based on dynamic T-S fuzzy control is proposed. The HOG algorithm is used to detect the target and the target position vector is obtained by the camera model. Based on the T-S fuzzy control, dynamic processing is performed to further improve the response speed of angular error convergence. The simulation by MATLAB shows that the convergence time of the angle error is less than 0.4 second. Therefore, the improved fuzzy control method can effectively improve the response speed of the angle error, shorten the time of the angle error convergence, and make the follow-up system have better rapidity and adaptability. By experiment on the mobile robot platform, the convergence time of the angle error is less than 0.5 second.

Key words:  visual inspection  HOG feature  T-S fuzzy  Wheel Mobile Robot  target tracking


郑晶翔, 曹博, 毕树生, 杨东升. 基于动态T-S模糊控制的视觉目标跟随[J]. 哈尔滨工业大学学报, 2019, 51(1): 178-183. DOI: 10.11918/j.issn.0367-6234.201803093.
ZHENG Jingxiang, CAO Bo, BI Shusheng, YANG Dongsheng. Visual target tracking based on dynamic fuzzy-model control[J]. Journal of Harbin Institute of Technology, 2019, 51(1): 178-183. DOI: 10.11918/j.issn.0367-6234.201803093.
作者简介 郑晶翔(1995—)，男，硕士研究生 通信作者 郑晶翔, 13521419905@163.com 文章历史 收稿日期: 2018-03-16



Contents            -->Abstract            Full text            Figures/Tables            PDF


基于动态T-S模糊控制的视觉目标跟随
郑晶翔, 曹博, 毕树生, 杨东升    
北京航空航天大学 机械工程及自动化学院，北京 100191

收稿日期: 2018-03-16
作者简介: 郑晶翔(1995—)，男，硕士研究生
通信作者: 郑晶翔, 13521419905@163.com


摘要: 针对基于传统线性控制律的移动机器人视觉目标跟随系统的角度误差控制无法满足高效和快速的要求，进而容易丢失目标的问题，提出基于动态T-S模糊控制的视觉跟随方法.利用HOG算法检测目标，并结合摄像机模型获取目标位置向量，在T-S模糊控制律的基础上进行动态化处理，进一步提高角度误差收敛的响应速度. MATLAB仿真表明：角度误差的收敛时间小于0.4 s，改进的模糊控制可以有效提高角度误差的响应速度，缩短角度误差收敛的时间，使得跟随系统具有较好的快速性和适应性.在移动机器人平台上进行跟随实验，得到的角度误差收敛时间也小于0.5 s.基于动态T-S模糊控制的移动机器人视觉跟随系统对角度误差能够快速响应并达到收敛，进而有效防止跟随目标的丢失.
关键词: 视觉检测    HOG特征    T-S模糊    移动机器人    目标跟随    
Visual target tracking based on dynamic fuzzy-model control
ZHENG Jingxiang, CAO Bo, BI Shusheng, YANG Dongsheng    
School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China


Abstract: The problem, that the angle control of the mobile robot's visual target following system based on the traditional linear control law cannot satisfy the need of high efficiency and fastness so that the target is easy missed, is focused in this paper. A visual following method based on dynamic T-S fuzzy control is proposed. The HOG algorithm is used to detect the target and the target position vector is obtained by the camera model. Based on the T-S fuzzy control, dynamic processing is performed to further improve the response speed of angular error convergence. The simulation by MATLAB shows that the convergence time of the angle error is less than 0.4 second. Therefore, the improved fuzzy control method can effectively improve the response speed of the angle error, shorten the time of the angle error convergence, and make the follow-up system have better rapidity and adaptability. By experiment on the mobile robot platform, the convergence time of the angle error is less than 0.5 second.
Keywords: visual inspection    HOG feature    T-S fuzzy    Wheel Mobile Robot    target tracking    
移动机器人目标跟随可以分为两个环节：一部分是目标位置的获取，另一部分是机器人的跟随控制.当前一部分关于目标跟随的文章关注的是视觉检测领域^[1]，他们将关注点集中在对动态目标的捕捉上，着重提高对环境的适应性以及算法的高效性^[2].也有一些文章将目标跟随应用在移动机器人上，其中大部分基于测距传感器^[3], 包括激光雷达和超声波传感器，另外一部分则基于视觉传感器.相比于测距传感器，视觉传感器具有诸多优势，包括目标不需要携带设备，对中间障碍物的遮挡有一定的鲁棒性等.但是目前应用视觉跟随的移动机器人都存在一个共性问题^[4]：现在市场上主流相机的视场角都在60°左右，而机器人跟随的目标必须位于相机视场范围内，这就导致目标相对于机器人的横向移动速度不能过快，否则机器人极易丢失目标，从而在一定程度上限制了视觉跟随在实际中的应用^[5].

与此同时，移动机器人的控制系统设计已经有相对成熟的研究.在笛卡尔坐标系下，移动机器人的控制为非完整约束；在极坐标系下，其运动学模型可以被表示为距离和角度变量，通过控制输入将系统转化为完整约束^[6].由于控制系统与角度相关，因此将其进行线性化处理，与非线性控制设计相比，模糊控制更加简单、直观.通过扇形非线性方法，移动机器人的极坐标运动模型可以精确地转化为T-S模糊模型^[7]，并且可以使得系统具有较好的稳定性.在此基础上，Chung-Hsun Sun等^[8]利用多模式转换的思想控制机器人接近目标点，可以获得一条更优的跟随路线，但是跟随过程是非连续的，同时需要对模式转换点进行识别.

本文设计实现了一种基于视觉目标检测的移动机器人自主跟随控制系统.该系统利用HOG特征进行目标检测，进而获取其位置向量，然后利用改进的模糊控制律对速度输入进行实时计算，从而使移动机器人以高效、快速且连续的轨迹跟随目标.为了进一步提高控制系统对于角度误差的响应速度，提出动态化角度控制律的思想，进而能更加有效地解决移动机器人视觉跟随中容易丢失目标的问题，通过仿真和实验验证了控制系统的有效性.

1 基于行人检测的跟随模型目前常用的行人检测方法^[9]有如下几种：Harr-like、Edgelet特征、Shapelet特征、LBP特征和HOG特征，此外还有基于轮廓模板的方法和基于运动特征的方法^[10].本文选取的HOG特征是目前应用最为广泛的行人特征^[11].

假设图像平面与目标所在的平面平行，摄像机水平安装，且处于机器人的中心，可以得到如图 1所示的参数关系图，根据相似三角形关系可以得到实际距离x, y与图像测量值Δh, Δδ之间的关系式：

$\frac{f}{y} = \frac{{{k_c}{k_h}\Delta h}}{H} = \frac{{{k_c}\Delta \delta }}{x}.$ (1)

Figure 1
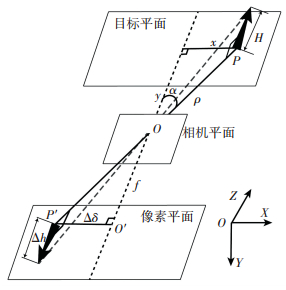图 1 行人检测的各项参数 Figure 1 Parameters of human detection


式中：f为焦距，ρ为实际距离误差，α为实际角度误差，Δh为目标高度所占像素，Δδ为目标偏移距离所占像素，H为目标实际高度，x为实际偏移距离，y为实际垂直距离，k_h为高度修正系数，k_c为像素转化系数.

根据式(1)可得目标实际距离为

$\left\{ \begin{array}{l}x = \frac{{H\Delta \delta }}{{{k_h}\Delta h}},\\y = \frac{{fH}}{{{k_c}{k_h}\Delta h}}.\end{array} \right.$ (2)

根据直角三角形的几何关系可以算出目标的位置向量为

$\left( {\begin{array}{*{20}{c}}\rho \\\alpha \end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\sqrt {{x^2} + {y^2}} }\\{\arctan \frac{x}{y}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{H}{{{k_h}\Delta h}}\sqrt {\Delta {\delta ^2} + {{\left( {\frac{f}{{{k_c}}}} \right)}^2}} }\\{\arctan \frac{{{k_c}\Delta \delta }}{f}}\end{array}} \right).$ (3)

本系统选取的实验对象是四轮驱动移动机器人，L为左右轮之间的间距，通过引入滑移率χ，可以得到如下的运动学模型^[12]：

$\left( {\begin{array}{*{20}{c}}{{v_x}}\\{{v_y}}\\\omega \end{array}} \right) = \frac{1}{{\chi L}} \cdot \left( {\begin{array}{*{20}{c}}{\frac{{\chi L}}{2}}&{\frac{{\chi L}}{2}}\\0&0\\{ - 1}&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{v_l}}\\{{v_r}}\end{array}} \right).$ (4)

设(X_R, Y_R)为机器人参考系，(X_T，Y_T)为目标参考系.目标位置向量为[ρ α β]^T，移动机器人动态目标跟随模型如图 2所示^[13].根据数学几何关系式：α=-θ+arctan2(Δy, Δx), β=-θ-α和$\rho = \sqrt {\Delta {x^2} + \Delta {y^2}} $可以得到机器人的速度为

$\left[ {\begin{array}{*{20}{c}}{\dot \rho }\\{\dot \alpha }\\{\dot \beta }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - \cos \alpha }&0\\{\frac{{\sin \alpha }}{\rho }}&{ - 1}\\{ - \frac{{\sin \alpha }}{\rho }}&0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}v\\\omega \end{array}} \right].$ (5)

Figure 2
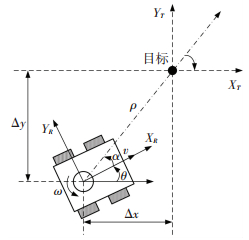图 2 动态目标跟随模型 Figure 2 Dynamic target tracking model


轮式移动机器人跟随的传统线性控制律为

$\left\{ \begin{array}{l}v = {k_\rho }\rho ,\\\omega = {k_\alpha }\alpha + {k_\beta }\beta .\end{array} \right.$ (6)

式中k_ρ、k_α和k_β分别是跟随目标的位置ρ、方位角α、航向角β的比例系数.将式(6)代入式(5)可以得到极坐标系下机器人的速度为

$\left[ {\begin{array}{*{20}{c}}{\dot \rho }\\{\dot \alpha }\\{\dot \beta }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - {k_\rho }\rho \cos \alpha }\\{{k_\rho }\sin \alpha - {k_\alpha }\alpha - {k_\beta }\beta }\\{ - {k_\rho }\sin \alpha }\end{array}} \right].$ (7)

2 动态T-S模糊控制上述速度方程中的sin α和cos α是非线性函数，如果使用局部线性化的方法，则可以接受的近似误差只存在于一个小区域中(角度值较小时).通过采用扇形非线性方法，非线性项可以精确地表示为一组模糊组合，所以本系统以T-S模糊模型为基础设计移动机器人的控制系统^[14].

T-S模糊系统：z₁(t)是M_i1, z_p(t)是M_ip.

$\mathit{\boldsymbol{\dot y}}\left( t \right) = {\mathit{\boldsymbol{A}}_i}y\left( t \right) + {\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{u}}\left( t \right),i = 1,2, \cdots ,r.$ (8)

式中：M_ip是模糊集合，r是模糊规则的数量；y (t)∈ Rⁿ是状态向量，u (t)∈ R^m是控制输入向量, z₁(t)到z_p(t)是已知的外部向量，A_i, B_i为控制矩阵.

给定(y (t), u (t))，得到模糊系统的输出为

$\mathit{\boldsymbol{\dot y}} = \frac{{\sum\limits_{i = 1}^r {{w_i}\left( {\mathit{\boldsymbol{z}}\left( t \right)} \right)\left[ {{\mathit{\boldsymbol{A}}_i}y\left( t \right) + {\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{u}}\left( t \right)} \right]} }}{{\sum\limits_{i = 1}^r {{w_i}\left( {\mathit{\boldsymbol{z}}\left( t \right)} \right)} }},$ (9)

${w_i}\left( {z\left( t \right)} \right) = \prod\limits_{j = 1}^p {{M_{ij}}\left( {{z_j}\left( t \right)} \right)} ,$ (10)

${\mu _i}\left( {z\left( t \right)} \right) = \frac{{{w_i}\left( {z\left( t \right)} \right)}}{{\sum\limits_{i = 1}^r {{w_i}\left( {z\left( t \right)} \right)} }}.$ (11)

式中:w_i(z(t))为隶属度，μ_i(z(t))为模糊权重.特别的，有$\sum\limits_{i = 1}^r {{\mu _i}\left( {z\left( t \right)} \right)} = 1$.

针对式(7)中的sin α和cos α进行处理^[15]：

$\left\{ \begin{array}{l}{s_2} \cdot \alpha \le \sin \alpha \le {s_1} \cdot \alpha ,0 \le \alpha < {\rm{ \mathsf{ π} }}/2,\\{s_1} \cdot \alpha \le \sin \alpha \le {s_2} \cdot \alpha , - {\rm{ \mathsf{ π} }}/2 \le \alpha < 0.\end{array} \right.$ (12)

${c_2} \le \cos \alpha \le {c_1},\left| \alpha \right| < {\rm{ \mathsf{ π} }}/2.$ (13)

式中c₁=1, c₂=π/100, s₁=1, s₂=π/2.

当α满足式(12)和式(13)时，非线性系统模型可以表示为

$\left\{ \begin{array}{l}{n_1} = \cos \alpha = {\rm{T}}{{\rm{C}}_1}\left( {{n_1}} \right) \cdot {c_1} + {\rm{T}}{{\rm{C}}_2}\left( {{n_2}} \right) \cdot {c_2},\\{n_2} = \sin \alpha = {\rm{T}}{{\rm{S}}_1}\left( {{n_2}} \right) \cdot {s_1} + {\rm{T}}{{\rm{S}}_2}\left( {{n_2}} \right) \cdot {s_2}.\end{array} \right.$ (14)

式中：${\rm{T}}{{\rm{C}}_1}({n_1}) = \frac{{{n_1} - {c_2}}}{{{c_1} - {c_2}}}$, TC₂(n₁)=1-TC₁(n₁), ${\rm{T}}{{\rm{S}}_1}({n_2}) = \frac{{{n_2} \cdot \sin {n_2} - {s_2}}}{{{s_1} - {s_2}}}$, TS₂(n₂)=1-TS₁(n₂).

此时跟随控制律可以转换成一个包含线性系统的T-S模糊模型：

定义：对于x =[ρ α β]^T, |α| < π/2, i=2× (u－1)+v, {u, v}∈{1, 2}.

${\mathit{\boldsymbol{A}}_i} = \left[ {\begin{array}{*{20}{c}}{{c_u}{k_\rho }}&0&0\\0&{{k_\alpha } - {s_v}{k_p}}&{{k_\beta }}\\0&{{s_v}{k_p}}&0\end{array}} \right]$ (15)

去模糊化后的模糊控制系统可以表示为

$\mathit{\boldsymbol{\dot x}} = \sum\limits_{i = 1}^4 {{\mu _i}{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{x}}} $ (16)

其中${\mathit{\boldsymbol{\dot x}}}$=[η_ρρ η_αα η_ββ]^T，η_ρ、η_α、η_β分别是ρ, α, β的比例系数，模糊权重μ_i=TC_u·TS_v，忽略到达时的位姿，即k_β=0.目标跟随的角度控制律需要与|α|成正比，以提高角度修正的效率.分别利用三次函数、对数函数和对勾函数对k_α进行动态化处理，得到α?(-1.57, 1.57)时的η_α、η_ρ以及ω值如图 3所示.

Figure 3
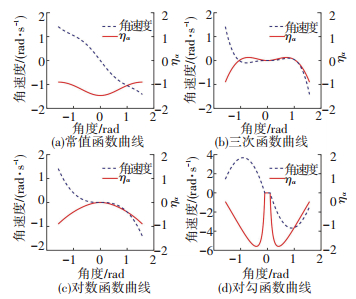图 3 不同参数下的函数值 Figure 3 Function value under different parameters


图 3是用不同函数进行动态化处理时角度控制律η_α和角速度ω的变化曲线.不采用动态化处理时，η_α的整体变化幅度较小，且与|α|成反比.在三次函数或者对数函数约束下，角度误差为1 rad左右就已经保持在较小水平，无法满足快速角度调整的需要.在对勾函数约束下，一定范围内的角度控制律η_α较大且与|α|成反比，将各函数得到的角速度值进行汇总得到图 4.

Figure 4
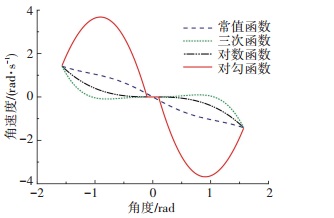图 4 改进的T-S模糊控制对比 Figure 4 Comparison of improved T-S fuzzy control


由于系统需要α较小时，角速度保持在一个较小的水平(趋近于0)，以减少横向的抖动.在α较大时，角速度也较大以快速修正与跟踪目标的角度误差，从而防止目标离开相机视野.从图 4采用4种动态控制律的结果来看，利用对勾函数动态化的控制律在角度误差小于0.05 rad时角速度为0，在角度误差为1 rad时角速度达到峰值，约为3.8 rad/s，符合需要的设计要求.

因此选取对勾函数作为跟随的动态角度控制律，取k_α(α)=γ(aα+b/α+c), γ, a, b, c是对勾函数的参数，根据式(3)和式(16)可得

$\left( \begin{array}{l}v\\\omega \end{array} \right) = \left( \begin{array}{l}\frac{{{\eta _\rho }H}}{{{k_h}\Delta h}}\left( {\frac{{{k_c}\Delta {\delta ^2}}}{f} + \frac{f}{{{k_c}}}} \right)\\\frac{{{\eta _\rho }{k_c}\Delta \delta }}{f} + {\eta _\alpha }\arctan \frac{{{k_c}\Delta \delta }}{f}\end{array} \right).$ (17)

3 仿真与实验 3.1 MATLAB软件仿真在MATLAB软件中，利用上述改进模型进行目标跟随仿真.为验证跟随算法的适应性，选取直线、正弦和圆曲线作为跟随目标的运动轨迹.

给定参考直线的输入为v=0.2 m/s，ω=0, 目标轨迹方程为y=0.5x，机器人的初始位置为[3.53, -0.56, -1.53]^T，可得移动机器人直线轨迹跟踪仿真如图 5所示.

Figure 5
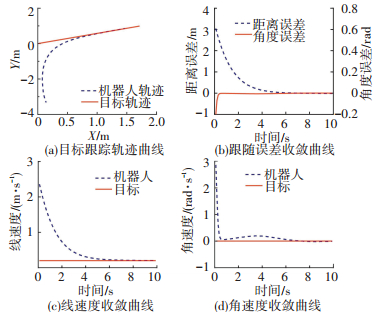图 5 直线轨迹跟踪仿真 Figure 5 Linear trajectory tracking simulation


给定参考圆周的轨迹方程为(x-3)²+y²=4，输入为v=0.2 m/s, ω=0.1 rad/s，机器人初始位置为[3.53, -0.56, -1.53]^T，可得移动机器人圆周轨迹跟踪仿真如图 6所示.

Figure 6
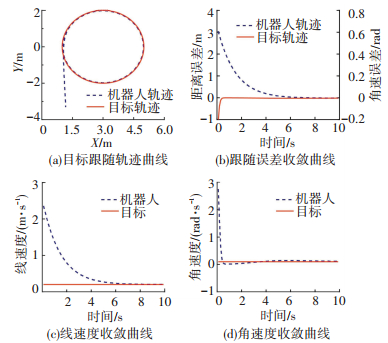图 6 圆周轨迹跟踪仿真 Figure 6 Circular trajectory tracking simulation


对机器人跟随目标过程的各个时间进行统计得到表 1.其中将Ⅰ级定义为误差小于0.1(单位参照SI)时收敛，Ⅱ级定义为误差小于0.01时收敛.

表 1
表 1 仿真实验结果 Table 1 The results of simulation 跟随时间/s 直线 正弦 圆

改进 线性 改进 线性 改进 线性

距离 Ⅰ 4.3 3.8 5.0 4.5 4.8 4.5

Ⅱ 6.8 4.8 8.0 6.2 6.8 6.0

角度 Ⅰ 0.16 29.2 0.14 发散 0.15 6.7

Ⅱ 0.32 50.1 0.34 发散 0.34 18.5

线速度 7.3 4.7 6.7 5.6 7.5 9.0

角速度 7.1 70 8.6 发散 8.9 26



表 1 仿真实验结果 Table 1 The results of simulation


根据仿真结果，在角度误差的收敛速度上，改进的模糊控制只需要0.3 s左右，而线性控制律需要20~50 s，甚至还存在无法收敛的情况，从而表明动态的模糊控制可以使得对角度误差的收敛速度明显提高.通过仿真验证了该系统具有较好的快速性和适应性.

3.2 动态目标跟随实验本实验所使用的是自主研发的falconbot移动机器人平台(见图 7)，搭载xtion pro live摄像机，图像分辨率为640×480，工控机的系统型号是Ubuntu14.04.

Figure 7
图 7 Falconbot移动机器人平台 Figure 7 Falconbot mobile robot platform


通过实验(如图 8)测定式(2)中的相关参数如表 2所示.

Figure 8
图 8 参数测定实验照片 Figure 8 Photo of parametric determination experimental


表 2
表 2 参数测定实验数据 Table 2 Experimental data of parameter determination 实验组号 图片数/张 Δδ Δh 直线/m 偏移/m f/k_c(x) f/k_c(y) 正检率/% 检测效率/%

1 41 21.4 371.7 3.0 0.0 511.0 825.2 91.1 35.4

2 60 17.0 285.7 4.2 0.0 549.9 1 160 90.9 46.2

3 31 149.2 301.6 4.2 0.6 580.4 1 163 83.8 34.9

平均值 547.1 1 049.4 88.6 38.8



表 2 参数测定实验数据 Table 2 Experimental data of parameter determination


由于无法得到摄像机准确的焦距值f，因此直接测定f/k_c.而误差会导致x, y的测量值与实际值存在偏差，为了最大限度地保证模型的可靠性，根据式(2)得到2种测定方式：

$\frac{f}{{{k_c}}} = \frac{{y\Delta \delta }}{x},$

$\frac{f}{{{k_c}}}\left( y \right) = \frac{{y{k_h}\Delta h}}{H}.$

由表 2可知，计算与x相关的参数时，f/k_c取547，而计算与y相关的参数时，f/k_c取1 050，H=1.74 m, k_h=0.797 5.

根据式(2)与式(17)，可以得到跟随的速度为

$\left( \begin{array}{l}v\\\omega \end{array} \right) = \left( \begin{array}{l}\frac{{2.18{\eta _\rho }}}{{\Delta h}}\sqrt {\frac{{\Delta {\delta ^4}}}{{{{10}^6}}} + 1.3\Delta {\delta ^2} + 3 \times {{10}^5}} \\\frac{{{\eta _\rho }\Delta \delta }}{{1\;050}} + {\eta _\alpha }\arctan \frac{{\Delta \delta }}{{1\;050}}\end{array} \right),$

$\left\{ \begin{array}{l}{\eta _\rho } = \sum\limits_u {\sum\limits_v {{c_u}{k_\rho }T{C_u} \cdot T{S_v}} } ,\\{\eta _\alpha } = \sum\limits_u {\sum\limits_v {\left[ {\gamma \left( {a\alpha + \frac{b}{\alpha } + c} \right) - {s_v}{k_\rho }} \right]T{C_u} \cdot T{S_v}} } .\end{array} \right.$

为了评估线性控制律和动态T-S模糊控制律对角度误差的快速性，设计如下对比实验：目标以固定速度沿直线、圆形轨迹以及45°锯齿波轨迹(见图 9)进行运动时，测试在相同参数的控制律作用下移动机器人与目标间角度误差的变化情况.同一组对比实验的初始位置都是相对固定的：直线跟随的起始目标向量为[3.0 m, 0.19 rad]，圆形跟随的起始目标向量为[3.0 m, 0.24 rad], 圆周半径为5 m，锯齿跟随的起始目标向量为[3.0 m, 0.23 rad]，锯齿轨迹的宽度为4 m.

Figure 9
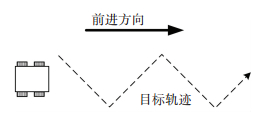图 9 对比实验轨迹示意图 Figure 9 The trajectory of contrast experiment


图 10为目标跟随实验的情况，左上为直线跟随实验，右上为圆周跟随实验，下方为锯齿波跟随实验.利用HOG检测结合式(2)可以得到每一时刻的角度误差值，处理实验过程采集的图像序列，汇总得到如图 11曲线.

Figure 10
图 10 视觉跟随实验照片 Figure 10 Photo of visual following experiment


Figure 11
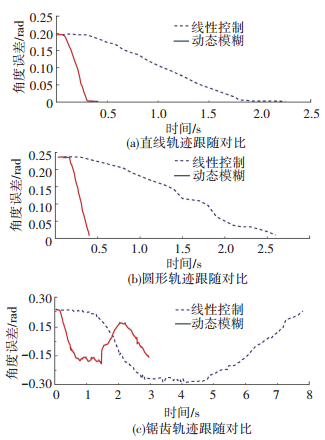图 11 跟随过程中角度误差变化对比 Figure 11 Comparison of angle error changes in following


图 11给出了直线、圆形和锯齿形轨迹的跟随结果，改进后的算法可以在0.5 s内使角度误差收敛至0.01 rad以下，响应速度是线性控制律的四倍左右.另外图 11(c)给出了锯齿波跟随实验的结果，考察其角度误差摆动的范围，一般相机的视场范围为[-0.5, 0.5]，线性控制律的角度摆动范围为[-0.3, 0.27]，动态模糊控制律的角度摆动范围为[-0.18, 0.17]，可以看出改进后的系统可以有效地缩小角度摆动范围，使跟随目标更稳定地处于机器人视野中央.因此系统能够高效地缩小机器人与目标之间的角度误差，有效避免由于目标横向移动过快而使得机器人丢失跟随目标的情况.

4 结论本文详细地描述了利用视觉检测来实现对动态目标实时跟踪的系统，利用HOG检测得到目标的相对位置，利用T-S模糊设计控制系统.为了进一步解决传统控制律在角度修正上的不足，提出了动态化角度控制律的方法，根据仿真的结果选取角度控制效果最好的对勾函数，缩短了角度收敛的时间，进而提高了视觉跟随的稳定性.仿真和实验结果均证明该方法在角度收敛效率上有较大提升，可以有效解决移动机器人视觉跟随在实际应用中容易造成丢失目标的问题.


参考文献
[1] GOREN C C, SARTY M, WU P Y K. Visual following and pattern discrimination of face-like stimuli by newborn infants[J]. Pediatrics, 1975, 56(4): 544.


[2] MAR N J, VAZQUEZ D, LOPEZ A M, et al. Occlusion handling via random subspace classifiers for human detection.[J]. IEEE Transactions on Cybernetics, 2017, 44(3): 342.


[3] SHARMA L, YADAV D K, SINGH A. Fisher's linear discriminant ratio based threshold for moving human detection in thermal video[J]. Infrared Physics & Technology, 2016, 78: 118.


[4] BURKE M G. Visual servo control for human-following robot[D]. Stellenbosch: University of Stellenbosch, 2011: 27


[5] GUEVARA A E, HOAK A, BERNAL JT, et al. Vision-based self-contained target following robot using bayesian data fusion[C]//Advances in Visual Computing. Springer International Publishing, 2016: 846


[6] SUN C H, CHEN Y J, WANG Y T, et al. Sequentially switched fuzzy-model-based control for wheeled mobile robot with visual odometry[J]. Applied Mathematical Modelling, 2016, 47.


[7] TANAKA K, WANG H O. Fuzzy control systems design and analysis: a linear matrix inequality approach[M]. New Jersey: John Wiley & Sons, 2003: 2011.


[8] SUN C H, WANG Y T, CHANG C C. Switching T-S fuzzy model-based guaranteed cost control for two-wheeled mobile robots[J]. International Journal of Innovative Computing, Information and Control, 2012, 8(5): 3015.


[9] DALAL N, TRIGGS B. Histograms of Oriented Gradients for Human Detection[C]//IEEE Computer Society Conference on Computer Vision & Pattern Recognition. San Diego: IEEE Computer Society, 2005: 886


[10] 刘文振.基于HOG特征的行人检测系统的研究[D].南京: 南京邮电大学, 2016
LIU Wenzhen. Research on HOG-based pedestrian detection system[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10293-1016294170.htm


[11] DALAL N, TRIGGS B, SCHMID C. Human detection using oriented histograms of flow and appearance[C]//Computer Vision-ECCV 2006. Berlin Heidelberg: Springer, 2006: 428


[12] YANG Y, WANG H, LIU J, et al. The kinematic analysis and simulation for four-wheel independent drive mobile robot[C]//Control Conference. IEEE, 2011: 3958


[13] ASTOLFI A. Exponential stabilization of a wheeled mobile robot via discontinuous control[J]. Journal of Dynamic Systems Measurement & Control, 1999, 121(1): 121.


[14] ZADEH L A. Fuzzy sets[C]// Fuzzy Sets, Fuzzy Logic, & Fuzzy Systems. World Scientific Publishing Co. Inc., 1996: 394


[15] LAM H, WU L, ZHAO Y. Linear matrix inequalities-based membership function-dependent stability analysis for non-parallel distributed compensation fuzzy-model-based control systems[J]. LET Control Theory & Applications, 2014, 8(8): 614.