刘晓芳2,刘策1,刘露咪3,程丹松1
(1.哈尔滨工业大学 计算机科学与技术学院,哈尔滨 150001; 2.哈尔滨工业大学 电气工程及自动化学院, 哈尔滨 150001; 3.北京控制工程研究所,北京 100000)
摘要:
高斯过程是一种函数的分布,在机器学习领域常用于回归.对于n个训练样本,其训练和预测时间复杂度分别为O(n3)和O(n2),因此难以应用于大规模数据.针对这个问题,本文基于分治的思想,提出一种简单高效的近似模型,称为“重叠局部高斯过程”.本文方法假设随机变量在给定邻近变量的值后,会与距离较远的变量条件独立.首先将训练样本集递归划分,构建一棵三叉树,其中兄弟节点包含的样本存在交集,交集中的样本起到诱导点的作用,可构建相邻区域的依赖关系.然后利用每个叶子结点所包含的样本建立局部的高斯过程回归模型,在当前假设下,每个父节点的边缘似然和预测分布可通过组合其子节点的计算结果来近似,从而降低计算量.同时,这种组合方式可保证拟合的函数是连续的.理论分析表明,对于n个训练样本,近似模型训练和预测的时间复杂度均为O(nt),其中t与交集的大小相关,通常介于1与2之间.此外通过在公共数据集上的实验对比也验证了本文近似模型的有效性.
关键词: 模式识别 高斯过程 回归 贝叶斯学习 大规模机器学习
DOI：10.11918/j.issn.0367-6234.201904056
分类号:TP391.4
文献标识码:A
基金项目:国家自然科学基金(51677042)
Overlapped Local Gaussian Process Regression
LIU Xiaofang2,LIU Ce1,LIU Lumi3,CHENG Dansong1
(1.School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China; 2.School of Electrical Engineering & Automation, Harbin Institute of Technology, Harbin 150001, China; 3.Beijing Institute of Control Engineering, Beijing 100000, China)
Abstract:
Gaussian processes (GPs) are distributions of functions, and are commonly used for regression in machine learning community. For n training samples, their time complexity for training and prediction is O(n3) and O(n2) respectively. The high computational cost hinders their application to large datasets. Inspired by the divide and conquer strategy, the paper proposed a simple but efficient approximate model, called Overlapped Local Gaussian Process (OLGP). The method assumes that given the nearest neighbors, the random variables are independent of farther ones. The training samples are recursively divided and a ternary tree is constructed in the end. Sibling nodes have intersections where the samples play the role of inducing points to model the dependency between neighboring regions. Each leaf node is associated with a local GP regression model. The evidence and predictive distribution in parent nodes are composed of the ones from their sons, which reduces the computational cost significantly. Furthermore, the fitted function is guaranteed to be continuous. A theoretical analysis shows that the time complexity for training and prediction reduces to O(nt) for n training samples, where t depends on the proportion of the intersection in each level, and is usually between 1 and 2. The paper demonstrated the effectiveness of the method by speed-accuracy performance on several real-world datasets.
Key words: pattern recognition gaussian process regression bayesian learning large scale machine learning
刘晓芳, 刘策, 刘露咪, 程丹松. 重叠局部高斯过程回归[J]. 哈尔滨工业大学学报, 2019, 51(11): 22-26. DOI: 10.11918/j.issn.0367-6234.201904056.
LIU Xiaofang, LIU Ce, LIU Lumi, CHENG Dansong. Overlapped Local Gaussian Process Regression[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 22-26. DOI: 10.11918/j.issn.0367-6234.201904056.
基金项目 国家自然科学基金(51677042) 作者简介 刘晓芳(1976—)，女，副教授, 博士 通信作者 程丹松，cdsinhit@hit.edu.cn 文章历史 收稿日期: 2019-04-06
Contents -->Abstract Full text Figures/Tables PDF
重叠局部高斯过程回归
刘晓芳2, 刘策1, 刘露咪3, 程丹松1
1. 哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001;
2. 哈尔滨工业大学 电气工程及自动化学院, 哈尔滨 150001;
3. 北京控制工程研究所, 北京 100000
收稿日期: 2019-04-06
基金项目: 国家自然科学基金(51677042)
作者简介: 刘晓芳(1976—)，女，副教授, 博士
通信作者: 程丹松，cdsinhit@hit.edu.cn
摘要: 高斯过程是一种函数的分布，在机器学习领域常用于回归.对于n个训练样本，其训练和预测时间复杂度分别为O(n3)和O(n2)，因此难以应用于大规模数据.针对这个问题，本文基于分治的思想，提出一种简单高效的近似模型，称为“重叠局部高斯过程”.本文方法假设随机变量在给定邻近变量的值后，会与距离较远的变量条件独立.首先将训练样本集递归划分，构建一棵三叉树，其中兄弟节点包含的样本存在交集，交集中的样本起到诱导点的作用，可构建相邻区域的依赖关系.然后利用每个叶子结点所包含的样本建立局部的高斯过程回归模型，在当前假设下，每个父节点的边缘似然和预测分布可通过组合其子节点的计算结果来近似，从而降低计算量.同时，这种组合方式可保证拟合的函数是连续的.理论分析表明，对于n个训练样本，近似模型训练和预测的时间复杂度均为O(nt)，其中t与交集的大小相关，通常介于1与2之间.此外通过在公共数据集上的实验对比也验证了本文近似模型的有效性.
关键词: 模式识别 高斯过程 回归 贝叶斯学习 大规模机器学习
Overlapped Local Gaussian Process Regression
LIU Xiaofang2, LIU Ce1, LIU Lumi3, CHENG Dansong1
1. School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China;
2. School of Electrical Engineering & Automation, Harbin Institute of Technology, Harbin 150001, China;
3. Beijing Institute of Control Engineering, Beijing 100000, China
Abstract: Gaussian processes (GPs) are distributions of functions, and are commonly used for regression in machine learning community. For n training samples, their time complexity for training and prediction is O(n3) and O(n2) respectively. The high computational cost hinders their application to large datasets. Inspired by the divide and conquer strategy, the paper proposed a simple but efficient approximate model, called Overlapped Local Gaussian Process (OLGP). The method assumes that given the nearest neighbors, the random variables are independent of farther ones. The training samples are recursively divided and a ternary tree is constructed in the end. Sibling nodes have intersections where the samples play the role of inducing points to model the dependency between neighboring regions. Each leaf node is associated with a local GP regression model. The evidence and predictive distribution in parent nodes are composed of the ones from their sons, which reduces the computational cost significantly. Furthermore, the fitted function is guaranteed to be continuous. A theoretical analysis shows that the time complexity for training and prediction reduces to O(nt) for n training samples, where t depends on the proportion of the intersection in each level, and is usually between 1 and 2. The paper demonstrated the effectiveness of the method by speed-accuracy performance on several real-world datasets.
Keywords: pattern recognition gaussian process regression bayesian learning large scale machine learning
高斯过程(Gaussian Process, GP)[1]是机器学习领域常用的回归模型.在最近一段时间，GP已对许多研究领域产生了重要影响，比如地统计学[2]，优化[3]，降维[4]，强化学习[5]等.然而对于n个训练样本，GP回归的训练和预测时间复杂度分别为O(n3)和O(n2)，所以通常只能应用于一万左右规模的数据.为了克服计算代价的限制，许多学者提出了不同的近似方法，其中主流方法[6-9]是从冗余的训练数据中选取m个有代表性的样本，称为“诱导点”，并假设这些诱导点是训练数据的充分统计量.通常此类方法训练和预测时间复杂度分别为O(nm2)和O(m2)，在m?n的条件下可明显降低计算量，所以称为稀疏近似.但是在实际应用中，真实的函数往往比较复杂，少量诱导点难以充分代表训练数据集，导致拟合出的函数过于平滑.
针对这个问题，一些学者[10-15]提出了局部高斯过程.此类方法将样本空间划分成一系列局部区域，并近似区域之间的依赖关系，从而降低计算量.但是该类方法拟合的函数在区域的边界处可能会偏离原始函数或出现间断点.Snelson等[10]和Liu等[11]借助一定数目的全局诱导点来构建函数的整体趋势，以弥补近似模型在区域边界的缺陷，但计算复杂度会随诱导点数目的增加而急剧增加.Chen等[14]以及Lee等[15]对训练样本采用递归划分的方式，并在每一层都引入局部诱导点，一定程度上缓解了对全局诱导点的依赖.然而，每一层的诱导点由于时间复杂度过高，数量仍然受到严重限制，远远不能随着训练集规模的增加而线性增加.
针对以上问题，本文提出一种简单高效的近似模型来降低计算代价，称之为重叠局部高斯过程.对于n个训练样本，近似模型训练和预测的时间复杂度均为O(nt)，其中t与交集的大小相关，通常介于1与2之间.
1 高斯过程回归考虑一个数据集D，包含n个d维输入向量X ={xi}i=1n以及对应的n个一维目标值y={yi}i=1n.假设每个目标值是利用以d维向量x为输入的函数f(x)进行映射，然后被独立同分布的噪声干扰得到的，即目标值和输入的关系为
$y_{i}=f\left(\boldsymbol{x}_{i}\right)+\boldsymbol{\epsilon}_{i}.$ (1)
式中?i服从均值为0，标准差为σ的高斯分布.
假设函数f(x)服从均值函数恒为0, 协方差函数为k(x, x′)的高斯过程先验.
$f(\boldsymbol{x}) \sim G P\left(0, k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\right).$
则f(x)在X上的n个取值f=f(X)服从n维高斯分布
$p(\boldsymbol{f})=N\left(\boldsymbol{0}, \boldsymbol{K}_{\mathrm{X}}\right).$ (2)
式中KX=K(X, X).
结合先验分布式(2)和似然函数式(1)，可得f的后验分布.
$p(\mathit{\boldsymbol{f}}|\mathit{\boldsymbol{y}}) = N\left( {{\mathit{\boldsymbol{K}}_{\rm{X}}}\mathit{\boldsymbol{K}}_{\rm{y}}^{ - 1}\mathit{\boldsymbol{y}}, {\mathit{\boldsymbol{K}}_{\rm{X}}} - {\mathit{\boldsymbol{K}}_{\rm{X}}}\mathit{\boldsymbol{K}}_{\rm{y}}^{ - 1}{\mathit{\boldsymbol{K}}_{\rm{X}}}} \right).$
式中Ky=KX+σ2In.
输入x*处的目标值f*=f(x*)的预测分布为
$\begin{aligned} p(f_{*} | \boldsymbol{y})=& \int p\left(f_{*} | \boldsymbol{f}\right) p(\boldsymbol{f} | \boldsymbol{y}) \mathrm{d} \boldsymbol{f}=\\ & N\left(m_{*}, \boldsymbol{\sigma}_{*}^{2}\right). \end{aligned}$ (3)
可得：
$\begin{array}{c}{m_{*}=\boldsymbol{k}_{* X} \boldsymbol{K}_{\mathrm{y}}^{-1} \boldsymbol{y}}, \\ {\boldsymbol{\sigma}_{*}^{2}=k_{*}-\boldsymbol{k}_{* X} \boldsymbol{K}_{\mathrm{y}}^{-1} \boldsymbol{k}_{X *}}, \end{array}$
式中: k*X=K(x*, X)，kX*=K(X, x*).
训练时，将核函数中的超参数，以及噪声分布的超参数σ一起记为向量θ，通过梯度下降法最大化对数似然.
$\log p(\boldsymbol{y})=\log \int p(\boldsymbol{y} | \boldsymbol{f})_{p}(\boldsymbol{f}) \mathrm{d} f=\log N\left(\boldsymbol{0}, \boldsymbol{K}_{{\rm y}}\right).$ (4)
来训练超参数θ的值.
然而，在利用式(3)计算预测分布，以及利用式(4)训练超参数的时候，都需要计算协方差矩阵Ky的逆，时间代价为O(n3).
2 重叠局部高斯过程回归随机变量在给定邻近变量的值后，会与距离较远的变量条件独立.如图 1所示，其中蓝色加号和紫色圆点均代表训练样本，蓝色实线和虚线是用蓝色样本得到的预测分布，其中实线描述预测均值，虚线描述预测分布的标准差.而灰色区域是用紫色和蓝色的训练样本一起得到的预测分布.两种方式得到的预测分布几乎重合，说明在给定蓝色样本的观测值后，垂直的绿色虚线右方的函数值，与紫色样本的观测值相关性比较小.
Fig. 1
图 1 马尔科夫假设 Fig. 1 Markov Assumption 将所有训练样本投影到一个法向量上，根据投影将数据划分为3部分.中间的部分为(X3, y3)，其余两部分分别为(X1, y1)和(X2, y2)，并假设y1和y2在给定y3的情况下条件独立.
2.1 近似模型似然和预测分布在当前假设下，y的分布近似为
$p(\boldsymbol{y}) \approx q(\boldsymbol{y})=\frac{p\left(\boldsymbol{y}_{1}, \boldsymbol{y}_{3}\right) p\left(\boldsymbol{y}_{2}, \boldsymbol{y}_{3}\right)}{p\left(\boldsymbol{y}_{3}\right)}.$
式中:p(y1, y3)，p(y2, y3)以及p(y3)均为原联合高斯分布p(y)的边缘分布.q(y)仍然为高斯分布.
$q(\boldsymbol{y})=N\left(\bf{0}, \widetilde{\boldsymbol{K}}_{{\rm y}}\right)$
式中
$\widetilde{\boldsymbol{K}}_{\mathrm{y}}=\left[\begin{array}{ccc}{\boldsymbol{K}_{1}} & {\boldsymbol{Q}} & {\boldsymbol{K}_{13}} \\ {\boldsymbol{Q}^{\mathrm{T}}} & {\boldsymbol{K}_{2}} & {\boldsymbol{K}_{23}} \\ {\boldsymbol{K}_{31}} & {\boldsymbol{K}_{32}} & {\boldsymbol{K}_{3}}\end{array}\right].$
式中：Ki=K(Xi, Xi)+σ2I，Kij=K(Xi, Xj)，Q=K13K3-1K32，
然而对于训练来说，不需要显式计算
$\log q(\boldsymbol{y})=\log p\left(\boldsymbol{y}_{1}, \boldsymbol{y}_{3}\right)+\log p\left(\boldsymbol{y}_{2}, \boldsymbol{y}_{3}\right)-\log p\left(\boldsymbol{y}_{3}\right)$
来训练超参数θ.这样相当于将原始数据划分为三部分，因为y3可看作y3∪y1和y3∪y2的交集，所以这个方法称为重叠局部高斯过程.y3，y3∪y1以及y3∪y2均可按同样方式递归分解，从而降低计算量.构建的三叉树如图 2(a)所示.
Fig. 2
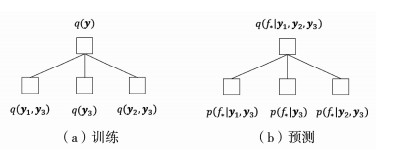图 2 三叉树 Fig. 2 Ternary Tree 对于输入x*处目标值f*=f(x*)的预测分布，假设y1和y2在给定y3以及f*的条件下独立，可得
$q\left(f_* | \boldsymbol{y}_{1}, \boldsymbol{y}_{2}, \boldsymbol{y}_{3}\right)=\frac{p\left(f_* | \boldsymbol{y}_{1}, \boldsymbol{y}_{3}\right) p\left(f_* | \boldsymbol{y}_{2}, \boldsymbol{y}_{3}\right)}{p\left(f_* | \boldsymbol{y}_{3}\right)}.$
式中:等号右侧每一项p(f*|.)为利用局部数据得到的预测分布.在合并p(f*|.)时，多个高斯概率密度乘除运算结果仍为高斯概率密度形式，所以q(f*|.y1, y2, y3)仍为高斯分布，并且可计算均值和协方差的解析解[13]，这里不再赘述.因为分式中每一项p(f*|.)都是连续的，所以q(f*|.y1, y2, y3)也是连续的.构建的三叉树如图 2(b)所示.
2.2 递归划分算法算法1??对训练数据(X, y)递归划分，构建一棵三叉树.算法首先随机抽取小部分训练样本的特征
算法1??递归划分算法
Input:
Trainingdata (X, y); Projection Threshold α; Iteration Threshold β; Sampling Number m;
Output:
Ternary Tree T;
FunctionConstructTree((X, y), α, β, m):
1. If Size((X, y)) < β
2. T.data←(X, y)
3. Else
4. Randomly sample m samples
5. Perform K-Means on
6.
7.(X1, y1), (X2, y2), (X3, y3) ←?
8. For each (x, y)∈(X, y) do
9. If n·x < -α(X1, y1)←(X1, y1)∪(x, y)
10. Else if n·x >α(X2, y2)←(X2, y2)∪(x, y)
11. Else (X3, y3)←(X3, y3)∪(x, y)
12. T.left←ConstructTree((X1, y1)∪(X3, y3), α, β, m)
13. T.right←ConstructTree((X2, y2)∪(X3, y3), α, β, m)
14. T.middle←ConstructTree((X3, y3), α, β, m)
15. Return T
首先在小部分训练样本上通过最大化准确的边缘似然来初始化核函数的超参数，然后用初始超参数归一化训练集后再进行划分.划分的时间复杂度是O(nlog(n))，通常会重复多次，选择计算代价最小的一次.之后就固定下来，不再重新划分.
2.3 时间复杂度分析模型的计算时间复杂度和划分结果是紧密相关的.一次划分之后，需要针对(X3, y3)，(X3, y3)∪(X1, y1)以及(X3, y3)∪(X2, y2)分别训练局部高斯过程模型.假设ni是(Xi, yi)的大小，那么训练时间复杂度变为O((n1+n3)3+(n2+n3)3+n33).
如果递归对(X3, y3)，(X3, y3)∪(X1, y1)以及(X3, y3)∪(X2, y2)进行分解，可进一步降低时间复杂度.整体的运行时间会与递归的深度，每层中n3的大小紧密相关.为了便于分析，假设对于每一层n1≈n2，n3≈2γn，2γ为诱导点的比例.可得关于T(n)的递推式.
$T(n)=\left\{\begin{array}{l}{O\left(n^{3}\right) n<\beta, } \\ {2 T\left(\frac{n}{2}+\gamma n\right)+T(2 \gamma n)+O(n) \text { otherwise }}.\end{array}\right.$
在
$T(n)=\theta\left(n^{t}\right).$
式中t为下式的解
$2\left(\frac{1}{2}+\gamma\right)^{t}+(2 \gamma)^{t}=1.$
t关于γ的变化曲线如图 3所示.当t=2时，γ=1/6，表示每层诱导点的比例为2γ=1/3.因此算法在θ(n2)的时间复杂度下，可让每层诱导点数目达到1/3比例.
Fig. 3
图 3 t关于γ的变化曲线 Fig. 3 t as a function of γ 3 实验分析本节在真实数据集上分析超参数α和β对模型性能的影响，并在Chalupka等[17]提出的框架下与其他模型进行对比.对于本节的所有实验，所有模型均使用Matern-3/2核[1]，每个特征有独立的缩放参数，并采用高斯似然函数.在每轮实验中，所有模型均用同一组超参数初始化.这组超参数是在随机抽取的1 000个训练样本上通过最大化准确的边缘似然训练得到的.之后本文的模型OLGP使用共轭梯度法在整个训练集上继续优化超参数，其实现借助了GPML工具箱[18].而其他模型采用开源代码里的默认方法来优化.训练时间包括优化核函数超参数和诱导点参数的时间.本文采用评价标准MSLL(the Mean Standardized Log Loss)量化模型预测效果.实验所有结果都是重复5遍取平均值得到的.
3.1 超参数的影响在Pole Telecomm数据集[19]上测试了OLGP在不同超参数下的性能.Pole数据集有10 000个训练样本和5 000个测试样本.本文采用Lázaro-Gredilla等[20]的方法对数据预处理，保留其中26维特征，实验结果如图 4所示.
Fig. 4
图 4 超参数影响 Fig. 4 The influence of hyperparameters 图中每种颜色或形状的4个标记从左到右α值分别为0.0，0.04，0.07，0.1.不同颜色或形状的标记代表不同的β值.如图所示，β参数越小，训练及测试的误差越大，说明每次分解都会引入一定误差.同时，训练及测试所需时间变短，说明分解可降低计算代价.对于相同的β值，α值越小，方法训练和测试误差越大，说明减少每一层诱导点的数目会增大误差.但训练和测试的时间均变短，说明减少诱导点数目可降低计算代价.
当β≥1 000且α≥0.04时，增加β或α的值，训练和测试误差的变化幅度较小，但会明显增加训练或测试的时间.通常固定β=1 000，并根据实际情况调整α的值.
3.2 模型比较在两个真实数据集上测试近似模型的性能，并和最近提出的两个模型grBCM[11], VFF[21]进行比较.
在Pole数据集[19]上的实验结果如图 5(a)和(b)所示.首先，VFF属于稀疏近似方法，难以在相近的时间内达到合理的精度.OLGP中固定β=1 000，4个圆圈从左到右α值分别为0.0，0.04，0.07，0.1.图 5(b)显示OLGP和grBCM测试精度相近，但是OLGP所用时间只有grBCM的一半.因为在OLGP中，诱导点可递归分解，所以相比于grBCM，OLGP可用更低的计算代价，达到相近的精度.然而，图 5(a)中OLGP所用训练时间略大于grBCM，这是因为Liu等[12]提供的grBCM工具包在训练时，没有耦合全局诱导点和局部样本.这种训练方式可能导致学习到的超参数有更大的偏差.
Fig. 5
图 5 模型对比 Fig. 5 Model comparison Sarcos数据集[22]有21维特征，44 484个训练样本和4 449个测试样本，实验结果如图 5(c)和(d)所示.同样，VFF方法很难达到grBCM和OLGP两种方法的性能.OLGP方法中β=1 000，4个圆圈从左到右α值分别为0.0，0.002，0.005，0.008.在Sarcos数据集上的实验结论与Pole数据集上相同.
4 结论针对高斯过程回归训练时间复杂度过高的问题，本文基于分治思想提出了重叠局部高斯过程模型，并通过理论分析和实验证明了模型在保持一定精度的前提下，可显著降低训练时间复杂度.未来的工作中，将对诱导点尝试更有效地采样方式，以进一步提升近似效果.
参考文献
[1] WILLIAMS C K I, RASMUSSEN C E. Gaussian processes for machine learning[M]. Cambridge, MA: MIT Press, 2006: 7.
[2] CRESSIE N. Statistics for spatial data[J]. Terra Nova, 1992, 4(5): 613. DOI:10.1002/9781119115151
[3] JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455. DOI:10.1023/A:1008306431147
[4] LAWRENCE N. Probabilistic non-linear principal component analysis with Gaussian process latent variable models[J]. Journal of Machine Learning Research, 2005, 6(Nov): 1783.
[5] DEISENROTH M P, FOX D, RASMUSSEN C E. Gaussian processes for data-efficient learning in robotics and control[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 37(2): 408. DOI:10.1109/tpami.2013.218
[6] BUI T D, YAN J, TURNER R E. A unifying framework for Gaussian process pseudo-point approximations using power expectation propagation[J]. Journal of Machine Learning Research, 2017, 18(1): 3649.
[7] TITSIAS M. Variational learning of inducing variables in sparse Gaussian processes[C]//VAN DYK D, WELLING M. Artificial Intelligence and Statistics. Cambridge, MA: JMLR, 2009: 567
[8] SNELSON E, GHAHRAMANI Z. Sparse Gaussian processes using pseudo-inputs[C]//International Confereiue on Neural Information Systems MIT Press, 2005
[9] QUI?ONERO-CANDELA J, RASMUSSEN C E. A unifying view of sparse approximate Gaussian process regression[J]. Journal of Machine Learning Research, 2005, 6(Dec): 1939.
[10] SNELSON E, GHAHRAMANI Z. Local and global sparse Gaussian process approximations[C]//Artificial Intelligence and Statistics. Cambridge, MA: JMLR, 2007: 524
[11] LIU Haitao, CAI Jianfei, WANG Yi, et al. Generalized Robust Bayesian Committee Machine for Large-scale Gaussian Process Regression[C]//International Conference on Machine Learning. New York, NY: ACM, 2018: 3137
[12] TRESP V. A Bayesian committee machine[J]. Neural Computation, 2000, 12(11): 2719. DOI:10.1162/089976600300014908
[13] BUI T D, TURNER R E. Tree-structured Gaussian process approximations[C]//Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2014: 2213
[14] CHEN Jie, AVRON H, SINDHWANI V. Hierarchically compositional kernels for scalable nonparametric learning[J]. Journal of Machine Learning Research, 2017, 18(1): 2214.
[15] LEE B J, LEE J, KIM K E. Hierarchically-partitioned Gaussian process approximation[C]//Artificial Intelligence and Statistics. Cambridge, MA: JMLR, 2017: 822
[16] AKRA M, BAZZI L. On the solution of linear recurrence equations[J]. Computational Optimization and Applications, 1998, 10(2): 195. DOI:10.1023/A:1018373005182
[17] CHALUPKA K, WILLIAMS C K I, MURRAY I. A framework for evaluating approximation methods for Gaussian process regression[J]. Journal of Machine Learning Research, 2013, 14(Feb): 333.
[18] RASMUSSEN C E, HANNES N. Gaussian processes for machine learning (GPML) toolbox[J]. Journal of Machine Learning Research, 2010, 11(Nov): 3011.
[19] LUIS T. Regression Data Sets[DB/OL].[2019-06-17]. https://www.dcc.fc.up.pt/~ltorgo/Regression/DataSets.html
[20] LAZARO-GREDILLA M, QUINONERO-CANDELA J, RASMUSSEN C E, et al. Sparse Spectrum Gaussian Process Regression[J]. Journal of Machine Learning Research, 2010, 11(Jun): 1865.
[21] HENSMAN J, DURRANDE N, SOLIN A. Variational Fourier Features for Gaussian Processes[J]. Journal of Machine Learning Research, 2018, 18(151): 1.
[22] RASMUSSEN C E. Data[DB/OL].[2019-06-17]. http://www.gaussianprocess.org/gpml/data/
