马春阳,宋功发,赵军明,刘林华
(哈尔滨工业大学 能源科学与工程学院, 哈尔滨 150001)
摘要:
为提高微藻光生物反应器的效率以降低成本及进行规模化培养，提出一种在线测量微藻细胞全生长期辐射特性的方法.采用定制的平板式光生物反应器，给出一种微藻生长期辐射特性在线测量方案，分析传统测量方法应用于生长期微藻辐射特性测量的局限性，基于微藻细胞辐射特性的特征提出改进方案，并以普通小球藻为例进行生长期辐射特性的实验研究.结果表明，提出的辐射特性在线测量方案可以有效地应用于微藻时间相关辐射特性的测量，改进的光谱吸收系数及衰减系数测量方法可以更准确地应用于生长过程中细胞浓度变化时辐射特性的测量，普通小球藻的可见光波段光谱吸收截面和光谱衰减截面随时间变化显著.本研究为微藻生长期辐射特性的测量提供了一种方便可行的实验方案.
关键词: 时间依赖辐射特性 微藻 小球藻 光生物反应器 实验测量方法
DOI：10.11918/j.issn.0367-6234.201707121
分类号:TK121；Q819
文献标识码:A
基金项目:国家自然科学基金(1,3)
Experimental method of the radiative properties of microalgae at different growth period
MA Chunyang,SONG Gongfa,ZHAO Junming,LIU Linhua
(School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract:
To improve the efficiency of microalgae photobioreactor to reduce cultivation costs and carry out large-scale cultivation, an online measurement method was proposed to measure the radiative properties of microalgae at whole growth phase. Using a custom flate-plate photobioreactor, an online measurement scheme for the radiative properties of microalgae was presented and the limitation of traditional measurement method was studied. An improved scheme was proposed based on the characteristics of radiative properties of microalgae. Chlorella vulgaris was taken as an example and its radiative properties at growth phase was experimentally studied. The results show that the proposed online measurement scheme can be effectively applied to measure the time-dependent radiative properties of microalgae. The improved scheme of spectral absorption and extinction coefficient measurement are more accurately applied to measure the radiative properties of microalgae at different growth phase with varied cell concentration. The spectral absorption and extinction corss-sections of Chlorella vulgaris vary significantly with growth time in the visible spectral range. This work provides a convenient and feasible experimental scheme for the measurement of radiative properties of microalgae at different growth period.
Key words: time-dependent radiative properties microalgae Chlorella photobioreactor experimental methods
马春阳, 宋功发, 赵军明, 刘林华. 微藻生长期辐射特性测量方法[J]. 哈尔滨工业大学学报, 2018, 50(1): 50-58. DOI: 10.11918/j.issn.0367-6234.201707121.
MA Chunyang, SONG Gongfa, ZHAO Junming, LIU Linhua. Experimental method of the radiative properties of microalgae at different growth period[J]. Journal of Harbin Institute of Technology, 2018, 50(1): 50-58. DOI: 10.11918/j.issn.0367-6234.201707121.
基金项目 国家自然科学基金(51276051, 51421063) 作者简介 马春阳(1990—)，男，博士研究生;
赵军明(1980—)，男，教授，博士生导师;
刘林华(1966—)，男，****特聘教授，博士生导师 通信作者 赵军明，jmzhao@hit.edu.cn 文章历史 收稿日期: 2017-07-17
Contents -->Abstract Full text Figures/Tables PDF
微藻生长期辐射特性测量方法
马春阳, 宋功发, 赵军明
, 刘林华 哈尔滨工业大学 能源科学与工程学院，哈尔滨 150001
收稿日期: 2017-07-17
基金项目: 国家自然科学基金(51276051, 51421063)
作者简介: 马春阳(1990—)，男，博士研究生;
赵军明(1980—)，男，教授，博士生导师;
刘林华(1966—)，男，****特聘教授，博士生导师
通信作者: 赵军明，jmzhao@hit.edu.cn
摘要: 为提高微藻光生物反应器的效率以降低成本及进行规模化培养，提出一种在线测量微藻细胞全生长期辐射特性的方法.采用定制的平板式光生物反应器，给出一种微藻生长期辐射特性在线测量方案，分析传统测量方法应用于生长期微藻辐射特性测量的局限性，基于微藻细胞辐射特性的特征提出改进方案，并以普通小球藻为例进行生长期辐射特性的实验研究.结果表明，提出的辐射特性在线测量方案可以有效地应用于微藻时间相关辐射特性的测量，改进的光谱吸收系数及衰减系数测量方法可以更准确地应用于生长过程中细胞浓度变化时辐射特性的测量，普通小球藻的可见光波段光谱吸收截面和光谱衰减截面随时间变化显著.本研究为微藻生长期辐射特性的测量提供了一种方便可行的实验方案.
关键词: 时间依赖辐射特性 微藻 小球藻 光生物反应器 实验测量方法
Experimental method of the radiative properties of microalgae at different growth period
MA Chunyang, SONG Gongfa, ZHAO Junming
, LIU Linhua School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
Abstract: To improve the efficiency of microalgae photobioreactor to reduce cultivation costs and carry out large-scale cultivation, an online measurement method was proposed to measure the radiative properties of microalgae at whole growth phase. Using a custom flate-plate photobioreactor, an online measurement scheme for the radiative properties of microalgae was presented and the limitation of traditional measurement method was studied. An improved scheme was proposed based on the characteristics of radiative properties of microalgae. Chlorella vulgaris was taken as an example and its radiative properties at growth phase was experimentally studied. The results show that the proposed online measurement scheme can be effectively applied to measure the time-dependent radiative properties of microalgae. The improved scheme of spectral absorption and extinction coefficient measurement are more accurately applied to measure the radiative properties of microalgae at different growth phase with varied cell concentration. The spectral absorption and extinction corss-sections of Chlorella vulgaris vary significantly with growth time in the visible spectral range. This work provides a convenient and feasible experimental scheme for the measurement of radiative properties of microalgae at different growth period.
Key words: time-dependent radiative properties microalgae Chlorella photobioreactor experimental methods
化石燃料的大量使用导致温室气体的大量排放，进而恶化全球的气候环境[1].微藻作为一种绿色生物质能源，相比于陆生植物具有生长迅速、光合效率高且不占用耕地等优点[2].微藻可以积累油脂用于生产生物柴油，部分微藻可以产生氢气，微藻亦可作为保健食品[3-6].另一方面，微藻的大量培养可固定由于化石燃料大量使用而释放的CO2温室气体[7].因而微藻被认为是非常有前景的未来可持续发展的绿色生物质能源[8].
尽管微藻作为生物质能源具有很多优点，但目前其培养成本较高，如何降低其培养成本提高微藻产量是目前面对的关键问题.影响微藻生长的因素较多，主要有光照、温度、营养物质以及pH值等[9-10].其中光能在微藻混悬液中的分布是影响微藻生长效率的一个重要因素[11].研究表明，微藻的生长需要适宜的光照强度，过高或过低的光照强度都会降低微藻的生长速度[12-14].因此分析及优化光生物反应器内的光强分布对于提高微藻的生长效率至关重要.
限于实验条件及实验难度，目前, 国际上已开展的微藻辐射特性的研究主要是对处于生长稳定期的微藻细胞的测量.然而，由于微藻细胞的生长，微藻辐射特性必然随着生长过程发生变化，最近的研究结果也表明了这一点[15].传统的稳定期的辐射特性测量基于单散射假设，而对于处于生长期的微藻则不能对其进行稀释以满足单散射条件，只能对其进行在线测量，需要提出新的测量方法以及对传统测量方法应用于在线测量时的误差进行分析.研究表明，微藻混悬液的散射相函数在生长期间基本不变[15].因此，光谱衰减系数和吸收系数是研究生长期辐射特性的两个关键辐射特性参数.
本文给出了一种微藻生长期辐射特性在线测量方案，分析了传统测量方法应用于生长期微藻辐射特性测量的局限性，基于微藻细胞辐射特性的特征提出了改进方案，最后以普通小球藻为例进行了生长期辐射特性的实验研究.
1 微藻辐射特性在线实验测量图 1给出了光生物反应器中的光传输过程示意图.微藻混悬液可以等效为半透明的吸收散射性介质，其中的辐射传输过程可由辐射传递方程来定量描述[16].
$\begin{array}{l}\mathit{\boldsymbol{s}} \cdot \nabla {I_\lambda }\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) = - {\beta _\lambda }{I_\lambda }\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}\int_{\mathit{\Omega '} = 4{\rm{ \mathsf{ π} }}} {{I_\lambda }\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s'}}} \right){\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}} \to \mathit{\boldsymbol{s}}} \right){\rm{d}}\mathit{\Omega '}} .\end{array}$ (1)
Figure 1
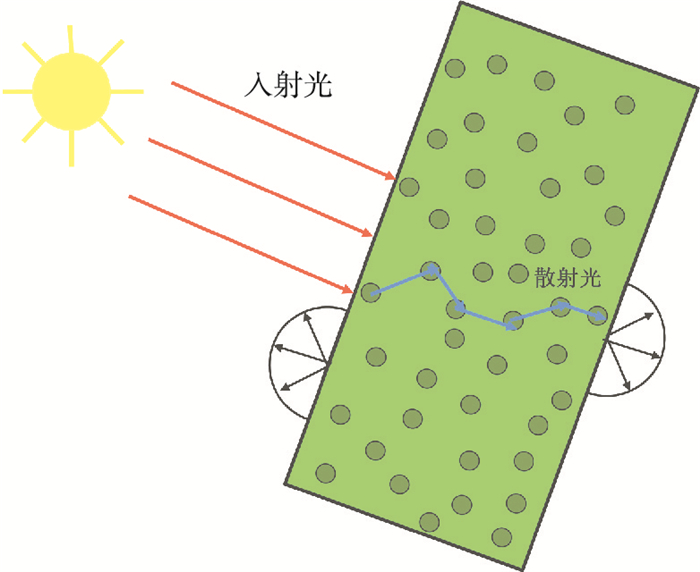图 1 光生物反应器中光传输示意 Figure 1 The schematic of light transfer in photobioreactor 式中：Iλ表示光谱辐射强度；βλ=κa, λ+κs, λ表示微藻混悬液的光谱衰减系数，κs, λ表示光谱散射系数，κa, λ表示光谱吸收系数；Ω′表示立体角；散射相函数Φλ(s′, s)表示s′方向的辐射散射进入s方向的概率，散射相函数满足归一化条件[16]
$\frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_{4{\rm{ \mathsf{ π} }}} {{\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}},\mathit{\boldsymbol{s}}} \right){\rm{d}}\mathit{\Omega }} = 1;$
不对称因子gλ的定义如下[15]：
${g_\lambda } = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_{4{\rm{ \mathsf{ π} }}} {{\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}},\mathit{\boldsymbol{s}}} \right){\rm{cos}}\theta {\rm{d}}\mathit{\Omega }} .$
实验研究表明，微藻混悬液是一种具有强前向散射特性的介质，其不对称因子gλ约为0.97~0.98[17-20]，同时，Henyey-Greenstein散射相函数可作为微藻散射相函数的一个很好的近似.光谱吸收和衰减系数可以分别使用光谱吸收和衰减截面表达[16]：
${\kappa _{{\rm{a}},\lambda }} = {C_{{\rm{abs,}}\lambda }}N,$
${\beta _\lambda } = {C_{{\rm{ext,}}\lambda }}N.$
式中:Cabs, λ和Cext, λ分别表示光谱吸收和衰减截面，N表示微藻数密度(单位：m-3).从辐射传递方程可以看出，微藻辐射特性是求解辐射传递方程的基础参数.
目前, 微藻辐射特性的研究主要集中于生长稳定期[17, 19-20]，其实验测量过程仅对生长稳定期进行取样，因而实验测量难度较小.但由于微藻细胞的生长和代谢过程中，其辐射特性是随生长发生变化的.为了对微藻整个生长期辐射特性进行在线测量，本文设计了一种定制的将微藻培养与辐射特性测量集成为一体的光生物反应器，给出了一种微藻生长期辐射特性在线测量方案.本文提出了一种辐射特性在线测量的一般方法，对于实际的光生物反应器可以采用取样的方式放入平板式光生物反应器进行测量.定制的光生物反应器如图 2所示，该反应器的几何结构可以近似满足在法向光照下维持一维辐射传输条件，因而可以方便实现微藻生长期辐射特性的在线测量. 图 2(a)为定制光生物反应器实物图(厚度为10 mm)，由石英玻璃制成.石英玻璃在可见光波段具有很高的透过率，可以很好地满足所研究的微藻辐射特性的波长范围. 图 2(b)为辐射特性测量光路布置示意图，由于比色皿的厚度远小于其长宽，所以光源通过光生物反应器的过程可以近似为一维问题，可以直接放置在实验系统中进行辐射特性测量.培养及测量过程中始终保持光生物反应器封闭，以保证培养过程中及辐射特性测量时不被杂菌污染.
Figure 2
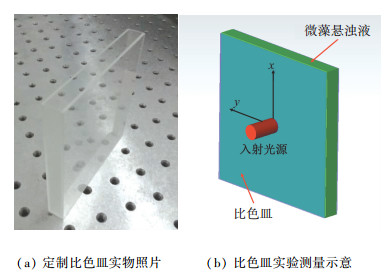图 2 光生物反应器 Figure 2 Photobioreactor 2 微藻辐射特性传统测量方法光谱吸收系数、光谱散射系数及散射相函数是求解辐射传递方程的基本物性参数.实际测量中，可以使用积分球测量吸收系数，使用法向透过率信号获得衰减系数，而散射相函数可以使用散射测量仪进行测量.下面给出微藻光谱吸收系数及衰减系数实验测量的传统测量方法的原理及测量误差的分析.
2.1 光谱吸收系数测量如前所述，微藻是一种具有强前向散射特性的介质，因此可以通过测量半球透过率来获得微藻的吸收系数.下面给出吸收系数测量的测量原理.对辐射传递方程(1)作角度空间积分可得无发射介质的辐射能量方程为[15]
$\nabla \cdot {\mathit{\boldsymbol{q}}_\lambda } = - {\kappa _{{\rm{a}},\lambda }}{G_\lambda }.$ (2)
其中，
$\frac{{{\rm{d}}{q_{\lambda ,x}}}}{{{\rm{d}}x}} = - {\kappa _{{\rm{a}},\lambda }}{G_\lambda }.$ (3)
同时投射辐射也只是x坐标的函数,
$\begin{array}{*{20}{c}}{{q_{\lambda ,x}}\left( x \right) = \int\limits_{4{\rm{ \mathsf{ π} }}} {\cos \theta {I_\lambda }\left( {x,\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)\sin \theta {\rm{d}}\theta {\rm{d}}\varphi } = }\\{2{\rm{ \mathsf{ π} }}\int\limits_{ - 1}^1 {\xi {I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } ,}\end{array}$
${G_\lambda }\left( x \right) = \int\limits_{4{\rm{ \mathsf{ π} }}} {{I_\lambda }\left( {x,\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)\sin \theta {\rm{d}}\theta {\rm{d}}\varphi } = 2{\rm{ \mathsf{ π} }}\int\limits_{ - 1}^1 {{I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } .$
假设散射相函数具有强前向散射特征，因此，辐射强度仅在前向很小的角度范围内才具有显著的数值，ξ∈[-δ, δ]，δ为一很小数值.假设相对于辐射强度，ξ在该小角度区间内为缓变量，此时热流可以表示为
$\begin{array}{l}{q_{\lambda ,x}}\left( x \right) = 2{\rm{ \mathsf{ π} }}\int\limits_{ - 1}^1 {\xi {I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } \doteq 2{\rm{ \mathsf{ π} }}{\xi _0}\int\limits_{ - \delta }^\delta {{I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } = \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;2{\rm{ \mathsf{ π} }}\int\limits_{ - \delta }^\delta {{I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } .\end{array}$
式中ξ0取角度区间中心的值，ξ0=1.由上面的假设，Gλ(x)可以表示为
${G_\lambda }\left( x \right) = 2{\rm{ \mathsf{ π} }}\int\limits_{ - 1}^1 {{I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } \doteq 2{\rm{ \mathsf{ π} }}\int\limits_{ - \delta }^\delta {{I_\lambda }\left( {x,\xi } \right){\rm{d}}\xi } ,$
从而qλ, x(x)=Gλ(x)，因而式(3)可以写为
$\frac{{{\rm{d}}{q_{\lambda ,x}}}}{{{\rm{d}}x}} = - {\kappa _{{\rm{a}},\lambda }}{q_{\lambda ,x}},$
即辐射热流满足如下形式的关系式：
${q_{\lambda ,x}}\left( x \right) = {q_{\lambda ,x}}\left( 0 \right){{\rm{e}}^{ - {\kappa _{{\rm{a}},\lambda }}x}}.$ (4)
根据比尔定律可知，无散射介质的辐射热流准确满足式(4).热流的透过率为
${q_{\lambda ,x}}\left( L \right)/{q_{\lambda ,x}}\left( 0 \right) = {{\rm{e}}^{ - {\kappa _{{\rm{a}},\lambda }}L}}.$
对于微藻混悬液，总的吸收系数为液体介质吸收与藻细胞吸收之和.
图 3给出了吸收系数测量示意图及实验装置照片，实验用光谱仪可以测量波长范围200~1 100 nm的透过率数据，实验测量时需要将被测样品置于比色皿中.实验测量过程为1)测量比色皿加培养基时测得的光谱强度，参考信号Th, λ, ref；2)测量比色皿加微藻混悬液的光谱强度，实验信号Th, λ.选取参考溶液置入比色皿，则总的半球透过率可以表示为
${T_{{\rm{h}},\lambda ,{\rm{ref}}}} = {T_{g,\lambda }}{{\rm{e}}^{ - {\kappa _{{\rm{a}},\lambda ,{\rm{liquid}}}}L}}{T_{g,\lambda }}.$
Figure 3
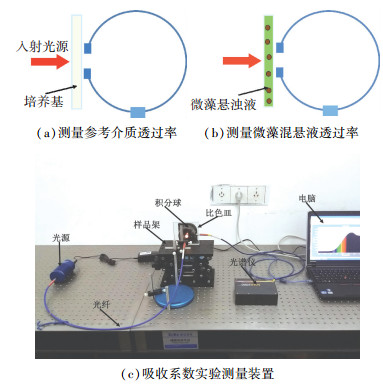图 3 吸收系数测量示意图及实验测量装置 Figure 3 The schematic of absorption coefficient measurement and photo of experimental setup 其中Tg, λ为定制光生物反应器玻璃板的光谱透过率，κa, λ, liquid表示培养基的光谱吸收系数.微藻混悬液的半球透过率可以表示为
${T_{{\rm{h}},\lambda }} = {T_{g,\lambda }}{{\rm{e}}^{ - \left( {{\kappa _{{\rm{a}},\lambda }} + {\kappa _{{\rm{a}},\lambda ,{\rm{liquid}}}}L} \right)}}{T_{g,\lambda }}.$
从而得到传统的普遍使用的吸收系数的表达式[20]:
${\kappa _{{\rm{a}},\lambda }} = - \frac{1}{L}\ln \left( {\frac{{{T_{{\rm{h}},\lambda }}}}{{{T_{{\rm{h}},\lambda ,{\rm{ref}}}}}}} \right).$ (5)
式中Th, λ和Th, λ, ref分别表示微藻混悬液的法向半球透过率和参考介质(培养基)的法向半球透过率，L表示微藻混悬液的几何厚度，下标λ表示波长.
根据以上推导过程，可知该测量方法要求被测介质的散射相函数必须具有强前向散射特征，同时忽略了两层玻璃盖板之间的多次反射作用.随着光生物反应器内细胞浓度的增加，盖板之间的多次反射作用会发生变化，这会引起测量结果的不确定性.石英玻璃比色皿是否适用于生长期光谱吸收特性的测量需要进行评估.
2.2 光谱衰减系数测量图 4给出了衰减系数测量光路布置示意图及实验装置照片.光谱仪可以测量波长范围200~1 100 nm的法向透过率数据，测量时将被测样品置于比色皿中.实验中分两组进行测量：1)比色皿内加入培养基测得的参考光谱辐射信号Tn, λ, ref；2)比色皿加入微藻混悬液测得的光谱强度Tn, λ.
Figure 4
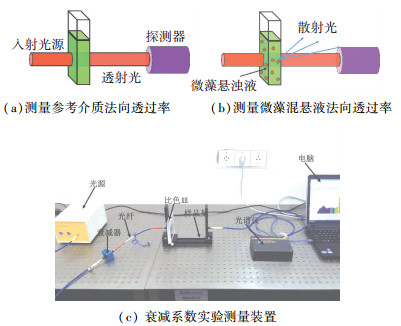图 4 衰减系数测量示意图及实验测量装置 Figure 4 The schematic of attenuation coefficient measurement and photo of experimental setup 辐射传递方程中的辐射强度可以分解为直射分量Iλ, c和漫射分量Iλ, d:
${I_\lambda }\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) = {I_{\lambda ,{\rm{c}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) + {I_{\lambda ,{\rm{d}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right),$
两个分量分别满足如下辐射传递方程:
$\mathit{\boldsymbol{s}} \cdot \nabla {I_{\lambda ,{\rm{c}}}} + {\beta _\lambda }{I_{\lambda ,{\rm{c}}}} = 0,$ (6)
$\begin{array}{l}\mathit{\boldsymbol{s}} \cdot \nabla {I_{\lambda ,{\rm{d}}}} + \beta {I_{\lambda ,{\rm{d}}}} = \frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}\int {{I_{\lambda ,{\rm{d}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s'}}} \right){\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}} \to \mathit{\boldsymbol{s}}} \right){\rm{d}}\mathit{\Omega '}} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}\int {{I_{\lambda ,{\rm{c}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s'}}} \right){\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}} \to \mathit{\boldsymbol{s}}} \right){\rm{d}}\mathit{\Omega '}} .\end{array}$ (7)
假设平行光照射方向为sc，则对于平行光分量其辐射强度可以写为
${I_{\lambda ,{\rm{c}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) = {q_{\lambda ,{\rm{c}}}}\left( \mathit{\boldsymbol{r}} \right)\delta \left( {\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}_{\rm{c}}}} \right).$
从而式(6)和(7)可以改写为
${\mathit{\boldsymbol{s}}_{\rm{c}}} \cdot \nabla {q_{\lambda ,{\rm{c}}}} + {\beta _\lambda }{q_{\lambda ,{\rm{c}}}} = 0,$ (8)
$\begin{array}{l}\mathit{\boldsymbol{s}} \cdot \nabla {I_{\lambda ,{\rm{d}}}} + {\beta _\lambda }{I_{\lambda ,{\rm{d}}}} = \frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}\int {{I_{\lambda ,{\rm{d}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s'}}} \right){\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}} \to \mathit{\boldsymbol{s}}} \right){\rm{d}}\mathit{\Omega '}} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}{q_{\lambda ,{\rm{c}}}}\left( \mathit{\boldsymbol{r}} \right){\mathit{\Phi }_\lambda }\left( {{{\mathit{\boldsymbol{s'}}}_{\rm{c}}} \to \mathit{\boldsymbol{s}}} \right).\end{array}$ (9)
下面分析漫射分量在平行光方向的数值，对式(9)取s=sc，可得
$\begin{array}{l}\mathit{\boldsymbol{s}} \cdot \nabla {I_{\lambda ,{\rm{d}}}} + {\beta _\lambda }{I_{\lambda ,{\rm{d}}}} = \frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}\int {{I_{\lambda ,{\rm{d}}}}\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s'}}} \right){\mathit{\Phi }_\lambda }\left( {\mathit{\boldsymbol{s'}} \to {\mathit{\boldsymbol{s}}_{\rm{c}}}} \right){\rm{d}}\mathit{\Omega '}} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\kappa _{{\rm{s}},\lambda }}}}{{4{\rm{ \mathsf{ π} }}}}{q_{\lambda ,{\rm{c}}}}\left( \mathit{\boldsymbol{r}} \right){\mathit{\Phi }_\lambda }\left( {{{\mathit{\boldsymbol{s'}}}_{\rm{c}}} \to {\mathit{\boldsymbol{s}}_{\rm{c}}}} \right).\end{array}$
可以看出，由于源项κs, λqλ, c(r)Φλ(sc→sc)/4π为非δ函数形式，Iλ, d也为非δ函数形式.从而在平行光方向，Iλ, d相对于Iλ, c可以忽略.只要探测器探测的立体角足够小，则探测到的光通量可以认为等于qλ, c，而qλ, c满足比尔定律(即式(8)的解)，即
${q_{\lambda ,{\rm{c}}}} = {q_0}{{\rm{e}}^{ - {\beta _\lambda }x}}.$
从而，可据此得出衰减系数表达式[20]
${\beta _\lambda } = - \frac{1}{L}\ln \frac{{{T_{{\rm{n}},\lambda }}}}{{{T_{{\rm{n}},\lambda ,{\rm{ref}}}}}}.$ (10)
根据以上推导过程，虽然对散射相函数没有要求，但是该测量方法忽略了两层玻璃盖板之间的多次反射作用，会引起测量误差.随着光生物反应器内细胞浓度的增加，盖板之间的多次反射作用会发生变化，这会引起测量结果的不确定性.与光谱吸收系数的测量类似，其是否适用于生长期光谱衰减特性的测量需要进行评估.
3 传统测量方法存在的问题及改进方案 3.1 在线测量时传统测量方法存在的问题如上所述，微藻光谱吸收和衰减系数的测量要求满足单散射条件，并且光谱吸收系数的测量还要满足强前向散射条件.在获得光谱吸收和衰减系数测量表达式的过程中忽略了光生物反应器内的多次反射作用, 而微藻在生长的过程中浓度会不断增加，因此不能总是满足单散射条件，并且对光生物反应器内的多次反射作用也会产生影响，如果对生长过程中的微藻进行取样稀释，则会对微藻的生长造成一定的影响.散射相函数因其随生长基本不发生变化，所以测量其稳定期的散射相函数即可.本节定量分析光谱吸收和衰减系数的测量公式应用于光学厚度τ=βL，在不满足单散射条件下产生的误差.引入量纲一参数散射反照率ω=κs/β.定义吸收(衰减)系数的相对误差表达式:
$E = \frac{{\left| {\kappa _{\rm{R}}^{{\rm{exp}}} - \kappa _{\rm{R}}^{{\rm{true}}}} \right|}}{{\kappa _{\rm{R}}^{{\rm{true}}}}} \times 100\% .$
式中:下标R可取a和e，也就是吸收系数和衰减系数.平板式光生物反应器可以看做一个3层介质模型，两侧为玻璃介质中间为微藻混悬液，使用Monte Carlo方法进行模拟计算.计算中两侧玻璃的折射率取ng=1.46，单个玻璃厚度取2 mm.中间微藻混悬液折射率取n=1.34，厚度取10 mm，不对称因子g取0.97.光源为直径4 mm的高斯分布光源.测量衰减系数的探测器直径取4 mm，距离被测样品200 mm.测量吸收系数的探测器直径取10 mm，距离被测样品0 mm.以上参数均是根据实验器材的具体条件参数以及实验对象的光学参数而选取的实际值.
图 5给出了传统测量方法吸收系数和衰减系数相对误差图.从图 5(a)中可以看出，传统测量方法的吸收系数相对误差对光学厚度τ的变化不敏感，但其误差随反照率ω的增加而不断增大.在反照率ω>0.9的情况下，其相对误差>45%.从图 5(b)可以看出，传统测量方法衰减系数相对误差随光学厚度τ和散射反照率ω的增加而增大，但在光学厚度τ < 5的范围内其相对误差 < 10%.
Figure 5
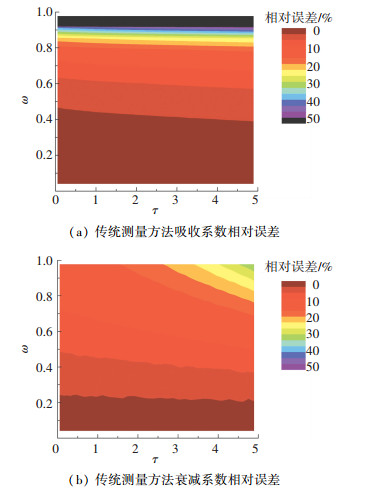图 5 传统测量方法吸收和衰减系数相对误差 Figure 5 The relative error of the traditional absorption and attenuation coefficient measurement method 3.2 改进方案在上述数值模拟中，发现传统测量方法吸收系数的测量误差对光学厚度变化不敏感，主要与反照率相关.当散射反照率＞0.8时，传统测量方法吸收系数的相对误差超过15%.已有的理论及实验研究结果表明，微藻的反照率约为0.9，且具有强前向散射特性，其散射不对称因子约为0.97.由此，本文通过引入修正系数，给出了一种针对传统吸收和衰减系数测量方法的改进方案，改进后的吸收和衰减系数测量公式如下：
${\kappa _{{\rm{a}},\lambda }} = - {f_{{\rm{a}},{\rm{c}}}}\frac{1}{L}\ln \frac{{{T_{{\rm{h}},\lambda }}}}{{{T_{{\rm{h}},\lambda ,{\rm{ref}}}}}},$
${\beta _\lambda } = - {f_{{\rm{e}},{\rm{c}}}}\frac{1}{L}\ln \frac{{{T_{{\rm{n}},\lambda }}}}{{{T_{{\rm{n}},\lambda ,{\rm{ref}}}}}},$
式中fa, c和fe, c分别表示吸收和衰减系数测量方法的修正系数.修正系数是通过大范围的理论计算，对比真实的辐射特性参数(真值)与实验测量值(测量公式(5)、(10)的计算值)之间的差别，由两者的比值获得.下面举例给出了在光学厚度τ=1.0、不对称因子g=0.97以及反照率ω=0.8和0.9的条件下(微藻的反照率一般位于0.7~1.0)的修正系数.在反照率ω=0.8的条件下，传统测量方法吸收和衰减系数的修正系数分别为fa, c=0.870和fe, c=1.025；在反照率ω=0.9的条件下，传统测量方法吸收和衰减系数的修正系数分别为fa, c=0.700和fe, c=1.030，这里给出的修正系数与玻璃的折射率、积分球的开孔尺寸以及探测器的尺寸等因素相关.
图 6给出了改进后的吸收系数测量方法在反照率ω=0.8和0.9情况下的误差图.
Figure 6
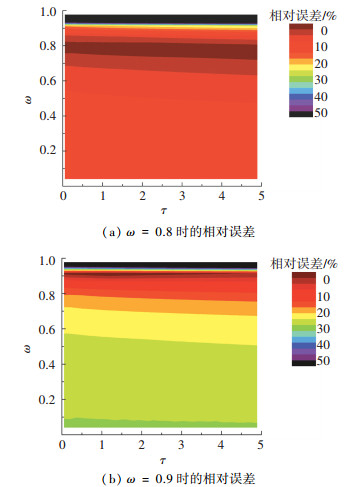图 6 改进方案的吸收系数相对误差 Figure 6 The relative error of the improved absorption coefficient measurement method 从图 6(a)中可以看出，在反照率ω取0.7~0.9时，改进后测量方法的吸收系数相对误差比传统测量方法的有明显减小(在ω=0.8处>15%).从图 6(b)中可以看出，在ω=0.9附近的区间，其相对误差明显减小，相比于传统方法误差降低了45%以上，但ω=0.9时改进的吸收系数测量方法相比于ω=0.8的情况，其误差带变化更剧烈并且较窄.这是由于反照率较大时，吸收系数较小，所以相对误差较大.在反照率ω接近1时，相对误差急剧增大，这是因为此时吸收系数很小(κa ?1)，所以相对误差很大. 图 7给出了在反照率ω=0.8和0.9情况下改进后的测量方法衰减系数的误差图.从图 7中可以看出，改进测量方法的衰减系数在反照率ω取0.5~0.9以及光学厚度τ取(0, 3]时相对误差很小(＜2%)，微藻辐射特性在线测量中，光学厚度τ一般位于0.1~3.0，所以这样的改进方案是具有实际意义的.
Figure 7
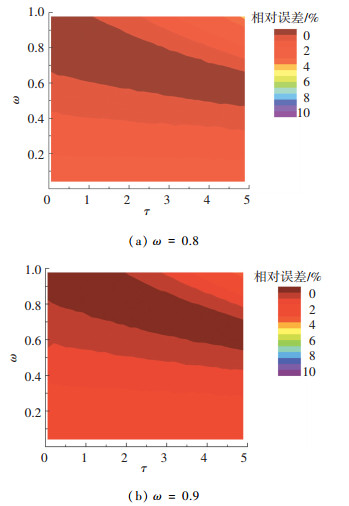图 7 改进方案的衰减系数相对误差 Figure 7 The relative error of the improved extinction coefficient measurement method 图 8给出了以ω=0.8为参考点，传统以及改进方案的吸收和衰减系数在3种典型反照率下的相对误差对比图.从图 8(a)中可以看出，改进测量方法吸收系数相对误差更小(降低了5%以上)，在反照率ω为0.70~0.85时，改进后测量方法吸收系数相对误差在10%以下，而传统方法相对误差＞10%.从图 8(b)中可以看出，在ω=0.8附近，改进测量方法衰减系数相对误差明显减小，在光学厚度τ < 5的范围内，其相对误差 < 2%.改进的衰减系数测量方法明显地降低了误差.
Figure 8
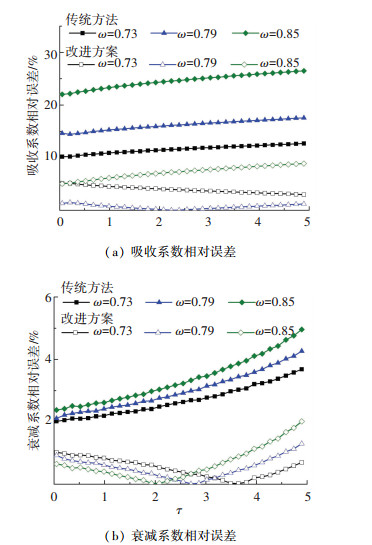图 8 以ω=0.8为参考点，传统与改进方案的吸收和衰减系数的相对误差 Figure 8 The improved proposals based on reference point ω=0.8, the relative error of the absorption and attenuation coefficient measurement method at different albedo 图 9给出了以ω=0.9为参考点，传统以及改进方案的吸收和衰减系数在3种反照率下的相对误差对比图.从图 9(a)中可以看出，改进测量方法的吸收系数在ω=0.9附近大幅度降低了误差(>40%)，从图 9(b)中可以看出，改进测量方法的衰减系数在ω=0.9附近其相对误差明显减小，在光学厚度τ < 3的范围内其相对误差＜2%，明显地降低了测量误差. 图 10给出了修正系数与反照率和光学厚度的变化关系.从图中可以看出，吸收和衰减系数的修正系数对光学厚度的变化不敏感，吸收系数的修正系数随反照率的增加而减小，这是由于反照率较大时，散射相对较强，导致积分球测得的半球透过率偏小，进而获得的吸收系数值偏大.衰减系数的修正系数随反照率的增加呈现线性增大的趋势，但其变化幅度很小，所以可以近似认为衰减系数的修正系数为一个常量(可取反照率ω=0.8、光学厚度τ=1的值).
Figure 9
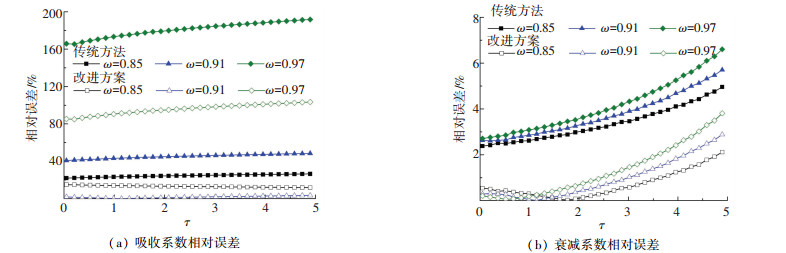图 9 以ω=0.9为参考点, 传统及改进方案的吸收和衰减系数的相对误差 Figure 9 The improved proposals at ω=0.9, the relative error of the absorption and attenuation coefficient measurement method at different albedo Figure 10
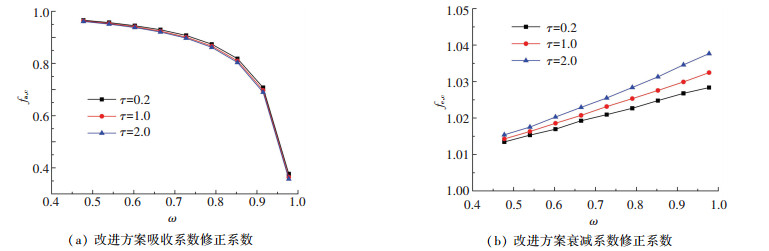图 10 修正系数随反照率和光学厚度的变化 Figure 10 The correction coefficient varying with the scattering albedo and the optical thickness 已有的多种微藻的实验数据[19-20], 其反照率为0.7~1.0，所以本文给出的改进的吸收和衰减系数测量方法对于测量微藻混悬液介质是更有优势的.即改进的吸收和衰减系数测量方法对于测量反照率ω>0.7介质的吸收系数时比传统方法精度更高.综上，微藻的平均反照率大约在0.8~0.9，在微藻辐射特性的在线测量中，平均光学厚度大约在1附近，所以本文给出的改进方案在微藻辐射特性在线测量时，可以大幅度提高微藻光谱吸收和衰减系数的测量精度.
4 微藻细胞生长期辐射特性测量结果图 11给出了实验测量得到的小球藻生长曲线.小球藻的生长可以分为3个阶段：滞后期、指数生长期和稳定期.从图 11中可以看出，前5天为滞后期，其基本特征是生长速率很低，也就是微藻在适应环境; 接着微藻进入指数生长期(5~13)天，这个时期的主要特点是细胞以指数分裂的方式快速增长; 最后微藻进入稳定期，稳定期藻液浓度的波动是由于部分微藻会粘附在反应器内下表面.但这并不影响微藻辐射特性的测量结果，因为在测量透过率和藻液浓度的过程没有计入沉降的细胞，所以实验获得的吸收和散射截面不受藻细胞沉降的影响.
Figure 11
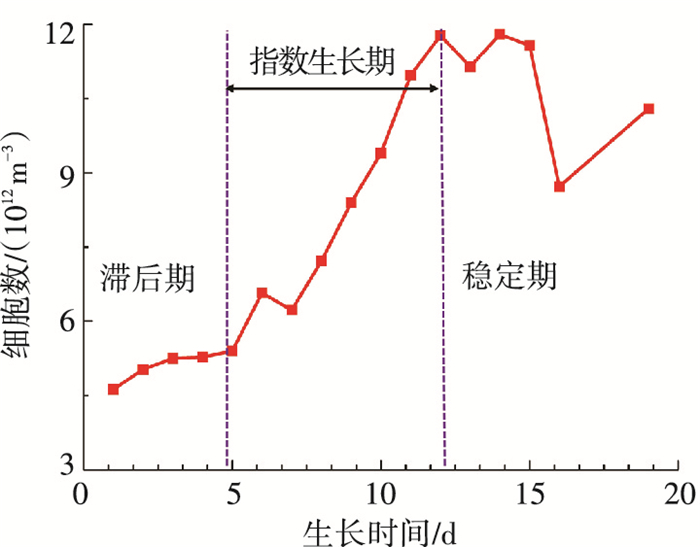图 11 实验测量得到的小球藻细胞生长曲线 Figure 11 The experimental measured cell growth curve of cell density of Chlorella vulgaris 图 12给出了小球藻光谱吸收和衰减截面以及散射反照率随生长时间的变化. 图 12(a)为实验测量的小球藻在380~850 nm光谱范围的不同生长时间的吸收截面变化曲线.图中435 nm和676 nm波长下的吸收峰对应于叶绿素a，485 nm波长下的吸收峰对应于类胡萝卜素[16].
Figure 12
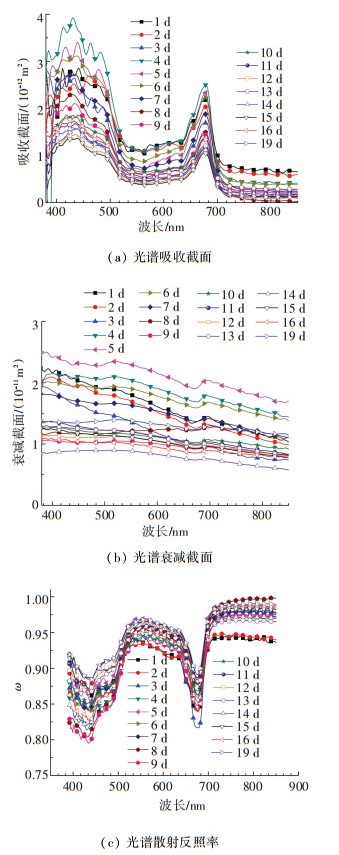图 12 小球藻细胞光谱吸收截面和衰减截面以及散射反照率随生长时间的变化 Figure 12 The spectral absorption cross-sections, attenuation cross-sections and scattering albedo of Chlorella vulgaris varying with the growth times 图 12(b)为实验测量得到的小球藻在380~850 nm光谱范围内的不同生长期衰减截面变化曲线.从图中可以看出，随波长的增加其大致呈减小的趋势.吸收和衰减截面随生长时间变化显著，其相对变化率可分别达167%和178%，所以对微藻生长期的辐射特性研究对于提高光生物反应器中微藻生长率具有重要意义.从图 12(c)中可以看出，小球藻的散射反照率位于0.8到1.0，根据第3节的研究结论可知，使用本文给出的改进的吸收和衰减系数测量方法具有更高的精度.
5 结论微藻细胞生长导致其辐射特性随生长时间发生变化，本文给出了一种可实时在线测量微藻辐射特性的方案.通过分析微藻辐射特性传统测量方法对于生长期辐射特性测量的局限性，并结合微藻细胞辐射特性的特征, 提出了一种改进方法，有效地提高了不同生长阶段及不同浓度下的微藻细胞辐射特性的测量精度.以普通小球藻为例，对其不同生长时间的辐射特性进行了实验研究.得到以下主要结论：
1) 给出了一种可以进行微藻生长期辐射特性的实时在线测量方案，通过定制的平板光生物反应器进行微藻的培养以及微藻光谱衰减系数、光谱吸收系数的测量.所提出的在线测量方案有助于微藻生长相关辐射特性的研究.
2) 提出了微藻辐射特性的改进测量方法，可以对不同光学厚度条件下微藻细胞的光谱衰减系数及光谱吸收系数进行准确测量.对于以ω=0.8为参考点，改进的吸收和衰减系数测量方法在光学厚度小于5(实际测量的微藻混悬液稳定期光学厚度一般小于3)，反照率为0.70~0.85时, 吸收及衰减系数相对误差分别＜10%和2%，而传统测量方法的测量误差则分别＞10%和2%.
3) 普通小球藻的光谱吸收和衰减截面随生长时间变化显著，其相对变化率百分比可分别达到167%和178%.说明对于光生物反应器内光场的准确预测和分析必须使用生长相关的辐射特性，而以往使用稳定生长期辐射特性的测量结果会给光场预测带来较大误差.不同生长期的光谱吸收截面在波长435、676以及485 nm下存在吸收峰，不同生长期的散射反照率＞0.8.
参考文献
[1]CHISTI Y. Biodiesel from microalgae[J].Biotechnology advances, 2007, 25(3): 294-306.DOI: 10.1016/j.biotechadv.2007.02.001
[2]ULLAH K, AHMAD M, SHARMA VK, et al. Assessing the potential of algal biomass opportunities for bioenergy industry: A review[J].Fuel, 2015, 143: 414-423.DOI: 10.1016/j.fuel.2014.10.064
[3]FORJAN E, NAVARRO F, CUARESMA M, et al. Microalgae: Fast-growth sustainable green factories[J].Critical Reviews in Environmental Science and Technology, 2015, 45(16): 1705-1755.DOI: 10.1080/10643389.2014.966426
[4]HALL D O, MARKOV S A, WATANABE Y, et al. The potential applications of cyanobacterial photosynthesis for clean technologies[J].Photosynthesis research, 1995, 46(1/2): 159-167.DOI: 10.1007/bf00020426
[5]SKJ NES K, LINDBLAD P, MULLER J. BioCO2-a multidisciplinary, biological approach using solar energy to capture CO2 while producing H2 and high value products[J].Biomolecular engineering, 2007, 24(4): 405-413.DOI: 10.1016/j.bioeng.2007.06.002
[6]YOON J H, SIM S J, KIM M S, et al. High cell density culture of anabaena variabilis using repeated injections of carbon dioxide for the production of hydrogen[J].International Journal of Hydrogen Energy, 2002, 27(11): 1265-1270.DOI: 10.1016/s0360-3199(02)00109-x
[7]李凤娟, 高大文, 胡晗华. 微藻高CO2耐受机制及其在生物减碳领域的应用[J].哈尔滨工业大学学报, 2015, 47(4): 9-14.
LI Fengjuan, GAO Dawen, HU Hanhua. High-CO2 tolerance mechanisms in microalgae and application to biomitigation[J].Journal of Harbin Institute of Technology, 2015, 47(4): 9-14.DOI: 10.11918/j.issn.0367-6234.2015.04.002
[8]PILON L, BERBEROGLU H, KANDILIAN R. Radiation transfer in photobiological carbon dioxide fixation and fuel production by microalgae[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2011, 112(17): 2639-2660.DOI: 10.1016/j.jqsrt.2011.07.004
[9]CERóN GARCíA M C, SáNCHEZ MIRóN A, FERNáNDEZ SEVILLA J M, et al. Mixotrophic growth of the microalga phaeodactylum tricornutum: Influence of different nitrogen and organic carbon sources on productivity and biomass composition[J].Process Biochemistry, 2005, 40(1): 297-305.DOI: 10.1016/j.procbio.2004.01.016
[10]周集体, 桂冰, 李昂, 等. 气升式光生物反应器中Chlorella sp.优化培养与能量计算[J].哈尔滨工业大学学报, 2015, 47(6): 94-98.
ZHOU Jiti, GUI Bing, LI Ang, et al. Optimization of Chlorella sp. cultivation in airlift photobioreactor and energy calculation[J].Journal of Harbin Institute of Technology, 2015, 47(6): 94-98.DOI: 10.11918/j.issn.0367-6234.2015.06.017
[11]陈智杰, 姜泽毅, 张欣欣, 等. 微藻培养光生物反应器内传递现象的研究进展[J].化工进展, 2012, 31(7): 1407-1413.
CHEN Zhijie, JIANG Zeyi, ZHANG Xinxin, et al. Research progress of transport phenomena within photobioreactor for microalgae culturing[J].Chemical Industry and Engineering Progress, 2012, 31(7): 1407-1413.DOI: 10.16085/j.issn.1000-6613.2012.07.002
[12]CORNET J, DUSSAP C, DUBERTRET G. A structured model for simulation of cultures of the cyanobacterium spirulina platensis in photobioreactors: Ⅰ. coupling between light transfer and growth kinetics[J].Biotechnology and Bioengineering, 1992, 40(7): 817-825.DOI: 10.1002/bit.260400709
[13]CORNET J F, DUSSAP C, GROS J B, et al. A simplified monodimensional approach for modeling coupling between radiant light transfer and growth kinetics in photobioreactors[J].Chemical Engineering Science, 1995, 50(9): 1489-1500.DOI: 10.1016/0009-2509(95)00022-w
[14]MELIS A, NEIDHARDT J, BENEMANN J R. Dunaliella salina (chlorophyta) with small chlorophyll antenna sizes exhibit higher photosynthetic productivities and photon use efficiencies than normally pigmented cells[J].Journal of Applied Phycology, 1998, 10(6): 515-525.DOI: 10.1023/A:1008076231267
[15]HENG R L, PILON L. Time-dependent radiation characteristics of Nannochloropsis oculata during batch culture[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2014, 144: 154-163.DOI: 10.1016/j.jqsrt.2014.04.008
[16]MODEST M F. Radiative heat transfer 2 th ed[M]. New York: Academic press, 2003: 263-286.
[17]BERBEROGLU H, PILON L, MELIS A. Radiation characteristics of Chlamydomonas reinhardtii CC125 and its truncated chlorophyll antenna transformants tla1, tlax and tla1-CW+[J].International Journal of Hydrogen Energy, 2008, 33(22): 6467-6483.DOI: 10.1016/j.ijhydene.2008.07.071
[18]MA C Y, ZHAO J M, LIU L H, et al. GPU-accelerated inverse identification of radiative properties of particle suspensions in liquid by the Monte Carlo method[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2016, 172: 146-159.DOI: 10.1016/j.jqsrt.2015.08.002
[19]BERBEROGLU H, GOMEZ P S, PILON L. Radiation characteristics of Botryococcus braunii, Chlorococcum littorale, and Chlorella sp. Used for CO2 fixation and biofuel production[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2009, 110(17): 1879-1893.DOI: 10.1016/j.jqsrt.2009.04.005
[20]BERBEROGLU H, PILON L. Experimental measurements of the radiation characteristics of Anabaena variabilis ATCC 29413-U and Rhodobacter sphaeroides ATCC 49419[J].International Journal of Hydrogen Energy, 2007, 32(18): 4772-4785.DOI: 10.1016/j.ijhydene.2007.08.018
