陈亮,冯柳,李巧茹
(河北工业大学 土木与交通学院, 天津 300401)
摘要:
为满足客流高峰时段乘客出行舒适度要求，解决公交服务水平低的问题，基于电脑视觉模拟理论，将在车服务水平以立席密度为标准分为4个等级；引入“出行者收入”变量对现有在车感知价值模型进行优化，得到不同服务等级下平均在车感知价值，并考虑乘客感知成本，建立发车间隔计算模型.最后以天津市649路公交数据为例，对模型进行验证，通过MATLAB软件计算出客流高峰时段最优发车间隔.结果表明：高峰客流时段，乘客在车感知成本占总成本的38%~69%，验证了发车间隔计算模型中考虑乘客感知成本的必要性；在保证公交公司基本利益的情况下，最大程度地降低公交出行者的感知成本，充分体现以人为本的服务理念，研究结果可为提高公交系统的吸引力提供理论依据.
关键词: 交通运输系统工程 公共交通 乘客感知价值 发车间隔 在车服务水平
DOI：10.11918/j.issn.0367-6234.201704096
分类号:U491.17
文献标识码:A
基金项目:国家自然科学基金(51678212)
Bus departure interval model considering on-bus perceived value
CHEN Liang,FENG Liu,LI Qiaoru
（School of Civil and transportation, Hebei University of Technology, Tianjin 300401, China）
Abstract:
To satisfy the comfortable demand for passengers during peak period in a low service level, the on-bus service level is divided into four grades with a standard of standing-passenger density based on the theory of computer visual simulation. An improved on-bus perceived value model of different service is proposed with the introduction of passengers' income, and the average of perceived value for different service level under different income of passengers is obtained. Furthermore, the model of departure interval considering passengers' perceived cost is formulated. The model was applied to the 649 bus route in Tianjin City, and the optimal departure time in peak period is derived based on MATLAB. Results show that it is necessary to consider passenger's perceived cost when the on-bus perceived value is 38%-69% in total during peak period. Passenger's perceived cost is cut down sharply while bus company basic interests be guaranteed. It reflects people-based service concept and may provide important scientific support with promoting the attraction of bus systems.
Key words: engineering of communications and transportation system public transportation passenger perceived value departing interval on-bus service level
陈亮, 冯柳, 李巧茹. 考虑在车感知价值的公交发车间隔计算模型[J]. 哈尔滨工业大学学报, 2018, 50(3): 150-155. DOI: 10.11918/j.issn.0367-6234.201704096.
CHEN Liang, FENG Liu, LI Qiaoru. Bus departure interval model considering on-bus perceived value[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 150-155. DOI: 10.11918/j.issn.0367-6234.201704096.
基金项目 国家自然科学基金(51678212) 作者简介 陈亮(1978—)，男，副教授 通信作者 李巧茹，qiaoruli129@126.com 文章历史 收稿日期: 2017-04-19
Contents -->Abstract Full text Figures/Tables PDF
考虑在车感知价值的公交发车间隔计算模型
陈亮, 冯柳, 李巧茹
河北工业大学 土木与交通学院，天津 300401
收稿日期: 2017-04-19
基金项目: 国家自然科学基金(51678212)
作者简介: 陈亮(1978—)，男，副教授
通信作者: 李巧茹，qiaoruli129@126.com
摘要: 为满足客流高峰时段乘客出行舒适度要求，解决公交服务水平低的问题，基于电脑视觉模拟理论，将在车服务水平以立席密度为标准分为4个等级；引入“出行者收入”变量对现有在车感知价值模型进行优化，得到不同服务等级下平均在车感知价值，并考虑乘客感知成本，建立发车间隔计算模型.最后以天津市649路公交数据为例，对模型进行验证，通过MATLAB软件计算出客流高峰时段最优发车间隔.结果表明：高峰客流时段，乘客在车感知成本占总成本的38%~69%，验证了发车间隔计算模型中考虑乘客感知成本的必要性；在保证公交公司基本利益的情况下，最大程度地降低公交出行者的感知成本，充分体现以人为本的服务理念，研究结果可为提高公交系统的吸引力提供理论依据.
关键词: 交通运输系统工程 公共交通 乘客感知价值 发车间隔 在车服务水平
Bus departure interval model considering on-bus perceived value
CHEN Liang, FENG Liu, LI Qiaoru
School of Civil and transportation, Hebei University of Technology, Tianjin 300401, China
Abstract: To satisfy the comfortable demand for passengers during peak period in a low service level, the on-bus service level is divided into four grades with a standard of standing-passenger density based on the theory of computer visual simulation. An improved on-bus perceived value model of different service is proposed with the introduction of passengers' income, and the average of perceived value for different service level under different income of passengers is obtained. Furthermore, the model of departure interval considering passengers' perceived cost is formulated. The model was applied to the 649 bus route in Tianjin City, and the optimal departure time in peak period is derived based on MATLAB. Results show that it is necessary to consider passenger's perceived cost when the on-bus perceived value is 38%-69% in total during peak period. Passenger's perceived cost is cut down sharply while bus company basic interests be guaranteed. It reflects people-based service concept and may provide important scientific support with promoting the attraction of bus systems.
Key words: engineering of communications and transportation system public transportation passenger perceived value departing interval on-bus service level
近年来，公交客流高峰时段满载率高导致的乘客满意度差已成为公交调度中不可忽视的问题.在公交出行过程中，车内立席密度增大或车外候车时间增加，都会使乘客产生焦急情绪，导致效用损失，进而影响乘客对出行方式的选择.因此，将量化的乘客主观感知，包括在车感知和候车感知，考虑到公交调度中，是改善公共交通服务质量的重要措施.
国内外学者对于公交发车间隔的研究较多，直到近年来，研究的热点逐渐由公交服务主体导向转变为客体导向，模型中更着重考虑乘客成本，注重乘客满意度，即本文讨论的乘客感知.当前考虑乘客感知的发车间隔研究主要采用满意隶属度[1]、损失成本[2]、满意乘客数占总人数比例[3]等表示乘客在车满意度，或者集中倾向于沿用传统方法，引入固定转换系数将在车感知价值损失转化为出行成本[4]，虽然考虑了乘客满意度对发车间隔的影响，但未将乘客在车感知进行具体量化；文献[5]将损失风险及期望效用理论与乘客等待公交时的心理变化相结合，反应不同等待时间对乘客情绪的影响，得到基于乘客候车满意度的最优发车间隔；文献[6]将公交线路划分成3种不同模式，并应用线路OD点计算出不同模式下的优化指标，结果表明对乘客出行成本考虑越全面，对发车频率要求越高；文献[7]通过建立回归模型并进行检验，考察影响乘客候车心理因素，得出提供实时时间信息比增加车次让乘客感觉等待时间更短，以上文献侧重候车感知的影响因素分析及研究.文献[8]考虑车内感知，建立了基于最大感知和平均感知的公交调度优化模型，但没有将候车感知与在车感知相结合.
综上所述，大部分学者在研究发车间隔时将重点放在候车满意度(即候车感知)上，对乘客由于拥挤产生的在车感知价值损失研究较少，而目前国内公交车拥挤现象频繁，导致乘客在车感知在出行过程中的作用不容忽视；虽然有部分文献将乘客感知考虑到发车间隔计算模型中，但没有将模型中涉及的乘客感知进行具体量化，也未明确指出其与发车间隔的关系.基于此，本文从乘客感知出发，引入收入变量，建立不同服务等级下不同收入水平乘客在车感知价值模型；并结合候车感知成本，建立发车间隔计算模型，以期满足高峰时段乘客出行需求，增加公共交通吸引力.
1 公交在车服务等级划分国外将公交服务水平按承载率LF分级[9]，以LF>1.5作为在车拥挤标准；中国客车装载质量计算方法[10]规定城市公共汽车允许站立面积为0.125 m2/人，由此核算LF=2.1记为超载(按国内一般座位数为36，站立面积为5 m2的公交车型来计算)，显然，考虑国内外乘客行为与公交车车型等因素差异，国内公交车经常出现乘客大面积站立情况，尤其客流高峰期频繁出现车满为患的现象，因此，不能照搬国外公交服务质量分级.针对国内公交车客流高峰期运营现状，以车内站立乘客为研究对象，选择不同立席密度下乘客感知作为在车服务等级的划分依据.
立席密度即站立乘客与可站立面积比值，与承载率之间关系为
${L_F} = \left( {A \times d + s} \right)/s.$ (1)
式中：A为公交车内可站立面积，m2；d为立席密度，人/m2；s为公交车座位数.
为了解出行过程中在车感知对乘客的影响，2017年4月7日—10日分别选取工作日和非工作日高峰时段，在天津市开展不同立席密度下公交出行跟车调查和在车服务水平分级问卷调查.总结讨论跟车访谈过程中随立席密度增加乘客心理感知的变化过程，将在车服务水平划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ4个等级，对应的拥挤特征为：当只有少数人站立时，每位乘客都有充足的站立空间；随着立席密度增加，乘客开始感觉拥挤；当立席密度接近国家规定值d=8时，人与人之间已不足陌生人的安全距离，拥挤感开始强烈；当立席密度超过额定值时，乘客对拥挤的感知非常强烈，甚至会出现“单脚站立”的现象.
在问卷调查过程中，鉴于在实际运营公交车中寻找不同立席密度状态存在一定困难，数字和语言描述又很难让受访者形象直观地了解车内状况，因此本文采用电脑视觉模拟方法，对不同立席密度下公交出行情境进行模拟，部分模拟情景如图 1所示.该方法出现在文献[11]中，用于游憩区乘客感知拥挤调查，之后被普遍应用在旅游管理等相关领域.以图片呈现方式供受访者进行视觉评价，更具直观性，符合本文调查需求和特点.
Figure 1
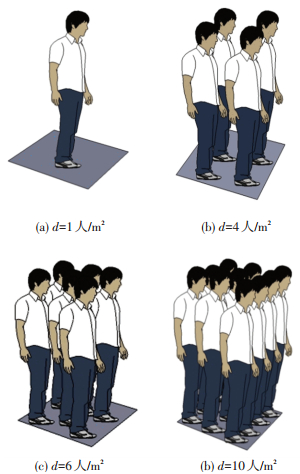图 1 不同立席密度模拟效果图 Figure 1 Simulation results under different standing-passenger density 受访者考虑出行感知，包括拥挤产生的疲劳、烦躁等无形损失，对出行选择及服务水平进行判断.对回收的495份有效问卷进行筛选和有效性处理，最终得到463份有效样本，通过对不同立席密度下乘客出行选择进行分析，得到立席密度分别为0，1，2，3，4，5，6，7，8，9，10，11时对应的公交出行选择率分别为100%，99.3%，94.5%，91.3%，84.3%，73.1%，50.64%，30.12%，10.6%，5.6%，3.2%，1.3%.
用k表示在车服务等级，设k∈{Ⅰ, Ⅱ, Ⅲ, Ⅳ}，Bk(d)表示立席密度d属于某一在车服务等级k的程度，在客流高峰期，公交车内每平方米站立人数可达11人之多[12]，因此将隶属度函数中立席密度的取值范围确定为[0, 11].车内乘客根据自身拥挤感知判断当前状态所属服务等级，将模糊概念明确化，若运营车辆处于d=3状态，16.4%的乘客认为属于Ⅰ服务等级，有充足的站立空间；83.1%的乘客认为属于Ⅱ服务等级，开始感觉拥挤；0.5%的乘客认为属于Ⅲ服务等级，拥挤感开始强烈，则将d=3对Ⅰ、Ⅱ、Ⅲ等级的隶属频率分别记为16.4%、83.1%、0.5%，综合不同拥挤程度下的跟车调查结果和乘客对不同立席密度所属服务等级的认知，统计得到各服务等级立席密度隶属频率见表 1.
表 1
表 1 各服务等级立席密度隶属频率 Table 1 Membership frequency of passenger-standing density for each service level 立席密度/(人/m2)隶属频率/%
Ⅰ等级 Ⅱ等级 Ⅲ等级 Ⅳ等级
0 100 — — —
1 99.1 0.9 — —
2 96.3 3.7 — —
3 16.4 83.1 0.5 —
4 0.4 81.4 18.2 —
5 — 69.3 30.7 —
6 — 0.6 97.2 2.2
7 — — 90.1 9.9
8 — — 26.7 73.3
9 — — — 100
10 — — — 100
11 — — — 100
表 1 各服务等级立席密度隶属频率 Table 1 Membership frequency of passenger-standing density for each service level
结合表 1的实验调查结果，得到隶属度函数，见式(2)~(5)，函数如图 2所示.
Figure 2
图 2 在车服务等级隶属度函数图 Figure 2 Membership grade function for service level in bus ${B_1}\left( d \right) = \left\{ \begin{array}{l}1,0 \le d < 2;\\3 - d,2 \le d < 3;\\0,3 \le d \le 11.\end{array} \right.$ (2)
${B_2}\left( d \right) = \left\{ \begin{array}{l}0,0 \le d < 2;\\d - 2,2 \le d < 3;\\1,3 \le d < 4;\\6 - d/2,4 \le d < 6;\\0,6 \le d < 11.\end{array} \right.$ (3)
${B_3}\left( d \right) = \left\{ \begin{array}{l}0,0 \le d < 5;\\d - 5,5 \le d < 6;\\1,6 \le d < 7;\\8 - d,7 \le d < 8;\\0,8 \le d < 11.\end{array} \right.$ (4)
${B_4}\left( d \right) = \left\{ \begin{array}{l}0,0 \le d < 7;\\d - 7,7 \le d < 8;\\1,8 \le d \le 11.\end{array} \right.$ (5)
结合图 2，根据最大隶属度原则，取相邻两个服务等级隶属度函数的相交点作为相邻服务等级立席密度的分界点，从而确定Ⅰ、Ⅱ、Ⅲ、Ⅳ在车服务等级对应的立席密度区间分别为[0, 2.5]、(2.5, 5.34]、(5.34, 7.5]、(7.5, 11].
2 不同服务等级下在车感知价值将在车服务等级以立席密度为标准分为Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个等级，分别表征车内不同拥挤程度.采用标准binary logistic模型作为个体出行选择模型形式[13]，依据出行过程中服务等级选择与出行方式选择的相似性，建立不同拥挤程度下个体出行选择行为效用函数及在车感知价值计算模型[14]分别为
${Y_k} = {\alpha _k}c + {\beta _k}t + {A_J},$ (6)
${f_k}\left( t \right) = {\beta _k}/{\alpha _k}.$ (7)
式中：Yk为k级服务等级下乘客选择公交的出行效用；αk, βk分别为乘车费用、乘车时间系数；c为乘车费用，元；t为乘车时间，min；AJ为常数项；fk(t)为k级服务等级下个体乘客的在车感知价值.
该模型在建立不同拥挤程度下的出行效用函数时，主要考虑了出行费用和时间的影响.而不同收入出行者的消费观念和习惯不同，对在车拥挤程度的敏感性也有所不同，出行者收入会影响函数中出行费用c对效用Yk的贡献率，即αk，已有研究针对乘车费用系数αk与收入变量I的关系, 提出了αk=μk+δk/I、αk=μk+δk/LnI和αk=μk+δk/Iθ3种关系，并通过回归分析确定了收入变量为对数形式时的模型为最优[15]，在此基础上，选取两者关系式为
${\alpha _k} = {\mu _k} + \frac{{{\delta _k}}}{{{L_n}I}}.$ (8)
式中μk、δk为待标定参数；I为乘客收入，元/月.
基于以上研究，本文引入出行者收入变量对原有模型进行优化，构造不同服务等级下乘客选择公交出行的效用函数为
${Y_k} = \left( {{\mu _k} + \frac{{{\delta _k}}}{{{L_n}I}}} \right)c + {\beta _k}t + {A_J}.$ (9)
其中μk、δk、βk、AJ通过SPSS软件的回归分析拟合结果进行标定，k级在车服务等级下，不同收入水平乘客的感知价值计算模型为
$F\left( {{d_k}} \right) = \frac{{{\beta _k}}}{{{\mu _k} + {\delta _k}{{\left( {{L_n}I} \right)}^{ - 1}}}}.$ (10)
根据研究地区公交出行乘客实际经济收入状况，将收入水平分为N个区间，计算相应乘客比例，建立平均在车感知价值计算模型为
$\begin{array}{*{20}{c}}{\bar F\left( {{d_k}} \right) = F\left( {{d_{k1}}} \right){\gamma _1} + F\left( {{d_{k2}}} \right){\gamma _2} + }\\{ \cdots + F\left( {{d_{kN}}} \right){\gamma _N}.}\end{array}$ (11)
式中：F(dk1)，F(dk2)，…，F(dkN)为k级服务等级下不同收入乘客在车感知价值；γ1，γ2，…，γN分别为不同收入区间乘客所占比例，可通过实地调查得到；F(dk)为k级服务等级下乘客平均在车感知价值.
3 发车间隔计算模型 3.1 模型准备由于公交系统的庞大与复杂，行驶过程中受外界因素影响较大，因此对公交车辆调度过程作如下假设：1)车辆运行速度保持不变，即路段运行时间仅与路段长度有关；2)不存在车辆越站和超车的现象；3)在研究时间段内，车辆发车间隔固定；4)同一线路上所有公交车为同一型号，且都为前门上车、后门下车；5)固定需求下的乘客出行OD矩阵是确定的，不考虑公交线网中其他班次公交的影响.
符号及变量说明如下：F(t)为平均候车感知价值，元/(人·h)；Qij为第i站等候第j辆车乘客数；tij－1为第j－1辆车到达第i站的时间；tij为第j辆车到达第i站的时间；λi(t)为第i站乘客平均到达率，人/min；Tij为第j辆车在第i站的停靠时间，min；a、b分别为乘客平均上、下车时间，min/人；Qi－1, ij为第j辆车在i－1至i站的断面载客量，人；qij为第j辆车在i站的下车比例，下车人数占车上总人数比例；H为建立发车间隔模型时基于的时间长度，min；h为发车间隔，min；hmax、hmin为H时间段内的最大、最小发车间隔，min；m为H时间段内发车数量；n为线路站点个数；di－1, ij为第j辆车在i－1至i站断面立席密度，人/m2；dij为第j辆车在i站节点处立席密度，人/m2；F(di－1, ij)为第j辆车在i－1至i站个体乘客平均在车感知价值，元/(人·h)；F(di－1, ij)为第j辆车在i－1至i站的在车感知总成本，元；v为车辆平均行驶速度，km/h；li－1, i为i－1至i站点之间线路距离，km；L为线路总长度，km；C为公交车单位变动运营成本，元/(辆·km).
3.2 模型建立个体乘客在出行过程中，会产生感知价值，而在建立发车间隔计算模型的过程中，感知价值的损失被视为感知成本处理，则研究时间段内乘客出行感知总成本如下.
1) 乘客候车感知总成本.通过对候车感知时间价值进行研究[16]，得到不同候车时间区间对应的乘客平均感知候车时间价值为
$\bar F\left( t \right) = \left\{ \begin{array}{l}{\eta _1}{\gamma _1} + {\eta _2}{\gamma _2} + \cdots {\eta _N}{\gamma _N},0 \le t \le 6;\\{\tau _1}{\gamma _1} + {\tau _2}{\gamma _2} + \cdots {\tau _N}{\gamma _N},6 < t \le 14.\end{array} \right.$ (12)
式中：η1，η2…ηN，τ1, τ2，…，τN分别为不同候车时间对应的乘客候车感知价值，进而得到乘客候车感知总成本为
$\begin{array}{l}{W_{\rm{D}}} = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {Q_i^j\left( {t_i^j - t_i^{j - 1}} \right)} } \times \bar F\left( t \right)/60 = \\\;\;\;\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{\lambda _i}\left( t \right){{\left( {t_i^j - t_i^{j - 1}} \right)}^2}} } \times \bar F\left( t \right)/60.\end{array}$ (13)
2) 站立乘客在车感知总成本.在研究时间段内，将乘客出行过程中所有站点间的在车感知成本进行累计，得到站立乘客在车感知总成本WZ.计算各站点之间的立席密度为
$\begin{array}{l}d_{i - 1,i}^j = h\left[ {{\lambda _1}\left( t \right)\prod\limits_{k = 2}^{i - 1} {\left( {1 - {q_k}} \right)} + {\lambda _2}\left( t \right)\prod\limits_{k = 3}^{i - 1} {\left( {1 - {q_k}} \right)} + } \right.\\\;\;\left. { \cdots + {\lambda _{i - 2}}\left( t \right)\left( {1 - {q_{i - 1}}} \right) + {\lambda _{i - 1}}\left( t \right)} \right] - s/A.\end{array}$ (14)
在计算相邻站点间在车感知成本时，对公交站点节点处感知成本的处理如图 3所示.
Figure 3
图 3 站点示意图 Figure 3 Example of bus stations 对第i站停靠时间内的立席密度作近似处理，即dij=di－1, ij，并归到i－1至i站断面计算；车辆在第i站的停靠时间Tij取乘客上、下车总时间的最大值为
$T_i^j = \max \left\{ {\bar a{\lambda _i}\left( t \right)h,\bar bQ_{i - 1,i}^j{q_i}} \right\}.$ (15)
则相邻站点之间的在车感知成本、站立乘客在车感知总成本分别为
$\begin{array}{*{20}{c}}{F\left( {d_{i - 1,i}^j} \right) = \left( {Q_{i - 1,i}^j - s} \right)\left( {{l_{i - 1,i}}/v + } \right.}\\{\left. {\max \left\{ {\bar a\lambda _{i - 1}^j\left( t \right)h,\bar bQ_{i - 2,i - 1}^jq_{i - 1}^j} \right\}} \right)\bar F\left( {d_{i - 1,i}^j} \right)/60,}\end{array}$ (16)
${W_Z} = \sum\limits_{i = 2}^n {\sum\limits_{j = 1}^m {F\left( {d_{i - 1,i}^j} \right)} } ,$ (17)
3) 公交公司成本为
${W_G} = C\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^m {\left( {t_i^j - t_{i - 1}^j} \right)} } .$ (18)
4) 总成本W计算过程.简化tij－tij－1=h，得到最小化乘客感知成本和公交公司变动运营成本之和的发车间隔计算模型，目标函数为
$\begin{array}{l}\min \left\{ {\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^m {\left[ {\left( {Q_{i - 1,i}^j - s} \right)\left( {{l_{i - 1,i}}/v + } \right.} \right.} } } \right.\\\;\;\;\left. {\left. {\max \left\{ {\bar a\lambda _{i - 1}^j\left( t \right)h,\bar bQ_{i - 2,i - 1}^jq_{i - 1}^j} \right\}} \right)\bar F\left( {d_{i - 1,i}^j} \right)/60} \right] + \\\;\;\;\left. {\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{\lambda _i}\left( t \right){h^2}\bar F\left( t \right)/60} } + 60CHL/h} \right\}.\end{array}$ (19)
目标函数约束条件为
$\left\{ \begin{array}{l}{h_{\min }} \le h \le {h_{\max }},\\d_{i - 1,i}^j > 0,\forall i,j.\end{array} \right.$ (20)
4 实证分析以天津市649线路为研究对象，全程21个站点共15.12 km，平均行驶速度为18 km/h，选取高峰客流时段H=2 h，发车间隔为10~15 min，即hmin=10 min，hmax=15 min. 649为31座车型(包括一个驾驶员座位)可站立面积为6 m2，前门上车，后门下车，单位变动运营成本C=1.54元. 649公交线路的部分站点是轨道交通覆盖不到的城区边缘，公交客流具有高峰时段流量大，乘客收入差异较大等特点.拟合不同在车服务等级下乘客出行效用函数分别为
${Y_{\rm{I}}} = \left( {1.854 - \frac{{24.71}}{{{L_n}I}}} \right)c - 3.08t - 0.146,$
${Y_{{\rm{II}}}} = \left( {3.152 - \frac{{35.48}}{{{L_n}I}}} \right)c - 3.64t - 0.265,$
${Y_{{\rm{III}}}} = \left( {1.02 - \frac{{13.89}}{{{L_n}I}}} \right)c - 5.56t - 0.102,$
${Y_{{\rm{IV}}}} = \left( {0.186 - \frac{{10.325}}{{{L_n}I}}} \right)c - 12.73t - 0.639.$
由于天津实行小汽车限行政策，存在部分月薪过万人群一周会有一天选择“轨道交通”或者“轨道交通+公交”的出行模式，因此根据实际公交出行情况，将乘客收入水平划分为6个区间，计算得到不同在车服务等级下不同收入水平乘客的在车感知价值见表 2，其变化规律如图 4所示.
表 2
表 2 不同服务等级下不同收入水平乘客在车感知价值 Table 2 Perceived value in bus of various income passengers under differential service levels 收入(千元/月) 感知价值/(元/(人·h)) Ⅰ等级 Ⅱ等级 Ⅲ等级 Ⅳ等级
0~3 2.02 2.14 6.32 10.38
3~5 2.74 3.23 8.49 12.02
5~8 3.21 4.09 9.89 12.86
8~12 3.72 5.2 11.39 13.61
12~20 4.41 7.09 13.4 14.46
≥20 4.80 8.45 14.53 14.86
表 2 不同服务等级下不同收入水平乘客在车感知价值 Table 2 Perceived value in bus of various income passengers under differential service levels
Figure 4
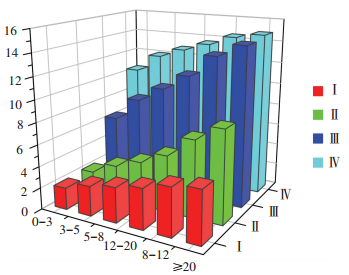图 4 不同在车服务等级下不同收入水平乘客在车感知价值 Figure 4 Perceived value in bus of various income passengers under differential service levels 由图 4可知，随着在车服务水平下降，在车感知价值增大，表明车内立席密度越大，乘客为摆脱这种环境的意愿越强烈，愿意支付费用越多.当在车服务等级为Ⅰ、Ⅱ时，不同收入水平乘客的支付意愿明显不同，随收入增加，在车感知价值不断增大，平均增长率达到32%.说明拥挤程度在可接受范围内时，收入水平对在车感知价值影响较大，收入越高的人群愿意支付越多；而当车上立席密度达到一定程度属于Ⅳ级时，虽然感知价值明显增大，但平均增长率只有7%.说明车上非常拥挤时，收入水平对在车感知价值影响较小，乘客都愿意为改变特别拥挤的状态而支付一定费用.
本文建立模型的目标函数为单一变量的非线性规划函数，因此采用一维搜索方法求解.结合调查数据，按不同候车区间在MATLAB软件中分段编写总成本最小的目标函数文件，发车间隔h为目标函数中的独立变量，总费用为返回值，确定使目标函数最小的整数发车间隔h.通过计算，得到该时段内的最优发车间隔为12 min，计算具体结果见表 3.
表 3
表 3 成本计算结果汇总表 Table 3 Summary of cost calculation results 发车间隔/min WZ/元) WD/元) WG/元 W/元 10 278.36 168.13 279.42 725.92
11 282.14 184.95 254.02 721.1
12 284.79 201.76 232.85 719.4
13 810.83 265.65 214.94 1 291.42
14 870.69 286.09 199.58 1 356.36
15 1086.82 306.52 186.28 1 579.62
表 3 成本计算结果汇总表 Table 3 Summary of cost calculation results
由表 3可知，当发车间隔由10 min提高为12 min时，总成本降低0.9%，虽然乘客在车感知成本提高了2.31%，但是公交公司成本降低16.67%.当发车间隔由15 min降低为12 min时，在公交公司成本仅提高25%的情况下，总成本却大幅度降低，达到54.46%，原因是乘客在车感知成本降低了73.8%.在高峰客流时段，乘客的在车感知成本达到总成本的38%~69%，说明在车感知成本的重要性.显然，随着发车间隔增大，在车感知成本快速增加，而公交企业成本增加速率较小.因此，从长远角度考虑，公交公司可以在客流高峰时段适当减小发车间隔来提升服务水平，以增强客流吸引力，在保证自身成本变动不大的基础上实现社会总效益最大化.
5 结论1) 基于电脑视觉模拟理论，开展乘客感知与公交在车服务水平关系的调查研究，提出了一套服务等级划分和度量的方法，并将在车服务等级划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个等级，依据最大隶属度原则，得到对应立席密度区间分别为[0, 2.5]、(2.5, 5.34]、(5.34, 7.5]、(7.5, 11].
2) 将出行者收入引入出行效用函数，得到改进的在车感知价值计算模型；优化后模型能反映不同收入水平对感知价值的影响及其变化规律.
3) 综合考虑在车和候车感知成本，度量乘客出行满意度，建立面向乘客的发车间隔计算模型，以天津市649公交线路为例，对模型进行了分析求解.结果表明，乘客在车感知成本是公交出行成本中不可忽视的重要组成部分，求解得到的最优发车间隔实现了总成本最小化的目标.
4) 针对固定需求下单线路公交建立了考虑乘客感知的发车间隔计算模型，进一步的研究将考虑具有竞争性的多条公交线路，考虑弹性需求客流特点，分别从社会效益最优和乘客出行均衡的角度完善和改进模型.
参考文献
[1] 牛学勤, 陈茜, 王炜. 城市公交线路调度发车频率优化模型[J]. 交通运输工程学报, 2003, 3(4): 68-72.
NIU Xueqin, CHEN qian, WANG wei. Optimal model of urban bus frequency determination[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4): 68-72. DOI:10.3321/j.issn:1671-1637.2003.04.016
[2] 姚俊, 吕智林, 叶嫣. 基于满意度的公交车调度模型研究[J]. 交通信息与安全, 2009, 27(4): 67-69.
YAO Jun, LV Zhilin, YE Yan. Model for bus dispatching based on satisfaction[J]. Journal of Transport Information and Safety, 2009, 27(4): 67-69. DOI:10.3963/j.ISSN1674-4861.2009.04.016
[3] 曹亦文, 巨永锋, 陈锋. 城市公交车发车频率优化模型[J]. 安徽大学学报(自然科学版), 2007, 31(2): 29-32.
CAO Yiwen, JU Yongfeng, CHEN feng. Optimal model of urban bus frequency[J]. Journal of Anhui University (Natural Sciences), 2007, 31(2): 29-32. DOI:10.3969/j.issn.1000-2162.2007.02.008
[4] 姚宝珍, 杨成永, 沈飞, 等. 基于综合集成赋权法的公交发车频率优化模型[J]. 交通运输系统工程与信息, 2011, 11(2): 124-129.
YAO Baozhen, YANG Chengyong, SHEN Fei, et al. Bus frequency optimization model based on using synthetic evaluation[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(2): 124-129. DOI:10.3969/j.issn.1009-6744.2011.02.019
[5] 贾彦鹤. 考虑乘客满意度的公交发车间隔优化[D]. 成都: 西南交通大学, 2013.
JIA Yanhe. Optimal bus schedule based on passenger satisfaction[D]. Chengdu: School of Economics and Management, Southwest Jiaotong University, 2013.
[6] LEIVA C, MUNOZ J C, GIESEN R, et al. Design of limited-stop services for an urban bus corridor with capacity constraints[J]. Transportation Research Part B: Methodological, 2010, 44(10): 1186-1201. DOI:10.1016/j.trb.2010.01.003
[7] WATKINS K E, FERRIS B, BORNING A, et al. Where is my bus? impact of mobile real-time information on the perceived and actual wait time of transit riders[J]. Transportation Research Part A Policy & Practice, 2011, 45(8): 839-848.
[8] 杨熙宇, 暨育雄, 张红军. 基于感知的公交调度发车频率和车型优化模型[J]. 同济大学学报(自然科学版), 2015, 43(11): 1684-1688.
YANG Xiyu, JI Yuxiong, ZHANG Hongjun. Bus service frequency and bus size optimization model considering passengers'perception[J]. Journal of Tongji University (Natural Science), 2015, 43(11): 1684-1688. DOI:10.11908/j.issn.0253-374x.2015.11.011
[9] KFH Group. Transit capacity and quality of service manual[M]. 3th ed. Washington DC: TRB, 2013.
[10] 客车装载质量计算方法: GB/T 12428—2005. [S]北京: 中国标准出版社, 2005.
[11] MANNING R E. Social carrying capacity of natural areas: theory and application in the U.S. National Parks[J]. Natural Areas Journal, 1996, 16(2): 118-127.
[12] 张君丽. 公共汽车内部空间及设施的研究[D]. 武汉: 湖北工业大学, 2007.
ZHANG Junli. Bus inside space and the facilities research[D]. Wuhan: Hubei University of Technology, 2007.
[13] 王殿海, 叶盈, 朱文韬, 等. 基于条件价值法的公交车内拥挤成本测算模型[J]. 吉林大学学报(工学版), 2014, 46(1): 57-62.
WANG Dianhai, YE Ying, ZHU Wentao, et al. Estimation of crowding costs in bus based on contingent valuation method[J]. Journal of Jilin University (Eng and Technol Ed), 2014, 46(1): 57-62. DOI:10.13229/j.cnki.jdxbgxb201601009
[14] 邵敏华, 李田野, 孙立军. 常规公交乘客对车内拥挤感知阻抗调查与建模[J]. 同济大学学报(自然科学版), 2012, 40(7): 1031-1034.
SHAO Minhua, LI Tianye, SUN Lijun. Survey method and model of passengers' cost perception of crowding level in bus[J]. Journal of Tongji University (Natural Science), 2012, 40(7): 1031-1034. DOI:10.3969/j.issn.0253-374x.2012.07.012
[15] 陈旭梅, 刘巧仙, 杜光. 基于SP调查的城市公共交通出行时间价值估计[J]. 交通运输系统工程与信息, 2011, 11(4): 77-84.
CHEN Xumei, LIU Qiaoxian, DU Guang. Estimation of travel time values for urban public transport passengers based on SP survey[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4): 77-84. DOI:10.3969/j.issn.1009-6744.2011.04.012
[16] 吕慎, 陶流洋, 莫一魁. 通勤出行公交候车时间的服务等级划分和度量[J]. 交通运输系统工程与信息, 2015, 15(3): 190-195, 221.
LV Shen, TAO Liuyang, MO Yikui. Level of service classification and quantification for bus waiting time on commuting trip[J]. Journal of Transportation Systems Engineering and Information, 2015, 15(3): 190-195, 221. DOI:10.3969/j.issn.1009-6744.2015.03.030
