秦胜伍,马中骏,陈骏骏,吕江峰,陈剑平,曹荣国
(吉林大学 建设工程学院,长春 130026)
摘要:
为综合分析参数具有多种不确定性的楔体的稳定性，提出一种基于Fisher最优分割法和盲数理论的楔体稳定性概率分析方法，该方法通过构造基于Fisher最优分割法的楔体稳定性盲数评价模型，综合考虑楔体参数的多种不确定性，确定楔体稳定性概率分布.文章构建了单滑面与双滑面的不确定性楔体稳定性盲数评价模型，将该模型应用于经典的双滑面楔体稳定性分析之中，并与传统的均值安全系数、数值模拟、蒙特卡洛抽样(MCS)方法的结果进行对比，结果表明：均值安全系数法和swedge数值分析只能给出一个固定的安全系数，准确度较低，不能考虑楔体的失稳概率，基于Fisher最优分割法和盲数理论的楔体稳定性分析方法安全系数累计频率与公认比较准确的蒙特卡洛抽样方法几乎重合，并且更加的高效简便，验证了该方法的可靠性与有效性.最后，将该方法应用于兴城某楔体的稳定性评价，为楔体的防治提供数据支撑.
关键词: 楔体 不确定性 Fisher最优分割 盲数理论 概率分析 蒙特卡洛模拟
DOI：10.11918/j.issn.0367-6234.201705028
分类号:TU457
文献标识码:A
基金项目:国家自然科学基金青年基金(41202197)； 国家自然科学基金重点项目(41330636)
Probability analysis method and application of wedge stability
QIN Shengwu,MA Zhongjun,CHEN Junjun,Lü Jiangfeng,CHEN Jianping,CAO Rongguo
(College of Construction Engineering, Jilin University, Changchun 130026, China)
Abstract:
To comprehensively analyze the wedge stability whose parameters have various uncertainties, a method was proposed to analyze the stability of wedge probability based on blind data theory and Fisher optimal segmentation method. A blind data evaluation model of wedge stability considering a variety of wedge parameter uncertainties was created to determine the wedge stability. The evaluation model of the blind number of the stability of the wedge was given, and the model was applied to the classical double-wedge stabilization, in which the result was compared with that from the traditional mean safety coefficient, numerical simulation, and Monte Carlo sampling (MCS). The compared results show that the result of evaluation model of wedge stability based on blind data theory and Fisher optimal segmentation method is coincident with the generally accepted MCS method, which verifies the reliability and efficiency of the proposed method. The proposed method was applied to the stability evaluation of the wedge in Xingcheng to provide data support for the prevention and control of the wedge.
Key words: wedge uncertainty Fisher optimal segmentation blind data theory probability analysis Monte-Carlo simulation
秦胜伍, 马中骏, 陈骏骏, 吕江峰, 陈剑平, 曹荣国. 楔体稳定性概率分析方法及应用[J]. 哈尔滨工业大学学报, 2017, 49(12): 117-122. DOI: 10.11918/j.issn.0367-6234.201705028.
QIN Shengwu, MA Zhongjun, CHEN Junjun, LV Jiangfeng, CHEN Jianping, CAO Rongguo. Probability analysis method and application of wedge stability[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 117-122. DOI: 10.11918/j.issn.0367-6234.201705028.
基金项目 国家自然科学基金青年基金(41202197)；国家自然科学基金重点项目(41330636) 作者简介 秦胜伍(1980—)，男，副教授 通信作者 秦胜伍，qinsw@jlu.edu.cn 文章历史 收稿日期: 2017-05-05
Contents -->Abstract Full text Figures/Tables PDF
楔体稳定性概率分析方法及应用
秦胜伍
, 马中骏, 陈骏骏, 吕江峰, 陈剑平, 曹荣国 吉林大学 建设工程学院，长春 130026
收稿日期: 2017-05-05
基金项目: 国家自然科学基金青年基金(41202197)；国家自然科学基金重点项目(41330636)
作者简介: 秦胜伍(1980—)，男，副教授
通信作者: 秦胜伍，qinsw@jlu.edu.cn
摘要: 为综合分析参数具有多种不确定性的楔体的稳定性，提出一种基于Fisher最优分割法和盲数理论的楔体稳定性概率分析方法，该方法通过构造基于Fisher最优分割法的楔体稳定性盲数评价模型，综合考虑楔体参数的多种不确定性，确定楔体稳定性概率分布.文章构建了单滑面与双滑面的不确定性楔体稳定性盲数评价模型，将该模型应用于经典的双滑面楔体稳定性分析之中，并与传统的均值安全系数、数值模拟、蒙特卡洛抽样(MCS)方法的结果进行对比，结果表明：均值安全系数法和swedge数值分析只能给出一个固定的安全系数，准确度较低，不能考虑楔体的失稳概率，基于Fisher最优分割法和盲数理论的楔体稳定性分析方法安全系数累计频率与公认比较准确的蒙特卡洛抽样方法几乎重合，并且更加的高效简便，验证了该方法的可靠性与有效性.最后，将该方法应用于兴城某楔体的稳定性评价，为楔体的防治提供数据支撑.
关键词: 楔体 不确定性 Fisher最优分割 盲数理论 概率分析 蒙特卡洛模拟
Probability analysis method and application of wedge stability
QIN Shengwu
, MA Zhongjun, CHEN Junjun, LV Jiangfeng, CHEN Jianping, CAO Rongguo College of Construction Engineering, Jilin University, Changchun 130026, China
Abstract: To comprehensively analyze the wedge stability whose parameters have various uncertainties, a method was proposed to analyze the stability of wedge probability based on blind data theory and Fisher optimal segmentation method. A blind data evaluation model of wedge stability considering a variety of wedge parameter uncertainties was created to determine the wedge stability. The evaluation model of the blind number of the stability of the wedge was given, and the model was applied to the classical double-wedge stabilization, in which the result was compared with that from the traditional mean safety coefficient, numerical simulation, and Monte Carlo sampling (MCS). The compared results show that the result of evaluation model of wedge stability based on blind data theory and Fisher optimal segmentation method is coincident with the generally accepted MCS method, which verifies the reliability and efficiency of the proposed method. The proposed method was applied to the stability evaluation of the wedge in Xingcheng to provide data support for the prevention and control of the wedge.
Key words: wedge uncertainty Fisher optimal segmentation blind data theory probability analysis Monte-Carlo simulation
楔体破坏是岩质边坡最常见的破坏形式之一，它主要受控于岩体内部大量发育的不连续结构面[1-2].传统的楔体稳定性评价方法主要有均值安全系数法、数值分析法等，如极限平衡法[1-2]、Low和Einstein法[4]、有限元法[5]、离散元法[6]，但是此类方法在楔体稳定性分析过程中，块体中的各参数均被看作确定值，忽略了边坡岩土体参数如重度、内摩擦角、黏聚力等指标的多种不确定性，如模糊性、随机性、灰性、未确知性[7-8]等，将不确定性问题作为确定性问题考虑，然而，确定性定值分析方法难以反映影响楔体稳定性的各种因素的随机特性，不能全面表征楔体的实际安全状态.
目前，针对边坡岩土体参数的模糊性、随机性、灰性、未确知性，可以分别采用模糊数学、数理统计、灰色数学和未确知数学来分析处理[7]，对于考虑岩土体参数不确定性的楔体稳定性研究已取得一些研究成果，但都只是考虑了一种或者两种不确定性.如赵奎等[9]提出了块体稳定性的模糊随机可靠度分析方法，建立了块体稳定性的模糊概率测度计算公式；孙树林等[10]将随机概率模型引入到块体理论中，考虑楔体在几何参数和力学参数的随机分布下的破坏概率；孙立川等[11]研究了可靠度理论在岩质边坡楔体破坏反分析中的应用；王宇等[12]考虑了岩土体参数的随机性与模糊性，并提出了楔形体随机可靠分析改进的模糊点估计法.
盲数理论可以同时考虑参数的多种不确定性，基于此，本文将盲数理论和Fisher最优分割方法和运用于楔体稳定性分析之中，综合考虑楔体稳定性评价过程中岩土体参数的多种不确定性，建立了基于Fisher最优分割的不确定性楔体稳定性盲数评价模型，在此基础上，通过数值算例，并与传统方法以及相对精确的蒙特卡洛抽样方法(MCS)相对比，验证该模型的可靠性和高效性.
1 楔体稳定性盲数评价模型盲数是未确知数学中用于表达和处理同时具有两种或者两种以上不确定性信息的数学工具[8, 13-14]，通过盲数理论在处理不确定性问题时，在确定各盲数的概率分布密度函数时，需要人为的对有序排列的可能值序列进行聚类分割，具有很强的主观性.Fisher最优分割法[15-16]是一种对有序样本进行分割的方法，目标是让样本总体的离差平方和最小，原则上是让各类间的差异最大，各类内部的差异最小，可以在很大的程度上解决人为因素对可能值序列分组的问题.
1.1 模型构建采用均值安全系数或数值方法评价楔体稳定性时，参与计算的参数均为定值，忽略了计算公式中的各参数受地质条件、测量误差和施工人员素质等诸多因素影响的不确定性.为了克服传统确定性模型的缺陷，将盲数理论与Fisher最优分割法引入到楔体稳定性评价之中，构建基于Fisher最优分割法的不确定性楔体稳定性盲数评价模型，并进行楔体失稳概率分析.楔体评价模型构建的步骤见图 1.
Figure 1
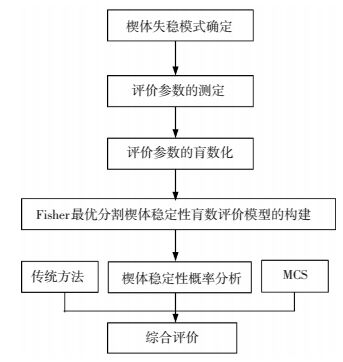图 1 基于Fisher最优分割法的楔体稳定性盲数评价模型构建流程图 Figure 1 Flowchart of wedge stability based on blind data theory and Fisher optimal segmentation method 1.2 楔体稳定性评价数学计算模型楔体是由两组结构面和临空面切割而成.如图 2所示，该楔体由结构面A和B、坡顶面、坡面组成[17]，其中，H为边坡高度，h为楔体高度，楔体上的作用力主要包括：楔体重力W，结构面A上的法向应力N1以及水压力U1，摩擦力F1，结构面B上的法向应力N2以及水压力U2，摩擦力F2.楔体常见的破坏形式有4种[17-18]：单面破坏(A面与B面)、双面破坏、漂浮破坏，其中漂浮破坏常出现在高孔隙水压力或高地应力地区.本文着重对单面破坏模式和双面破坏模式进行讨论.
Figure 2
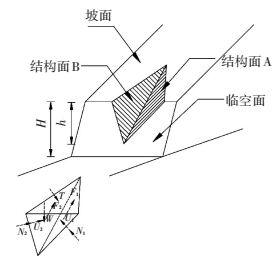图 2 楔体失稳几何模型 Figure 2 Slope geometry in wedge failure 1) 当楔体仅沿结构面A或者结构面B滑动时，其破坏模式为单面破坏，楔体的稳定性安全系数为
${F_{\rm{s}}} = \frac{{cA + N{\rm{tan}}\varphi }}{T},$ (1)
式中：c、A、φ分别为结构面的黏聚力、面积和内摩擦角，Fs为楔体的稳定性安全系数，
2) 当楔体滑动的过程中与两结构面均保持接触时，其破坏模式为双面破坏，楔体的稳定性安全系数为
${F_{\rm{s}}} = \frac{{{c_1}{A_1} + {c_2}{A_2} + {N_1}{\rm{tan}}{\varphi _1} + {N_2}{\rm{tan}}{\varphi _2}}}{S},$ (2)
$S = \left| {\overrightarrow R \cdot (\overrightarrow {{n_1}} \times \overrightarrow {{n_2}} )} \right|/\left| {(\overrightarrow {{n_1}} \times \overrightarrow {{n_2}} )} \right|.$ (3)
式中：c1、c2分别是结构面A与结构面B的黏聚力，A1、A2分别是结构面A与结构面B的面积，φ1、φ2分别是结构面A与结构面B的内摩擦角.
1.3 楔体稳定性盲数评价模型考虑边坡岩土体黏聚力c，内摩擦角φ均具有不确定性，故将这些参数用盲数进行表达，分别设为
$\left\{ {\begin{array}{*{20}{l}}{\tilde c = \{ [{c_{{\rm{min}}}},{c_{{\rm{max}}}}],{f_1}\left( c \right)\} ,}\\{\tilde \varphi = \{ [{\varphi _{{\rm{min}}}},{\varphi _{{\rm{max}}}}],{f_2}\left( \varphi \right)\} .}\end{array}} \right.$ (4)
式中：cmin、cmax分别为黏聚力c的下限和上限，f1(c)为c的盲数，φmin、φmax分别为φ的下限和上限，f2(φ)为φ的盲数.
1) 楔体单面破坏盲数计算模型为
${F_{\rm{s}}} = \frac{{\{ [{c_{{\rm{min}}}},{c_{{\rm{max}}}}],{f_1}\left( c \right)\} A + N{\rm{tan}}\{ [{\varphi _{{\rm{min}}}},{\varphi _{{\rm{max}}}}],{f_2}\left( \varphi \right)\} }}{T}.$ (5)
2) 楔体双面破坏盲数计算模型为
$\begin{array}{l}{F_{\rm{s}}} = (\{ [{c_{1{\rm{min}}}},{c_{1{\rm{max}}}}],{f_{11}}({c_1})\} {A_1} + \{ [{c_{2{\rm{min}}}},{c_{2{\rm{max}}}}],\\\quad \quad {f_{12}}({c_2})\} {A_2} + {N_1}{\rm{tan}}\{ [{\varphi _{1{\rm{min}}}},{\varphi _{1{\rm{max}}}}],{f_{21}}({\varphi _1})\} + \\\quad \quad {N_2}{\rm{tan}}\{ [{\varphi _{2{\rm{min}}}},{\varphi _{2{\rm{max}}}}],{f_{22}}({\varphi _2})\} )/S.\end{array}$ (6)
式中：f11(c1)与f12(c2)分别是结构面A与结构面B的c的盲数，f21(φ1)与f22(φ2)分别是结构面A与结构面B的φ的盲数.
2 算法验证为了验证本文方法的合理性以及有效性，选取了一个经典的岩质边坡楔体进行稳定性概率分析，该楔体首先为Hoek和Bray[18-19]所采用，通过对比本文模型计算结果与蒙特卡洛方法(MCS)、传统的均值安全系数方法，以及swedge数值分析的结果，来验证该方法的可靠性.
2.1 典型楔体楔体由结构面1与结构面2以及临空面切割而成，结构面及临空面描述见表 1，赤平投影见图 3.由于在天然状态下，结构面强度指标多数情况是服从正态分布的，所以利用计算机模拟了100组正态分布的结构面强度指标，即黏聚力c及内摩擦角φ.对岩土体c、φ数据进行统计分析，其统计特征值见表 2.图 4为两组节理面的黏聚力c以及内摩擦角φ分布直方图及其频数曲线，c1、c2、φ1、φ2均服从正态分布.
表 1
表 1 结构面及临空面描述 Table 1 The description of structure and surface 结构面倾向/(°)倾角/(°)粗糙度属性结构面110545平整裂隙面
结构面223570较粗糙层面
临空面18565H=33 m
坡顶面19512γ=25.2 kN/m3
表 1 结构面及临空面描述 Table 1 The description of structure and surface
Figure 3
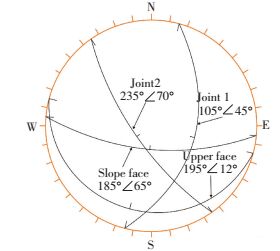图 3 楔体节理面及坡面赤平投影图 Figure 3 Stereonet projection of two joints and slope surface 表 2
表 2 参数统计特征值 Table 2 Statistical characteristics of parameters 岩土体参数平均值标准差上限值下限值c120.202.5832.1013.70
c250.143.6958.9038.90
φ119.784.3631.209.40
φ229.573.2640.9019.70
表 2 参数统计特征值 Table 2 Statistical characteristics of parameters
Figure 4
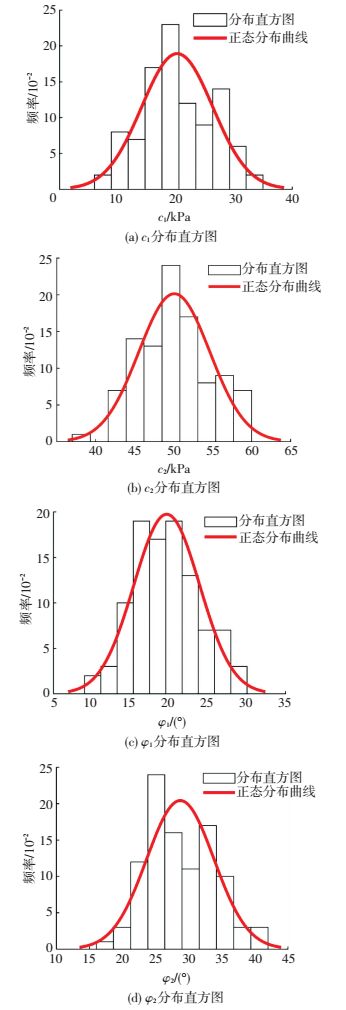图 4 黏聚力及内摩擦角分布直方图与密度曲线 Figure 4 Distribution histograms and probability density curves of cohesion and internal friction angle 2.2 基于Fisher最优分割的楔体盲数评价模型的构建1) 按照上文提到的模型构建方法构建楔体稳定性盲数评价模型，首先是判断其失稳类型，
${F_{\rm{s}}} = \frac{{{c_1}{A_1} + {c_2}{A_2} + {N_1}{\rm{tan}}{\varphi _1} + {N_2}{\rm{tan}}{\varphi _2}}}{S}.$ (7)
2) 运用盲数理论将表 2中的岩土体参数值定义为盲数，即为
3) 基于数学模型的盲数模型的建立，将强度参数的盲数表达式代入到式(7)中，即可得到该楔体的稳定性盲数评价模型，通过盲数运算法则和区间数运算法则得到该楔体的安全系数概率分布.得到的安全系数频率分布见图 5.
Figure 5
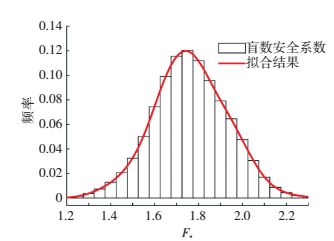图 5 盲数安全系数条形图 Figure 5 Probabilistic safety factor histogram of blind data theory 2.3 对比分析同时，对此楔体进行了另外3种传统方法的对比验算，其分别为均值安全系数法、swedge数值方法、蒙特卡洛抽样法.如图 6所示，为蒙特卡洛抽样方法进行107次抽样的结果，在此基础上，得到了盲数楔体评价模型、蒙特卡洛抽样方法累计频率分布图，如图 7所示.
Figure 6
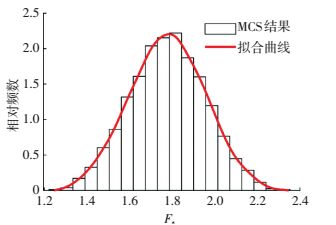图 6 蒙特卡洛方法安全系数条形图 Figure 6 Probabilistic safety factor histogram of Metro Carlo method Figure 7
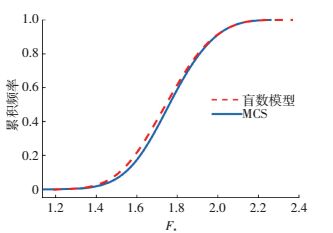图 7 两种方法累计频率图 Figure 7 Cumulative frequency diagram of the two methods 如表 3所示，对比几种方法可以发现，均值安全系数法和swedge模拟均只能给出一个固定的安全系数，准确度较低，基于Fisher最优分割法和盲数理论的楔体稳定性分析方法安全系数累计频率与公认比较准确的蒙特卡洛抽样方法几乎重合，同时，计算简单、快捷，验证了本文方法的可靠性与有效性.
表 3
表 3 各种方法对比 Table 3 Comparison of methods 方法安全系数准确度运算量均值安全系数1.757低低
Swedge模拟1.776低低
MCS见图 6高高
本文方法见图 5高低
表 3 各种方法对比 Table 3 Comparison of methods
3 工程应用研究楔体位于辽宁省兴城市，是一个废弃的采石场边坡，岩性主要为长城系大红裕组厚层石英砂岩，测量得楔体高45 m.由于该楔体为吉林大学等一大批高校的工程地质实习野外观测点，一旦发生楔体失稳，必然会造成无法挽回的损失.
2015年3月，在楔体现场进行了详细的工程地质调查并通过风钻、人工凿挖取样，结构面数据见表 4，通过蜡封法测定了岩石的密度，采用XJ-1型便携式剪切仪，系统地开展了室内的结构面直剪试验，测定的岩土体参数见表 5.由于岩土体参数的固有不确定性和试验数据样本有限引起的统计不确定性导致岩土体参数同时具有多种不确定性，对岩土体参数进行统计分析，通过KS检验，参数c1、c2、φ1、φ2均满足正态分布，其统计特征值见表 6.
表 4
表 4 结构面及临空面描述 Table 4 The description of structure and surface 结构面倾向/(°)倾角/(°)粗糙度属性结构面122.160.8平整层面
结构面2296.274.3较粗糙裂隙面
临空面11.672.6H=45 m
坡顶面34.512.3 γ=25 kN/m3
表 4 结构面及临空面描述 Table 4 The description of structure and surface
表 5
表 5 岩土体参数值 Table 5 Parameter values of rock and soil 试验编号黏聚力/kPa内摩擦角/(°)c1c2φ1φ2
1615123.432.2
2494231.227.9
3402527.131.1
4625927.730.0
5617528.230.4
6147429.534.1
7536423.228.8
8428816.226.6
9376726.927.6
10182927.531.8
11195831.132.2
12336125.632.9
13318523.227.5
表 5 岩土体参数值 Table 5 Parameter values of rock and soil
表 6
表 6 参数统计特征值 Table 6 Statistical characteristics of parameters 岩土体参数平均值标准差上限值下限值c140.016.7362.014.0
c259.919.4088.025.0
φ126.25.2431.216.2
φ230.22.4034.126.6
表 6 参数统计特征值 Table 6 Statistical characteristics of parameters
依据试验情况以及Fisher最优分割法对结构面的强度参数进行盲数表达为：
${{{\tilde{c}}}_{1}}=\left\{ \left[ 14,62 \right],{{f}_{11}}\left( {{c}_{1}} \right) \right\},{{{\tilde{c}}}_{2}}=\left\{ \left[ 25,88 \right],{{f}_{12}}\left( {{c}_{2}} \right) \right\},$
${{{\tilde{\varphi }}}_{1}}=\left\{ \left[ 16.2,31.2 \right],{{f}_{21}}\left( {{\varphi }_{1}} \right) \right\},{{{\tilde{\varphi }}}_{2}}=\left\{ \left[ 26.6,34.1 \right],{{f}_{22}}({{\varphi }_{2}}) \right\}.$
其中：
${f_{11}}({c_1}) = \left\{ {\begin{array}{*{20}{c}}{0.23} & {\left( {x \in \left[ {14 \sim 19} \right]} \right)}\\{0.54} & {\left( {x \in \left[ {31 \sim 53} \right]} \right)}\\{0.23} & {\left( {x \in \left[ {61 \sim 62} \right]} \right)}\\0 & {(x \in {\rm{others}})}\end{array}} \right.$
${f_{12}}({c_2}) = \left\{ {\begin{array}{*{20}{c}}{0.15} & {\left( {x \in \left[ {25 \sim 29} \right]} \right)}\\{0.70} & {\left( {x \in \left[ {42 \sim 75} \right]} \right)}\\{0.15} & {\left( {x \in \left[ {85 \sim 88} \right]} \right)}\\0 & {(x \in {\rm{others}})}\end{array}} \right.$
${f_{21}}({\varphi _1}) = \left\{ {\begin{array}{*{20}{c}}{0.15} & {\left( {x \in \left[ {16.2 \sim 18.2} \right]} \right)}\\{0.70} & {\left( {x \in \left[ {23.2 \sim 29.5} \right]} \right)}\\{0.15} & {\left( {x \in \left[ {31.1 \sim 31.2} \right]} \right)}\\0 & {(x \in {\rm{others}})}\end{array}} \right.$
${f_{22}}({\varphi _2}) = \left\{ {\begin{array}{*{20}{c}}{0.31} & {\left( {x \in \left[ {26.6 \sim 27.9} \right]} \right)}\\{0.54} & {\left( {x \in \left[ {28.8 \sim 32.2} \right]} \right)}\\{0.15} & {\left( {x \in \left[ {32.9 \sim 34.1} \right]} \right)}\\0 & {(x \in {\rm{others}})}\end{array}} \right.$
按文中所述方法构造不确定性楔体稳定性评价模型，并计算其安全系数盲数解，图 8为安全系数频率分布直方图.
Figure 8
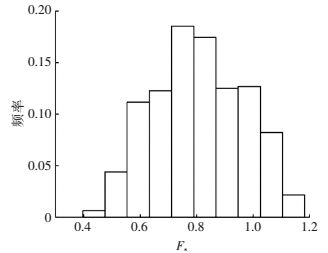图 8 盲数安全系数频率分布图 Figure 8 Probabilistic safety factor histogram of blind data theory 由图 8可知，该楔体安全系数低于1的概率为85.6%，低于1.2的概率为100%，失稳的可能性较大这一点与实际情况相吻合，在2015年6月，该楔体发生失稳，表明基于Fisher最优分割和盲数理论的楔体稳定性评价模型的可靠性与准确性.
4 结论1) 本文提出了一种基于Fisher最优分割的不确定性楔体稳定性盲数评价模型，该模型考虑了边坡岩土体参数的多种不确定性，克服了边坡岩土体参数多种不确定对于楔体稳定性分析影响，并且首次将Fisher最优分割法运用于盲数分组中，克服了人为因素的影响，能够更加客观全面地反映楔体的真实状态.
2) 算例表明，基于Fisher最优分割法与盲数理论的楔体稳定性概率分析方法计算结果与公认比较准确的蒙特卡洛方法相似，验证了本文方法的有效性与可靠性.
3) 以兴城某楔体作为研究对象，通过建立不确定性楔体稳定评价模型对楔体稳定性做出评价，为楔体的防治工程提供数据支撑.后续观测结果表明，该方法能够准确地评判楔体的稳定性.采用Fisher最优分割方法和盲数理论分析楔体的稳定性为岩土体稳定性分析提供了一个新的思路.
参考文献
[1]姜清辉, 刘献华, 位伟, 等. 岩质边坡楔体稳定分析与临界滑面搜索[J].岩石力学与工程学报, 2013, 32(1): 24-32.
JIANG Qinghui, LIU Xianhua, WEI Wei, et al. Wedge stability analysis for rock slope and search for critical slip surfaces[J].Chinese journal of Rock Mechanics and Engineering, 2013, 32(1): 24-32.
[2]PARK H J, UM J, WOO I, et al. The evaluation of the probability of rock wedge failure using the point estimate method[J].Environmental Earth Sciences, 2012, 65(1): 353-361.DOI: 10.1007/s12665-011-1096-7
[3]陈炜, 王均星, 辛丽萍, 等. 楔形体稳定的塑性极限分析下限法[J].岩土工程学报, 2009, 31(3): 431-436.
CHEN Wei, WANG Junxing, XIN Liping, et al. Lower bound method of plastic limit analysis for wedge stability[J].Chinese Journal of Geotechnical Engineering, 2009, 31(3): 431-436.
[4] LOW B K, EINSTEIN H H. Simplified reliability analysis for wedge mechanisms in rock slopes[C]// Proceedings of the 6th International Symposium on Landslides. New Zealand: Christchurch, 1992.
[5]陈菲, 邓建辉. 岩坡稳定的三维强度折减法分析[J].岩石力学与工程学报, 2006, 25(12): 2546-2551.
CHEN Fei, DENG Jianhui. Three-dimensional stability analysis of rock slope with strength reduction method[J].Chinese journal of Rock Mechanics and Engineering, 2006, 25(12): 2546-2551.DOI: 10.3321/j.issn:1000-6915.2006.12.022
[6]朱永生, 朱焕春, 石安池, 等. 基于离散单元法的白鹤滩水电站复杂块体稳定性分析[J].岩石力学与工程学报, 2011, 30(10): 2068-2075.
ZHU Yongsheng, ZHU Huanchun, SHI Anchi, et al. Complicated block stability analysis of baihetan hydropower station based on distinct element method[J].Chinese journal of Rock Mechanics and Engineering, 2011, 30(10): 2068-2075.
[7]陈训龙, 龚文惠, 邱金伟, 等. 基于盲数理论的边坡可靠度分析[J].岩石力学与工程学报, 2016, 35(6): 1-6.
CHEN Xunlong, GONG Wenhui, QIU Jinwei, et al. Reliability analysis of slope based on blind data theory[J].Chinese journal of Rock Mechanics and Engineering, 2016, 35(6): 1-6.
[8]董陇军, 李夕兵. 岩石试验抗压?抗拉区间强度及代表值可信度研究[J].岩土工程学报, 2010, 32(12): 1969-1974.
DONG Longjun, LI Xibing. Interval parameters and credibility of representative values of tensile and compression strength tests on rock[J].Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1969-1974.
[9]赵奎, 蔡美峰, 饶运章, 等. 采空区块体稳定性的模糊随机可靠性研究[J].岩土力学, 2003, 24(6): 987-990.
ZHAO Kui, CAI Meifeng, RAO Yunzhang, et al. Study on fuzzy random reliability analysis for block stability in caved area[J].Rock and Soil Mechanics, 2003, 24(6): 987-990.
[10]孙树林, 朱杰. 节理化岩质边坡的关键块体可靠度分析[J].岩石力学与工程学报, 2007, 26(1): 131-136.
SUN Shulin, ZHU Jie. Reliability analysis of key block for a jointed rock slope[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 131-136.
[11]孙立川, 王红贤, 周念清, 等. 可靠度理论在岩质边坡楔形体破坏反分析中的应用[J].岩石力学与工程学报, 2012, 31(S1): 2660-2667.
SUN Lichuan, WANG Hongxian, ZHOU Nianqing, et al. Application of reliability theory to back analysis of rocky slope wedge failure[J].Chinese journal of Rock Mechanics and Engineering, 2012, 31(S1): 2660-2667.
[12]王宇, 魏献忠, 黎明, 等. 岩质边坡楔形体稳定模糊随机可靠性研究[J].地质科技情报, 2012, 31(4): 111-116.
WANG Yu, WEI Xianzhong, LI Ming, et al. Wedge analysis for rock mass slope base on fuzzy random theory[J].Geological Science and Technology Information, 2012, 31(4): 111-116.
[13]刘开第, 吴和琴, 庞彦军, 等. 不确定性信息数学处理及应用[M]. 北京: 科学出版社, 1999.
LIU Kaidi, WU Heqin, PANG Yanjun, et al. Mathematics treatment and application of uncertainty information[M]. Beijing: Science Press, 1999.
[14]李如忠, 范传勇. 基于盲数理论的河流水环境容量计算[J].哈尔滨工业大学学报, 2009, 41(10): 233-235.
LI Ruzhong, FAN Chuanyong. Calculation on carrying capacity of river water[J].Journal of Harbin Institute of Technology, 2009, 41(10): 233-235.DOI: 10.3321/j.issn:0367-6234.2009.10.051
[15]FISHEER W D. On grouping for maximum homogeneity[J].Journal of the American Statistical Association, 1958, 53(284): 789-798.DOI: 10.2307/2281952
[16]高峰, 刘江, 杨新刚, 等. 基于Fisher最优分割法的机床热关键点优化研究[J].仪器仪表学报, 2013, 34(5): 1070-1075.
GAO Feng, LIU Jiang, YANG Xin'gang, et al. Study on optimization of thermal key points for machine tools based on Fisher optimal segmentation method[J].Chinese Journal of Scientific Instrument, 2013, 34(5): 1070-1075.
[17]JIANG Q, LIU X, WEI W, et al. A new method for analyzing the stability of rock wedges[J].International Journal of Rock Mechanics and Mining Sciences, 2013, 60(8): 413-422.DOI: 10.1016/j.ijrmms.2013.01.008
[18]HOEK E T, BRAY J W. Rock slope engineering[M]. 3rd ed. London: Institute of Mining and Metallurgy, 1981.
[19]LI D, ZHOU C, LU W, et al. A system reliability approach for evaluating stability of rock wedges with correlated failure modes[J].Computers and Geotechnics, 2009, 36(8): 1298-1307.DOI: 10.1016/j.compgeo.2009.05.013
