脉冲干扰时滞复值神经网络的稳定性分析

徐晓惠¹, 张继业², 施继忠³, 任松涛¹

(1.西华大学 汽车与交通学院,610039 成都;2. 牵引动力国家重点实验室(西南交通大学),610031 成都; 3.浙江师范大学 工学院, 321004 浙江 金华)



摘要:

为分析脉冲干扰因素对复值神经网络动态行为的影响，研究一类具有混合时滞和脉冲干扰的复值神经网络的平衡点的全局指数稳定性.在假定神经元状态、激活函数以及关联矩阵定义在复数域的情况下，利用M矩阵理论、向量Lyapunov函数法以及数学归纳法，分析确保该系统平衡点的存在性、唯一性以及全局指数稳定性的充分条件，并给出了指数收敛率，最后通过一个数值仿真算例验证了所得结论的正确性.结果表明：时滞和脉冲干扰均会降低神经元状态的指数收敛速度，所建立的稳定性判据推广了现有结论.

关键词:  复值神经网络  脉冲干扰  混合时滞  全局指数稳定性  矢量Lyapunov函数

DOI：10.11918/j.issn.0367-6234.2016.03.028

分类号:TP391

文献标识码:A

基金项目:国家自然科学基金(4,2, 4,1)；四川省青年科技创新研究团队专项计划 (2015TD0021)；教育部“春晖计划”合作科研项目(Z2014075)；浙江省自然科学基金(LY14E08006).



Stability analysis of delayed complex-valued neural networks with impulsive disturbances

XU Xiaohui¹, ZHANG Jiye², SHI Jizhong³, REN Songtao¹

(1.School of Automobile and Transportation, Xihua University, 610039 Chengdu, China; 2.National Traction Power Laboratory（Southwest Jiaotong University）, 610031 Chengdu, China; 3. College of Engineering, Zhejiang Normal University, 321004 Jinhua, Zhejiang,China)

Abstract:

To investigate the effect of impulsive disturbances on the dynamical behavior of the equilibrium point of complex-valued neural networks, the globally exponential stability of a class of the system with mixed delays and impulsive disturbances was studied in this paper. Assume that the neuron states, activation functions and interconnected matrix were defined in the complex domain. Some sufficient conditions for assuring the existence, uniqueness and globally exponential stability of the equilibrium point of the system were obtained by applying the M matrix theory, the mathematical induction and the vector Lyapunov function methods. Meanwhile, the exponential convergence rate was proposed. It can be concluded from the established sufficient conditions that the exponential convergence rate of the neurons is reduced by both time delays and the impulsive disturbances. The stability criteria established in this paper generalize the existing results. Finally, a numerical example with simulations was given to show the correctness of the obtained results.

Key words:  complex-valued neural networks  impulsive disturbances  mixed delays  globally exponential stability  vector Lyapunov function


徐晓惠, 张继业, 施继忠, 任松涛. 脉冲干扰时滞复值神经网络的稳定性分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 166-170. DOI: 10.11918/j.issn.0367-6234.2016.03.028.
XU Xiaohui, ZHANG Jiye, SHI Jizhong, REN Songtao. Stability analysis of delayed complex-valued neural networks with impulsive disturbances[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 166-170. DOI: 10.11918/j.issn.0367-6234.2016.03.028.
基金项目 国家自然科学基金（11402214，51375402，11572264，61273021）；四川省青年科技创新研究团队专项计划（2015TD0021）；教育部"春晖计划"合作科研项目（Z2014075）；浙江省自然科学基金（LY14E08006） 作者简介 徐晓惠(1982-), 女, 副教授;
张继业(1965-), 男, 教授, 博士生导师 通信作者 徐晓惠, xhxu@163.com 文章历史 收稿日期: 2014-12-10



Contents            -->Abstract            Full text            Figures/Tables            PDF


脉冲干扰时滞复值神经网络的稳定性分析
徐晓惠¹, 张继业², 施继忠³, 任松涛¹    
1. 西华大学 汽车与交通学院, 610039 成都;
2. 牵引动力国家重点实验室(西南交通大学), 610031 成都;
3. 浙江师范大学 工学院, 321004 浙江 金华

收稿日期: 2014-12-10
基金项目: 国家自然科学基金（11402214，51375402，11572264，61273021）；四川省青年科技创新研究团队专项计划（2015TD0021）；教育部"春晖计划"合作科研项目（Z2014075）；浙江省自然科学基金（LY14E08006）
作者简介: 徐晓惠(1982-), 女, 副教授;
张继业(1965-), 男, 教授, 博士生导师
通信作者: 徐晓惠, xhxu@163.com


摘要: 为分析脉冲干扰因素对复值神经网络动态行为的影响，研究一类具有混合时滞和脉冲干扰的复值神经网络的平衡点的全局指数稳定性.在假定神经元状态、激活函数以及关联矩阵定义在复数域的情况下，利用M矩阵理论、向量Lyapunov函数法以及数学归纳法，分析确保该系统平衡点的存在性、唯一性以及全局指数稳定性的充分条件，并给出了指数收敛率，最后通过一个数值仿真算例验证了所得结论的正确性.结果表明：时滞和脉冲干扰均会降低神经元状态的指数收敛速度，所建立的稳定性判据推广了现有结论.
关键词: 复值神经网络    脉冲干扰    混合时滞    全局指数稳定性    矢量Lyapunov函数    
Stability analysis of delayed complex-valued neural networks with impulsive disturbances
XU Xiaohui¹, ZHANG Jiye², SHI Jizhong³, REN Songtao¹    
1. School of Automobile and Transportation, Xihua University, 610039 Chengdu, China;
2. National Traction Power Laboratory(Southwest Jiaotong University), 610031 Chengdu, China;
3. College of Engineering, Zhejiang Normal University, 321004 Jinhua, Zhejiang, China


Abstract: To investigate the effect of impulsive disturbances on the dynamical behavior of the equilibrium point of complex-valued neural networks, the globally exponential stability of a class of the system with mixed delays and impulsive disturbances was studied in this paper. Assume that the neuron states, activation functions and interconnected matrix were defined in the complex domain. Some sufficient conditions for assuring the existence, uniqueness and globally exponential stability of the equilibrium point of the system were obtained by applying the M matrix theory, the mathematical induction and the vector Lyapunov function methods. Meanwhile, the exponential convergence rate was proposed. It can be concluded from the established sufficient conditions that the exponential convergence rate of the neurons is reduced by both time delays and the impulsive disturbances. The stability criteria established in this paper generalize the existing results. Finally, a numerical example with simulations was given to show the correctness of the obtained results.
Keywords: complex-valued neural networks    impulsive disturbances    mixed delays    globally exponential stability    vector Lyapunov function    
近年来，复值神经网络在联想记忆^[1]、模式识别^[2]、优化问题求解^[3]等领域得到了越来越多的应用，关于复值神经网络的其他应用参见文献[4].神经网络平衡点的存在性以及收敛性是将其进行硬件设计的前提条件，因此对复值神经网络平衡点的动力学行为的研究是非常必要的.文献[5]研究了一类具有固定时滞的递归复值神经网络，并利用LMI方法给出了判定该系统全局稳定的充分条件.文献[6]研究了一类离散复值神经网络，并给出了判定平衡点存在性、唯一性和指数稳定的判定定理.文献[7]在假设复值激活函数关于神经元状态分别满足有界或Lipschitz条件的情况下，利用LMI方法研究了一类具有固定时滞的复值神经网络平衡点的动态行为.文献[8]研究了一类递归复值神经网络的多稳态问题，但在模型中没有考虑时滞.时滞现象在实际系统中是不可避免的, 在神经网络中引入时间滞后参量，有利于移动目标的图像处理、移动物体速度的确定和模式分类.文献[9-10]在研究一类复值神经网络平衡点的多稳态问题时在模型中引入了时滞，并得到了相应的稳定性充分判据.文献[11-12]也初步研究了几类具有混合时滞的复值神经网络的平衡点的动态行为，并利用向量Lyapunov函数法的得到了确保系统平衡点存在性、唯一性以及指数稳定性的充分判据.文献[5-12]所考虑的复值神经网络都是确定型系统，在实现复值神经网络硬件系统中，由于频率转换或者开关闭合等操作，使得系统的状态在某些离散时刻会发生瞬间跳变，即系统状态受到脉冲干扰.关于具有脉冲干扰的实值神经网络的动态行为分析，文献[13-17]已经作了大量的研究，然而目前尚未有学者对具有脉冲干扰的混合时滞复值神经网络平衡点的动态行为进行过相关研究.基于以上分析，本文将在一类复值神经网络模型中同时考虑混合时滞和脉冲干扰，利用向量Lyapunov函数法和数学归纳法，研究该系统平衡点的模的全局指数稳定性，并得到确保系统全局指数稳定的充分条件.

1 模型描述、基本假设以及引理首先定义一些记号.令 C 为复数域，R 为实数域.记 z=x+yi∈C，|z|=(x²+y²)^0.5 为复数 z 的模，且 z^* 为 z 的共轭转置.对于复数向量 z∈Cⁿ，令|z|=(|z₁|, |z₂|, …, |z_n|)^T，定义‖z‖= . 对于复数矩阵 A=(a_kj)_n×n∈C^n×n，A^* 为矩阵 A 的共轭转置矩阵.考虑如下具有脉冲干扰的混合时滞复值神经网络:

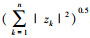
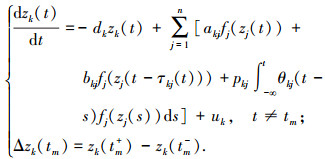(1)

其中：z_k∈C 为第 k 个神经元状态，k=1, 2, …, n，m∈Ν，n 为神经元个数；Δz_k(t_m) 为在离散时刻 t_m 系统状态的突变量，离散集{ t_m }满足 0≤t₀＜t₁＜…＜t_m＜…，且当 m→∞ 时 t_m→∞，假设 z_k(t_m)=z_k(t_m⁺) 且；A=(a_kj)_n×n∈C^n×n，B=(b_kj)_n×n∈C^n×n 和 P=(p_kj)_n×n∈C^n×n 分别为该系统的关联矩阵；U=(u₁, u₂, …, u_n)^T∈Cⁿ 为系统外部常输入；f(z(t))=(f₁(z₁(t)), f₂(z₂(t)), …, f_n(z_n(t)))^T 为该系统的激活函数，D=diag(d₁, d₂, …, d_n)∈R^n×n 为自反馈关联矩阵，且 d_k>0 ，k=1, 2, …, n；时延 τ_kj(t)(k, j=1, 2, …, n) 为有界函数，且 τ=max_{1≤k, j≤n}sup_t≥0τ_kj(t).

假设连续函数 θ_kj：[0, +∞)→[0, +∞)，满足

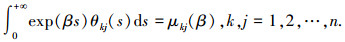(2)

其中：μ_kj(β) 为 [0, δ) 上的连续函数，且 μ_kj(0)=1，这里 δ>0.

假设系统(1)的初始条件为 z_k(s)=φ_k(s) ，其中 φ_k(s) 为 (－∞, 0] 上的有界连续函数.令 z^#=(z₁^#, z₂^#, …, z_n^#)^T 为系统(1)的平衡点.

定义1??若存在常数 Γ>0 和 λ>0，对所有 U∈Cⁿ 及 t≥0，有 ‖z(t)－z^#‖≤sup_{s∈(－∞, 0]}‖φ(s)－z^#‖Γexp(－λt) 成立，则称系统(1)的平衡点 z^# 是全局指数稳定的.

假设1??假设激活函数 f_k(·) 满足全局Lipschitz条件，即存在Lipschitz常数 l_k>0，使得对所有 z_k, v_k∈C，有 |f_k(z_k)－f_k(v_k)|≤l_k|z_k－v_k| 成立，k=1, 2, …, n. 令 L=diag(l₁, l₂, …, l_n).

假设2??令 Δz_k(t_m)=z_k(t_m⁺)－z_k(t_m^－)=I_km(z_k(t_m^－))，其中 I_km(·) 为复值连续脉冲函数，且 I_km(0)=0. 假设存在常数 η_km>0，使得不等式 |z_k(t_m^－)+I_km(z_k(t_m^－))|≤η_km|z_k(t_m^－)| 成立，k=1, 2, …, n，m∈Ν. 令 η_m=max{1, η_1m, η_2m, …, η_nm}.

引理1^[11]??对于矩阵 A=(a_kj)_n×n∈R^n×n，如果所有非对角元素 a_kj≤0，k≠j，则下面陈述是等价成立的：a) A为M矩阵；b) A 的各阶顺序主子式均为正；c)存在 ξ∈Rⁿ>0，使得 Aξ>0；d) A 的所有特征根的实部为正.

2 主要结论定理1??假设1、2是成立的.若存在常数 λ>0 和 η>0，其中 且满足 λ>η，以及一系列正常数 ξ_k 使得下面的不等式均成立.

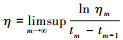
(3)

这里 k=1, 2, …, n, m∈N. 那么系统(1)针对任意外部常输入 U∈Cⁿ，均存在唯一平衡点 z^#，且该平衡点是全局指数稳定的，指数收敛率为 0.5(λ－η).

证明??令，则系统(1)可改写为

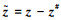
(4)

其中.

令系统(4)的初始条件为 ψ_k(s)=φ_k(s)－z_k^#，k=1, 2, …, n，－∞＜s≤0. 考虑到不等式(3)以及引理1可知矩阵 Q 为M矩阵，且



其中 k, j=1, 2, …, n 且 k≠j.

根据文献[11]中定理1可知，系统(1)的连续部分存在唯一平衡点 z^#，即系统(4)存在唯一平衡点. 选择如下向量Lyapunov函数:



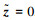
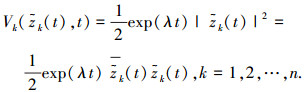
在不引起混淆的情况下，将 记作 V_k(t)，k=1, 2, …, n. 当 0 < t < t₁ 时，计算 V_k(t) 沿方程(4)的右上导数，并考虑到假设1，有

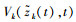
(5)

定义曲线 ζ={ω(χ):ω_k=ξ_kχ, χ＞0, k=1, 2, …, n} 和集合 Ω(ω)={h:0≤h≤ω, ω∈ζ}. 显然当 χ＞χ^′，Ω(ω(χ)) Ω(ω(χ′)). 令 ξ_max=max_1≤k≤n{ξ_k}，ξ_min=min_1≤k≤n{ξ_k}，χ₀=δ‖ψ‖²/ξ_min，其中 δ>1 为一个常数，则

Ω(ω₀(χ₀))，即.

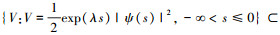
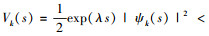
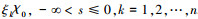
进一步可得 V_k(t) < ξ_kχ₀，k=1, 2, …, n，0 < t < t₁. 若该不等式不成立，那么存在某个 k 和时刻 t^*(0 < t^* < t₁)，使得 V_k(t^*)=ξ_kχ₀，D⁺V_k(t^*)≥0，V_j(t^*)≤ξ_jχ₀，j=1, 2, …, n. 将其代入到不等式(5)中，并考虑到不等式(3)，有



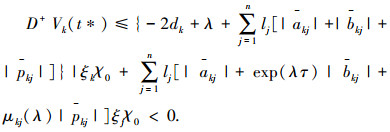
这与假设 D⁺V_k(t*)≥0 是矛盾的.因此有 V_k(t) < ξ_kχ₀，即|z_k(t)| < (2ξ_kχ₀exp(－λt))^0.5，k=1, 2, …, n，0 < t < t₁.

接下来，采用数学归纳法证明:

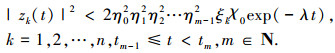(6)

当 m=1 时，|z_k(t)|² < 2η₀ξ_kχ₀exp(－λt)，k=1, 2, …, n，t₀≤t＜t₁，其中 η₀=1. 根据上面的分析，该式显然成立.假设下面的不等式是成立的，即

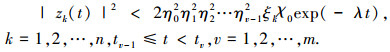(7)

当 t=t_m 时，根据假设2有 |z_k(t_m⁺)|²=|z_k(t_m^－)+I_km(z_k(t_m^－))|²≤η_km²|z_k(t_m^－)|²≤η_m²|z_k(t_m^－)|².

由于 η_m≥1，进而不等式(7)变为

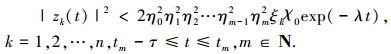(8)

进一步可以得到下面的不等式成立，即

(9)

若上式不成立，那么存在某个子系统 k′ 和时刻 t′，使得 D⁺V_k′(t′)≥0 以及



然后将其代入到式(5)中, 并考虑到式(3)，有



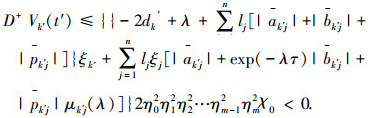
这与假设 D⁺V_k′(t′)≥0 是矛盾的.因此不等式(9)是成立的.根据数学归纳法，有

(10)

根据定理条件, 可知 η_m≤exp(0.5η(t_m－t_m－1))，即 η_m²≤exp(η(t_m－t_m－1))，m∈Ν. 将其代入到不等式(10)中，有



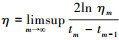
进一步，有

‖z(t)‖＜(2δ‖ψ‖²ξ_max/ξ_min)^0.5exp(－0.5(λ－η)(t－t₀))=Γ‖ψ‖exp(－0.5(λ－η)(t－t₀))，其中 Γ=(2δξ_max/ξ_min)^0.5.

根据定义1可知系统(4)的零解是全局指数稳定的，也就是说系统(1)的平衡点 z^# 是全局指数稳定的，且指数收敛率为 0.5(λ－η). 证毕.

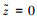
通过定理1所建立的稳定性判据，可得出如下结论：1)对于系统(1)，当系统中没有脉冲干扰因素时，该模型与文献[11]中所研究的模型是相同的.判定该系统平衡点的存在性、唯一性以及全局指数稳定性的充分条件是假设1成立且矩阵 Q 为M矩阵.该结论即为文献[11]中的定理1和定理2.本文所建立的判据推广了现有结论. 2)文献[5, 8, 10-11]以及文献[7]中的定理2在研究各类复值神经网络的动态行为时，继续沿用了分析实值神经网络动态行为的方法，即采用了将复值神经网络系统分解成实部系统和虚部系统的方法，得到了确保系统实部状态和虚部状态稳定的充分判据.本文在研究该复值系统时，并没有对系统进行实部与虚部的拆分，所建立的稳定性判据为神经元状态的模的全局指数稳定性.此外，文献[9]和文献[7]中定理3也给出了判定一类复值神经网络系统神经元状态的模的稳定性的充分条件，但在系统模型中未考虑无穷时滞和脉冲干扰因素. 3)当系统(1)中仅含有可变时滞或者无穷时滞时，令定理1的不等式条件(3)中的 b_kj=0 或 p_kj=0，其中 k, j=1, 2, …, n，其他假设条件不变，便可得到确保相应系统平衡点全局指数稳定的充分条件.

3 算例考虑如下复值神经网络

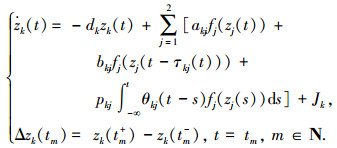(11)

其中 z₁(t)=x₁(t)+y₁(t)i，z₂(t)=x₂(t)+y₂(t)i.

假设已知自反馈矩阵.

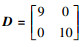
加权矩阵分别为



激活函数为



脉冲发生时刻为 {0.2 s, 0.4 s, 0.6 s, 0.8 s, …}，且



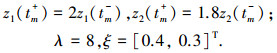
经计算，有 l₁=0.50，l₂=0.25，η=6.93.



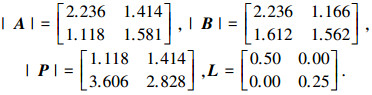
令系统(11)中的时延为 τ_1j=0.025－0.015sin t，τ_2j=0.03－0.01cos t，j=1, 2，t≥0. 令



令初始条件为



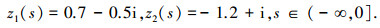
进一步计算有



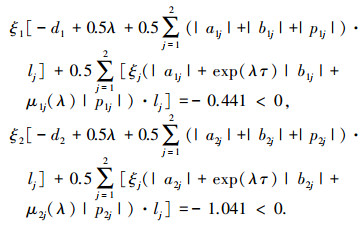
根据定理1可得结论：系统(11)存在唯一平衡点，且该平衡点是指数稳定的，指数收敛率为0.535.关于系统(11)的仿真结果见图 1、2，仿真结果验证了以上结论.

Figure 1
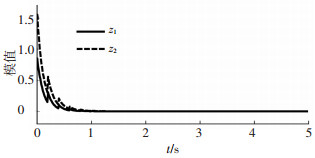图 1 系统(11)状态的模曲线


Figure 2
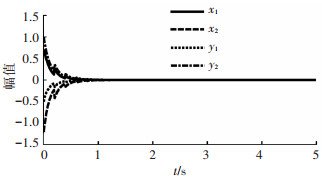图 2 系统(11)状态的实部曲线和虚部曲线


4 结论1) 针对一类具有脉冲干扰的混合时滞复值神经网络，在没有沿用实值神经网络研究方法的情况下，对其平衡点的模的全局指数稳定性进行分析.利用M矩阵理论、向量Lyapunov函数法以及数学归纳法，得到了确保该系统平衡点的模全局指数稳定性的充分条件.

2) 稳定性判据同时显示出了时滞和脉冲干扰对系统平衡点指数收敛速度的影响，即时滞越大，脉冲干扰越强烈，系统神经元状态收敛的速度越慢.所取得的研究成果推广了现有结论.

3) 通过数值算例验证了得的结论的可行性，同时算例仿真结果也显示该结论的正确性.


参考文献
[1] LEE D L. Improvement of complex-valued Hopfield associative memory by using generalized projection rules[J]. IEEE Transactions on Neural Networks, 2006, 17(5): 1341-1347. DOI:10.1109/TNN.2006.878786


[2] NAIT-CHARIF H. Complex-valued neural networks fault tolerance in pattern classification applications[C]//Proceedings of the Second WRI Global Congress on Intelligent Systems. Wuhan: IEEE, 2010: 154-157. https://ieeexplore.ieee.org/document/5709345/


[3] JIANG D. Complex-valued recurrent neural networks for global optimization of beamforming in multi-symbol MIMO communication systems[C]//Proceedings of International Conference on Conceptual Structurtion. Shanghai: Springer, 2008: 1-8.


[4] HIROSE A. Recent progress in applications of complex-valued neural networks[C]//Proceedings of 10th International Conference on Artificiality Intelligence Soft Computing Ⅱ. Zakopane: Springer, 2010: 42-46. https://link.springer.com/chapter/10.1007/978-3-642-13232-2_6


[5] ZHANG Ziye, LIN Chong, CHEN Bing. Global stability criterion for delayed complex-valued recurrent neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(9): 1704-1708. DOI:10.1109/TNNLS.2013.2288943


[6] SREE H, MURTHY G. Global dynamics of a class of complex valued neural networks[J]. International Journal Neural Systems, 2008, 18(2): 165-171. DOI:10.1142/S0129065708001476


[7] HU Jin, WANG Jun. Global stability of complex-valued recurrent neural networks with time-delays[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(6): 853-864. DOI:10.1109/TNNLS.2012.2195028


[8] HUANG Yujiao, ZHANG Huaguang, WANG Zhanshan. Multistability of complex-valued recurrent neural networks with real-imaginary-type activation functions[J]. Applied Mathematics and Computation, 2014, 229: 187-200. DOI:10.1016/j.amc.2013.12.027


[9] ZHAO Zhenjiang, SONG Qiankun. Global exponential stability of complex-valued neural networks with time-varying delays on time scales[C]//Proceedings of the 33rd Chinese Control Conference. Nanjing: Control Systems IEEE, 2014: 5080-5085.


[10] ZHOU Bo, SONG Qiankun. Boundedness and complete stability of complex-valued neural networks with time delay[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(8): 1227-1238. DOI:10.1109/TNNLS.2013.2247626


[11] 徐晓惠, 张继业, 赵玲. 一类混合时滞复值神经网络的动态行为分析[J]. 西南交通大学学报, 2014, 49(3): 470-476.


[12] XU Xiaohui, ZHANG Jiye, SHI Jizhong. Exponential stability of complex-valued neural networks with mixed delays[J]. Neurocomputing, 2014, 128: 483-490. DOI:10.1016/j.neucom.2013.08.014


[13] SONG Qiankun, ZHANG Jiye. Global exponential stability of impulsive Cohen-Grossberg neural network with time-varying delays[J]. Nonlinear Analysis:Real World Applications, 2008, 9(2): 500-510. DOI:10.1016/j.nonrwa.2006.11.015


[14] LI Liangliang, JIAN Jigui. Exponential convergence and Lagrange stability for impulsive Cohen-Grossberg neural networks with time-varying delays[J]. Journal of Computational and Applied Mathematics, 2015, 277: 23-35. DOI:10.1016/j.cam.2014.08.029


[15] TOJTOVSKA B, JANKOVIC S. On some stability problems of impulsive stochastic Cohen-Grossberg neural networks with mixed time delays[J]. Applied Mathematics and Computation, 2014, 239: 211-226. DOI:10.1016/j.amc.2014.04.038


[16] 杨治国, 黄玉梅. 具有混合时滞的脉冲Cohen-grossberg神经网络的指数耗散性[J]. 四川大学学报(自然科学版), 2010, 47(3): 464-468.


[17] 施继忠, 徐晓惠, 张继业. 扩散反应脉冲Cohen-Grossberg神经网络的鲁棒稳定性[J]. 西南交通大学学报, 2010, 45(4): 596-602.