Vibration and Acoustic Response of Sandwich Panels with Flexible Core Under Thermal Environments

Jingyong Han^1,2, Kaiping Yu¹, Haiyang Song¹and Xiangyang Li¹

(1.School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;2. China Academy of Launch Vehicle Technology, Beijing 100076, China)



Abstract:

Sandwich panels are increasingly used in the aerospace industry in recent years. Aircrafts are always affected by the thermal and noise environment during their life in service. Analytical studies on the sound vibration response of the sandwich panels with flexible core under thermal environments are performed in the paper. Governing equations are obtained by applying Hamilton’s principle with both anti-symmetric and symmetric motions taken into consideration. Natural frequencies, mode shape and critical temperature are acquired with thermal stresses considered. The forced vibration response and sound radiation are obtained based on the mode superposition principle and the Rayleigh integral. The model is validated compared with the results in literature. Natural frequencies for both anti-symmetric and symmetric motions decrease with temperature rise. Lower order flexural mode and higher-order dilatational mode are sensitive to the temperature change. Symmetric motion induces the anti-resonance frequencies move to the low frequency range. The peaks of sound vibration response remove to the low frequency range as the temperature rise and the amplitude of the peaks decrease due to the enhanced damping.The proposed model may serve as an effective guideline for the application of sandwich panels in thermal environments.

Key words:  sandwich panels  symmetric motion  vibration  sound radiation  thermal environment

DOI：10.11916/j.issn.1005-9113.16055

Clc Number:TB532

Fund:


Jingyong Han, Kaiping Yu, Haiyang Song, Xiangyang Li. Vibration and Acoustic Response of Sandwich Panels with Flexible Core Under Thermal Environments[J]. Journal of Harbin Institute of Technology, 2017, 24(5): 20-31. DOI: 10.11916/j.issn.1005-9113.16055.
Fund Sponsored by the National Natural Science Foundation of China (Grant No. 11372084) Corresponding author Kaiping Yu, E-mail: yukp@hit.edu.cn Article history Received: 2016-02-24



Contents            Abstract            Full text            Figures/Tables            PDF


Vibration and Acoustic Response of Sandwich Panels with Flexible Core Under Thermal Environments
Jingyong Han^1,2, Kaiping Yu¹, Haiyang Song¹, Xiangyang Li¹    
1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;
2. China Academy of Launch Vehicle Technology, Beijing 100076, China

Received: 2016-02-24
Fund: Sponsored by the National Natural Science Foundation of China (Grant No. 11372084)
Corresponding author: Kaiping Yu, E-mail: yukp@hit.edu.cn


Abstract: Sandwich panels are increasingly used in the aerospace industry in recent years. Aircrafts are always affected by the thermal and noise environment during their life in service. Analytical studies on the sound vibration response of the sandwich panels with flexible core under thermal environments are performed in the paper. Governing equations are obtained by applying Hamilton's principle with both anti-symmetric and symmetric motions taken into consideration. Natural frequencies, mode shape and critical temperature are acquired with thermal stresses considered. The forced vibration response and sound radiation are obtained based on the mode superposition principle and the Rayleigh integral. The model is validated compared with the results in literature. Natural frequencies for both anti-symmetric and symmetric motions decrease with temperature rise. Lower order flexural mode and higher-order dilatational mode are sensitive to the temperature change. Symmetric motion induces the anti-resonance frequencies move to the low frequency range. The peaks of sound vibration response remove to the low frequency range as the temperature rise and the amplitude of the peaks decrease due to the enhanced damping.The proposed model may serve as an effective guideline for the application of sandwich panels in thermal environments.
Key words: sandwich panels    symmetric motion    vibration    sound radiation    thermal environment    
1 IntroductionSandwich panels have been extensively used in the field of aerospace where the thermal environment is a critical factor to the structures throughout their service life. Thermal stresses due to the thermal environment can alter the sound vibration characteristics of the sandwich panels. A thorough understanding of the dynamic characters is imperative for designers to suppress the vibration and sound radiation of the sandwich panels.

The research on modeling of the sandwich panels has received considerable attention in literatures for quite a long time. Sayyad and Ghugal^[1] reviewed different methods for the free vibration analysis of multilayered laminated composite and sandwich panels, in which 391 references were cited. Frostig^[2-3] proposed a general high-order theory to investigate the buckling and static bending behavior of sandwich panels with transverse flexible core. Applying various methods, they also studied the free vibration of the unidirectional sandwich panels with both compressible and incompressible core^[4-5]. Oskooei and Hansen^[6] and Nabarrete et al.^[7] formulated a high-order finite element in which the core displacement fields are parabolic and cubic for the static and vibration analysis of sandwich panels. Frostig and Thomsen^[8] developed two sorts of computational models with different variables to deal with free vibration of the sandwich panels with flexible core which takes the core compressibility into consideration. Elmalich and Rabinovitch^[9] investigated the vibration behavior of soft-core sandwich panels by employing a higher-order finite element which considered the compressibility of the core. The accuracy of the FE method was confirmed by comparing with the theoretical results derived by Frostig and Thomsen^[8].

Meanwhile, research on the vibration and acoustic behavior of structures in thermal environments has been attracted increasingly interest recently. Matsunaga^[10] developed a two-dimensional global higher-order deformation theory utilizing the power series expansion method to study the natural frequency and critical temperature in thermal environments. Jeyaraj et al.^[11-13] conducted numerical simulation studies on sound vibration response of an isotropic plate, a composite plate and a sandwich plate in thermal environment by combing finite element method and boundary element method. It was found that the displacement response increases with the rise of temperature for isotropic plates. While, the vibration response decreases with the rise of temperature for the composite and sandwich panels. Geng and Li^[14] presented an analytical method to study the vibration and acoustic radiation characters of an isotropic plate in thermal environments. Similar conclusions were drawn as Jeyaraj^[11]. Later, Geng et al.^[15-16] studied the vibration and acoustic response of a clamped rectangular plate in thermal environments experimentally, numerically and theoretically. Based on equivalent non-classical theory, Liu^[17] studied the vibration and acoustic response of a rectangular sandwich plate that was applied to a concentrated harmonic force in thermal environments. Li^[18] also investigated the above problem on the theory of simplified piecewise low order shear deformation. The accuracy of the theoretical method was confirmed by FEM/BEM simulations. Li^[19] applied the similar method by using the first-order shear deformation plate theory to investigate the vibration and acoustic characteristics of asymmetric laminated plate in thermal environments.

Though lots of studies focus on the vibration behavior of sandwich panels with flexible core, and the dynamic and acoustic response of sandwich panel in thermal environments, respectively. However, few researches have been conducted on the vibration and acoustic characteristics of sandwich panels with both symmetric and anti-symmetric motions considered in thermal environments. Symmetric motions may have significant effects on the vibration and acoustic responses for sandwich panels with flexible core.

In this study, the analytical vibration response of the sandwich panels in thermal environments is solved with both symmetric and anti-symmetric motions taken into consideration. Then, the sound radiation is obtained by applying the Rayleigh integral. Validation and numerical studies are deeply discussed. In the end, there are the summary and conclusions.

2 Theoretical FormulationConsider a symmetric sandwich panel with dimension a×b, and set the x-direction along the a side of the panel. The face sheet and the core thickness are d_f and c, respectively, as shown in Fig. 1. The material properties of the face sheet are elasticity modulus E_f11, E_f22, Poisson's ratio μ_f12, shear modulus G_f12, mass density ρ_f, and thermal expansion coefficients α_f11, α_f22, respectively. The material properties of the core include elastic modulus, Poisson's ratio, shear modulus, thermal expansion coefficient and mass density which are denoted as E_c11, E_c22, E_c33, μ_c12, μ_c23, μ_c31, G_c12, G_c23, G_c31, ρ_c, α_c11, α_c22, respectively.

Figure 1
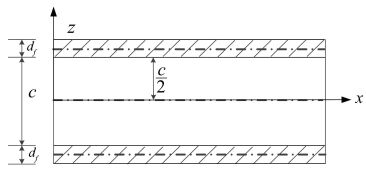Figure 1 The symmetric sandwich panel



2.1 Governing EquationsThe following assumptions are made for sandwich panels: a) The face sheets are modeled as elementary plates in bending and stretching. b) The transverse shear deformation is neglected in the thin face sheets and included in the thick core. c) The strain in the thickness direction of the core ε_cz≠0, that is, both anti-symmetric and symmetric deformation are considered. The displacement functions which are expanded from the one-dimension model given by Zhou and Crocker^[20] are assumed as follows:

$\begin{array}{l}{u_{\rm{t}}} = {u_{\rm{s}}} + {u_{\rm{a}}} - \left( {z - \frac{c}{2}} \right)\frac{{\partial {w_{\rm{t}}}}}{{\partial x}},{v_{\rm{t}}} = {v_{\rm{s}}} + {v_{\rm{a}}} - \left( {z - } \right.\\\;\;\;\;\;\;\left. {\frac{c}{2}} \right)\frac{{\partial {w_{\rm{t}}}}}{{\partial y}},{w_{\rm{t}}} = {w_{\rm{a}}} + {w_{\rm{s}}}\end{array}$

$\begin{array}{l}{u_{\rm{b}}} = {u_{\rm{s}}} + {u_{\rm{a}}} - \left( {z + \frac{c}{2}} \right)\frac{{\partial {w_{\rm{b}}}}}{{\partial x}},{v_{\rm{b}}} = {v_{\rm{s}}} - {v_{\rm{a}}} - \left( {z + } \right.\\\;\;\;\;\;\;\left. {\frac{c}{2}} \right)\frac{{\partial {w_{\rm{b}}}}}{{\partial y}},{w_{\rm{b}}} = {w_{\rm{a}}} - {w_{\rm{s}}}\end{array}$

$\begin{array}{l}{u_{\rm{c}}} = {u_{\rm{s}}} + \frac{2}{c}z{u_{\rm{a}}} + {\xi _1}\cos \left( {\frac{{{\rm{\pi }}z}}{c}} \right),{v_{\rm{c}}} = {v_{\rm{s}}} + \frac{2}{c}z{v_{\rm{a}}} + \\\;\;\;\;\;\;{\xi _2}\cos \left( {\frac{{{\rm{\pi }}z}}{c}} \right),{w_{\rm{c}}} = {w_{\rm{a}}} + \frac{2}{c}z{w_{\rm{s}}}\end{array}$

where, u, v and w are the in-plane and transverse displacements, and the subscripts t, b and c represent the top, bottom face sheet and the core, respectively. The subscripts a and s denote the displacements caused by anti-symmetric and symmetric motions, respectively, as shown in Fig. 2. The variables ξ₁, ξ₂ are used to describe the dilatational term of the core in the in-plane directions.

Figure 2
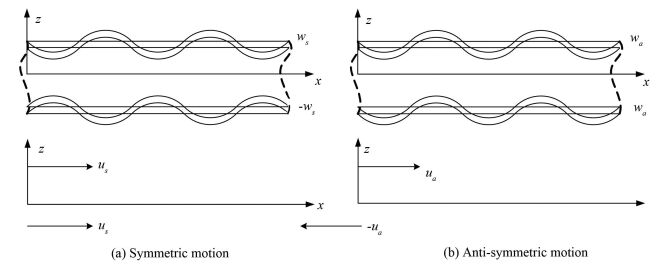Figure 2 Symmetric and anti-symmetric motions of sandwich panels



The thermo-elastic constitutive relations for elastic and orthotropic material can be expressed as:

$\left[ {\begin{array}{*{20}{c}}{{\sigma _{xx}}}\\{{\sigma _{yy}}}\\{{\sigma _{zz}}}\\{{\tau _{yz}}}\\{{\tau _{xz}}}\\{{\tau _{xy}}}\end{array}} \right] = \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}}{\varepsilon _{xx}^E}\\{\varepsilon _{yy}^E}\\{\varepsilon _{zz}^E}\\{\gamma _{yz}^E}\\{\gamma _{xz}^E}\\{\gamma _{xy}^E}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0&0\\{{C_{12}}}&{{C_{22}}}&{{C_{23}}}&0&0&0\\{{C_{13}}}&{{C_{23}}}&{{C_{33}}}&0&0&0\\0&0&0&{{C_{44}}}&0&0\\0&0&0&0&{{C_{55}}}&0\\0&0&0&0&0&{{C_{66}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{\varepsilon _{xx}} - \varepsilon _{xx}^T}\\{{\varepsilon _{yy}} - \varepsilon _{yy}^T}\\{{\varepsilon _{zz}} - \varepsilon _{zz}^T}\\{{\gamma _{yz}}}\\{{\gamma _{xz}}}\\{{\gamma _{xy}}}\end{array}} \right]$

where, ε_ij^E, ε_ij, ε_ij^T represent the elastic strains, real strains and thermal strains, respectively. C_ij are elements of the stiffness matrix of the material. The thermal strains can be written as follows:

$\begin{array}{l}\varepsilon _{xx}^T = {\alpha _{xx}}\Delta T\\\varepsilon _{yy}^T = {\alpha _{yy}}\Delta T\\\varepsilon _{zz}^T = {\alpha _{zz}}\Delta T\end{array}$

where, α_ij are coefficients of thermal expansion and ΔT is the temperature variation. The temperature is supposed uniform, we assume that the initial temperature of the panel is T₀=0 ℃ and the final steady temperature is T.

The strain energy expression of the face sheets and the core of sandwich panels can be written as:

$\begin{array}{l}{U_{t\left( b \right)}} = \frac{1}{2}\int_{{V_{t\left( b \right)}}} {\left[ {{\sigma _{xt\left( b \right)}}{{\left( {{\varepsilon _x} - \varepsilon _x^T} \right)}_{t\left( b \right)}} + {\sigma _{yt\left( b \right)}}} \right.} \\\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {{\varepsilon _y} - \varepsilon _y^T} \right)}_{t\left( b \right)}} + {\tau _{xyt\left( b \right)}}{\gamma _{xyt\left( b \right)}}} \right]{\rm{d}}{V_{t\left( b \right)}}\end{array}$

$\begin{array}{l}{U_c} = \frac{1}{2}\int_{{V_c}} {\left[ {{\sigma _{xc}}\left( {{\varepsilon _{xc}} - \varepsilon _{xc}^T} \right) + {\sigma _{yc}}\left( {{\varepsilon _{yc}} - \varepsilon _{yc}^T} \right) + } \right.} \\\;\;\;\;\;\;\;\;{\sigma _{zc}}\left( {{\varepsilon _{zc}} - \varepsilon _{zc}^T} \right) + {\tau _{yzc}}{\gamma _{yzc}} + {\tau _{xzc}}{\gamma _{xzc}} + \\\;\;\;\;\;\;\;\;\left. {{\tau _{xyc}}{\gamma _{xyc}}} \right]{\rm{d}}{V_c}\end{array}$

The total kinetic energy of the face sheets and core can be expressed as:

$\begin{array}{l}{T_{t\left( b \right)}} = \frac{1}{2}\int_{{V_{t\left( b \right)}}} {{\rho _f}\left( {{{\left( {\frac{{\partial {u_{t\left( b \right)}}}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial {v_{t\left( b \right)}}}}{{\partial t}}} \right)}^2} + } \right.} \\\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{\partial {w_{t\left( b \right)}}}}{{\partial t}}} \right)}^2}} \right){\rm{d}}{V_{t\left( b \right)}}\end{array}$

$\begin{array}{l}{T_c} = \frac{1}{2}\int_{{V_c}} {{\rho _c}\left( {{{\left( {\frac{{\partial {u_c}}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial {v_c}}}{{\partial t}}} \right)}^2} + } \right.} \\\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{\partial {w_c}}}{{\partial t}}} \right)}^2}} \right){\rm{d}}{V_c}\end{array}$

For symmetric sandwich panels, the initial stresses are the thermal stresses caused by the uniform thermal environment which can be obtained by the thermo-elastic constitutive relations. Assuming that the initial stress in the thickness direction is zero. Then strain energy caused by the initial stresses can be expressed as^[10]:

$\begin{array}{l}{U^T} = \frac{1}{2}\int_V {\left[ {\sigma _x^T\left( {{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2}} \right)} \right. + } \\\;\;\;\;\;\;\;\;\;\left. {\sigma _y^T\left( {{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial y}}} \right)}^2}} \right)} \right]{\rm{d}}V\end{array}$

Assuming that the external load q(x, y, t) is imposed on the top face sheet. The work of the external load can be written as:

${W_e} = \int_0^a {\int_0^b {q{w_t}{\rm{d}}x{\rm{d}}y} } = \int_0^a {\int_0^b {q\left( {{w_a} + {w_s}} \right){\rm{d}}x{\rm{d}}y} } $

Substituting the strain energy, the kinetic energy and the external load work into the following Hamilton's principle

$\delta \int_{{t_1}}^{{t_2}} {\left( {T - U - {U^T}} \right){\rm{d}}t} + \delta \int_{{t_1}}^{{t_2}} {{W_e}{\rm{d}}t} = 0$

Through the variational calculation, the following governing equations can be derived for the symmetric orthotropic sandwich panels in thermal environments.

$\begin{array}{l}\left( {D_{11}^{f2} + N_{xf}^{T2}} \right)\frac{{{\partial ^3}{u_s}}}{{\partial {x^3}}} + \left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{yf}^{T2}} \right)\frac{{{\partial ^3}{u_s}}}{{\partial x\partial {y^2}}} + \\\left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{yf}^{T2}} \right)\frac{{{\partial ^3}{v_s}}}{{\partial {x^2}\partial y}} + \left( {D_{22}^{f2} + N_{yf}^{T2}} \right) \cdot \\\frac{{{\partial ^3}{v_s}}}{{\partial {y^3}}} - \left( {D_{11}^{f3} + N_{xf}^{T3}} \right)\frac{{{\partial ^4}{w_s}}}{{\partial {x^4}}} - \left( {2D_{12}^{f3} + 4D_{66}^{f3} + } \right.\\\left. {N_{xf}^{T3} + N_{yf}^{T3}} \right)\frac{{{\partial ^4}{w_s}}}{{\partial {x^2}\partial {y^2}}} - \left( {D_{22}^{f3} + N_{yf}^{T3}} \right)\frac{{{\partial ^4}{w_s}}}{{\partial {y^4}}} + \\\left( {N_{xf}^{T1} + \frac{{N_{xc}^{T1}}}{3}} \right)\frac{{{\partial ^2}{w_s}}}{{\partial {x^2}}} + \left( {N_{yf}^{T1} + \frac{{N_{yc}^{T1}}}{3}} \right)\frac{{{\partial ^2}{w_s}}}{{\partial {y^2}}} - \\2\left( {{C_{13c}}\frac{{\partial {u_s}}}{{\partial x}} + {C_{23c}}\frac{{\partial {v_s}}}{{\partial y}}} \right) - \frac{4}{{\rm{\pi }}}\left( {\left( {{C_{13c}} + {C_{55c}}} \right) \cdot } \right.\\\left. {\frac{{\partial {\xi _1}}}{{\partial x}} + \left( {{C_{23c}} + {C_{44c}}} \right)\frac{{\partial {\xi _2}}}{{\partial y}}} \right) - \frac{4}{c}{C_{33c}}{w_s} + \\\frac{1}{3}\left( {D_{55}^{c1}\frac{{{\partial ^2}{w_s}}}{{\partial {x^2}}} + D_{44}^{c1}\frac{{{\partial ^2}{w_s}}}{{\partial {y^2}}}} \right) - {I^{f2}}\left( {\frac{{{\partial ^3}{u_s}}}{{\partial x\partial {t^2}}} + } \right.\\\left. {\frac{{{\partial ^3}{v_s}}}{{\partial y\partial {t^2}}}} \right) + {I^{f3}}\left( {\frac{{{\partial ^4}{w_s}}}{{\partial {x^2}\partial {t^2}}} + \frac{{{\partial ^4}{w_s}}}{{\partial {y^2}\partial {t^2}}}} \right) - \left( {{I^{f1}} + \frac{{{I^{c1}}}}{3}} \right) \cdot \\\frac{{{\partial ^2}{w_s}}}{{\partial {t^2}}} + q = 0\end{array}$ (1)

$\begin{array}{l}\left( {\left( {D_{11}^{f1} + N_{xf}^{T1}} \right) + \left( {D_{11}^{c1} + N_{xc}^{T1}} \right)} \right)\frac{{{\partial ^2}{u_s}}}{{\partial {x^2}}} + \left( {\left( {D_{66}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {N_{yf}^{T1}} \right) + \left( {D_{66}^{c1} + N_{yc}^{T1}} \right)} \right)\frac{{{\partial ^2}{u_s}}}{{\partial {y^2}}} - \left( {D_{11}^{f2} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {N_{xf}^{T2}} \right)\frac{{{\partial ^3}{w_s}}}{{\partial {x^3}}} + \left( {\left( {D_{12}^{f1} + D_{66}^{f1}} \right) + \left( {D_{12}^{c1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {D_{66}^{c1}} \right)} \right)\frac{{{\partial ^2}{v_s}}}{{\partial x\partial y}} - \left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{yf}^{T2}} \right)\frac{{{\partial ^3}{w_s}}}{{\partial x\partial {y^2}}} + \\\;\;\;\;\;\;\;\;\;\;\;\;2{C_{13c}}\frac{{\partial {w_s}}}{{\partial x}} + {I^{f2}}\frac{{{\partial ^3}{w_s}}}{{\partial x\partial {t^2}}} + \frac{2}{{\rm{\pi }}}\left( {\left( {D_{11}^{c1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {N_{xc}^{T1}} \right)\frac{{{\partial ^2}{\xi _1}}}{{\partial {x^2}}} + \left( {D_{66}^{c1} + N_{yc}^{T1}} \right)\frac{{{\partial ^2}{\xi _1}}}{{\partial {y^2}}} + \left( {D_{12}^{c1} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {D_{66}^{c1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial x\partial y}}} \right) - \left( {{I^{f1}} + {I^{c1}}} \right)\frac{{{\partial ^2}{u_s}}}{{\partial {t^2}}} - \frac{2}{{\rm{\pi }}}{I^{c1}}\\\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}{\xi _1}}}{{\partial {t^2}}} = 0\end{array}$ (2)

$\begin{array}{l}\left( {\left( {D_{12}^{f1} + D_{66}^{f1}} \right) + \left( {D_{12}^{c1} + D_{66}^{c1}} \right)} \right)\frac{{{\partial ^2}{u_s}}}{{\partial x\partial y}} + \left( {\left( {D_{66}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {N_{xf}^{T1}} \right) + \left( {D_{66}^{c1} + N_{xc}^{T1}} \right)} \right)\frac{{{\partial ^2}{v_s}}}{{\partial {x^2}}} - \left( {D_{22}^{f2} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {N_{yf}^{T2}} \right)\frac{{{\partial ^3}{w_s}}}{{\partial {y^3}}} + \left( {\left( {D_{22}^{f1} + D_{yf}^{T1}} \right) + \left( {D_{22}^{c1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {N_{yc}^{T1}} \right)} \right)\frac{{{\partial ^2}{v_s}}}{{\partial {y^2}}} - \left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{xf}^{T2}} \right)\frac{{{\partial ^3}{w_s}}}{{\partial {x^2}\partial y}} + \\\;\;\;\;\;\;\;\;\;\;\;\;2{C_{23c}}\frac{{\partial {w_s}}}{{\partial y}} + {I^{f2}}\frac{{{\partial ^3}{w_s}}}{{\partial y\partial {t^2}}} + \frac{2}{{\rm{\pi }}}\left( {\left( {D_{12}^{c1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {D_{66}^{c1}} \right)\frac{{{\partial ^2}{\xi _1}}}{{\partial x\partial y}} + \left( {D_{66}^{c1} + N_{xc}^{T1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial {x^2}}} + \left( {D_{22}^{c1} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {N_{yc}^{T1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial {y^2}}}} \right) - \left( {{I^{f1}} + {I^{c1}}} \right)\frac{{{\partial ^2}{v_s}}}{{\partial {t^2}}} - \frac{2}{{\rm{\pi }}}{I^{c1}} \cdot \\\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}{\xi _2}}}{{\partial {t^2}}} = 0\end{array}$ (3)

$\begin{array}{l}\frac{2}{{\rm{\pi }}}\left( {\left( {D_{11}^{c1} + N_{xc}^{T1}} \right)\frac{{{\partial ^2}{u_s}}}{{\partial {x^2}}} + \left( {D_{66}^{c1} + N_{yc}^{T1}} \right)\frac{{{\partial ^2}{u_s}}}{{\partial {y^2}}} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {D_{12}^{c1} + D_{66}^{c1}} \right)\frac{{{\partial ^2}{v_s}}}{{\partial x\partial y}}} \right) + \frac{4}{{\rm{\pi }}}\left( {{{\bar C}_{13c}} + {{\bar C}_{55c}}} \right) \cdot \\\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial {w_s}}}{{\partial x}} - \frac{{{\pi ^2}}}{{2c}}{C_{55c}}{\xi _1} + \frac{1}{2}\left( {\left( {D_{11}^{c1} + N_{xc}^{T1}} \right) \cdot } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}{\xi _1}}}{{\partial {x^2}}} + \left( {D_{66}^{c1} + N_{yc}^{T1}} \right)\frac{{{\partial ^2}{\xi _1}}}{{\partial {y^2}}} + \left( {D_{12}^{c1} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {D_{66}^{c1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial x\partial y}}} \right) - \frac{2}{{\rm{\pi }}}{I^{c1}}\frac{{{\partial ^2}{u_s}}}{{\partial {t^2}}} - \frac{{{I^{c1}}}}{2}\frac{{{\partial ^2}{\xi _1}}}{{\partial {t^2}}} = 0\end{array}$ (4)

$\begin{array}{l}\frac{2}{{\rm{\pi }}}\left( {\left( {D_{12}^{c1} + D_{66}^{c1}} \right)\frac{{{\partial ^2}{u_s}}}{{\partial x\partial y}} + \left( {D_{66}^{c1} + N_{xc}^{T1}} \right)\frac{{{\partial ^2}{v_s}}}{{\partial {x^2}}} + \left( {D_{22}^{c1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {N_{yc}^{T1}} \right)\frac{{{\partial ^2}{v_s}}}{{\partial {y^2}}}} \right) + \frac{4}{{\rm{\pi }}}\left( {{{\bar C}_{23c}} + {{\bar C}_{44c}}} \right)\frac{{\partial {w_s}}}{{\partial y}} - \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\pi ^2}}}{{2c}}{C_{44c}}{\xi _2} + \frac{1}{2}\left( {\left( {D_{12}^{c1} + D_{66}^{c1}} \right)\frac{{{\partial ^2}{\xi _1}}}{{\partial x\partial y}} + } \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {D_{66}^{c1} + N_{xc}^{T1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial {x^2}}} + \left( {D_{22}^{c1} + N_{yc}^{T1}} \right)\frac{{{\partial ^2}{\xi _2}}}{{\partial {y^2}}}} \right) - \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{2}{{\rm{\pi }}}{I^{c1}}\frac{{{\partial ^2}{v_s}}}{{\partial {t^2}}} - \frac{{{I^{c1}}}}{2}\frac{{{\partial ^2}{\xi _2}}}{{\partial {t^2}}} = 0\end{array}$ (5)

$\begin{array}{l}\left( {D_{11}^{f2} + N_{xf}^{T2}} \right)\frac{{{\partial ^3}{u_a}}}{{\partial {x^3}}} + \left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{yf}^{T2}} \right)\frac{{{\partial ^3}{u_a}}}{{\partial x\partial {y^2}}} + \\\;\;\;\;\;\;\;\;\;\left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{xf}^{T2}} \right)\frac{{{\partial ^3}{v_a}}}{{\partial {x^2}\partial y}} + \left( {D_{22}^{f2} + N_{yf}^{T2}} \right) \cdot \\\;\;\;\;\;\;\;\;\;\frac{{{\partial ^3}{v_a}}}{{\partial {y^3}}} - \left( {D_{11}^{f3} + N_{xf}^{T3}} \right)\frac{{{\partial ^4}{w_a}}}{{\partial {x^4}}} - \left( {2D_{12}^{f3} + 4D_{66}^{f3} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {N_{xf}^{T3} + N_{yf}^{T3}} \right)\frac{{{\partial ^4}{w_a}}}{{\partial {x^2}\partial {y^2}}} - \left( {D_{22}^{f3} + N_{yf}^{T3}} \right)\frac{{{\partial ^4}{w_a}}}{{\partial {y^4}}} + \\\;\;\;\;\;\;\;\;\;\left( {N_{xf}^{T1} + N_{xc}^{T1}} \right)\frac{{{\partial ^2}{w_a}}}{{\partial {x^2}}} + \left( {N_{yf}^{T1} + N_{yc}^{T1}} \right)\frac{{{\partial ^2}{w_a}}}{{\partial {y^2}}} + \\\;\;\;\;\;\;\;\;\;2\left( {{C_{55c}}\frac{{\partial {u_a}}}{{\partial x}} + {{\bar C}_{44c}}\frac{{\partial {v_a}}}{{\partial y}}} \right) + \left( {D_{55}^{c1}\frac{{{\partial ^2}{w_a}}}{{\partial {x^2}}} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {D_{44}^{c1}\frac{{{\partial ^2}{w_a}}}{{\partial {y^2}}}} \right) - {I^{f2}}\left( {\frac{{{\partial ^3}{u_a}}}{{\partial x\partial {t^2}}} + \frac{{{\partial ^3}{v_a}}}{{\partial y\partial {t^2}}}} \right) + {I^{f3}}\left( {\frac{{{\partial ^4}{w_a}}}{{\partial {x^2}\partial {t^2}}} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {\frac{{{\partial ^4}{w_a}}}{{\partial {y^2}\partial {t^2}}}} \right) - \left( {{I^{f1}} + {I^{c1}}} \right)\frac{{{\partial ^2}{w_a}}}{{\partial {t^2}}} + q = 0\end{array}$ (6)

$\begin{array}{l}\left( {\left( {D_{11}^{f1} + N_{xf}^{T1}} \right) + \frac{1}{3}\left( {D_{11}^{c1} + N_{xc}^{T1}} \right)} \right)\frac{{{\partial ^2}{u_a}}}{{\partial {x^2}}} + \left( {\left( {D_{66}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {N_{yf}^{T1}} \right) + \frac{1}{3}\left( {D_{66}^{c1} + N_{yc}^{T1}} \right)} \right)\frac{{{\partial ^2}{u_a}}}{{\partial {y^2}}} + \left( {\left( {D_{12}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {D_{66}^{f1}} \right) + \frac{1}{3}\left( {D_{12}^{c1} + D_{66}^{c1}} \right)} \right)\frac{{{\partial ^2}{v_a}}}{{\partial x\partial y}} - \left( {D_{11}^{f2} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {N_{xf}^{T2}} \right)\frac{{{\partial ^3}{w_a}}}{{\partial {x^3}}} - \frac{4}{c}{C_{55c}}{u_a} - \left( {D_{12}^{f2} + 2D_{66}^{f2} + N_{yf}^{T2}} \right)\\\;\;\;\;\;\;\;\;\;\frac{{{\partial ^3}{w_a}}}{{\partial x\partial {y^2}}} - 2{C_{55c}}\frac{{\partial {w_a}}}{{\partial x}} - \left( {{I^{f1}} + \frac{{{I^{c1}}}}{3}} \right)\frac{{{\partial ^2}{u_a}}}{{\partial {t^2}}} + \\\;\;\;\;\;\;\;\;\;{I^{f2}}\frac{{{\partial ^3}{w_a}}}{{\partial x\partial {t^2}}} = 0\end{array}$ (7)

$\begin{array}{l}\left( {\left( {D_{66}^{f1} + N_{66}^{f1}} \right) + \frac{1}{3}\left( {D_{12}^{c1} + N_{66}^{c1}} \right)} \right)\frac{{{\partial ^2}{u_a}}}{{\partial x\partial y}} + \left( {\left( {D_{66}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {N_{xf}^{T1}} \right) + \frac{1}{3}\left( {D_{66}^{c1} + N_{xc}^{T1}} \right)} \right)\frac{{{\partial ^2}{v_a}}}{{\partial {x^2}}} + \left( {\left( {D_{22}^{f1} + } \right.} \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {D_{yf}^{T1}} \right) + \frac{1}{3}\left( {D_{22}^{c1} + N_{yc}^{T1}} \right)} \right)\frac{{{\partial ^2}{v_a}}}{{\partial {y^2}}} - \left( {D_{12}^{f2} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {2D_{66}^{f2} + N_{xf}^{T2}} \right)\frac{{{\partial ^3}{w_a}}}{{\partial {x^2}\partial y}} - \left( {D_{22}^{f2} + N_{yf}^{T2}} \right) \cdot \frac{{{\partial ^3}{w_a}}}{{\partial {y^3}}} - \\\;\;\;\;\;\;\;\;\;\frac{4}{c}{C_{44c}}{v_a} - 2{C_{44c}}\frac{{\partial {w_a}}}{{\partial y}} - \left( {{I^{f1}} + \frac{{{I^{c1}}}}{3}} \right)\frac{{{\partial ^2}{v_a}}}{{\partial {t^2}}} + \\\;\;\;\;\;\;\;\;\;{I^{f2}}\frac{{{\partial ^3}{w_a}}}{{\partial x\partial {t^2}}} = 0\end{array}$ (8)

where:

$\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{D_{ij}^{fk}}&{{I^{fk}}}&{N_{xf}^{Tk}}&{N_{yf}^{Tk}}\end{array}} \right] = \\\;\;\;\;\;\;\;\;2\left[ {\begin{array}{*{20}{c}}{{C_{ijf}}}&{{\rho _f}}&{\sigma _{xf}^T}&{\sigma _{yf}^T}\end{array}} \right]d_f^k/k,\;\;\;\;\;\;\left( {k = 1,2,3} \right)\end{array}$

$\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{D_{ij}^{c1}}&{{I^{c1}}}&{N_{xc}^{T1}}&{N_{yc}^{T1}}\end{array}} \right] = \\\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{{C_{ijc}}}&{{\rho _c}}&{\sigma _{xc}^T}&{\sigma _{yc}^T}\end{array}} \right]c\end{array}$

It can be observed from the above governing equations that symmetric (Eqs. (1)-(5)) and anti-symmetric (Eqs. (6)-(8)) motions are uncoupled for the symmetric sandwich panels.

2.2 Free Vibration AnalysisFor free vibration (q=0), the displacements of a simply supported sandwich panel can be written in the form of double trigonometric series as follows ^[21]:

$\left\{ \begin{array}{l}{w_s} = \sum\limits_{m,n} {{{\bar W}_{smn}}\sin \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{w_a} = \sum\limits_{m,n} {{{\bar W}_{amn}}\sin \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{u_s} = \sum\limits_{m,n} {{{\bar U}_{smn}}\cos \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{u_a} = \sum\limits_{m,n} {{{\bar U}_{amn}}\cos \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{v_s} = \sum\limits_{m,n} {{{\bar V}_{smn}}\sin \left( {m{\rm{\pi }}x/a} \right)\cos \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{v_a} = \sum\limits_{m,n} {{{\bar V}_{amn}}\sin \left( {m{\rm{\pi }}x/a} \right)\cos \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{\xi _1} = \sum\limits_{m,n} {{{\bar X}_{1mn}}\cos \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \\{\xi _2} = \sum\limits_{m,n} {{{\bar X}_{2mn}}\sin \left( {m{\rm{\pi }}x/a} \right)\cos \left( {n{\rm{\pi }}y/b} \right){e^{{\rm{j}}{\omega _{mn}}t}}} \end{array} \right.$ (9)

Substituting Eq. (9) into Eqs. (1)-(8) yields:

$\left\{ \begin{array}{l}\left( {{\mathit{\boldsymbol{A}}_s} + \omega _{mn}^2{\mathit{\boldsymbol{B}}_s}} \right){\left[ {\begin{array}{*{20}{c}}{{{\bar W}_{smn}}}&{{{\bar U}_{smn}}}&{{{\bar V}_{smn}}}&{{{\bar X}_{1mn}}}&{{{\bar X}_{2mn}}}\end{array}} \right]^{\rm{T}}} = 0\\\left( {{\mathit{\boldsymbol{A}}_{\rm{a}}} + \omega _{mn}^2{\mathit{\boldsymbol{B}}_a}} \right){\left[ {\begin{array}{*{20}{c}}{{{\bar W}_{amn}}}&{{{\bar U}_{amn}}}&{{{\bar V}_{amn}}}\end{array}} \right]^{\rm{T}}} = 0\end{array} \right.$ (10)

The natural frequency can be solved by setting det (A_s+ω_mn²B_s)=0 for symmetric motion and det (A_a+ω_mn²B_a)=0 for anti-symmetric motion. There are five solutions for the modes of vibration which are symmetric about the plane z=0. The most important solution is the dilatational mode. Of the other solutions, two represent the longitudinal modes in the face sheets and the rest two describe the wave motion in the core. For anti-symmetric motion, there are three solutions. One describes the flexural mode and the other two represent longitudinal vibrations in the plane of the panel. In addition, the critical temperature can be derived by setting det (A_s(a)+ω_s(a)mn²B_s(a))=0 with ω_s(a)11=0.

Substituting the natural frequency ω_mn into Eq. (10) and assuming that W_amn=W_smn=1, U_smn, V_smn, X_1mn, X_2mn, U_amn, V_amn can be obtained. Consequently, the mode functions are determined.

2.3 Dynamic AnalysisThe forced vibration analysis of the sandwich panel which is subjected to a concentrated harmonic force is analyzed in this section. The dynamic response can be expanded in terms of mode functions based on the mode superposition principle as follows:

$\left\{ \begin{array}{l}{w_s} = \sum\limits_{m,n} {{W_{smn}}\left( {x,y} \right){T_{smn}}\left( t \right)} \\{u_s} = \sum\limits_{m,n} {{U_{smn}}\left( {x,y} \right){T_{smn}}\left( t \right)} \\{v_s} = \sum\limits_{m,n} {{V_{smn}}\left( {x,y} \right){T_{smn}}\left( t \right)} \\{\xi _1} = \sum\limits_{m,n} {{X_{1mn}}\left( {x,y} \right){T_{smn}}\left( t \right)} \\{\xi _2} = \sum\limits_{m,n} {{X_{2mn}}\left( {x,y} \right){T_{smn}}\left( t \right)} \\{w_a} = \sum\limits_{m,n} {{W_{amn}}\left( {x,y} \right){T_{amn}}\left( t \right)} \\{u_a} = \sum\limits_{m,n} {{U_{amn}}\left( {x,y} \right){T_{amn}}\left( t \right)} \\{v_a} = \sum\limits_{m,n} {{V_{amn}}\left( {x,y} \right){T_{amn}}\left( t \right)} \end{array} \right.$ (11)

Substituting Eq. (11) into the governing equations and combine Eq. (10), for symmetric motion the following equations are obtained.

$\begin{array}{l}\sum\limits_{m,n} {\left( {\left( {{I^{f3}}\left( {{{\left( {\frac{{m\pi }}{a}} \right)}^2} + {{\left( {\frac{{n\pi }}{b}} \right)}^2}} \right) + \left( {{I^{f1}} + \frac{{{I^{c1}}}}{3}} \right)} \right){{\bar W}_{smn}} - } \right.} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{I^{f2}}\left( {\frac{{m\pi }}{a}{{\bar U}_{smn}} + \frac{{n\pi }}{b}{{\bar V}_{smn}}} \right)} \right) \times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\sin \left( {\frac{{m\pi }}{a}x} \right)\sin \left( {\frac{{n\pi }}{b}y} \right)\left( {{{\ddot T}_{smn}} + \omega _{smn}^2{T_{smn}}} \right) = \\\;\;\;\;\;\;\;\;\;\;\;\;\;q\left( {x,y,t} \right)\end{array}$ (12)

$\begin{array}{l}\sum\limits_{m,n} {\left( {{I^{f2}}\frac{{m\pi }}{a} - \left( {{I^{f1}} + {I^{c1}}} \right){{\bar U}_{smn}} - \frac{2}{{\rm{\pi }}}{I^{c1}}{{\bar X}_{1mn}}} \right) \cdot } \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cos \left( {\frac{{m\pi }}{a}x} \right)\sin \left( {\frac{{n\pi }}{b}y} \right)\left( {{{\ddot T}_{smn}} + \omega _{smn}^2{T_{smn}}} \right) = 0\end{array}$ (13)

$\begin{array}{l}\sum\limits_{m,n} {\left. {\frac{{\left( {{I^{f2}}n{\rm{\pi }}} \right.}}{b} - \left( {{I^{f1}} + {I^{c1}}} \right){{\bar V}_{smn}} - \frac{2}{{\rm{\pi }}}{I^{c1}}{{\bar X}_{2mn}}} \right)} \cdot \\\;\;\;\;\;\sin \left( {\frac{{m{\rm{\pi }}}}{a}x} \right)\cos \left( {\frac{{n{\rm{\pi }}}}{b}y} \right)\left( {{{\ddot T}_{smn}} + \omega _{smn}^2{T_{smn}}} \right) = 0\end{array}$ (14)

$\begin{array}{l}\sum\limits_{m,n} {\left( {\frac{2}{{\rm{\pi }}}{I^{c1}}{{\bar U}_{smn}} + \frac{{{I^{c1}}}}{2}{{\bar X}_{1mn}}} \right)\cos \left( {\frac{{m{\rm{\pi }}}}{a}x} \right)\sin \left( {\frac{{n{\rm{\pi }}}}{b}y} \right) \cdot } \\\;\;\;\;\;\left( {{{\ddot T}_{smn}} + \omega _{smn}^2{T_{smn}}} \right) = 0\end{array}$ (15)

$\begin{array}{l}\sum\limits_{m,n} {\left( {\frac{2}{{\rm{\pi }}}{I^{c1}}{{\bar V}_{smn}} + \frac{{{I^{c1}}}}{2}{{\bar X}_{2mn}}} \right)\sin \left( {\frac{{m{\rm{\pi }}}}{a}x} \right)\cos \left( {\frac{{n{\rm{\pi }}}}{b}y} \right)\left( {{{\ddot T}_{smn}} + } \right.} \\\;\;\;\;\;\left. {\omega _{smn}^2{T_{smn}}} \right) = 0\end{array}$ (16)

Multiplying Eqs. (12)-(16) by W_sij, U_sij, V_sij, X_1ij, X_2ij, respectively, then adding them together and integrating over the entire surface. By utilizing the orthogonality of the mode shapes, the following equation can be obtained.

${{\ddot T}_{smn}} + \omega _{smn}^2{T_{smn}} = {Q_{smn}}/{M_{smn}}$ (17)

where:

${Q_{mn}} = \int_0^a {\int_0^b {q\left( {x,y,t} \right)\sin \left( {\frac{{m\pi }}{a}x} \right)\sin \left( {\frac{{n\pi }}{b}y} \right){\rm{d}}x{\rm{d}}y} } $

$\begin{array}{l}{M_{smn}} = \frac{{ab}}{4}\left( {\left( {{I^{f3}}\left( {{{\left( {\frac{{m{\rm{\pi }}}}{a}} \right)}^2} + {{\left( {\frac{{n{\rm{\pi }}}}{b}} \right)}^2}} \right) + \left( {{I^{f1}} + } \right.} \right.} \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {\frac{{{I^{c1}}}}{3}} \right)} \right) - \left( {{I^{f1}} + {I^{c1}}} \right)\left( {\bar U_{smn}^2 + \bar V_{smn}^2} \right) + \frac{{{I^{c1}}}}{2}\left( {\bar X_{1mn}^2 + } \right.\\\;\;\;\;\;\;\;\;\;\left. {\left. {\bar X_{2mn}^2} \right)} \right)\end{array}$

Considering a transverse concentrate harmonic force with frequency ω imposed on the top face sheet at point (x₀, y₀), which can be indicated by Dirac function as follows:

$q\left( {x,y,t} \right) = {q_0}\delta \left( {x - {x_0},y - {y_0}} \right){e^{{\rm{j}}\omega t}}$ (18)

In view of Eq. (18), Eq. (17) can be solved as:

${T_{smn}}\left( t \right) = \frac{{{q_0}\sin \left( {m{\rm{\pi }}{x_0}/a} \right)\sin \left( {n{\rm{\pi }}{y_0}/b} \right){e^{{\rm{j}}\omega t}}}}{{{M_{smn}}\left( {\omega _{smn}^2 - {\omega ^2}} \right)}}$

Then, the symmetric vibration of the sandwich panel under transverse concentrate harmonic force can be written as:

${w_s}\left( {x,y,t} \right) = \sum\limits_{m,n} {\sin \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){T_{smn}}\left( t \right)} $

Similar to the process of solving the symmetric vibration response, the following equations can be derived for anti-symmetric motion.

${{\ddot T}_{amn}} + \omega _{amn}^2{T_{amn}} = {Q_{amn}}/{M_{amn}}$

where:

$\begin{array}{l}{M_{amn}} = \frac{{ab}}{4}\left( {\left( {{I^{f3}}\left( {{{\left( {\frac{{m{\rm{\pi }}}}{a}} \right)}^2} + {{\left( {\frac{{n{\rm{\pi }}}}{b}} \right)}^2}} \right) + \left( {{I^{f1}} + {I^{c1}}} \right)} \right) - } \right.\\\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {{I^{f1}} + \frac{{{I^{c1}}}}{3}} \right)\left( {\bar U_{amn}^2 + \bar V_{amn}^2} \right)} \right)\end{array}$

Considering Eq. (18), we have

${T_{amn}}\left( t \right) = \frac{{{q_0}\sin \left( {m{\rm{\pi }}{x_0}/a} \right)\sin \left( {n{\rm{\pi }}{y_0}/b} \right){e^{{\rm{j}}\omega t}}}}{{{M_{amn}}\left( {\omega _{amn}^2 - {\omega ^2}} \right)}}$

So the anti-symmetric vibration of the sandwich panel under transverse concentrate harmonic force can be expressed as:

${w_a}\left( {x,y,t} \right) = \sum\limits_{m,n} {\sin \left( {m{\rm{\pi }}x/a} \right)\sin \left( {n{\rm{\pi }}y/b} \right){T_{amn}}\left( t \right)} $

Therefore, the transverse displacement and velocity response of the top face sheet can be obtained as:

$\begin{array}{*{20}{c}}{{w_t}\left( {x,y,t} \right) = {w_a}\left( {x,y,t} \right) + {w_s}\left( {x,y,t} \right)}\\{{v_t}\left( {x,y,t} \right) = j\omega {w_t}\left( {x,y,t} \right)}\end{array}$

Similarly, the structural responses of the bottom face sheet can be derived.

The sound pressure radiated from the plate at the observation point (x_p, y_p, z_p) can be acquired by applying the Rayleigh's integral as:

$p\left( {{x_p},{y_p},{z_p},\omega } \right) = \frac{{j\omega {\rho _0}}}{{2{\rm{\pi }}}}\int_s {\frac{{v\left( {x,y} \right){e^{ - {\rm{j}}kR}}}}{R}{\rm{d}}s} $

where, ρ₀ is the density of the fluid; R=$\sqrt {{{\left( {{x_p} - x} \right)}^2} + {{\left( {{y_p} - y} \right)}^2} + {{\left( {{z_p} - z} \right)}^2}}$ is the distance between the vibrating point on the plate and the observation point in the acoustic field; k is the wave number, which is evaluated by ω/c₀, and c₀ is the speed of sound in the fluid medium; ds is the infinitesimal of the vibrating surface.

3 Model ValidationIn order to validate the proposed model, two sandwich panels A and B having all edges simply supported analyzed by Frostig^[8] and Rabinovitch^[9] and Li^[18] are considered. Panel A is consist of two glass fiber face sheets with material properties E_f=18 GPa, G_f=6.92 GPa, μ_f=0.3, ρ_f=2 000 kg/m³ and a Divinycell foam core with the equivalent material properties E_c=85 MPa, G_c=16 MPa, ρ_c=100 kg/m³. The dimension of panel A is 1.2 m×1.2 m, the face sheet and core thickness are 6 mm and 60 mm, respectively. The dimension of panel B is 400 mm×300 mm, with the face sheet thickness 0.5 mm and the core thickness 9 mm. The face sheet material properties are E_f1=132 GPa, E_f2=10.3 GPa, G_f12=6.5 GPa, μ_f12=0.25, ρ_f=1 570 kg/m³, α_f1=1.2×10^-6/℃, α_f2=2.4×10^-5/℃. The material properties of the core are E_c=10 MPa, μ_c=0.3, ρ_c=40 kg/m³, α_c=1.8×10^-7/℃. In addition, structural damping ratio is assumed to be 0.001 for panel B.

3.1 Validation for Natural FrequenciesThe proposed model is verified by comparing the natural frequencies of panel A obtained from the present model and those obtained from models developed by Frostig^[8] and Rabinovitch^[9] without considering the thermal effect. Since there are no results available in literatures for symmetric motion natural frequencies of sandwich panels in thermal environments, only anti-symmetric motion natural frequencies of panel B are compared with Li^[18] and MSC.Nastran results.

The natural frequencies obtained by the present analysis as well as those reported in Frostig^[8] and Rabinovitch^[9] are listed in Table 1 for the wave number m=1, n=1. The corresponding mode shapes given by Rabinovitch^[9] and the present model are shown in Fig. 3 and Fig. 4, respectively. The six modes are corresponding to the flexural, symmetric and anti-symmetric motions in x direction, symmetric and anti-symmetric motions in y direction and dilatational mode, respectively. Among the six modes, the flexural and dilatational modes are of paramount importance.

表 1
Table 1 Comparison of natural frequencies between present analysis and other models in literatures (Hz)

Mode No.Model Ⅰ (Frostig)^[8]Model Ⅱ (Frostig)^[8]Ref.[9](Elmalich)Present results

1101.4691.90101.46101.17

2983.97976.52980.87988.51

31470.901469.021466.171469.30

41663.221622.741657.781635.50

52059.202053.952052.732056.40

62357.652339.052349.772374.30



Table 1 Comparison of natural frequencies between present analysis and other models in literatures



It is observed from Table 1, Fig. 3 and Fig. 4 that the natural frequencies and mode shapes for the wave number m=1, n=1 obtained from the present analysis are in good agreement with those in literatures.

Figure 3
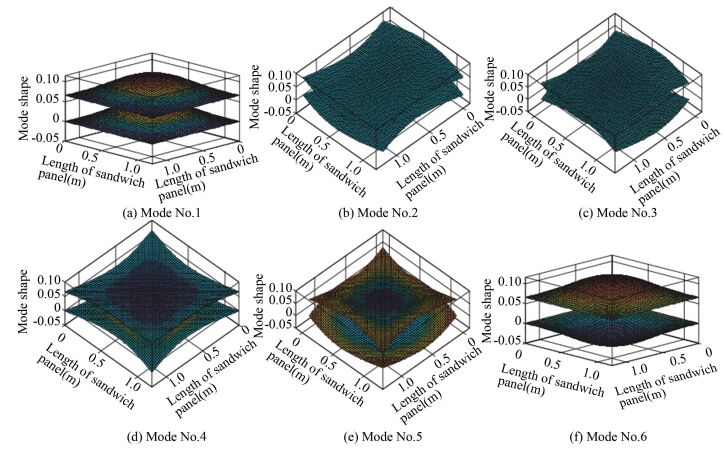Figure 3 Mode shape associated with wave number m=1, n=1 derived by Rabinovitch^[9]



Figure 4
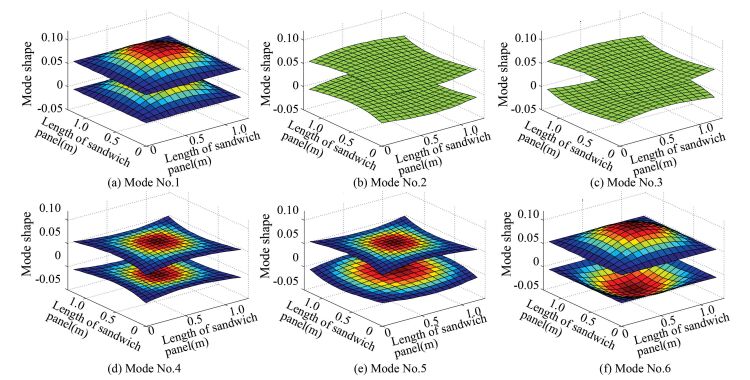Figure 4 Mode shape associated with wave number m=1, n=1 obtained by present model



The critical temperature of panel B calculated by the present model is 102.12 ℃, it matches well with the value 102.18 ℃ and 101.92 ℃, which obtained by Li^[18] and Nastran, respectively. The natural frequencies of panel B obtained by the present model, Li^[18] and Nastran under different temperatures are presented in Table 2.

表 2
Table 2 Comparison of natural frequencies with those obtained by Li and Nastran (Hz)

Mode No.ModelTemperature(℃)

0255075100

(1, 1)Present work235.11204.32167.97121.1733.91

Li^[18]235.10204.32168.00121.2634.37

Nastran234.90204.06167.65120.7232.22

(2, 1)Present work397.26361.72322.30272.66183.45

Li^[18]397.25361.73322.32272.78183.70

Nastran394.64358.88319.07272.03182.36

(1, 2)Present work443.18394.61339.16277.32223.46

Li^[18]443.16394.62339.22277.37223.55

Nastran442.97394.31338.73273.53218.70

(2, 2)Present work548.45496.66438.80372.05290.33

Li^[18]548.44496.68438.85372.14290.50

Nastran546.03493.91435.61368.18285.24

(3, 1)Present work573.55528.76479.92425.28362.62

Li^[18]573.55528.77479.84425.31362.68

Nastran564.30518.63468.54412.41344.90

(1, 3)Present work681.62615.35541.03454.72347.60

Li^[18]681.61615.37541.09454.84347.81

Nastran681.10614.54539.84452.98347.32



Table 2 Comparison of natural frequencies with those obtained by Li and Nastran



Table 2 shows that natural frequencies obtained by the present analysis are in good agreement with those calculated by Li^[18] and Nastran under different temperatures.

3.2 Validation for Vibration and Sound ResponseConsidering the unit transverse concentrated harmonic force imposed on the top face sheet of panel B at point (0.1 m, 0.1 m). The vibration response measurement point is identical to the exciting point. The panel is vibrating in the air medium with the density ρ₀=1.2 kg/m³ and the sound speed c₀=343 m/s. The sound pressure level observation point is (0.1 m, 0.1 m, 3 m). The comparison of the velocity and the sound pressure level obtained by the present analysis and those calculated by Li^[18] are shown in Fig. 5 and Fig. 6 under different temperatures. A good agreementbetween the results obtained by the present work and Li^[18] is observed whether there is the temperature load or not. It is because that the dilatational natural frequencies of panel B, which has little effect on the response below 1 000 Hz, are much higher than 1 000 Hz. For instance, the first order dilatational mode frequency is 9 447 Hz.

Figure 5
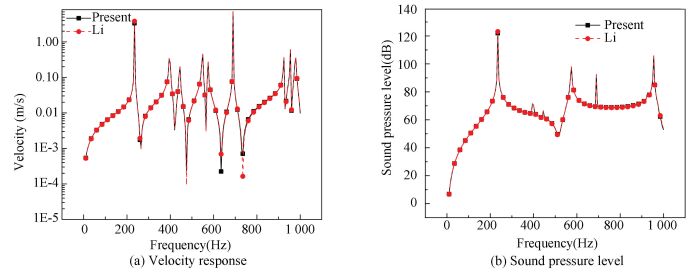Figure 5 Comparison of the response between the present analysis and Li's results (T=0 ℃)



Figure 6
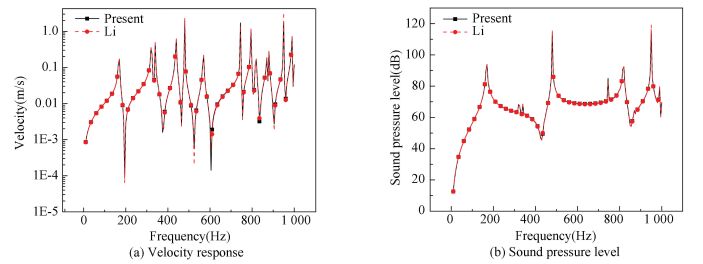Figure 6 Comparison of the response between the present analysis and Li's results (T=50 ℃)



All the above analyses indicate that the present model is available and effective for the calculation of the natural frequency, vibration and sound response of sandwich panels.

4 Numerical Results and DiscussionTwo simply supported sandwich panels C and D are investigated in detail in this section. The dimension of the two panels is 400 mm×300 mm with face sheet thickness 2 mm and core thickness 30 mm. The properties of panel C are assumed to be temperature independent. The material properties of the face sheet of panel C are E_f=68.9 GPa, μ_f=0.3, ρ_f=2 700 kg/m³, α_f=2.4×10^-6/℃, η_f=0.001 and the core material properties are E_c=2.4 MPa, μ_c=0.3, ρ_c=500 kg/m³, α_c=1.8×10^-7/℃, η_c=0.002. The face sheets of panel D are made of PEEK/IM7, and the temperature dependence of the viscoelastic properties of PEEK/IM7 is given in Table 3. The coefficient of thermal expansion and density of PEEM/IM7 are α₁=-0.15×10^-6/℃, α₂=26.57×10^-6/℃, ρ_f=1 290 kg/m³, respectively. The elastic modulus of the core of panel D is E_c=24 MPa, and other material properties are the same with the core of panel C. Panel C is used to investigate the effects of temperature on the natural frequencies and the effect of symmetric motion on the vibration and acoustic responses. Panel D is aimed to investigate the effects of temperature on the vibration and acoustic responses.

表 3
Table 3 Temperature dependence of the viscoelastic properties of PEEK/IM7^[22] Temperature(℃)E₁(GPa)E₂(GPa)G₁₂(GPa)μ₁₂η₁(10^-3)η₂(10^-3)η₆(10^-3)

0155.110.17.30.344.57.510.5

40154.710.07.10.345.27.711.5

80154.39.87.00.356.89.314.6



Table 3 Temperature dependence of the viscoelastic properties of PEEK/IM7^[22]



4.1 Effects of Temperature on Natural FrequenciesThe critical temperature of panel C is 51.57 ℃. Once the temperature exceeds the critical temperature, the responses calculated by the linear theory used in the present method are inaccurate. Therefore, the temperature load range is selected from 0 ℃ to 50 ℃. Assuming that the frequency ratio defined as γ=f_T/f₀, where f₀ is the natural frequency at 0 ℃, and f_T is the natural frequency with temperature load. The natural frequency ratios of the anti-symmetric and symmetric motions under different temperature loads are plotted in Fig. 7. As illustrated in Fig. 7 that the natural frequencies decrease with the increase of temperature while the mode shapes remain the same for both anti-symmetric and symmetric motions. The compressive thermal stresses induced by the high temperature cause the reduction of the stiffness of the panel, which lead to the natural frequencies decrease. For anti-symmetric motion, the fundamental frequency is much more sensitive to the variation of temperature since the buckling takes place for the first order mode in the first place as the temperature increase. For symmetric motion, the influence of temperature on the higher order mode (3, 2) is more obvious. This is attributable to the fact that the buckling temperature of the higher mode is lower than that of the lower order modes for symmetric motion.

Figure 7
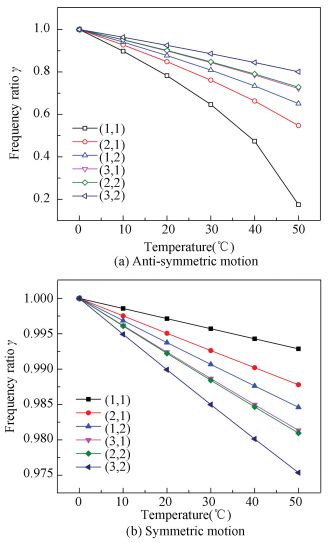Figure 7 Natural frequency ratio of sandwich panel under different temperatures



4.2 Effects of Symmetric Motion on Vibration and Sound ResponseIn order to evaluate the effect of symmetric motion on the vibration and sound response of sandwich panels, velocity and sound response of panel C only with anti-symmetric motion, only with symmetric motion and both the two motions taken into account are calculated and plotted in Fig. 8. The temperature is set to be 0 ℃.

Figure 8
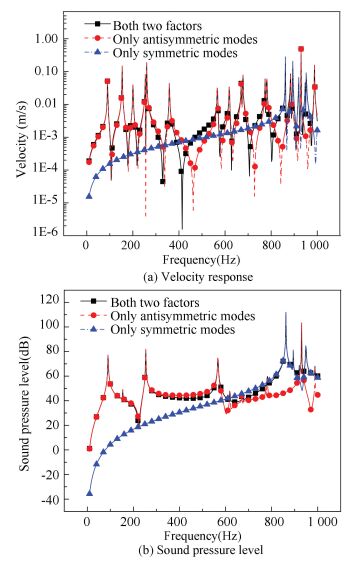Figure 8 Velocity and sound pressure level response due to different factors



As demonstrated in Fig. 8 that symmetric modes induce the anti-resonant frequencies which are close to the symmetric natural frequency float to the low frequency domain, while it has little effect on the anti-symmetric resonant frequencies. In addition, new response peaks occur at the natural frequencies of symmetric motion in velocity and sound pressure level response. Therefore, symmetric motion should be taken into consideration for sandwich panels with a soft, flexible core when calculate the vibration and sound response.

4.3 Effects of Temperature on Vibration and Sound ResponseTo explore the impacts of temperature on vibration and sound response, the displacement, velocity of the exciting point and sound pressure level of the observation point under different temperature loads for panel D are illustrated in Fig. 9. The points where the force imposed, vibration response measured and sound pressure observed are the same as the panel B. It is observed from Fig. 9 that the peaks of the response move leftward to the low frequency range and the value of the peaks decrease as the temperature increases. The high temperature softens the rigidity of the panel which reduces the natural frequencies. As consequence, all the response peaks float to the low frequency range.As the temperature rises, the damping loss factor of the panel increases^[22], which results in the vibration amplitude decreased at the resonant frequencies.

Figure 9
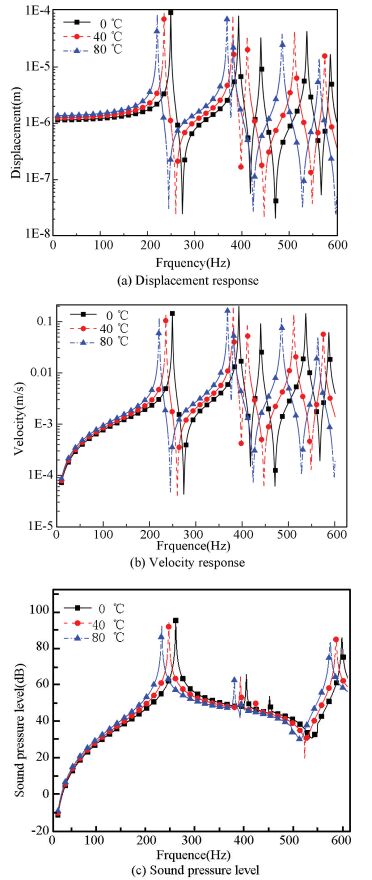Figure 9 Displacement, velocity and sound pressure level response under different thermal environments



5 Summary and ConclusionsThis paper focuses on the vibration and acoustic response of sandwich panels with flexible core under thermal environments. For this purpose, governing equations with both symmetric and anti-symmetric motions taken into account have been derived. Natural frequency, vibration and sound pressure level responses have been calculated and discussed in detail. The primary conclusions are presented as follows.

(1) The natural frequencies of both flexural mode and dilatational mode decrease with the rise of temperature. For flexural modes, the first-order natural frequency is more sensitive to the variation of temperature. However, thermal environment has great influence on the high order natural frequency for dilatational mode.

(2) Anti-resonant frequencies which close to the dilatational natural frequency will move to the low frequency range and new picks will appear at the dilatational natural frequencies when symmetric motions are considered in the calculation of vibration and sound response.

(3) The peaks of the velocity and sound pressure level responses remove to the low frequency domain as the temperature increases. The value of the peaks decreases with the rise of temperature due to the increase of damping loss factor.

(4) Both symmetric and anti-symmetric motions should be considered for sandwich panels with soft, flexible core when calculating vibration and sound response.


References
[1] Sayyad A S, Ghugal Y M. On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results. Composite Structures, 2015, 129: 177-201. DOI:10.1016/j.compstruct.2015.04.007 (0)

[2] Frostig Y, Baruch M, Vilnay O, et al. High-order theory for sandwich-beam behavior with transversely flexible core. Journal of Engineering Mechanics, 1992, 118(5): 1026-1043. DOI:10.1061/(ASCE)0733-9399(1992)118:5(1026) (0)

[3] Frostig Y. Buckling of sandwich panels with a flexible core—high-order theory. International Journal of Solids and Structures, 1998, 35(3-4): 183-204. DOI:10.1016/S0020-7683(97)00078-4 (0)

[4] Frostig Y, Phan C N, Kardomateas G A. Free vibration of unidirectional sandwich panels, Part Ⅰ: Compressible core. Journal of Sandwich Structures and Materials, 2013, 15(4): 377-411. DOI:10.1177/1099636213485518 (0)

[5] Phan C N, Frostig Y, Kardomateas G A. Free vibration of unidirectional sandwich panels, Part Ⅱ: Incompressible core. Journal of Sandwich Structures and Materials, 2013, 15(4): 412-428. DOI:10.1177/1099636213485520 (0)

[6] Oskooei S, Hansen J S. Higher-order finite element for sandwich plates. AIAA Journal, 2000, 38(3): 525-533. DOI:10.2514/2.991 (0)

[7] Nabarrete A, de Almeida S F M, Hansen J S. Sandwich-plate vibration analysis: Three-layer quasi-three-dimensional finite element model. AIAA Journal, 2003, 41(8): 1547-1555. DOI:10.2514/2.2106 (0)

[8] Frostig Y, Thomsen O T. High-order free vibration of sandwich panels with a flexible core. International Journal of Solids and Structures, 2004, 41(5-6): 1697-1724. DOI:10.1016/j.ijsolstr.2003.09.051 (0)

[9] Elmalich D, Rabinovitch O. A high-order finite element for dynamic analysis of soft-core sandwich plates. Journal of Sandwich Structures and Materials, 2012, 14(5): 525-555. DOI:10.1177/1099636212449841 (0)

[10] Matsunaga H. Free vibration and stability of angle-ply laminated composite and sandwich plates under thermal loading. Composite Structures, 2007, 77(2): 249-262. DOI:10.1016/j.compstruct.2005.07.002 (0)

[11] Jeyaraj P, Padmanabhan C, Ganesan N. Vibration and acoustic response of an isotropic plate in a thermal environment. Journal of Vibration and Acoustics, 2008, 130(5): 051005-1. DOI:10.1115/1.2948387 (0)

[12] Jeyaraj P, Ganesan N, Padmanabhan C. Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment. Journal of Sound and Vibration, 2009, 320(1-2): 322-338. DOI:10.1016/j.jsv.2008.08.013 (0)

[13] Jeyaraj P, Padmanabhan C, Ganesan N. Vibro-acoustic behavior of a multilayered viscoelastic sandwich plate under a thermal environment. Journal of Sandwich Structures and Materials, 2011, 13(5): 509-537. DOI:10.1177/1099636211400129 (0)

[14] Geng Q, Li Y. Analysis of dynamic and acoustic radiation characters for a flat plate under thermal environments. International Journal of Applied Mechanics, 2012, 4(3): 1250028. DOI:10.1142/S1758825112500287 (0)

[15] Geng Q, Li H, Li Y. Dynamic and acoustic response of a clamped rectangular plate in thermal environments: Experiment and numerical simulation. The Journal of the Acoustical Society of America, 2014, 135(5): 2674-2682. DOI:10.1121/1.4870483 (0)

[16] Geng Q, Li Y. Solutions of dynamic and acoustic responses of a clamped rectangular plate in thermal environments. Journal of Vibration and Control, 2016, 22(6): 1593-1603. DOI:10.1177/1077546314543730 (0)

[17] Liu Y, Li Y. Vibration and acoustic response of rectangular sandwich plate under thermal environment. Shock and Vibration, 2013, 20(5): 1011-1030. DOI:10.1155/2013/281723 (0)

[18] Li X, Yu K. Vibration and acoustic responses of composite and sandwich panels under thermal environment. Composite Structures, 2015, 131: 1040-1049. DOI:10.1016/j.compstruct.2015.06.037 (0)

[19] Li W, Li Y. Vibration and sound radiation of an asymmetric laminated plate in thermal environments. Acta Mechanica Solida Sinica, 2015, 28(1): 11-22. DOI:10.1016/S0894-9166(15)60011-8 (0)

[20] Zhou R, Crocker M J. Sound transmission characteristics of asymmetric sandwich panels. Journal of Vibration and Acoustics, 2010, 132(3): 031012-1. DOI:10.1115/1.4000786 (0)

[21] Smolenski C P, Krokosky E M. Dilational-mode sound transmission in sandwich panels. The Journal of the Acoustical Society of America, 1973, 54(6): 1449-1457. DOI:10.1121/1.1914444 (0)

[22] Melo J D D, Radford D W. Time and temperature dependence of the viscoelastic properties of CFRP by dynamic mechanical analysis. Composite Structures, 2005, 70(2): 240-253. DOI:10.1016/j.compstruct.2004.08.025 (0)