Yi Cao1,2,3,4, Hai Chen1,4, Youlei Qin1,4, Shuyi Ge1,4and Hui Zhou1,4
(1. School of Mechanical Engineering, Jiangnan University, Wuxi Jiangsu 214122, China;2. State Key Laboratory of Robotics and System, Harbin 150080, China;3. State Key Laboratory of Mechanical System and Vibration, Shanghai 200240, China;4. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi Jiangsu 214122, China)
Abstract:
Based on the screw theory and the driven-chain principle, a methodology of structural synthesis for fully-decoupled two-translational (2T) and two-rotational (2R) parallel mechanism is proposed by analyzing the characteristics of the input-output relations for fully-decoupled parallel mechanisms. Firstly, according to the desired kinematic characteristics of fully-decoupled parallel mechanisms, a method is proposed by virtue of screw theory to synthesize the desired forms for both the direct and the inverse Jacobian matrices. Secondly, according to the feature of the direct and the inverse Jacobian matrices, the effective screws, the actuated screws and the mobile un-actuated screws of each leg are established based on the reciprocal screw theory and all possible topology structures fulfilling the requirements are obtained. Finally, the desired fully-decoupled parallel mechanisms can be synthesized by using the structural synthesis rule and structural synthesis of fully-decoupled 2T2R parallel mechanisms can be obtained exploiting the abovementioned methodology. In particular, the direct Jacobian matrix of each synthesized fully-decoupled 2T2R parallel mechanism is a non-zero diagonal matrix throughout the entire workspace. Motors are mounted on each leg and each one of them actuates one degree-of-freedom (DoF) of the fully-decoupled parallel mechanism through a one-to-one velocity relation.
Key words: type synthesis fully-decoupled parallel mechanisms driven-chanin principle screw theory
DOI:10.11916/j.issn.1005-9113.2016.05.007
Clc Number:TP24
Fund:
Yi Cao, Hai Chen, Youlei Qin, Shuyi Ge, Hui Zhou. Type Synthesis of fully-Decoupled 2T2R Parallel Mechanisms Based on Driven-Chain Principle[J]. Journal of Harbin Institute of Technology, 2016, 23(5): 45-52. DOI: 10.11916/j.issn.1005-9113.2016.05.007.

Fund Sponsored by the National Natural Science Foundation of China (Grant No. 50905075), the Open Project of the State Key Laboratory of Robotics and System (Grant No. SKLRS-2016-KF-06), the Open Project of the State Key Laboratory of Mechanical System and Vibration of China (Grant No. MSV201407), the Open Project of Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology (Grant No. FM-201402) and the Research and the Innovation Project for College Graduates of Jiangsu Province (Grant No. SJZZ16-0212) Corresponding author Yi Cao, E-mail: caoyi@jiangnan.edu.cn Article history Received: 2015-06-04
Contents Abstract Full text Figures/Tables PDF
Type Synthesis of fully-Decoupled 2T2R Parallel Mechanisms Based on Driven-Chain Principle
Yi Cao1,2,3,4

 , Hai Chen1,4, Youlei Qin1,4, Shuyi Ge1,4, Hui Zhou1,4
, Hai Chen1,4, Youlei Qin1,4, Shuyi Ge1,4, Hui Zhou1,4 1. School of Mechanical Engineering, Jiangnan University, Wuxi Jiangsu 214122, China;
2. State Key Laboratory of Robotics and System, Harbin 150080, China;
3. State Key Laboratory of Mechanical System and Vibration, Shanghai 200240, China;
4. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi Jiangsu 214122, China
Received: 2015-06-04
fund: Sponsored by the National Natural Science Foundation of China (Grant No. 50905075), the Open Project of the State Key Laboratory of Robotics and System (Grant No. SKLRS-2016-KF-06), the Open Project of the State Key Laboratory of Mechanical System and Vibration of China (Grant No. MSV201407), the Open Project of Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology (Grant No. FM-201402) and the Research and the Innovation Project for College Graduates of Jiangsu Province (Grant No. SJZZ16-0212)
Corresponding author: Yi Cao, E-mail: caoyi@jiangnan.edu.cn
Abstract: Based on the screw theory and the driven-chain principle, a methodology of structural synthesis for fully-decoupled two-translational (2T) and two-rotational (2R) parallel mechanism is proposed by analyzing the characteristics of the input-output relations for fully-decoupled parallel mechanisms. Firstly, according to the desired kinematic characteristics of fully-decoupled parallel mechanisms, a method is proposed by virtue of screw theory to synthesize the desired forms for both the direct and the inverse Jacobian matrices. Secondly, according to the feature of the direct and the inverse Jacobian matrices, the effective screws, the actuated screws and the mobile un-actuated screws of each leg are established based on the reciprocal screw theory and all possible topology structures fulfilling the requirements are obtained. Finally, the desired fully-decoupled parallel mechanisms can be synthesized by using the structural synthesis rule and structural synthesis of fully-decoupled 2T2R parallel mechanisms can be obtained exploiting the abovementioned methodology. In particular, the direct Jacobian matrix of each synthesized fully-decoupled 2T2R parallel mechanism is a non-zero diagonal matrix throughout the entire workspace. Motors are mounted on each leg and each one of them actuates one degree-of-freedom (DoF) of the fully-decoupled parallel mechanism through a one-to-one velocity relation.
Key words: type synthesis fully-decoupled parallel mechanisms driven-chanin principle screw theory
1 IntroductionDuring the past more than two decades, parallel manipulator systems have become one of the research attentions in robotics. This popularity has been motivated by the fact that parallel manipulators possess some specific advantages in accuracy, rigidity, stiffness and load-carrying capacity, better dynamic performance, etc.over serial manipulators[1-2].Among them, the best-known parallel manipulator is Delta mechanism[3] which is widely used in practice. Meanwhile, the type synthesis of parallel mechanisms has obtained remarkable advance with contributions from many scholars generally based on group theory[4], screw theory[5], the single-opened-chain synthesis method[6], etc.
In the area of parallel mechanisms, the use of lower-mobility parallel mechanisms for many tasks requiring fewer than 6-DoF has drawn a lot of interests owing to the fact that it leads to fewer links and actuators. Developers can stand a good chance of reducing the costs of design and manufacturing. Strong coupling is a prominent feature of parallel mechanisms which makes the parallel mechanisms possess some special advantages over serial mechanisms. However it is the strong coupling that brings many difficulties, such as nonlinear relationship between input and output, complex workspace, difficulties in the analysis, trajectory planning and precision control, which restricts its application fields. Therefore, the type synthesis of fully-decoupled lower-mobility parallel mechanisms has become a new topic in this area and has captured researcher's attention [7-18].
As the authors are aware that most of reported work above has been deal with the type synthesis of fully-decoupled parallel mechanisms with three rotational DoF or three translational DoF, respectively, much lessen work has been reported for the topic of the type synthesis of fully-decoupled 2T2R parallel mechanism which is the main contribution of the present paper.
The organization of the present paper is as follows. Based on the screw theory and the driven-chain principle (the principle of each leg of parallel mechanism actuated by one motor), a methodology of structural synthesis for fully-decoupled 2T2R parallel mechanism is proposed by analyzing the characteristics of the input-output relations for fully-decoupled parallel mechanisms. Firstly, according to the expected kinematic characteristics of the fully-decoupled 2T2R parallel mechanism (rotate about X, Y axis and move along X, Y axis, respectively), a method is proposed by virtue of screw theory to synthesize the desired forms for both the direct and the inverse Jacobian matrices. Secondly, according to the feature of the direct and the inverse Jacobian matrices, the effective screws, the actuated screws and the mobile un-actuated screws of each leg of the fully-decoupled 2T2R parallel mechanism are established based on the reciprocal screw theory and all possible topology structures fulfilling the requirements are obtained. Finally, the desired fully-decoupled 2T2R parallel mechanism can be synthesized by using the structural synthesis rule and structural synthesis of fully-decoupled 2T2R parallel mechanism can be obtained exploiting the abovementioned methodology. In particular, the direct Jacobian matrix of each synthesized fully-decoupled 2T2R parallel mechanism is a non-zero diagonal matrix throughout the entire workspace. Motors are mounted on each leg and each one of them actuates one DoF of the fully-decoupled parallel mechanism through a one-to-one velocity relation.
2 Basic Theory2.1 The Screw TheoryIn Ref. [19], it shows that a unit screw $ can be defined by a pair of vectors $=(S; S0). S a unit vector is called the original part of $ specifying the direction of the screw axis, S0 is called the dual part of $:
${{\boldsymbol{S}}_{0}}=\boldsymbol{r}\text{ }\!\!\times\!\!\text{ }\boldsymbol{S}+h\boldsymbol{S}$ (1)
where r is the position vector of any point on the screw axis in terms of a reference coordinate system and h is the pitch of $. $ can also be expressed in six plucker coordinates (L, M, N; P, Q, R). We call the screw a twist if it represents an instantaneous motion of a rigid body. We call the screw a wrench if it represents a force and a coaxial couple acting on a rigid body.
2.2 The Reciprocal ScrewIf the two screws $1=(S; S0) and $2=(Sr; S0r) can satisfy the condition:
${{\boldsymbol{\mathit{$}}}_{1}}^{\text{ }\!\!{}^\circ\!\!\text{ }}{{\boldsymbol{\mathit{$}}}_{2}}\text{=}S\cdot S_{0}^{r}+{{S}^{r}}\cdot {{S}_{0}}=0$ (2)
The screw $1 and $2
2.3 The Effective ScrewThe effective screw expresses the force or coaxial couple acting on the rigid body by the driver.When $i=(S; S0)=(l, m, n; p, q, r), it represents a force, while when $i=(0;S)=(0, 0, 0; l, m, n), it indicates a coaxial couple acting on the rigid body. The effective screw is reciprocal to all the twists of the leg of parallel mechanisms with the exception of the actuated one [20].
2.4 The Constraint ScrewWhen the screw $ is used to describe the prescribed motion of the moving platform of parallel mechanisms, the constraint screw system can be obtained by calculating its reciprocal screw, the constraint screw system represents the restricted DoF of the moving platform of parallel mechanisms.The detailed geometry condition of the constraint screw system and the restricted DoF refer to Ref. [19].
3 Instantaneous Kinematics Analysis of the Parallel MechanismThis paper will only discuss the type synthesis of fully-decoupled 2T2R parallel mechanism. Without loss of generality, it can be assumed that the 2T2R parallel mechanism moves along X, Y axes and rotates about X, Y axes. Then, the instantaneous kinematics of the mechanism can be determined by using the reciprocal screw theory. If $ji represents the twist associated with the jth joint of the ith (i=1, 2, 3, 4) leg and
$\boldsymbol{T}=\sum\limits_{j=1}^{{{F}_{i}}}{{{{\dot{q}}}_{ji}}{{\boldsymbol{\mathit{$}}}_{ji}}, i=1, 2, 3, 4}$ (3)
where T is the velocity vector of the moving platform of parallel mechanisms; Fi is the connectivity of the ith leg. If $ai is the effective screw of the ith leg, it is a screw that is reciprocal to all the twists of the leg with the exception of the actuated one, taking the reciprocal product of both sides of Eq. (3) with $ai yields:
$\boldsymbol{\mathit{$}}_{\text{ai}}^{\text{T}}\hat{T}=\boldsymbol{\mathit{$}}_{\text{ai}}^{\text{T}}{{{\hat{\boldsymbol{\mathit{$}}}}}_{1i}}{{{\dot{q}}}_{1i}}, i=1, 2, 3, 4$ (4)
where superscript T indicates the thanspose matrix of a matrix. When the first joint (base-mounted) is assumed to be the actuated one, Eq. (4) can be written in matrix form as:
$\begin{array}{l}\left[\begin{array}{l}\boldsymbol{\mathit{$}}_{{\rm{a1}}}^{\rm{T}}\\\boldsymbol{\mathit{$}}_{{\rm{a2}}}^{\rm{T}}\\\boldsymbol{\mathit{$}}_{{\rm{a3}}}^{\rm{T}}\\\boldsymbol{\mathit{$}}_{{\rm{a4}}}^{\rm{T}}\end{array} \right]\left[\begin{array}{l}\boldsymbol{v}\\\boldsymbol{w}\end{array} \right] = \\\left[{\begin{array}{*{20}{c}}{\boldsymbol{\mathit{$}}_{{\rm{a1}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{11}}}&0&0&0\\0&{\boldsymbol{\mathit{$}}_{{\rm{a2}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{12}}}&0&0\\0&0&{\boldsymbol{\mathit{$}}_{{\rm{a3}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{13}}}&0\\0&0&0&{\boldsymbol{\mathit{$}}_{{\rm{a4}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{14}}}\end{array}} \right]\left[\begin{array}{l}{{\dot q}_{11}}\\{{\dot q}_{12}}\\{{\dot q}_{13}}\\{{\dot q}_{14}}\end{array} \right]\end{array}$ (5)
where ω=[ωx, ωy, ωz] is the angular velocity of the moving platfrom of paralel mechanisms and v=[vx, vy, vz] the linear velocity of any point (generally, the center of the moving platfrom) on the moving platform. Provided that the leg constraint screw system restricts the translational and rotational DoF of the moving platform around Z axis, namely the Z components of ω and v are always equal to zero. It follows that these comments, together with the corresponding ones of $ai (i=1, 2, 3, 4) can be laid aside in the left-hand of Eq. (5) without affecting the validity of the expression, which can thus be put in the form:
${\boldsymbol{J}_{{\rm{dir}}}}\boldsymbol{\hat t} = {\boldsymbol{J}_{{\rm{inv}}}}\boldsymbol{\dot q}$ (6)
$\boldsymbol{\hat t} = \left[\begin{array}{l}{v_x}\\{v_y}\\{w_x}\\{w_y}\end{array} \right], \boldsymbol{\dot q} = \left[\begin{array}{l}{{\dot q}_{11}}\\{{\dot q}_{12}}\\{{\dot q}_{13}}\\{{\dot q}_{14}}\end{array} \right]$ (7)
${\boldsymbol{J}_{{\rm{dir}}}} = \left[\begin{array}{l}\boldsymbol{s}_{{\rm{a1}}}^{\rm{T}}\\\boldsymbol{s}_{{\rm{a2}}}^{\rm{T}}\\\boldsymbol{s}_{{\rm{a3}}}^{\rm{T}}\\\boldsymbol{s}_{{\rm{a4}}}^{\rm{T}}\end{array} \right]$ (8)
${\boldsymbol{J}_{{\rm{inv}}}} = \left[{\begin{array}{*{20}{c}}{\boldsymbol{\mathit{$}}_{{\rm{a1}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}} }_{11}}}&0&0&0\\0&{\boldsymbol{\mathit{$}}_{{\rm{a2}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{12}}}&0&0\\0&0&{\boldsymbol{\mathit{$}}_{{\rm{a3}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{13}}}&0\\0&0&0&{\boldsymbol{\mathit{$}}_{{\rm{a4}}}^{\rm{T}}{{\boldsymbol{\mathit{\hat$}}}_{14}}}\end{array}} \right]$ (9)
where
If the Jinv is not a singular matrix, that:
$\boldsymbol{\dot q} = \boldsymbol{J}_{{\rm{inv}}}^{{\rm{ - 1}}}{\boldsymbol{J}_{{\rm{dir}}}}\boldsymbol{\hat t}$ (10)
where J is the Jacobian matrix of the mechanism and
$\boldsymbol{J} = \boldsymbol{J}_{{\rm{inv}}}^{{\rm{ - 1}}}{\boldsymbol{J}_{{\rm{dir}}}}$ (11)
In order to synthesize fully-decoupled 2T2R parallel mechanism, the Jacobian matrix J dentoed by Eq. (11) should be a non-zreo diagonal matrix, therefore, the direct Jabocian matrix Jdir by Eq. (8) should be a diagonal matrix since the inverse Jacobian matrix Jinv denoted by Eq. (9) has always satisfied the requirement of being a diagonal matrix.
4 Type Synthesis Theory for Fully-Decoupled 2T2R Parallel MechanismsAs described in Section 3, if the inverse Jacobian matrix is a non-zreo diagonal matrix, the mechanism must be fully decoupled. Based on this conclusion, a method will be proposed by virtue of screw theory to synthesize desired forms for both the direct and the inverse Jacobian matrices.
Since the Jacobian matrix is related with the effective screws and actuated screws on the corresponding leg, the desired form of the effective screw and the actuated screw should be determined to construct a non-zero diagonial matrix for the synthesis of fully-decoupled parallel mechanisms. Due to the fact that the actuated screw varies with the configuration of the moving platform, hence, all motors are required to be mounted on the base platform to ensure that the actuate screw will not vary with the configuration of the moving platform of parallel mechanisms.
Zeng et al.[21] pointed out that for fully-decoupled parallel mechanisms, when the effective screw is a force, the actuated joint can be a prismatic pair or a parallel 2R revolute pair and when the effective screw stands for a coaxial couple, the actuated joint should be a revolute pair. Based on the conclusion, the type synthesis of fully-decoupled 2T2R parallel mechanism can be accomplished by the driven-chain principle, which can described by the following:
(a) Based on the driven-chain principle, the output of each leg of the 2T2R parallel mechanism should be determined and the effective screw of the driver in the leg can be constructed to satisfy the requirements that both the direct and inverse Jacobian matrix should be a non-zero diagonal matrix.
(b) Based on the analysis of the effective screw of each leg, the actuated joint can be detemined that when the effective screw is a force, the actuated joint can be a prismatic pair or a parallel 2R revolute pair and when the effective screw stands for a coaxial couple, the actuated joint should be a revolute pair.
(c) According to the reciprocal screw theory, the twist of the leg of the fully-decoupled 2T2R parallel mechanism with the exception of the actuated joint can be deduced. The effective screws, the actuated screws and the mobile un-actuated screws of each leg are established and all possible structures of each leg of the parallel mechanism can be synthsized according to different connectivity of each leg. Repeat Steps (a)-(c) until that structures of each leg of the 2T2R parallel mechanism have been constructed successfully.
(d) Based on the structural synthesis rule and the rotational conditons for fully-decoupled parallel mechanisms proposed in Ref. [15], four legs can be selected from Step (c) and are connected to the moving platform and base platform, the desired fully-decoupled 2T2R parallel mechanism can be realized.
Both the direct and the inverse Jacobian matrix is a non-zero diagonal matrix, hence the Jacobian matrix is a non-zero diagonal matrix which indicates the parallel mechanism to be synthesized within this paper is fully-decoupled.Moreover, a one-to-one correspondece exists between the actuated joint space and the output space of the moving platform since that each DoF of the moving platform is drived by one motor for each leg.
5 Design of the Architectures for Four LegsWithout loss of generality, it can be assumed that the 2T2R parallel mechanism to be synthesized in this paper moves along X, Y axes and rotates about X, Y axes. In the following section, we can assume that the first and the second leg provide the actuation to the platform translation along X, Y axes and the third and fourth leg provide the actuation rotation around X, Y axes. As the kinematic characteristics of parallel mechanisms is the intersection set of the kinematic characteristics of each leg constituting a parallel mechanism, therefore, each leg should include the kinematic characteristics of the moving platform, the connectivity of each leg should be at least 4. In order to synthesize the fully-decoupled 2T2R parallel mechanism, four legs should be constructed firstly, which will be interpreted in the following.
5.1 The First LegThe first leg provides direct actuation to the platform translation along the X-axis. Since [Jdir]11 has to be the only non-zero element in the first row of the direct Jacobian matrix, Jdir, so $a1must has the following form:
${\boldsymbol{\mathit{$}}_{a1}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&0&{{r_1}}\end{array}} \right]$ (12)
That is to say, it must be a screw of zero pitch parallel with the X-direction. In this case, according to the analysis described in Section 4, there are three types of the actuated screw:
$\begin{array}{l}a.\;\;\;\;{\boldsymbol{\mathit{$}}_{q11}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&1&0&0\end{array}} \right], h = \infty \\b.\;\;\;\;\;{\boldsymbol{\mathit{$}}_{q12}} = \left[{\begin{array}{*{20}{c}}0&1&0&;&{{d_{12}}}&0&{{f_{12}}}\end{array}} \right], h = 0\\c.\;\;\;\;\;{\boldsymbol{\mathit{$}}_{q13}} = \left[{\begin{array}{*{20}{c}}0&0&1&;&{{d_{13}}}&{{e_{13}}}&0\end{array}} \right], h = 0\end{array}$ (13)
Substituting Eq.(13) into Eq.(9), it will turn out:
$\begin{array}{l}a.\;\;\;{\left[{{\boldsymbol{J}_{\rm{v}}}} \right]_{11}} = {\boldsymbol{\mathit{$}}_{{\rm{a1}}}}^{\rm{^\circ }}{\boldsymbol{\mathit{$}}_{{\rm{q}}11}} = 1\\b.\;\;\;{\left[{{\boldsymbol{J}_{\rm{v}}}} \right]_{11}} = {\boldsymbol{\mathit{$}}_{{\rm{a1}}}}^{\rm{^\circ }}{\boldsymbol{\mathit{$}}_{{\rm{q}}12}} = {d_{12}}\\c.\;\;\;{\left[{{\boldsymbol{J}_{\rm{v}}}} \right]_{11}} = {\boldsymbol{\mathit{$}}_{{\rm{a1}}}}^{\rm{^\circ }}{\boldsymbol{\mathit{$}}_{{\rm{q}}13}} = {d_{13}} + {r_1}\end{array}$
where [Jv]11 is the element of the inverse Jacobian matrix Jinv in the 1st row and the 1st column. Since d12, d13 and r1 are variables that associated with the origin of the coordinate system, if d12 and d13+r1 can be kept to be non-zero, then the corresponding three elememts [Jv]11 in Jinv are non-zero. The twist of the first leg of the fully-decoupled 2T2R parallel mechanism with the exception of the actuated screw can be deduced using the reciprocal screw theory. It can be proved that the only screw that belongs to such a complex have three categories, that is:
(a) Screw system with finite pitch whose direction is parallel to X-axis, the dimension of such a screw system is a maximum of 3 and a minimum of 1.
(b) Screw system with infinite pitch lying in arbitrary planes perpendicular to X-axis, the dimension of the screw system is a maximum of 2, and the direction in the leg is not parallel with each.
(c) Screw system with zero pitch intersecting with $a1. Its dimension is at least 1 and the direction is parallel to Y-axis.
5.1.1 The actuated pair, a prismatic joint along X-axis directionWhen the actuated pair is a prismatic joint along X-axis, there is:
$\begin{array}{l}{\boldsymbol{\mathit{$}}_{{\rm{a1}}}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&0&{{r_1}}\end{array}} \right], h = 0\\{\boldsymbol{\mathit{$}}_{{\rm{q11}}}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&1&0&0\end{array}} \right], h = \infty \end{array}$
According to Ref. [22], each leg should include the kinematic characteristics of parallel mechanism, and the connectivity of each leg must be at least 4. For the selected actuated pair, active un-actuated pairs must be chosen from the above set and all possible structures for each leg can be enumerated according to different connectivity of each leg. The detailed structures of the leg for the first category are shown in Table 1. In Table 1, T represents the prismatic joint, R the revolute joint; T and R denotes the acutated joint and the subscript; X, Y and Z indicates the axial direction, respectively. For simplicity of the structure of each leg, the axial direction of two adjacent pairs is assumed to be parallel or perpendicular with each other.
表 1
The first category42T2RTXTYRXRY
53T2RTXTYTZRXRY
2T3RTXTZRX1RX2RY; TXTYRX1RX2RY; TXTYRXRY1RY2
1T4RTXRX1RX2RX3RY; TXRX1RX2RY1RY2
The second category52T3RRY1RY2TYTZRX
1T4RRY1RY2TZRX1RX2; RY1RY2RY3TYRX; RY1RY2TYRX1RX2
5RRY1RY2RY3RX1RX2; RY1RY2RX1RX2RX3
The third category51T4RRZ1RZ2TYRXRY
5RRZ1RZ2RZ3RXRY
62T4RRZ1RZ2TYTZRXRY
1T5RRZ1RZ2RZ3TZRXRY; RZ1RZ2TZRX1RX2RY
RZ1RZ2TYRX1RX2RY; RZ1RZ2TYRXRY1RY2
6RRZ1RZ2RZ3RX1RX2RY; RZ1RZ2RZ3RXRY1RY2
RZ1RZ2RX1RX2RX3RY; RZ1RZ2RX1RX2RY1RY2
Table 1 Possible architectures of the first leg
5.1.2 The actuated pair, a revolute joint around Y-axis directionWhen the actuated pair is a revolute joint around Y-axis direction, there is:
$\begin{array}{l}{\boldsymbol{\mathit{$}}_{{\rm{a1}}}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&0&{{r_1}}\end{array}} \right], h = 0\\{\boldsymbol{\mathit{$}}_{{\rm{q12}}}} = \left[{\begin{array}{*{20}{c}}0&1&0&;&{{d_{12}}}&0&{{f_{12}}}\end{array}} \right], h = 0\end{array}$
When the actuated joint is a revolute pair, the connectivity of the leg should be at least 5, and the detailed structures of the leg for the second category are also shown in Table 1.
5.1.3 The actuated pair, a revolute joint around Z-axis directionWhen the actuated pair is a revolute joint around Z-axis, there is:
$\begin{array}{l}{\boldsymbol{\mathit{$}}_{{\rm{a1}}}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&0&{{r_1}}\end{array}} \right], h = 0\\{\boldsymbol{\mathit{$}}_{{\rm{q13}}}} = \left[{\begin{array}{*{20}{c}}0&0&1&;&{{d_{13}}}&{{e_{13}}}&0\end{array}} \right], h = 0\end{array}$
Similarily, the detailed structures of the first leg for the third category are shown in Table 1.
5.2 The Second LegThe second leg provides direct actuation to the platform translation along Y-axis. Similar process described in Subsection 5.1 can be explioted to the construction of the second leg, firstly:
${\boldsymbol{\mathit{$}}_{{\rm{a2}}}} = \left[{\begin{array}{*{20}{c}}0&1&0&;&0&0&{{r_2}}\end{array}} \right]$
Three types of actuated screw are:
$\begin{array}{l}a.\;\;\;\;{\boldsymbol{\mathit{$}}_{q21}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&0&1&0\end{array}} \right], h = \infty \\b.\;\;\;\;\;{\boldsymbol{\mathit{$}}_{q22}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&{{e_{22}}}&{{f_{22}}}\end{array}} \right], h = 0\\c.\;\;\;\;\;{\boldsymbol{\mathit{$}}_{q23}} = \left[{\begin{array}{*{20}{c}}0&0&1&;&{{d_{23}}}&{{e_{23}}}&0\end{array}} \right], h = 0\end{array}$
In the same way, Table 2 shows all possible leg architectures of the second leg.
表 2
The first category42T2RTYTXRYRX
53T2RTYTXTZRYRX
2T3RTYTZRY1RY2RX; TYTXRY1RY2RX; TYTXRYRX1RX2
1T4RTYRY1RY2RY3RX; TYRY1RY2RX1RX2;
The second category52T3RRX1RX2TXTZRY
1T4RRX1RX2TZRY1RY2; RX1RX2RX3TXRY; RX1RX2TXRY1RY2
5RRX1RX2RX3RY1RY2; RX1RX2RY1RY2RY3
The third category51T4RRZ1RZ2TXRYRX
5RRZ1RZ2RZ3RYRX
62T4RRZ1RZ2TXTZRYRX
1T5RRZ1RZ2RZ3TZRYRX; RZ1RZ2TZRY1RY2RX;
RZ1RZ2TXRY1RY2RX; RZ1RZ2TXRYRX1RX2
6RRZ1RZ2RZ3RY1RY2RX; RZ1RZ2RZ3RYRX1RX2;
RZ1RZ2RY1RY2RY3RX; RZ1RZ2RY1RY2RX1RX2
Table 2 Possible architectures of the second leg
5.3 The Third LegThough, the fully-decoupled 2T2R parallel mechanism has two rotational DoFs, based on the driven-chain principle, the third leg only offers the direct actuation to the platform rotation around X-axis, thereby $a3can be written as follwos:
${\boldsymbol{\mathit{$}}_{{\rm{a3}}}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&1&0&0\end{array}} \right]$ (14)
Assuming that the actuated screw of the actuated pair is $q3=[a3, b3, c3; d3, e3, f3], the actuated screw may lead the moving platform rotating around Y and Z axies when b3≠0, c3≠0, which is not the desired kinematic characteristics of the parallel mechanism, hence, $q3 should only has the following form:
${\boldsymbol{\mathit{$}}_{{\rm{q3}}}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&{{e_3}}&{{f_3}}\end{array}} \right]$ (15)
Substituting Eqs. (14) and (15) into Eq. (9) turns out:
${\left( {{\boldsymbol{J}_{\rm{v}}}} \right)_{33}} = {\boldsymbol{\mathit{$}}_{{\rm{a3}}}}^{\rm{^\circ }}{\boldsymbol{\mathit{$}}_{{\rm{q3}}}} = 1$
Clearly, [Jv]33 the element of the inverse Jacobian matrix Jinv in the 3rd row and the 3rd column, satisfy the condition of non-zero, thereby:
$\begin{array}{l}{\boldsymbol{\mathit{$}}_{{\rm{a3}}}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&1&0&0\end{array}} \right], h = \infty \\{\boldsymbol{\mathit{$}}_{{\rm{q3}}}} = \left[{\begin{array}{*{20}{c}}1&0&0&;&0&{{e_3}}&{{f_2}}\end{array}} \right], h = 0\end{array}$
Similarly, the twist of the third leg of the fully-decoupled 2T2R parallel mechanism with the exception of the actuated screw denoted by Eq. (15) can be deduced using the reciprocal screw theory. Further inspection shows that the only screw system that belongs to such a complex have two categories:
(a) Screw system with infinite pitch, whose direction can be arbitrary, the maximal dimension of such a screw system is up to 3, the minimal is 2 and the direction of any two screws in the screw system is not parallel each other.
(b) Screw system with zero pitch which should not only intersect with but also perpendicular to $a3. Its dimension is at least 1 and the direction is parallel to Y-axis.
Table 3 shows all possible leg architectures that result from previous considerations.
表 3
42T2RRXTXTYRY
53T2RRXTXTYTZRY
2T3RRXTYTZRY1RY2; RX1RX2TXTZRY; RX1RX2TXTYRY; RXTXTYRY1RY2
1T4RRX1RX2TZRY1RY2; RX1RX2TYRY1RY2; RXTYRY1RY2RY3; RX1RX2RX3TXRY; RX1RX2TXRY1RY2
5RRX1RX2RX3RY1RY2; RX1RX2RY1RY2RY3
Table 3 Possible architectures of the third leg
5.4 The Fourth LegThe fourth leg offers the direct actuation to the platform rotation around Y-axis. Similar process pursued in Subsection 5.3 can be explioted to the construction of the fourth leg, firstly:
$ \begin{array}{l}{\boldsymbol{\mathit{$}}_{{\rm{a4}}}} = \left[{\begin{array}{*{20}{c}}0&0&0&;&0&1&0\end{array}} \right], h = \infty \\{\boldsymbol{\mathit{$}}_{{\rm{q3}}}} = \left[{\begin{array}{*{20}{c}}0&1&0&;&{{d_4}}&0&{{f_4}}\end{array}} \right], h = 0\end{array} $
In the same way, Table 4 shows all possible leg architectures of the fourth leg.
表 4
42T2RRYTYTXRX;
53T2RRYTYTXTZRX
2T3RRYTXTZRX1RX2; RY1RY2TYTZRX; RY1RY2TYTXRX; RYTYTXRX1RX2
1T4RRY1RY2TZRX1RX2; RY1RY2TXRX1RX2; RYTXRX1RX2RX3; RY1RY2RY3TYRX; RY1RY2TYRX1RX2
5RRY1RY2RX1RX2RX3; RY1RY2RY3RX1RX2
Table 4 Possible architectures of the fourth leg
6 Type Synthesis for Fully-Docoupled 2T2R Parallel MechanismsAs described in Section 5 that all possible architectures of four legs constituting a fully-decoupled 2T2R parallel mechanism have been constructed successfully, each leg provides one independent actuation to the platform, respectively. Therefore, the type synthesis of fully-decoupled 2T2R parallel mechanism can be performed by the combination of the four synthesized legs according the following structural synthesis rule:
(a) There is only one leg whose connectivity is 4 in the fully-decoupled 2T2R parallel mechanism, and the rest three legs should be selected which can guarantee that it must have three-dimensional translational kinematic characteristics.
(b) One point to be noted is that the leg architectures of the third category in Tables 1-2 with connectivity 5, it can be proved these architecutres are all equivalent to the architecture, TXTYRXRY, by using the linear dependency of screws [5].
In order to demonstrate the applicability of the type synthesis methodology for fully-decoupled 2T2R parallel mechanism, a fully-decoupled 2T2R parallel mechanism will be synthesized and the Jacobian matrix of the parallel mechanism will be deduced to valid the correctness of the decoupling feature of the parallel mechanism synthesized.
A fully-decoupled 2T2R parallel mechanism is shown in Fig. 1, in which the type of first leg is TXTYRXRY, and the second is the type of RZ1RZ2TXRY1RY2RX, and the third is RX1RX2TZRY1RY2 and the fourth is RY1RY2RY3RX1RX2. Four legs respectively provides the direct actuation to the moving platform translating along X, Y axes, rotating around X, Y axes.
Figure 1
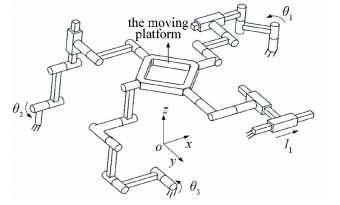 Figure 1 A fully-decoupled 2T2R parallel mechanism
Figure 1 A fully-decoupled 2T2R parallel mechanism In order to deduce the Jacobian matrix, a fixed reference system O-xyz is attached to the base platform, where O is the geometric center of the base platform. The corresponding input and output parameters of the mechanism are as follows. The symbol l1 actuated by a prismatic joint indicates the displacement of the first leg along x-axis, θ1 drived by a revolute pair denotes the rotation angle for the second leg around z-axis, θ2 drived by a revolute pair represents the rotation angle for the third leg around x-axis, θ3 drived by a revolute pair is the rotation angle for the fourth leg around y-axis, while the output parameters of the parallel mechanism is represented by the position denoted by (x, y) of the moving platform and orientation denoted by (α, β). Owing to space limitations, the detailed kinematic analysis of the mechanism will not presented here, the following relationship between the input and output paramenters should be satisfied:
$\left\{ \begin{array}{l}x = {l_1}\\y = L\left( {\sin \left( {180 - \gamma } \right) - \sin \left( {180 - \gamma - {\theta _1}} \right)} \right)\\\alpha = {\theta _2}\\\beta = {\theta _3}\end{array} \right.$ (16)
where L is the length of the link connected to the actuated pair, θ1, on second leg and γ is the initial rotation angle, as shown in Fig. 2.
Figure 2
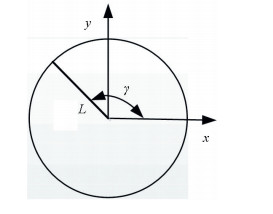 Figure 2 The input analysis of the mechanism around y-axis
Figure 2 The input analysis of the mechanism around y-axis The velocity of the end-effector of parallel mechanisms and the velocity of the driver can always be expressed as:
$\boldsymbol{\dot X} = \boldsymbol{J\dot q}$
where
$\left\{ \begin{array}{l}x' = l{'_1}\\y' = - L\cos \left( {\gamma + {\theta _1}} \right)\theta {'_1}\\\alpha ' = \theta {'_2}\\\beta ' = \theta {'_3}\end{array} \right.$ (17)
Eq.(17) can be expressed in a matrix form, that is:
$\left[\begin{array}{l}x'\\y'\\\alpha '\\\beta '\end{array} \right] = \left[{\begin{array}{*{20}{c}}1&0&0&0\\0&{-L\cos \left( {\gamma + {\theta _1}} \right)}&0&0\\0&0&1&0\\0&0&0&1\end{array}} \right] \cdot \left[\begin{array}{l}l{'_1}\\\theta {'_1}\\\theta {'_2}\\\theta {'_3}\end{array} \right]$
Hence,
$J = \left[{\begin{array}{*{20}{c}}1&0&0&0\\0&{-L\cos \left( {\gamma + {\theta _1}} \right)}&0&0\\0&0&1&0\\0&0&0&1\end{array}} \right]$ (18)
Obviously, the Jacobian matrix J denoted by Eq. (18) is an non-zero diagonal matrix with the exception of the special case when cos(γ+θ1)=0. Actually, the special case cos(γ+θ1)=0 should be avoided and will be excluded from the workspace in practice due to the fact the mechanism is in singular configuration. Therefore, the parallel mechanism is fully decoupled throughout the entire workspace which also validates the correctness of the methodology of the type synthesis for fully-decoupled 2T2R parallel mechanism.
7 ConclusionsThis paper mainly addresses the type synthesis of fully-decoupled 2T2R parallel mechanism and conclusions of the present paper can be drawn as follows:
(1) Within this paper, a methodology of type synthesis for fully-decoupled 2T2R parallel mechanism is proposed based on screw theory and driven-chain principle, moreover, the type synthesis of 2T2R parallel mechanism is performed.
(2) Based on the kinematic characteristics analysis of the input-output relations for fully-decoupled parallel mechanisms, both the direct and inverse matrixes for fully-decoupled 2T2R parallel mechanism are constructed, which provides underlying theoretical grounds for the type synthesis of four legs of the 2T2R parallel mechanism.
(3) All possible topology architectures of four legs with 2T2R parallel mechanism are proposed by means of reciprocal screw theory, moreover, the structural synthesis rule of type synthesis is given.
(4) The Jacobian matrix of a synthesized 2T2R parallel mechanism is deduced to demonstrate the decoupling feature of the parallel mechanism, which also validates the correctness of the methodology of the type synthesis for fully-decoupled 2T2R parallel mechanism.
References
[1]Meng Xiangdun, Gao Feng, Wu Shengfu. Type synthesis of parallel robotic mechanisms: Framework and brief review.Mechanism and Machine Theory, 2014, 78(8): 177-186.DOI:10.1016/j.mechmachtheory.2014.03.008(
 0)
0)[2]Arata J. Parallel mechanisms in haptics.Journal of the Robotics Society of Japan, 2012, 30(2): 144-147.DOI:10.7210/jrsj.30.144(
 0)
0)[3]Feng Lihang, Zhang Weigong, Gong Zongyang. Developments of Delta-like parallel manipulators-a review.Robot, 2014, 36(3): 375-384.(
 0)
0)[4]Hervé J M. The mathematical group structure of the set of displacements.Mechanism and Machine Theory, 1994, 29(1): 73-81.DOI:10.1016/0094-114X(94)90021-3(
 0)
0)[5]Huang Zhen, Li Qinchuan. General methodology for type synthesis of lower-mobility symmetrical parallel manipulators and several novel manipulators.International Journal of Robotics Research, 2002, 21(2): 131-145.DOI:10.1177/027836402760475342(
 0)
0)[6]Yang Tingli. Topology Structure Design of Robot Mechanisms.Beijing: China Machine Press, 2004.(
 0)
0)[7]Gong Jinliang, Zhang Yanfei, Gao Feng. Decoupling characteristics of the parallel mechanism.China Mechanical Engineering, 2006, 17(14): 1509-1512.(
 0)
0)[8]Glazunov V. Design of decoupled parallel manipulators by means of the theory of screws.Mechanism and Machine Theory, 2010, 45(2): 239-250.DOI:10.1016/j.mechmachtheory.2009.09.003(
 0)
0)[9]Carricato M, Parenti-Castelli V. A family of 3-DoF translational parallel manipulators.ASME Journal of Mechanical Design, 2003, 125(2): 302-307.DOI:10.1115/1.1563635(
 0)
0)[10]Gogu G. Structural synthesis of fully-isotropic translational parallel robots via theory of linear transformations.European Journal of Mechanics A/Solids, 2004, 23(6): 1021-1039.DOI:10.1016/j.euromechsol.2004.08.006(
 0)
0)[11]Kong Xianwen, Gosselin C M. Kinematics and singularity analysis of a novel type of 3-CRR 3-DoF translational parallel manipulator.The International Journal of Robotics Research, 2002, 21(9): 791-798.DOI:10.1177/02783649020210090501(
 0)
0)[12]Kong Xianwen, Gosselin C M. Type synthesis of input-output decoupled parallel manipulators.Transactions of the Canadian Society for Mechanical Engineering, 2004, 28(2): 185-196.(
 0)
0)[13]Li Weiming, Gao Feng, Zhang Jianjun. R-CUBE a decoupled parallel manipulator only with revolute joints.Mechanism and Machine Theory, 2005, 40(4): 467-473.DOI:10.1016/j.mechmachtheory.2004.09.001(
 0)
0)[14]Zhao Y, Liu J F, Huang Z. A force analysis of a 3-RPS parallel mechanism by using screw theory.Robotica, 2011, 29(7): 959-965.DOI:10.1017/S0263574711000129(
 0)
0)[15]Zeng Daxin, Huang Zhen. Type synthesis of the rotational decoupled parallel mechanism based on screw theory.Scientia Sinica Techologica, 2011, 54(4): 998-1004.(
 0)
0)[16]Zeng Daxin, Hu Zhitao, Hou Yulei. Type synthesis of 2R1T decoupled parallel mechanism based on screw theory.Journal of Yanshan University, 2014, 38(1): 22-28.(
 0)
0)[17]Zhang Fan, Zhang Dan. Structural synthesis of decoupled spherical parallel mechanism based on driven-chain principle.Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(11): 195-199.(
 0)
0)[18]Zhang Yanbin, Wu Xin. Structural synthesis of fully-decoupled two-translational and two-rotational parallel mechanisms.Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(8): 250-255.(
 0)
0)[19]Ball R A. Treatise on the Theory of Screws.Cambridge: Cambridge University Press, 1900.(
 0)
0)[20]Carricato M, Parenti-Castelli V. Singularity-free fully-isotropic translational parallel mechanisms.The International Journal of Robotics Research, 2002, 21(2): 161-174.DOI:10.1177/027836402760475360(
 0)
0)[21]Zeng Daxin, Hou Yulei, Lu Wenjuan. Type synthesis method for the translational decoupled parallel mechanism based on screw theory.Journal of Harbin Institute of Technology, 2014, 21(1): 84-91.(
 0)
0)[22]Gao Feng, Yang Jialun, Ge Qiaode. Type Synthesis of Parallel Mechanisms Based on GF Set:.Beijing: Science Press, 2004.(
 0)
0)