中值面是三维模型几何与拓扑的一种重要描述子,在模型压缩与近似、动画与形变、检索与识别等方面都有广泛应用前景。但是中值面对噪声的不稳定性使得对其进行化简十分必要。已有的简化方法具有各种各样的缺陷,或者简化质量不高,或者无法保持拓扑,或者依赖于耗时的拓扑检查步骤来保持拓扑(如图1)。
团队观察到边折叠简化中值面过程中拓扑改变的原因,并基于此提出了一个简单易行的拓扑检查策略,能在简化过程中有效规避拓扑改变。同时,由于边折叠操作的局部性质,团队证明了只有在模型孔洞周围才有需要进行拓扑检查。因此,如图2,团队基于投影提取出模型孔洞周围的关键区域,并将拓扑检查限制在关键区域上,避免了大量不必要的计算。此外,为了进一步减小拓扑检查对算法效率的拖累,团队提出了一个有效的并行边折叠简化框架。新方法继承了边折叠简化几何近似质量高的优点,同时还能保持拓扑,且具有较高的计算效率。
该研究不仅在三维模型的中值面简化上具有重要意义,而且为中值面的进一步广泛应用提供了基础。相关工作得到了国家自然科学基金项目的资助。
论文链接:Topology Preserving Simplification of Medial Axes in 3D Models
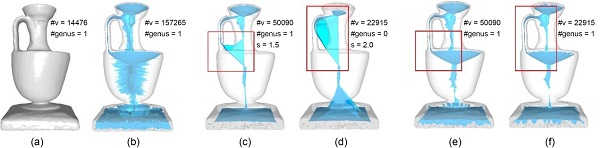
图1:中值面简化和已有方法的对比。(a) 原始模型。(b)初始中值面。(c)-(d)不同参数s的Scale Axis Transform方法化简中值面。
(e)-(f)我们方法化简的中值面。#v表示顶点数,#genus表示亏格。
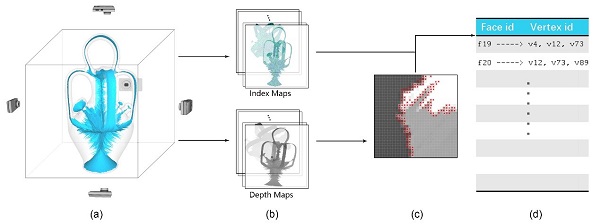
图2:基于投影提取孔洞周围的关键区域。(a)-(b)向6个角度投影得到深度图。(b)-(c)检测深度变化大的像素,作为孔洞边界。
(c)-(d)标记对应三维点为孔洞周围关键区域。
