 , 张德英1,2,3, 施润和1,2,3,4
, 张德英1,2,3, 施润和1,2,3,4

1. 华东师范大学地理科学学院, 上海 200241;
2. 华东师范大学地理信息科学教育部重点实验室, 上海 200241;
3. 华东师范大学环境遥感与数据同化联合实验室, 上海 200241;
4. 华东师范大学科罗拉多州立大学中美新能源与环境联合研究院, 上海 200062
收稿日期: 2018-07-27; 修回日期: 2018-10-13; 录用日期: 2018-10-13
基金项目: 国家重点研发计划项目(No.2016YFC1302602);上海市卫计委重点学科建设项目(No.15GWZK0201);中央高校基本科研业务费项目
作者简介: 周云云(1995—), 女, E-mail:zzzhouyunyun@163.com
通讯作者(责任作者): 施润和, E-mail:shirunhe@163.com
摘要: 利用卫星遥感反演气溶胶光学厚度(AOD)已成为获取宏观、连续空气污染信息的一种有效手段.通过构建AOD-PM2.5的关联模型是实现空间范围内PM2.5监测的主要方法,而气象要素是该模型中的重要输入参数,直接影响到模型模拟的精度.当前诸多模型多采用地面气象要素,缺乏对于不同高度气象要素及其变化对构建AOD-PM2.5关联模型的影响研究.本文以淮河流域五省为例,在实测地面气象资料的基础上,利用再分析气象资料,考虑了从地面至高空不同高度处的气象要素及其垂直变化,运用多元逐步回归方法,对比了地面与不同高度气象要素及其变化量对AOD-PM2.5关联模型的贡献程度.结果表明:①AOD-PM2.5关联模型在不同站点、不同季节的差异仍较为明显,不同高度及随高度变化的气象要素对提高春季AOD-PM2.5关联模型的精度有较显著影响;②考虑了不同高度气象要素及垂直变化的多元逐步回归线性模型的表现优于仅考虑地面气象要素的模型,尤其是春季的改善较明显,RMSE降幅达到近43%;③基于地理加权回归方法的AOD-PM2.5关联模型的估算结果略优于多元逐步回归线性模型.
关键词:淮河流域大气污染PM2.5气象要素气溶胶光学厚度(AOD)
Influence of multiple meteorological parameters and their variations on the association model of AOD and PM2.5
ZHOU Yunyun1,2,3
 , ZHANG Deying1,2,3, SHI Runhe1,2,3,4
, ZHANG Deying1,2,3, SHI Runhe1,2,3,4

1. School of Geographic Sciences, East China Normal University, Shanghai 200241;
2. Key Laboratory of Geographic Information Science, Ministry of Education, East China Normal University, Shanghai 200241;
3. Joint Laboratory for Environmental Remote Sensing and Data Assimilation, East China Normal University, Shanghai 200241;
4. Joint Institute of New Energy and the Environment, East China Normal University and Colorado State University, Shanghai 200062
Received 27 July 2018; received in revised from 13 October 2018; accepted 13 October 2018
Abstract: The use of aerosol optical depth (AOD) data derived from the satellite remote sensing retrievals has become an effective means to obtain large-scale and continuous air pollution information. By combining with particulate matters (PM2.5) observations, various AOD-PM2.5 regression models have been established and become an important method to monitor the changes of PM2.5 concentrations over a wider space. In these models, specific meteorological elements are required as important input parameters, which directly affect the model accuracy. However, most current AOD-PM2.5 models only incorporate surface meteorological elements, and the impact of meteorological parameters at other different heights and their vertical changes are generally missed. Therefore, this study uses the multivariate stepwise linear regression method to construct AOD-PM2.5 models in different sites over the Huaihe River Basin on the basis of surface observations and reanalysis data, with a focus on comparing the contributions of various meteorological parameters at different heights as well as their vertical changes to the model. The main results are as follows: ①the AOD-PM2.5 regression model exhibit significant differences at different sites and seasons. In particular, the incorporation of meteorological parameters at different heights and their vertical variations can greatly improve the AOD-PM2.5 model accuracy in spring. ②The AOD-PM2.5 regression model by including key meteorological parameters at various heights as well as their vertical changes shows superiority over the models only considering the surface meteorological parameters, especially in spring with the root mean square errors reduced by more than 43%. ③The estimation of PM2.5 concentrations from the geographically weighted regression model is slightly better than that from multivariate stepwise linear regression model.
Keywords: Huaihe River Basinair pollutionPM2.5meteorological parametersAOD
1 引言(Introduction)随着我国城市化、工业化的不断发展, 能源消耗、工业污染排放、机动车保有量不断增加, 大气污染问题日趋严重, 空气动力学直径小于等于2.5 μm的颗粒物(PM2.5)作为形成霾的重要成分, 成为研究热点(孟晓燕等, 2013;张智胜等, 2013).PM2.5对可见光的消光作用能引起大气能见度降低(Wang et al., 2009), 并对人体健康(Pope et al., 2004;Stieb et al., 2016)及气候变化(潘月鹏等, 2014)造成严重影响.近年来, 我国大力开展PM2.5监测工作, 并于2012年底初步建成PM2.5地基监测网, 它能实现PM2.5浓度的逐小时监测, 目前这项工作还在不断推进完善中.但地基监测站点存在空间分布不均匀, 城市站点多于农村站点, 东部站点多于西部站点, 难以实现对PM2.5的大范围全覆盖监测的问题.卫星遥感具有实时、连续、覆盖面积大等特点, 能在一定程度上弥补地基监测站点的不足.许多研究表明, 气溶胶光学厚度(Aerosol Optical Depth, AOD)与PM2.5之间具有密切的联系(王静等, 2010;林海峰等, 2013;于文金等, 2016), 而AOD能够通过卫星遥感的手段获取, 因此, 通过建立AOD与PM2.5的关联模型来实现PM2.5的大范围连续监测也逐渐成为PM2.5研究的趋势.尤其随着国产遥感卫星的快速发展, 利用国产卫星资料反演AOD(张璐等, 2016), 并开展区域乃至全国范围的PM2.5监测已成为研究的热点之一(孙立娥等, 2016).
与反映整层大气柱光学特性的AOD相比, PM2.5的形成机制较为复杂, 其在空气中的垂直分布与大气稳定度及扩散能力有关(杨素英等, 2010;王静等, 2015;孙兆彬等, 2017), 因此, 国内外许多****在构建AOD-PM2.5关联模型时加入边界层高度、温度、相对湿度、风速等气象因子, 以提高模型的估算精度(Liu et al., 2005;Gupta et al., 2009;徐建辉等, 2015;陈辉等, 2016).由于高低空环流的配置及形势对大气污染物扩散起着关键作用(饶晓琴等, 2008), 而以往的AOD-PM2.5关联模型中多考虑地面气象要素, 将高、中、低空不同高度气象要素及其垂直变化加入AOD-PM2.5关联模型的研究较少.因此, 本文利用欧洲中尺度天气预报中心的再分析气象资料, 运用多元逐步回归和地理加权回归方法构建AOD-PM2.5关联模型, 并考察地面至高空不同高度的气象要素及其垂直变化对构建AOD-PM2.5关联模型的影响.
2 数据与方法(Data and methods)2.1 研究区概况淮河流域是我国七大江河流域之一, 地处中国东部, 介于长江和黄河两流域之间, 其南北气候差异显著, 淮河以北属于暖温带, 以南属于北亚热带.淮河流域跨越江苏、山东、安徽、河南及湖北五省(图 1).一方面, 淮河流域是我国重要的煤炭生产基地和能源基地, 燃煤与PM2.5的产生关系密切, 是重要的大气污染源之一(龚梦洁等, 2015).另一方面, 秸秆燃烧、工业发展等也会带来一定的大气污染问题(靳全峰等, 2017).2010年第六次人口普查结果显示, 淮河流域的平均人口密度超过600人·km-2, 虽不及京津冀等重要城市群, 但仍居我国七大江河流域之首, 大气污染对人群健康构成了严峻威胁.目前与淮河流域有关的大气污染研究多以单个城市为主, 而对整个淮河流域的研究较少(徐春萌等, 2015).综上, 本文选取淮河流域作为研究区.
图 1(Fig. 1)
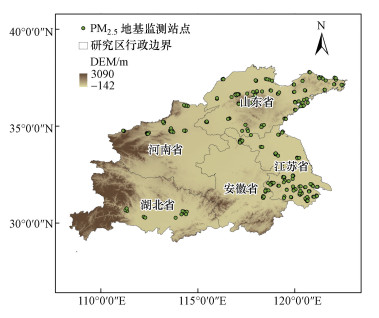 |
| 图 1 淮河流域行政边界及PM2.5地基监测站点分布 Fig. 1Administrative boundary of Huaihe River Basin and distribution of PM2.5 ground monitoring sites |
2.2 数据及预处理2.2.1 地基监测站PM2.5质量浓度数据我国于2012年底初步建成PM2.5地基监测网, 2013年开始发布相关数据.本研究获取了2014年3月—2015年2月淮河流域五省共267个地基监测站点的逐小时PM2.5地基监测站点数据, 研究区内地基监测站点空间分布如图 1所示.
2.2.2 气溶胶光学厚度数据美国NASA(National Aeronautics and Space Administration)通过搭载在TERRA及AQUA卫星的MODIS传感器能基本实现每天上午和下午各覆盖全球一次的观测, 并发布多种大气相关反演参数产品.MODIS气溶胶产品主要监测全球海洋与陆地上空大气气溶胶光学厚度, 可用于建立气溶胶模型、监测大气污染等, 在大气科学领域得到了广泛应用(Ichoku et al., 2004).MODIS C6气溶胶产品于2013年发布, 该产品的精度可达(±0.05±0.20)τa(Remer et al., 2013), 自发布以来, 已在PM2.5及其他研究中广为使用.本研究通过NASA数据发布平台获取淮河流域五省份TERRA/MODIS C6二级瞬时气溶胶光学厚度反演产品MOD04, 并提取0.55 μm波段处的AOD数据.该数据空间分辨率为3 km, 时间分辨率为24 h, 过境时间为地方时10:30左右.
2.2.3 气象数据再分析气象资料具有类型丰富、覆盖范围广等特点, 本研究获取的气象数据来源于欧洲中尺度天气预报中心(ECMWF)的再分析气象资料, 其空间分辨率为0.125°×0.125°, 边界层高度时间分辨率为12 h, 其余气象要素均为逐6 h再分析气象资料, 该再分析气象资料在PM2.5估算研究中使用较为广泛.由于使用的TERRA/MODIS AOD数据在中国的过境时间为10:30左右, 因此, 本研究使用UTC 0时气象数据以尽可能与AOD过境时间匹配.除PM2.5估算研究中常规使用的温度、湿度、风速、风向等地面气象要素外(Liu et al., 2005; Gupta et al., 2009; 于文金等, 2016), 本研究还考察了这些气象要素的垂直分布及变化.在高度上, 为表征不同高度气象数据及其垂直变化, 使用比较具有代表性的几个等压面高度(1000、850、700、500、300及100 hPa)的气象数据.本文具体使用的气象要素如表 1所示.
表 1(Table 1)
| 表 1 气象要素集 Table 1 Meteorological parameters | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 气象要素集 Table 1 Meteorological parameters
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2.4 数据处理为了研究气象要素对AOD-PM2.5关联模型的影响, 将研究获取的基础数据进行时间及空间上的匹配.由于使用的气溶胶光学厚度数据为搭载于Terra卫星上的MODIS AOD产品, 其在中国过境时间为上午10:30左右, 因此, PM2.5取10:00、11:00、12:00的有效平均浓度, 提取PM2.5地基监测站点处的AOD及气象数据, 以日期及站点位置为依据实现PM2.5与AOD及气象数据的时空匹配.在剔除AOD反演无效值后, 最终得到2014年3月—2015年2月本研究区域的有效匹配记录8543条, 其中, 春、夏、秋、冬季分别为3093、1988、2753、709条.
2.3 研究方法2.3.1 多元逐步回归多元逐步回归是在自变量数据大于2个的情况下, 根据自变量对因变量影响的贡献大小逐个引入回归方程, 得到贡献率大的自变量而剔除贡献率小的自变量的过程.本研究考虑的气象要素多达50个, 因此, 在进行多元逐步回归前, 首先利用SPSS软件计算各自变量的相关系数(r), 使用方差膨胀因子(VIF)作为评价指标(Marquardt et al., 1985), 对自变量进行共线性检验, 具体如式(1)所示.
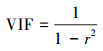 | (1) |
2.3.2 地理加权回归地理加权回归模型由Fortheringham等在1996年提出, 它是多元线性回归模型的一种扩展.与多元线性模型不同的是, 地理加权回归模型考虑局部特征作为权重, 是一种局部空间回归模型, 模型回归系数随地理位置的不同而变化.地理加权回归模型的一般形式为:
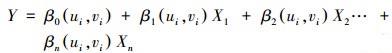 | (2) |
3 结果与分析(Results and analysis)3.1 各季节入选气象要素差异分析多元逐步回归方法能通过计算和比较各自变量对因变量的贡献大小, 选入贡献率最大的若干自变量建立回归方程.本文使用F值的显著性水平作为判定条件:当变量的F值显著性水平小于0.05时选入模型, 若该显著性水平大于0.1, 则剔除变量, 从而得到对AOD-PM2.5估算模型影响显著的气象因子.
由于不同气象要素对PM2.5的影响具有季节性差异, 在相同逐步回归条件下, 各季节入选气象要素数量存在差别.4个季节入选气象要素由多至少依次为(图 2):秋季(15)、春季(14)、冬季(9)、夏季(5个).本研究将气象数据归为3类, 统计各季节3类气象要素入选次数, 总体而言, 随高度变化气象要素入选最多, 共18次, 其次为不同高度气象要素(16次), 地面气象要素(9次)入选次数最少.
图 2(Fig. 2)
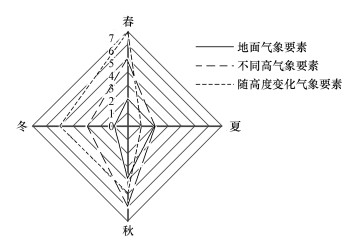 |
| 图 2 各季节3类气象要素入选回归模型的次数统计 Fig. 2Statistics on the number of three kinds of meteorological elements selected into the regression model in each season |
根据3类气象要素在各季节的选入情况(图 3), 统计发现, 温度相关气象要素选入次数最多, 其次为风速及相对湿度.不同高度的温度及其垂直变化能够反映大气垂直稳定性, 尤其是逆温.当近地层存在逆温时, 大气层结稳定, 大气垂直运动减弱, 不利于污染物的扩散, 因而容易造成污染物堆积, PM2.5浓度上升(何永晴等, 2014;孙兆彬等, 2017).风对大气污染物的扩散及输送起重要作用, 风速越大, 越有利于污染物的扩散稀释及输送, 反之, 越不利(杨洋等, 2016).由于本文使用的是不同高度的水平风速(包括经向风速和纬向风速), 并未直接考虑全风速, 因此, 总体入选次数少于温度要素, 且季节差异显著.PM2.5粒径小, 易吸附水汽而涨化变成雾状颗粒, 从而影响其光学特性, 因此, 不同高度相对湿度也是影响AOD-PM2.5关联模型的重要因素之一.
图 3(Fig. 3)
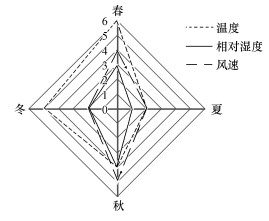 |
| 图 3 各季节温度、相对湿度、风速相关气象要素入选次数 Fig. 3Number of meteorological factors related to temperature, relative humidity and wind speed selected in each season |
各季节除选入气象要素的数量及类型存在差异外, 其在各季节回归模型中的选入顺序也不同, 表 2展示了各季节入选的前5位气象要素.春季最先入选的气象因子为850 hPa与1000 hPa温度差, 表明其对PM2.5的贡献优于地面气象要素, 且前5个气象要素中, 有3个为垂直温度变化, 反映出温度垂直梯度对春季AOD-PM2.5关联模型具有重要作用.夏季优先入选的气象要素为地面经向风速, 但夏季入选气象要素中, 随高度变化温度对PM2.5的贡献优于地面其他气象要素被模型选入, 且入选的前5个气象要素中, 有3个为非地面观测气象要素.秋季选入的气象要素主要集中在近地面和低空850 hPa, 包括了温度、湿度、风速和边界层高度, 体现出该季节的气象因子影响较为复杂.冬季也以不同高度处的温度及其变化要素为主, 在前5个入选气象要素中占了3个.
表 2(Table 2)
| 表 2 各季节按顺序入选的贡献率前5气象要素 Table 2 The top five meteorological parameters were selected in order of each season | ||||||||||||||||||||||||||||||||||
表 2 各季节按顺序入选的贡献率前5气象要素 Table 2 The top five meteorological parameters were selected in order of each season
| ||||||||||||||||||||||||||||||||||
综上可见, 不同高度处的气象要素及其垂直变化, 在建立AOD-PM2.5关联模型中起到重要作用, 且因季节而异.
3.2 气象要素筛选前后对比分析通过随机取样的方式, 使用70%有效匹配数据(春、夏、秋、冬各2165、1392、1927、496条)分别构建仅考虑地面气象要素与考虑表 1所列全部气象要素的分季节AOD-PM2.5关联模型, 用其余的30%有效匹配数据(春、夏、秋、冬各928、596、826、213条)对模型进行验证, 并比较两种模型验证的拟合R2及均方根误差(RMSE, root-mean-square error).表 3展示了考虑全气象要素的多元逐步回归模型, 该模型与仅加入地面气象要素的模型相比表现更好, 尤其春季的改善最明显, R2提高了4%, RMSE降低近43%.夏季和冬季的R2及RMSE均略有改善, 秋季R2提高, 但秋季RMSE略高了0.8 μg·m-3.上述结果表明, 利用AOD进行PM2.5估算时, 除地面气象要素外, 将不同高度气象要素及其垂直变化考虑进去, 能在一定程度上改善AOD-PM2.5关联模型的估算精度.
表 3(Table 3)
| 表 3 各季节多元逐步回归模型及验证结果 Table 3 Multivariate stepwise regression models and validation results for each season | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3 各季节多元逐步回归模型及验证结果 Table 3 Multivariate stepwise regression models and validation results for each season
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3 地理加权回归结果分析由于淮河流域范围较大, 各地下垫面土地利用、人口、工农业生产方式等存在差异, 导致同样的气象要素可能对颗粒物的形成和扩散产生不同影响, 即气象要素在不同地理环境的表现存在差异, 也即回归系数与空间位置相关, 而在整个研究区使用一种AOD-PM2.5关联模型无法反映因地理环境变化导致的各变量局部参数变化(Chu et al., 2006).相关研究表明, 基于地理加权回归(GWR)的PM2.5估算优于多元线性回归模型, 并且更能反映PM2.5的局部特征(陈辉等, 2016).本文运用GWR方法, 使用筛选出的地面和不同高度及随高度变化气象要素, 建立分季节的AOD-PM2.5关联模型.
构建地理加权回归模型时, 使用与3.2节中多元逐步线性回归模型相同的建模数据与验证数据.对4个季节GWR模型结果进行验证, 计算各季节的模型拟合精度及均方根误差(RMSE), 结果如图 4所示, 与加入筛选后气象要素的多元逐步回归模型(表 3)相比, GWR模型的R2在春、夏、秋、冬4个季节分别提高了13%、10%、12%、13%, RMSE分别降低了9.4%、7.4%、21.2%、13.9%.
图 4(Fig. 4)
 |
| 图 4 各季节地理加权回归模型验证拟合结果散点图 (a.春季, b.夏季, c.秋季, d.冬季) Fig. 4Validation fitting results of geographically weighted regression model |
基于上述地理加权回归模型计算2014年3月—2015年2月淮河流域五省份PM2.5空间分布情况, 最后得到该研究时间范围内PM2.5季均浓度的空间分布(图 5).受云覆盖等因素的影响, 有些地方无法获取有效的AOD值, 因此, 淮河流域PM2.5季均浓度仍存在缺值, 但这并不影响对淮河流域PM2.5空间分布特征的整体分析.从图中可以看到, PM2.5的空间分布季节差异显著, 整体而言, 冬季PM2.5浓度最高, 且冬季高值区成片分布, 范围较广, 尤其在湖北、河南及山东省表现得较为明显, 其次为春季, 夏季PM2.5浓度最低;除此之外, PM2.5的空间分布还具有地域性特征, 春季五省PM2.5空间分布差异较小, 夏季江苏、安徽、山东的PM2.5浓度高于河南及湖北, 秋季山东、河南、安徽三省PM2.5浓度高于湖北及江苏两省, 冬季各省的PM2.5浓度整体较高.
图 5(Fig. 5)
 |
| 图 5 各季节PM2.5空间分布 (a.春季, b.夏季, c.秋季, d.冬季) Fig. 5Spatial distribution of PM2.5 concentration in each season |
4 结论(Conclusions)本文以淮河流域为研究区, 利用再分析气象资料中不同高度处的气象要素数据及其垂直变化情况, 结合地面观测气象数据, 通过统计分析, 研究气象要素在AOD-PM2.5关联模型中的作用, 旨在更好地开展区域PM2.5估算.本文研究主要结论如下:
1) 不同高度处的气象要素及其垂直变化对PM2.5估算具有较显著的影响, 这种影响在研究区内具有季节差异, 有必要建立分季节的AOD-PM2.5关联模型.
2) 考虑不同高度处气象要素及其垂直变化所构建的PM2.5多元线性模型精度优于仅考虑地面气象要素的模型, 不同季节的模型精度改善程度略有差异, 春季最为显著, RMSE降低近43%.同时, 不同季节模型的入选参数也有差异, 其中, 不同高度处的温度及其垂直变化是最主要的.可见, 在现有地面观测气象数据的基础上, 增加再分析资料提取的不同高度处气象要素数据及其垂直变化是有必要的.
3) 基于地理加权回归模型的PM2.5估算精度优于多元线性回归模型, 各季节的拟合R2及RMSE均有改善, 其中, 秋季改善最大, R2提高了12%且RMSE降低了21.2%, 反映出气象要素对于AOD-PM2.5关联模型的影响存在明显的空间异质性.
5 建议(Suggestions)综上, 考虑多样气象要素进行筛选并构建地理加权回归模型进行PM2.5估算具有一定的优势, 但依然存在一些不足:
1) 本文使用的TERRA/MODIS AOD为卫星观测的瞬时数据, 且为大气整层AOD, PM2.5为小时平均浓度, 气象数据为UTC 0时再分析气象资料, 目的是让三者在时间上尽量匹配, 但这样依然无法消除时间不完全同步造成的影响.
2) 卫星观测AOD为瞬时数据, 且受天气条件影响, 有效AOD大多为晴空数据, 但进行PM2.5估算时, 仍用其构建模型估算每天的PM2.5浓度, 基于日数据计算月均值与季均值时, 尽管该问题能得到一定的缓解, 但仍存在一定的误差.
3) 尽管气象要素对AOD-PM2.5的影响存在地域性差异, 但本文并未直接将地理地貌特征放入模型, 而是通过将地理位置嵌于模型中来间接体现地域性差异的影响, 在未来的研究中, 可考虑区域范围内不同土地利用类型甚至人口等作为自变量, 研究其对AOD-PM2.5关联模型的影响.
4) 气象条件对AOD-PM2.5的影响机制复杂, 尽管本文选择的气象要素均与PM2.5的吸湿沉降、扩散等过程有关, 但本文未从其影响的物理层面分析, 更多的还是从统计层面出发, 因此, 未来研究可更多地从物理上对影响AOD-PM2.5模型的气象因素进行分析.
参考文献
| 陈辉, 厉青, 张玉环, 等. 2016. 基于地理加权模型的我国冬季PM2.5遥感估算方法研究[J]. 环境科学学报, 2016, 36(6): 2142–2151. |
| Chu D A. 2006.Analysis of the relationship between MODIS aerosol optical depth and PM2.5 in the summertime US[C]. Proc. SPIE 6299, Remote Sensing of Aerosol and Chemical Gases, Model Simulation/Assimilation and Applications to Air Quality. San Diego, California.DOI: 10.1117/12.678841 |
| 龚梦洁, 李惠民, 齐晔. 2015. 煤制天然气发电对中国碳排放和区域环境的影响[J]. 中国人口·资源与环境, 2015, 25(1): 83–89.DOI:10.3969/j.issn.1002-2104.2015.01.012 |
| Guo Y, Tang Q, Gong D Y, et al. 2017. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model[J]. Remote Sensing of Environment, 198: 140–149.DOI:10.1016/j.rse.2017.06.001 |
| Gupta P, Christopher S A. 2009. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products:Multiple regression approach[J]. Journal of Geophysical Research:Atmospheres, 114(D14).DOI:10.1029/2008JD011496 |
| 何永晴, 赵玉成, 冯蜀青. 2014. 西宁市逆温特征及其与空气污染物浓度的相关分析[J]. 冰川冻土, 2014, 36(3): 608–613. |
| Ichoku C, Kaufman Y J, Remer L A, et al. 2004. Global aerosol remote sensing from MODIS[J]. Advances in Space Research, 34(4): 820–827.DOI:10.1016/j.asr.2003.07.071 |
| 靳全锋, 马祥庆, 王文辉, 等. 2017. 华东地区2000—2014年间秸秆燃烧排放PM2.5时空动态变化[J]. 环境科学学报, 2017, 37(2): 460–468. |
| 林海峰, 辛金元, 张文煜, 等. 2013. 北京市近地层颗粒物浓度与气溶胶光学厚度相关性分析研究[J]. 环境科学, 2013, 34(3): 826–834. |
| Liu Y, Sarnat J A, Kilaru V, et al. 2005. Estimating ground-level PM2.5 in the eastern United States using satellite remote sensing[J]. Environmental Science & Technology, 39(9): 3269–3278. |
| Marquardt D, Snee R. 1985. Developing Empirical Models with Multiple Regression:Biased Estimation Techniques[M]. Boulder, Colorado: Westview Press: 45–100. |
| 孟晓艳, 魏桢, 王瑞斌, 等. 2013. 灰霾试点城市PM2.5浓度特征及其影响因素分析[J]. 环境科学与技术, 2013, 36(9): 76–80.DOI:10.3969/j.issn.1003-6504.2013.09.016 |
| 潘月鹏, 贾琳, 田世丽, 等. 2014. 大气霾污染对农业生产的可能影响[J]. 农业环境科学学报, 2014, 33(11): 2279–2280.DOI:10.11654/jaes.2014.11.030 |
| Pope C A, Burnett R T, Thurston G D, et al. 2004. Cardiovascular mortality and long-term exposure to particulate air pollution:epidemiological evidence of general pathophysiological pathways of disease[J]. Circulation, 109(1): 71–77.DOI:10.1161/01.CIR.0000108927.80044.7F |
| 饶晓琴, 李峰, 周宁芳, 等. 2008. 我国中东部一次大范围霾天气的分析[J]. 气象, 2008, 34(6): 89–96. |
| Remer L A, Mattoo S, Levy R C, et al. 2013. MODIS 3 km aerosol product:algorithm and global perspective[J]. Atmospheric Measurement Techniques, 6(1): 69–112.DOI:10.5194/amtd-6-69-2013 |
| Stieb D M, Chen L, Beckerman B S, et al. 2016. Associations of pregnancy outcomes and PM2.5 in a national Canadian study[J]. Environmental Health Perspectives, 124(2): 243.DOI:10.1289/ehp.1408995 |
| 孙立娥, 崔文连, 王艳玲, 等. 2016. 基于环境一号卫星的PM2.5浓度遥感反演研究[J]. 中国环境监测, 2016, 32(3): 129–134. |
| 孙兆彬, 李梓铭, 廖晓农, 等. 2017. 北京大气热力和动力结构对污染物输送和扩散条件的影响[J]. 中国环境科学, 2017, 37(5): 1693–1705.DOI:10.3969/j.issn.1000-6923.2017.05.012 |
| Wang K, Dickinson R E, Liang S. 2009. Clear sky visibility has decreased over land globally from 1973 to 2007[J]. Science, 323(5920): 1468–1470.DOI:10.1126/science.1167549 |
| 王静, 杨复沫, 王鼎益, 等. 2010. 北京市MODIS气溶胶光学厚度和PM2.5质量浓度的特征及其相关性[J]. 中国科学院研究生院学报, 2010, 27(1): 10–16. |
| 王静, 施润和, 李龙, 等. 2015. 上海市一次重雾霾过程的天气特征及成因分析[J]. 环境科学学报, 2015, 35(5): 1537–1546. |
| 徐春萌, 蔡旭晖, 宋宇. 2015. 淮河流域重点城市大气污染源区特征的印痕分析[J]. 北京大学学报(自然科学版), 2015, 51(5): 812–820. |
| 徐建辉, 江洪. 2015. 长江三角洲PM2.5质量浓度遥感估算与时空分布特征[J]. 环境科学, 2015, 36(9): 3119–3127. |
| 于文金, 于步云, 谢涛, 等. 2016. 基于MODIS气溶胶光学厚度与气象要素的苏锡常地区PM2.5地面浓度分布研究[J]. 环境科学学报, 2016, 36(10): 3535–3542. |
| 杨素英, 赵秀勇, 刘宁微. 2010. 北京秋季一次重污染天气过程的成因分析[J]. 气象与环境学报, 2010, 26(5): 13–16.DOI:10.3969/j.issn.1673-503X.2010.05.003 |
| 杨洋, 王红磊, 侯雪伟, 等. 2017. 石家庄一次持续性霾过程形成原因及气溶胶垂直探空分析[J]. 环境科学学报, 2017, 37(3): 824–832. |
| 张璐, 施润和, 李龙. 2016. 基于HJ-1卫星数据反演长江三角洲地区气溶胶光学厚度[J]. 遥感技术与应用, 2016, 31(2): 290–296. |
| 张智胜, 陶俊, 谢绍东, 等. 2013. 成都城区PM2.5季节污染特征及来源解析[J]. 环境科学学报, 2013, 33(11): 2947–2952. |
