作为一种宏观量子物态，超导体具备零电阻和完全抗磁性等独特的物理特性，在医疗、信息、交通、能源、量子科技等众多领域具有重要的应用价值，百余年来受到了学术界和工业界的广泛关注。BCS（Bardeen-Cooper-Schrieffer）超导微观理论指出，超导起源于自旋和动量相反的两个电子结合形成的零质心动量库珀对（Cooper pairs）相干凝聚。然而，当时间反演对称性被破坏时（如施加强磁场），理论上超导体中自旋相反的两个电子可以形成质心动量不为零的库珀对，对应的超导序参量在实空间中呈现出周期性调制（波动）特征，即著名的FFLO（Fulde-Ferrell-Larkin-Ovchinnikov）态。虽然早在1964年FFLO态就被提出，但这一特殊超导态的实现对材料和实验条件有着非常苛刻的要求。直到今天，FFLO态存在的直接证据，譬如实空间中周期性波动的超导序参量，实验上仍然很难获得。

在研究铜基超导体中出现的二维超导特性时，有理论指出非零动量的库珀对有可能出现在保持时间反演对称性的强相互作用系统中，这一新型超导态的库珀对密度在实空间会出现周期性的波动，所以被称为配对密度波（pair density wave，PDW）态。配对密度波这一奇异超导特性与非常规超导，尤其是铜基高温超导之间的关联性引起了理论方面的持续关注和研究。在诸多关于配对密度波的理论中，最引人注目的是配对密度波在铜基高温超导体的相图中可能是一种与d波超导并存的重要主导序，有望提供一个统一的视角来理解高温超导相图中复杂的交织序（intertwined orders），以及这些交织序与高温超导电性的关联。同时，铜基超导体相图中神秘的赝能隙（pseudogap）相，被部分理论工作认为可能来自于配对密度波序。然而前期只在部分铜基高温超导体中观测到了支持配对密度波存在的证据。在铜基超导体之外的第二类高温超导家族——铁基超导体中，配对密度波态一直未得到实验的证实。此外，早期配对密度波理论研究指出，配对密度波是以低维的形式存在于非常规超导体中，遗憾的是，一直未能得到实验的明确验证。
近日，北京大学物理学院量子材料科学中心王健教授课题组与波士顿学院汪自强教授、上海大学张燚副研究员合作，在二维铁基高温超导体Fe(Te,Se)薄膜中发现了本征配对密度波。这一工作是首次在铁基超导体中观测到本征配对密度波，为研究非常规超导体中的配对密度波、非常规高温超导电性以及拓扑电子态提供了一个全新的低维高温超导平台。该工作以《单层铁基高温超导体中的配对密度波态》（“Pair density wave state in a monolayer high-T_c iron-based superconductor”）为题，于2023年6月28日在线发表于学术期刊《自然》（Nature）。中国科学院物理研究所高鸿钧院士与陈辉副研究员在同期《自然》“新闻和观点”（News & Views）栏目中对该工作以及同期发表的其他三篇相关工作进行了评述。
王健课题组利用超高真空分子束外延（MBE）技术在钛酸锶衬底上成功制备出大尺度、高质量的单层铁碲硒【Fe(Te,Se)】高温超导薄膜，其超导能隙高达18 meV，远大于块材铁碲硒（一种重要的拓扑超导候选材料）。在前期的相关研究中，王健课题组在单层Fe(Te,Se)薄膜的一维原子缺陷链两端观测到了稳定存在的零能束缚态，其特征与马约拉纳零能模相吻合【Nat. Phys. 16，536—540（2020）】。在本工作中，王健课题组通过原位低温（4.3 K）扫描隧道显微镜（STM）和扫描隧道谱（STS）技术，对单层Fe(Te,Se)薄膜表面的另一种自发形成的原子级缺陷——晶格沿Fe原子最近邻方向挤压形成的畴界展开了系统研究（图1a—d）。课题组首先测量了畴界处局域态密度的空间分布，观测到了具有实空间周期性调制的局域态密度信号（图1e—f）。利用二维锁相分析技术（图1g—h），课题组确定了这种调制的周期约为3.6a_Fe（a_Fe为最近邻Fe原子之间的距离），并且没有色散，是典型的电荷序引起的空间调制信号。进一步的能量依赖实验表明局域态密度的周期性调制主要存在于超导能隙之中，说明这一电荷序与薄膜的超导态之间存在关联性。

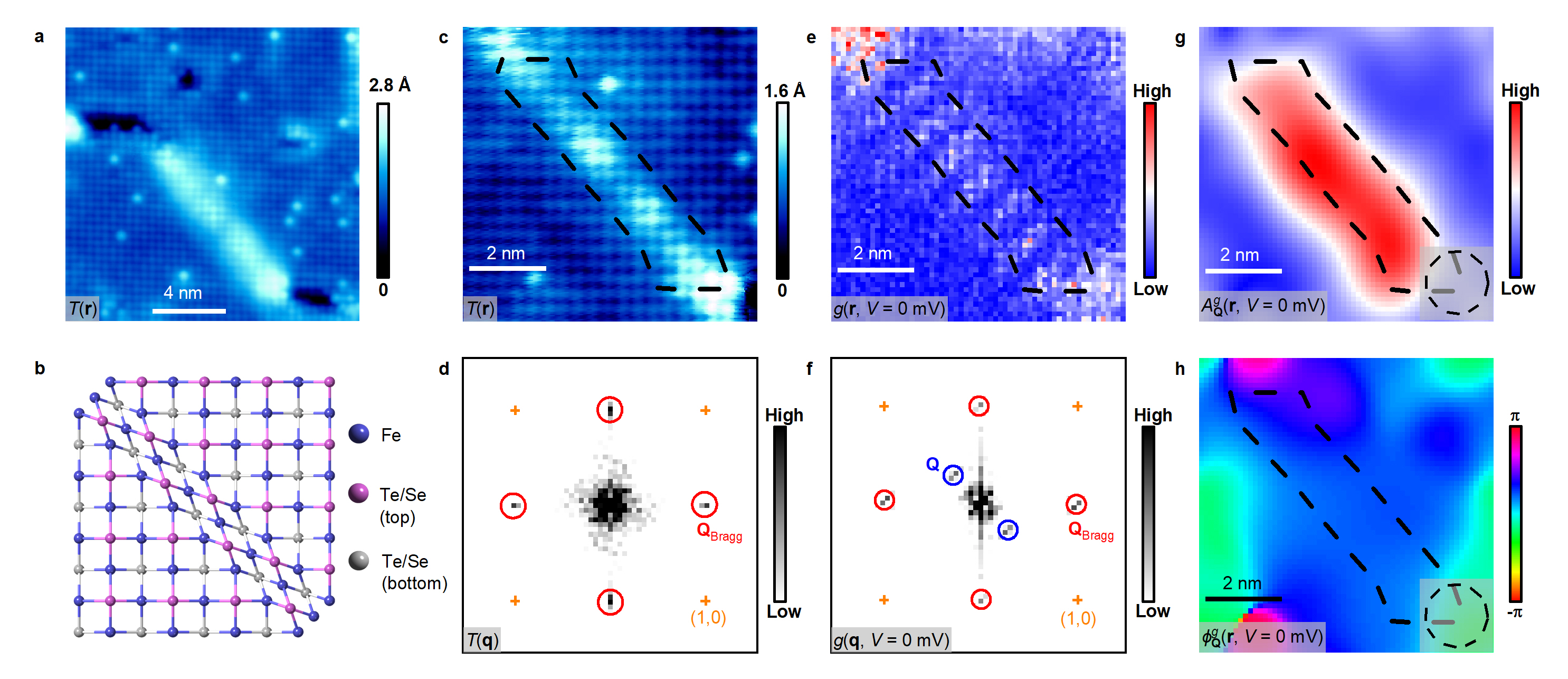
图1 (a) 单层Fe(Te,Se)薄膜的STM形貌图，图中亮线部分为畴界D1所在区域。（b）畴界处晶格结构的模拟示意图，晶格在畴界处沿Fe原子最近邻方向出现挤压。(c)图a中畴界区域放大后的STM形貌图，其中畴界所在区域用黑色虚线标记出。(d)c图的傅里叶变换（FFT）结果，图中只能看到表面Te/Se原子晶格对应的布拉格点（Q_Bragg）。(e) c图所示区域的局域态密度空间分布，在畴界区域内局域态密度表现出周期性的调制结构。(f)e图的FFT结果。除了Q_Bragg外，图中还出现了局域态密度周期性调制对应的波矢Q。(g)局域态密度调制的空间振幅分布，振幅值的大小对应了调制信号的强弱。具有较强调制信号的区域主要集中在虚线所示的畴界范围内。(h)局域态密度调制的空间相位分布，在虚线所示的畴界区域相位较为均匀
课题组进一步对畴界处可能存在的配对密度波展开了系统测量。如图2所示，课题组在畴界处依次观测到了超导相干峰高度（图2a—c）和超导能隙（图2d—g）的空间调制，周期同样为3.6a_Fe。这两个物理量与超导序参量直接相关，从而提供了二维铁基高温超导体中配对密度波的直接实验证据。

图2（a）畴界D2的STM形貌图。（b）沿a图灰色箭头采集的扫描隧道谱，超导相干峰高度调制的周期约为3.6a_Fe。（c）从b图中提取出的超导相干峰高度空间周期调制信号（黑色曲线），红色曲线是经过傅里叶滤波后的周期性调制信号。（d）畴界D3的STM形貌图。（e）d图所示区域的超导能隙空间分布，在畴界区域（黑色虚线）内，超导能隙表现出空间周期性调制特征。插图：超导能隙的统计直方图。（f）沿e图红色箭头提取出的超导能隙信号（红色曲线），表现出周期性调制的特征，经过傅里叶滤波后（蓝色曲线），周期性调制信号变得更为清晰。插图：超导能隙信号（f图中的红色曲线）的FFT结果，其中明显的FFT峰进一步揭示出超导能隙信号的空间周期性调制。（g）e图的FFT结果。在Q~0.28Q_Fe的位置可以看到两个FFT峰，对应实空间周期为3.6a_Fe的超导能隙空间调制。插图：沿(0,0)到(1,0)Q_Fe方向提取的FFT信号（红色曲线），在Q~0.28Q_Fe处出现峰值，与局域态密度调制的波矢一致（黑色曲线）
确认了单层Fe(Te,Se)薄膜畴界处存在配对密度波后，课题组进一步在畴界处得到了周期为1.8a_Fe（配对密度波周期的一半）的电荷密度波存在的证据。通过对配对密度波（周期为3.6a_Fe）和电荷密度波（周期为1.8a_Fe）的空间相位分布进行深入分析，确认了配对密度波空间相位分布中的π-相位变化位置（图3f中箭头所示）与电荷密度波相位分布中的涡旋位置（图3e和3f的黑点所示）存在明显的实空间对应关系。这一对应关系与理论预测的本征配对密度波序（图3a、b）及其诱导出的二阶电荷密度波序（图3c、d）特征一致，证实了所观测到的是本征配对密度波。

图3（a）本征配对密度波序参量示意图。图中黑色圆内为一个半位错（half-dislocation）结构（b）a图对应的相位空间分布，在半位错处表现出π-相位变化。（c）a图中本征配对密度波诱导出的二阶电荷密度波序参量示意图。黑色圆内为配对密度波的半位错结构在二阶电荷密度波中诱导出的拓扑缺陷（topological defect）。（d）c图对应的相位空间分布，在拓扑缺陷处表现出相位卷绕（phase-winding）为2π的涡旋。（e）实验得到的畴界D3附近二阶电荷密度波相位空间分布。黑点处为涡旋的位置。（f）实验得到的畴界D3附近配对密度波相位空间分布。在二阶电荷密度波涡旋（黑点）附近，沿着箭头方向配对密度波出现π-相位变化，与a-d图展示的对应关系一致。插图：沿图中箭头方向的配对密度波相位演化
为了解释畴界处配对密度波的微观机制，汪自强与张燚根据实验结果提出了相同自旋电子配对（equal-spin pairing）模型。由于畴界所在区域的空间反演对称性破缺导致Rashba与Dresselhaus自旋轨道耦合的存在，畴界处相同自旋的电子可以形成非零动量的库珀对，进而产生本征配对密度波。基于该理论模型得到的模拟计算结果与实验数据基本一致，表明畴界处的配对密度波可能具有自旋三重态的拓扑超导特征。
该工作中，王健和汪自强为共同通讯作者，北京大学物理学院量子材料科学中心博雅博士后刘彦昭与博士生魏天恒为共同第一作者，合作者还包括量子材料科学中心博士后何冠阳和上海大学张燚。
该工作得到了国家重点研发计划、国家自然科学基金、量子物质科学协同创新中心、北京市自然科学基金、合肥国家实验室科技创新2030——“量子通信与量子计算机”重大项目、中国科学院卓越创新中心、中国博士后科学基金和美国能源部基础能源科学基金的支持。