在太空物理研究中,一种被称作动理学阿尔芬波(kinetic Alfven waves)的波受到了极大关注。这一波动可以视为跨越宏观的流体尺度(>107千米)的阿尔芬波向微观的离子尺度(>101千米)的拓展。其最为突出的特点是频率接近离子回旋频率,且垂直波长接近离子回旋半径。这些特性使得动理学阿尔芬波能够有效地参与微观的离子尺度的各种动力学过程,介导能量从宏观尺度向微观尺度的传递,并导致能量在微观尺度上的耗散。
动理学阿尔芬波在宇宙等离子体中具有显著作用。长期以来,人们认为它们在行星磁层-电离层-热层耦合中起着重要作用。例如,动理学阿尔芬波可以将大量能量输送到电离层,从而导致极光。此外,这些能量还可以被用于加热和加速电离层中的离子和电子,导致电离层流和大气逃逸。动理学阿尔芬波广泛存在于地球磁层中,并被认为可以显著加速磁层能量粒子并引发地磁活动,对在轨航天器的安全构成威胁。动理学阿尔芬波也被认为是空间和天体等离子体湍流的主要成分之一。
另外,宇宙等离子体还有一个特征,就是构成其的粒子质量相差很大。例如,地球磁层等离子体主要由质子和电子组成,它们的质量相差约1836倍。这种差异导致等离子体波动的时间和空间尺度也相差巨大。例如,在地球磁层中,等离子体波动的频率可从mHz延伸到kHz,跨越了6个数量级。我们可以粗略地将等离子体动力学所涉及的物理尺度从大到小分为三个范围:(1)流体尺度,在这一尺度下,等离子体表现出像连续流体介质一样的特征;(2)离子尺度,在这一尺度下,等离子体中的离子表现出强烈的粒子行为(即需要考虑速度分布函数等微观参数,而不能仅考虑像密度、速度、压强这样的宏观参数),而电子则可以按照连续流体介质处理;(3)电子尺度,这一尺度下,电子和离子都表现出强烈的粒子行为。离子尺度和电子尺度的分界可以用离子在磁场中做回旋运动的频率和半径来表示,而流体尺度和离子尺度的分界可以用电子回旋运动的频率和半径来表示。进一步地,流体尺度可视为宏观尺度,而离子尺度和电子尺度则对应于微观尺度。
不同物理尺度的等离子体波动并不是孤立的,而会发生各种相互作用,并使得能量从宏观尺度传递到微观尺度并耗散为等离子体热能。正是这一过程使得等离子体可以在没有热碰撞参与的情况下发生热弛豫,维持平衡态。研究等离子体波动在等离子体能量跨尺度输运中的作用,以及由此导致的空间和天体等离子体物理过程,是目前空间物理和天体物理研究的前沿热点课题之一。
尽管人们已经认识到动理学阿尔芬波的重要性并因此进行了大量的理论和数值模拟研究,但在利用卫星对其进行实地观测研究方面却进展缓慢。其中的主要困难之一是难以在观测数据中将动理学阿尔芬波和其他等离子体波模区分开。正如前文所述,动理学阿尔芬波的主要特点是其垂直波长接近当地热离子的回旋半径。因此,一个自然而然的识别动理学阿尔芬波的方法即测算观测到的波动的波长,并将其与热离子的回旋半径相比较。但对波长的观测在本质上属于对空间结构的观测,需要对空间中多个位置进行测量。这在实际中是难以做到的,因为除了少数几个特别设计的科学卫星任务(例如Magnetospheric Multiscale和Cluster任务),很难有机会在一个事件中同时有多颗卫星在场。即使有多颗卫星在场,我们也只能测量波长接近卫星间距的波动,否则误差将显著地影响测量结果。为了解决这一问题,也有研究者提出了一些基于单卫星探测的方法。例如,我们可以同时测量等离子体速度分布和磁场,并假设观测到的波动是空间扰动的唯一来源,那么就可以借助安培定律计算波动的波矢,从而得到波长。但这一方法需要对整个等离子体的分布函数进行测量。受制于现有技术限制,这也是难以实现的。
为解决这一问题,在国家自然科学基金项目(批准号:42230202)资助下,北京大学地球与空间科学学院宗秋刚教授带领研究团队最近以“Particle-sounding of the spatial structure of kinetic Alfvén waves”为题在著名学术期刊Nature Communications(《自然·通讯》)发文,提出一种新的测量波动垂直波长的方法,并将其应用于MMS卫星观测到的动力学阿尔芬波事件。该方法利用不同能量的离子具有不同的回旋半径,从而形成了一种测量波动垂直波长的“尺子”。基于这一原理,该方法被称为粒子探测技术(particle-sounding technique)(如图1所示)。

图1. 粒子探测技术示意图(非真实比例)。灰色的细曲线表示磁场线,蓝色背景显示动理学阿尔芬波的相位,底部的红色曲线代表离子的回旋运动轨迹。能量越大,回旋半径越大。动理学阿尔芬波和质子之间的相互作用将显著改变质子的分布函数。这一改变可由MMS航天器进行观测,这一观测结果反过来又提供了一把“尺子”来测量动理学阿尔芬波的垂直波长
更具体地说,波动垂直波长和离子回旋半径之比将显著影响离子和波动之间的相互作用。当离子能量较低时,其回旋半径远小于波动的垂直波长。在这种情况下,离子会与波动电磁场发生显著的相互作用,从而在回旋相位谱上形成与波动波场相关的连续倾斜条纹(见图2第二栏)。随着离子能量的升高,其回旋半径相应地变大。当回旋半径变得与波动垂直波长相当时,离子的运动呈现出一定的混沌性,使得波场对离子的调制作用被“抹平”。换言之,离子不再受到波动的影响。观测中相应的调制信号消失,即回旋相位谱上的条纹断裂(见图2最后两栏)。因此,我们可以通过寻找出现条纹断裂的离子能量,并计算相应的回旋半径,来测量波动的垂直波长。

图2. 2015年12月30日,Magnetospheric Multiscale卫星对一次动理学阿尔芬波-离子相互作用的观测。第一栏展示了波动的垂直电场,后三栏展示了三种不同能量的离子的回旋相位谱;横轴代表时间,纵轴代表回旋相位(即在垂直于背景磁场的平面内,离子速度和某个固定方向的夹角);颜色代表离子的相空间密度,橘色的斜线框出了回旋相位谱上的调制条纹
更进一步地,上述回旋相位谱上的调制条纹断裂信号将首先在和波动运动方向相反的方向上出现。这是因为当离子和波动在垂直于背景磁场的平面内相向运动时,波动和离子之间的相对运动速度最大。根据这一特点,我们可以确定波动垂直传播的方向。
粒子探测技术的可靠性通过和其它测量方法进行对比得到验证。此外,与其它方法的对比还体现出粒子探测技术的优越性。首先,它只需要利用单颗卫星观测;其次,它只需要观测部分能量范围内(常为100 eV~10 keV)的离子分布函数,而不像其它基于单卫星观测方法那样需要对电子和离子的整个分布函数进行测量;最后,它具有较大的量程,可同时测量10~1000 km范围内的垂直波长,覆盖了通常所需的参数空间。
将这一方法初步应用于MMS卫星的探测数据,宗秋刚团队识别出15个动理学阿尔芬波事件,并计算了这些波动的垂直波长。具体分析表明,这些动理学阿尔芬波的垂直波长和基于局地离子温度计算得到的回旋半径具有较好的相关性。如图3所示,前者约为后者的2.4倍。这一结果从观测上证明了动理学阿尔芬波的离子尺度特性,并表明了粒子探测技术对动理学阿尔芬波研究的重要意义。
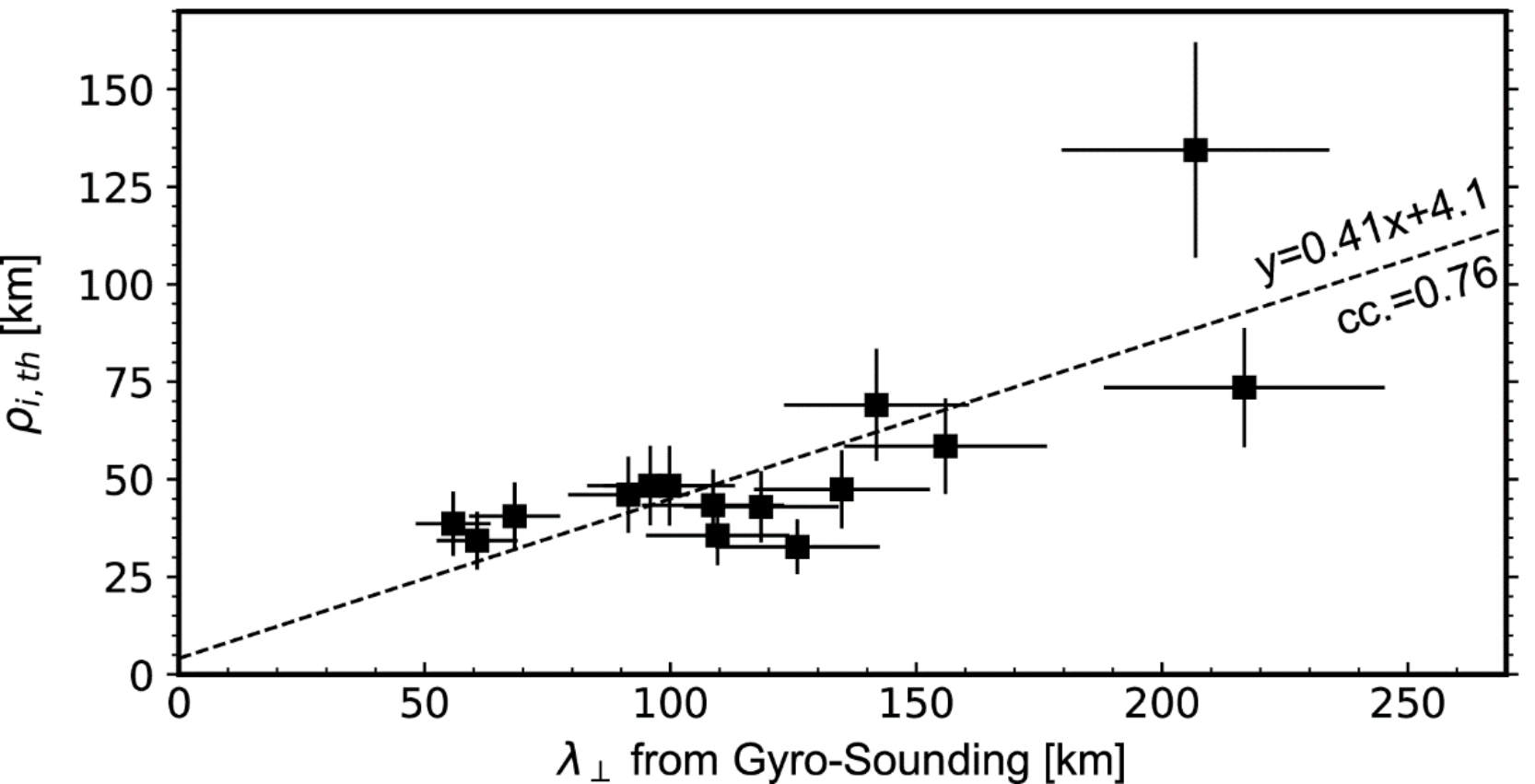
图3. 利用粒子探测技术得到的动理学阿尔芬波垂直波长(横轴)和基于局地离子温度计算得到的离子回旋半径(纵轴)的关系
北京大学地球与空间科学学院空间物理与应用技术研究所博士生刘志扬为文章的第一作者,宗秋刚为通讯作者。这项工作得到国家自然科学基金委的经费和国家重点研发计划“变革性技术关键科学问题”重点专项、民用航天技术预先研究项目的支持。
