Shun Zhan¹, Ru-Fei Cui^2,3, Li-Yan Qiao^,1,3, Jiang-Xing Chen^,1,31Department of Physics, Hangzhou Dianzi University, Hangzhou, 310018, China
²Department of Physics, Zhejiang University, Hangzhou, 310018, China

First author contact: ³Authors to whom any correspondence should be addressed.
Received:2019-08-23Revised:2019-10-18Accepted:2019-10-31Online:2020-01-14

Fund supported:

*Natural Science Foundation of Zhejiang Province.LR17A050001 National Natural Science Foundation of China.11974094 National Natural Science Foundation of China.11674080

Abstract
We propose a new microfluid chip for transporting micro and nano particles. The device consists of chemical stripe pathways full of fuel species, which can be realized in experiments by chemical surface reactions that form spatiotemporal patterns. A mesoscopic model is constructed to simulate the transport dynamics of nanodimers passing through the chip. It is found that the increases of the volume fraction and radius of the dimer both decrease the first reach time although the underlying mechanisms are different: the volume fraction affects the probability of touching and entering the chip while the radius determines the self-propulsion within the chip. The transport efficiency is influenced by the size of the particles.
Keywords： microchip;catalytically sphere dimers;chemical pathway;multiparticle collision dynamics;transport


PDF (615KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Shun Zhan, Ru-Fei Cui, Li-Yan Qiao, Jiang-Xing Chen. Transport of nanodimers through chemical microchip^*. Communications in Theoretical Physics, 2020, 72(1): 015601- doi:10.1088/1572-9494/ab544f

1. Introduction

Catalytically active micro-objects can display self-propulsion through asymmetry reaction when part of their surface catalyses a chemical reaction in a surrounding environment [1–5]. The controlled motion of synthetic nanomotors has attracted considerable interest in fundamental principles and thus stimulated major research efforts over the past decade in connection to diverse potential applications: targeted drug delivery, motion-based biosensing, nanoscale assembly, environmental remediation, etc [6–11].

These small synthetic motors with micro or nano sizes experience very strong thermal fluctuations and operate in regimes where viscous forces dominate [12]. To achieve long-range and directional motion, various external fields have been applied to control their transport. Magnetic fields have been exploited in guiding catalytic nanomotors [13]. However, magnetic control requires the integration of additional magnetic elements in the nanomotors and precise alignment of magnetic moments [14]. Acoustic control has made rapid progress in recent years [15]. For example, it can be utilized in guiding catalytic nanomotors to aggregate and disperse [16], while control of precise motion is still a big challenge. Electric field and light are also applied to control the motion of nanomotors [17, 18].

Without the manipulation by external fields, biological molecular motors, such as kinesins, myosins, and dyneins, use the chemical free energy released by the hydrolysis of adenosine triphosphate ATP as fuel to carry out directed motion along filaments [19]. For synthetic nanomotors, the confined spaces with physical boundary wall, such as capillaries or microchannels and interactions with surfaces, have been applied to assist the directed transport [20–23]. The controlled transport in nanotechnology has been an important topic over the past decade. There are still huge spaces to develop simple but effective lab-on-a-chip devices for transporting micro and nano objects.

In this paper we construct a small chip device consisting of chemical stripe pathways in terms of mesoscopic simulation with hybrid molecular dynamics (MD) and multiple particle collision dynamics (MPC). The chip can transport nanomotors between different containers. The dynamics of dimers passing along the prescribed pathways are studied.

2. Mesoscopic model and simulation method

The device is designed by a container and a microchip including chemical pathways, as shown in figure 1. In the container, nanodimers initially diffuse in the liquid solution which is modeled by amounts of point-like solvent particles (S). The container and the chip are bounded by a wall composed of immobile beads with the radius Σ_b=0.5, except for several entrances. In simulation, the chemical pathways are constructed as follows: when solvent particles (S) diffuse into the stripe pathways they are converted to fuel (F) particles; when molecules diffused out of the pathways they undergo the decay reaction, F (or P)$\mathop{\longrightarrow }\limits^{{k}_{{\rm{cat}}}}{\rm{S}}$, which converts them back to solvent particles with a rate constant k_cat [24]: once the F (or P) diffuse out of the stripe at time t, one can compute the time of the conversion to S at t+t_d from $t+\mathrm{ln}(1/U)/{k}_{{\rm{cat}}}$, where U is a random number chosen from a uniform distribution on the interval [0,1). The self-propelled dimers consist of the catalytic (C) and noncatalytic (N) spheres which are linked by a fixed distance R by a holonomic constraint [25, 26]. The chemical reaction, ${\rm{F}}+{\rm{C}}\to {\rm{P}}+{\rm{C}}$, occurs at the catalytic sphere of the dimer with a subsequent product (P) once a fuel particle (F) touches the surface of the C monomer.

Figure 1.

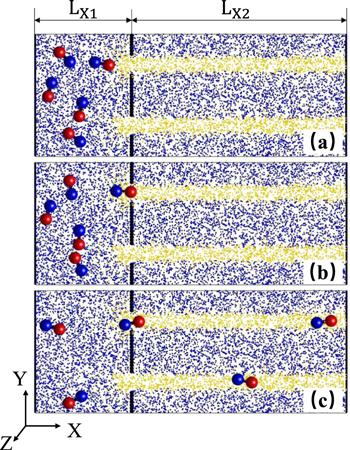
New window|Download| PPT slide
Figure 1.Dynamics of the self-propelled nanodimers in the microfluid chip device. Plots show the instantaneous configuration at (a) t=0, (b) t=850, and (c) t=5600 in a 100×40×5 slice. Five dimers with Catalytic spheres (red) and noncatalytic spheres (blue) are initially placed in the left container full of point-like solvent particles (blue). The chemical pathways are indicated by the stripe full of fuel particles (yellow). The black beads bind the container and the chip. The size parameters: ${L}_{x1}=30,{L}_{x2}=70$ .


The dimers are confined in a three-dimensional slab geometry (${L}_{x}={L}_{x1}+{L}_{x2}=100,{L}_{y}=40,{L}_{z}=20$) between two parallel walls with a distance L_z apart. The dimer motors and Z wall interaction is described through 9-3-Lennard-Jones (LJ) interactions, $V{(r)={\epsilon }_{w}[{({\sigma }_{w}/r)}^{9}-{\sigma }_{w}/r)}^{3}]$, where ϵ_w and Σ_w are the wall energy and distance parameters, respectively. The motors display quasi-two-dimension motion in the x-y plane due to the sphere-wall interactions. The solution contains three types of point-like particles with identical masses m_s, i.e. fuel F, product P, and solvent S particles. Bounce-back boundary condition is applied when these particles collide with the walls in the x and z direction. In the y direction, periodic boundary condition is utilized. The particles in the solution interact with the dimer spheres through repulsive Lennard-Jones interactions, ${V}_{\alpha \beta }{(r)=4{\epsilon }_{\beta }[({\sigma }_{\alpha }/r)}^{12}-{({\sigma }_{\alpha }/r)}^{6}\,+1/4]{\rm{\Theta }}({r}_{c}-r)$, where Θ is a Heaviside function and ${r}_{c}\,={2}^{1/6}{\sigma }_{\alpha }$ is the cutoff distance, with α=C, N and β=F, P, and S, respectively. The interactions of dimer-dimer and dimer-(bead)wall also are also described by the LJ repulsive potential with ϵ_D (${\epsilon }_{\alpha b}$) and Σ_D (${\sigma }_{\alpha b}$).

The simulation of the entire system is carried out by means of a hybrid molecular dynamics (MD) and multiparticle collision (MPC) scheme [27]. In the MD step with time interval t_MD, the motion of each dimer and point-like particles both obey Newton’s equation through calculating total forces on them. No forces among point-like particles in solution are considered. Instead, MPC collision is utilized to simulate the surrounding solution. To carry out collisions, the system is divided into a grid of cells ξ with length a₀. Rotation operators ${\hat{\omega }}_{\xi }(\theta )$ chosen from a set, are assigned to each cell of the system. At the time interval t_MPC after 50 steps of MD motion, particles within each cell collide with each other and the postcollision velocity of particle i in a cell ξ is given by ${{\boldsymbol{v}}}_{i}(t+{t}_{{\rm{MPC}}})={{\boldsymbol{v}}}_{{\rm{cm}}}(t)+{\hat{\omega }}_{\xi }(\theta )({{\boldsymbol{v}}}_{i}(t)-{{\boldsymbol{v}}}_{{\rm{cm}}}(t))$ where v_cm(t) is the center-of-mass velocity of particles in cell ξ. A random shift of the lattice is carried out before the collision step to insure that Galilean invariance is satisfied. This mesoscopic dynamics preserves the essential features of full molecular dynamics.

In the simulation, all quantities reported are in dimensionless units based on energy ϵ_β, mass m_s and distance a₀. The temperature of the system is fixed at k_BT=1.0. Newton’s equations were integrated using the velocity Verlet algorithm with t_MD=0.01. The MPC time is t_MPC=1.0 and the rate constant is k_cat=0.08. The density of point-like particles in solution is n₀=10. The mass of a dimer monomer obeys the relation ${M}_{\alpha }=4{n}_{0}\pi {\sigma }_{\alpha }^{3}/3$ to ensure the dimer is approximately neutrally buoyant. The rotational angle for MPC is fixed at θ=π/2. The LJ potentials parameters are ϵ_w=5.0, ${\sigma }_{w}={L}_{z}/2,{\epsilon }_{F}={\epsilon }_{S}=5.0$, and ${\epsilon }_{P}=0.1$. For interactions between two monomers on different dimers ϵ_D=5.0 and ${\sigma }_{D}=({\sigma }_{\alpha 1}+{\sigma }_{\alpha 2}){2}^{1/6}+0.2$ are used. The interaction parameters between monomers and beads on the bounded wall are ${\sigma }_{\alpha b}=({\sigma }_{\alpha }+{\sigma }_{b}){2}^{1/6}+0.1$ and ${\epsilon }_{\alpha b}=5.0$.

3. Results and discussion

Initially, the dimers display random diffusion in the container since there are no fuel particles in the solution, as seen in figure 1(a). In the vicinity of the exits of the container (i.e. the entrances of the chip), the decay of the fuel F (or P)$\mathop{\longrightarrow }\limits^{{k}_{{\rm{cat}}}}{\rm{S}}$ from the chemical stripes results in a gradient field in the entrance of the pathways. The sharpness of the gradient F field is increased with k_cat. Once the motors move close to the exits that link the chemical stripe pathways on the microchip, they sense the F gradient field and convert the diffusing F particles to P particles on the surface of C monomers. Consequently, the emergence of asymmetric distribution of P particles induces a push force on the dimer to the container exits (note ϵ_P<ϵ_F or (ϵ_S)). Therefore, the chemotactic effect leads to the accelerative approaching of the dimers to the exits. From figure 1(b), one can see one dimer entering into a pathway.

The dimers gradually move into the pathways one by one, as shown in figure 1(c). Since the stripes are full of fuel, the motors can execute self-propulsion along the pathways: the phoretic propulsion drives the dimer with the head of C sphere, which results from the asymmetric distribution of P around the N sphere. Like a micro channel, the chemical route confines the motors within it: once a dimer touches the edge of the stripe pathways, the chemotactic effect will push it back. The confinement from the stripe edge is increased with k_cat. Thus, the dimers undergo long navigation along the route, just like the case where the molecular motors move on the filament network. The microchip constructs a bridge to transport nanoparticles among different containers.

It is well known that chemical patterns ranging from stationary regular and labyrinthine patterns to time-evolving structures can arise in chemical systems driven far from equilibrium. For example, the stripe pattern can be achieved from Turing instability in a Chlorite-iodide-malomic acid (CIMA) system [28]. Another example is the patterns formed by the oxidation of CO on the platinum surface [29]. Therefore, the chemical microfluid chip can be realized in experiments. Also, it is expected that similar chips can be constructed by topographical pathways [22] or chemically patterned surfaces [21].

The self-propulsion of dimer nanomotor along the strip is described by the migration velocity of its center of mass along the x axis, denoted by V_cmx. In the simulation, V_cmx can be changed by tuning the potential difference ${\rm{\Delta }}\epsilon ={\epsilon }_{S}-{\epsilon }_{P}$. The motors fluctuate and move within the path. We define the mean square deviation ΔS to show the position fluctuation in figure 2(a). Since the N sphere is free to rotate due to its lack of catalytic activity, compared to the case of C sphere, the fluctuation is more obvious with a bigger ΔS in figure 2(a). When the self-propulsion becomes stronger with increased V_cmx, the deviation ΔS of C sphere decreases slightly, which indicates that the confinement of C sphere is increased. As for the N sphere, since the dimer is guided by the ‘leader’, the increased velocity of C sphere suppresses the rotational fluctuation of N sphere. Consequently, one can see that ΔS of N sphere decreases distinctively in figure 2(a). The suppression of fluctuation by strong self-propulsion is also confirmed by the averaged angle θ_x. In figure 2(b), θ_x is decreased when V_cmx is increased, which means the rotation fluctuation is weakened, namely, the dimer tends to align along the pathways.

Figure 2.

New window|Download| PPT slide
Figure 2.The dependence of the mean square deviation ΔS and the average angle θ_x on the migration velocity V_cmx. ΔS is defined by ${\rm{\Delta }}S=\sqrt{\langle {(y(t)-{y}_{S})}^{2}\rangle }$ where y(t) and y_S are the y component of the position of dimer sphere and the center position of the strips, respectively. θ_x is defined by $\langle \theta \rangle =\langle \arccos (\hat{{\boldsymbol{u}}}(t)\cdot \hat{{\boldsymbol{x}}})\rangle $ where $\hat{{\boldsymbol{u}}}$ is the unit vector pointing from the N to C motor spheres and $\hat{{\bf{x}}}$ the unit vector of x. The data is obtained from time and ensemble averages over 20 realizations of the dynamics .


When the width of the path is small, the shortage of the fuel particles leads to slow transport of the dimers. The transport velocity increases with the path width, since more fuel particles will be available. However, when the width of the path is larger than the size of a dimer, increasing the width will gradually induce the decrease of the transport velocity. This is because the dimers are released from the confinement of strips, which results in increased fluctuation when they transport within the path.

The first navigation time T_F characterizes the transport dynamics of dimers in the microchip. The value of T_F is calculated by recording the time difference between the initial time and the moment when the first dimer touches the right boundary (x=L_x). Due to the chemotactic effect in the entrance of the chip, the nanodimers can rapidly enter into the path and pass through it with small T_F. Since the motion of the dimers is quasi-two-dimension, we use the area fraction ($\phi =2{N}_{d}\pi {\sigma }_{\alpha }^{2}/{L}_{x1}\times {L}_{y}$) to describe the volume exclusion effect. φ is increased with the number of the dimer, which results in the crowded environment. Although the diffusion of the dimer is decreased in a crowded environment, the enhanced volume exclusion effect results in a higher probability to reach the entrance of the chip. Consequently, the values of T_F are decreased, as the circles shown in figure 3. The decrease is obvious, especially when the φ is small. For example, simulation shows that the T_F with 25 dimers is about half of that with 5 dimers.

Figure 3.

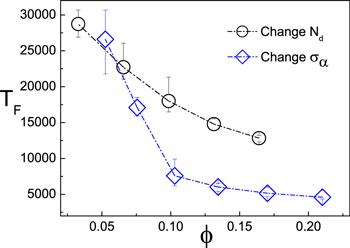
New window|Download| PPT slide
Figure 3.The dependence of the first navigation time T_F on the area fraction φ. The circles are obtained by increasing the number of the dimer monomer (Σ_α=1.0 is fixed, N_d is increased from 5 to 25), while the diamonds are plotted by changing the radius of the dimers (N_d=8). The data is plotted from 20 realizations.


Then, we change the value of φ by fixing the number of the dimers while changing their radius. The size of the dimer increases with φ. Again, the values of T_F decrease as φ is increased. Comparing the two cases in figure 3, one can find that the values of T_F are smaller in the latter case. This is because a bigger dimer has stronger self-propulsion [30], which makes it easier to sense the F particles in the vicinity of the exits and, therefore, move faster within the fuel path.

To study the influences of Σ_α and φ on the T_F further, we fix φ while changing N_d and Σ_α. In figure 4 where φ=0.13 is kept, it is found that T_F increases with Σ_α even when N_d is decreased. This means it is the strong self-propulsion that plays the major role on the T_F. Therefore, one can conclude that Σ_α and φ affect T_F in different ways: increase of φ enhances the probability of entering the pathways entrance while increase of Σ_α enhance the velocity of navigation in the chemical pathways.

Figure 4.

New window|Download| PPT slide
Figure 4.The first navigation time T_F (diamonds) and the transported percentage of dimers R_P (circles) influenced by the radius (Σ_α) and the number (N_d) of the dimers. R_P is obtained by calculating the percent of the dimers that have reached the x=Lx wall at t=50000. The area fraction φ is kept to be 0.13. Σ_α is increased from 1.0 to 2.0 and N_d is decreased from 20 to 5. The data is plotted from 20 realizations.


The transport efficiency of the microchip can be described by the transported percentage of dimers R_P. After long time evolution, we count the percentage of dimers that have reached the right wall as the value of R_P. It is found that R_P increases with φ in figure 5(a). One can see that most of the dimers have reached the wall at t=50000 (R_P=0.88). When φ is fixed while Σ_α is increased in figure 4 (circles), it is shown that the R_P still increases. Simulation indicates the phenomenon is attributed to the stronger self-propulsion of bigger dimers that move rapidly.

Figure 5.

New window|Download| PPT slide
Figure 5.(a) R_P versus φ. N_d=8 is fixed while the Σ_α is changed. (b) The averaged reach time T_r versus φ. T_r is calculated through recoding the reach time of every dimer and averaging them. The data is plotted from 20 realizations.


The dependence of the averaged reach time T_r confirms that the transport efficiency is determined by the power of the self-propulsion. In figure 5(b), one can find T_r is decreased with φ. This means the dimers can reach the right wall within a shorter time. Note that an obvious way to increase the transport efficiency is to increase the number of pathways so that the dimers have more available entrances to the chip, which makes it spend less time to enter into the paths. This point has been observed in simulation.

4. Conclusion

In conclusion, we have chiefly put forward a new design of a microfluid chip for transporting small particles. A particle-based model is set to simulate the dynamics. The first navigating time and transport efficiency are studied by changing the size and the volume fraction of the dimers. The increase of φ and Σ_α both lead to the decrease of T_F while their underlying mechanisms are different. The transport efficiency is also increased with the size of the dimer.

Nanomotors and micromotors need to be able to navigate microfluidic channels to realize their full potential. The transport of nanoscale objects within microfliudic channels represents a significant step toward designing integrated microdevices. The stripe pattern presented here can be realized in chemical reaction, which provides a micro channel without traditional physical boundary. Further studies on experiments can construct more complex pathway networks to perform special tasks. We hope this study may contribute to develop new design of microfluid device.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]PaxtonW FKistlerK COlmedaC CSenAAngeloS KSt.CaoYMalloukT ELammertP ECrespiV H2004 J. Am. Chem. Soc. 126 13424
DOI:10.1021/ja047697z [Cited within: 1]

[2]WangWDuanWAhmedSSenAMalloukT E2015 Acc. Chem. Res. 48 19381946
DOI:10.1021/acs.accounts.5b00025

[3]GolestanianRLiverpoolT BAjdariA2005 Phys. Rev. Lett. 94 220801
DOI:10.1103/PhysRevLett.94.220801

[4]LiangHLiYChenJ XXuJ R2019 Int. J Heat Mass Tran. 130 1189
DOI:10.1016/j.ijheatmasstransfer.2018.09.050

[5]YangM CWysockiARipollM2014 Soft Matter 10 6208
DOI:10.1039/C4SM00621F [Cited within: 1]

[6]WuJBalasubramanianSKaganDManeshK MCampuzanoSWangJ2010 Nat. Commun. 1 36
DOI:10.1038/ncomms1035 [Cited within: 1]

[7]MaXHahnKSanchezS2015 J. Am. Chem. Soc. 137 4976
DOI:10.1021/jacs.5b02700

[8]GuixMOrozcoJGarcíaMGaoWSattayasamitsathitSMerkoçiAEscarpaAWangJ2012 ACS Nano 6 44454451
DOI:10.1021/nn301175b

[9]XuL LMouF ZGongH TLuoMGuanJ G2017 Soc. Rev. 46 69056926
DOI:10.1039/C7CS00516D

[10]PanDMouF ZLiX FDengZ YSunJXuL LGuanJ G2016 J. Mater. Chem. A 4 1176811774
DOI:10.1039/C6TA04010A

[11]XuanM JShaoJ SGaoC YWangWDaiL RHeQ2018 Angew. Chem. Int. Ed. 57 1246312467
DOI:10.1002/anie.201806759 [Cited within: 1]

[12]LeeTAlarcón-CorreaMMikschCHahnKGibbsJ GFischerP2014 Nano Lett. 14 24072412
DOI:10.1021/nl500068n [Cited within: 1]

[13]GhoshAFischerP2009 Nano Lett. 9 2243
DOI:10.1021/nl900186w [Cited within: 1]

[14]BarabanLMakarovDStreubelRMonchIGrimmDSanchezSSchmidtO G2012 ACS Nano 6 3383
DOI:10.1021/nn300413p [Cited within: 1]

[15]RenLWangWMalloukT E2018 Acc. Chem. Res. 51 19481956
DOI:10.1021/acs.accounts.8b00248 [Cited within: 1]

[16]JagajjananiR KLiFMengLZhengHCaiFWangW2015 Small 11 28361846
DOI:10.1002/smll.201403621 [Cited within: 1]

[17]SolovevASmithE JBofBufonC CSanchezSSchmidtO G2012 Angew. Chem. Int. Ed. 50 1087510878
DOI:10.1002/anie.201102096 [Cited within: 1]

[18]YoshizumiYHoneggerTBertonKSuzukiHPeyradeD2015 Small 11 5629
DOI:10.1002/smll.201570255 [Cited within: 1]

[19]CarterN JCrossR A2005 Nature 435 308312
DOI:10.1038/nature03528 [Cited within: 1]

[20]BarabanLHarazimS MSanchezSSchmidtO G2013 Angew. Chem. Int. Ed. 52 5552
DOI:10.1002/anie.201301460 [Cited within: 1]

[21]UspalW EPopecuM NDietrichSTasinkevychM2016 Phys. Rev. Lett. 117 048002
DOI:10.1103/PhysRevLett.117.048002 [Cited within: 1]

[22]SimmchenJKaturiJUspalW EPopescuM NTasinkevychMSánchezS2016 Nat. Commun. 7 10598
DOI:10.1038/ncomms10598 [Cited within: 1]

[23]DeprezLdeBuylP2017 Soft Matter 13 35323543
DOI:10.1039/C7SM00123A [Cited within: 1]

[24]ChenJ XChenY GKapralR2018 Adv. Sci. 5 1800028
DOI:10.1002/advs.201800028 [Cited within: 1]

[25]RobertsonBHuangM JChenJ XKapralR2018 Acc. Chem. Res. 51 23552364
DOI:10.1021/acs.accounts.8b00239 [Cited within: 1]

[26]RuecknerGKapralR2007 Phys. Rev. Lett. 98 150603
DOI:10.1103/PhysRevLett.98.150603 [Cited within: 1]

[27]KapralR2008 Adv. Chem. Phys. 140 89146
DOI:10.1002/9780470371572.ch2 [Cited within: 1]

[28]De KepperPDulosE1997 Pour La Science 235 34
[Cited within: 1]

[29]NettesheimSvon OertzenARotermundH HErtlG1993 J. Chem. Phys. 98 9977
DOI:10.1063/1.464323 [Cited within: 1]

[30]TaoY GKapralR2008 J. Chem. Phys. 128 164518
DOI:10.1063/1.2908078 [Cited within: 1]