Multiple-Photon-Added and -Subtracted Two-Mode Binomial States:Nonclassicality and Entanglement

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

Kai-Cai Li¹^,², Xiang-Guo Meng³, Ji-Suo Wang^,¹^,^?1

Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,College of Physics and Engineering, Qufu Normal University, Qufu 273165, China;

School of Physics and Electronic Engineering, Linyi University, Linyi 276000, China;

Shandong Provincial Key Laboratory of Optical Communication Science and Technology,School of Physical Science and Information Engineering, Liaocheng University, Liaocheng 252059, China

Corresponding authors: ?E-mail:jswang@qfnu.edu.cn

Received:2019-04-8Online:2019-07-1

Fund supported:

*Supported by the National Natural Science Foundation of China under Grant.No. 11347026
the Natural Science Foundation of Shandong Province under Grant.Nos. ZR2016AM03
the Natural Science Foundation of Shandong Province under Grant.No. ZR2017MA011

Abstract
We theoretically analyze the nonclassicality and entanglement of two new non-Gaussian entangled states generated by applying multiple-photon addition and subtraction to a two-mode binomial state. The nonclassical properties are investigated in terms of the partial negativity of the Wigner functions, whose results show that their nonclassicality can be enhanced via one-mode even-number photon operations and two-mode symmetrical operations for the initial two-mode binomial state. We also find that there exists some enhancement in the entanglement properties in certain parameter ranges via one-mode photon-addition and two-mode symmetrical operations.
Keywords： two-mode binomial state;photon addition and subtraction;nonclassicality;entanglement

PDF (1885KB)Metadata Metrics Related articlesExportEndNote|Ris|Bibtex Favorite
Cite this article
Kai-Cai Li, Xiang-Guo Meng, Ji-Suo Wang. Multiple-Photon-Added and -Subtracted Two-Mode Binomial States:Nonclassicality and Entanglement ^*. [J], 2019, 71(7): 807-812 doi:10.1088/0253-6102/71/7/807

1 Introduction

Non-Gaussian entangled states as a new information resource have been drawn much attention, which are mainly because that such states are indispensable for completing a number of tasks of quantum information processing, such as quantum teleportation,^[1] quantum key distribution,^[2] and quantum metrology,^[3] and can be further distilled to generate higher-quality quantum entanglement,^[4-6] which can be useful in improving the quality of some certain real quantum information tasks.

Recently, photon addition, photon subtraction and their coherent superpositions as the typical non-Gaussian operations are usually used to produce non-Gaussian entangled states with highly nonclassical properties. For examples, subtracting or adding photon operations on traditional Gaussian states including two-mode squeezed vacuum thermal states are widely studied from both experimental and theoretical aspects.^[7-14] The achieved results presented how do these non-Gaussian operations affect the entanglement, nonlocality and teleportation fidelity in various degree, and the relationship between them. For a review of quantum state engineering with these non-Gaussian operations, we refer to Refs. [15--16] and references therein.

In this paper we shall introduce the multiple-photon-added and -subtracted two-mode binomial states by repeatedly adding or subtracting photons to or from a two-mode binomial state (TMBS), and theoretically investigate the influences of the photon-addition and -sub-traction on the photon number distributions (PNDs), Wigner functions (WFs), and entanglement of these states.

2 Multiple-Photon-Added and -Subtracted TMBSs

Theoretically, using the Schwinger bosonic realization of the operators, i.e., $J_{+}=a^{\dagger}b$, $J_{-}=ab^{\dagger}$, and $J_{z}=({1}/{2})(a^{\dagger} a-b^{\dagger}b)$, the exponential operator $\mathfrak{R}=\exp (\xi J_{+}-\xi^{\ast}J_{-})$ has the following decomposed form,^[17-18] i.e.,

(1)$$ \mathfrak{R}=\exp ( \zeta J_{+}) \exp [ J_{z}\ln ( 1+\left \vert \zeta \right \vert ^{2}) ] \exp ( -\zeta^{\ast }J_{-})\,, $$

which can result in quantum entanglement by rotating two input states via the unitary transformations

(2)$$ \mathfrak{R}a^{\dagger}\mathfrak{R}^{-1} =a^{\dagger}\cos \frac{\theta}{2}% -b^{\dagger}\e^{\text{i}\phi}\sin \frac{\theta}{2}\,,\\ &\mathfrak{R}b^{\dagger}\mathfrak{R}^{-1} =b^{\dagger}\cos \frac{\theta}{2}% +a^{\dagger}\e^{-\text{i}\phi}\sin \frac{\theta}{2}\,, $$

where $\xi=({\theta}/{2})e^{{-i}\phi}$ and $\zeta=e^{{-i}\phi }\tan ({\theta}/{2})$, $a$ and $b$ are two mode annihilation operators, $[a,a^{\dagger}]=[b,b^{\dagger}]=1$. Indeed, the operator $R$ can also be named beamsplitter operator since it can describe the mechanism of an optical beamsplitter. Based on the beamsplitter operator $R$, an output state is linked to the input state by $\vert {\rm out} \rangle =R\vert {\rm in} \rangle$ in the Schr?dinger picture. Hence, letting a single-mode photon number state $\vert q \rangle$ and another mode vacuum state $\vert 0\rangle $ respectively enter the two input ports of a beamsplitter described by the operator $R$ and get overlapped, thus the final output state is^[19]

(3)$$ \vert \xi \rangle _{q}\equiv \mathfrak{R}\vert 0,q \rangle =\sum_{l=0}^{q}c_{q} \vert l,q-l \rangle\,, $$

with $c_{q}=( {q!}/[{l!(q-l)!(1+|\zeta|^{2})^{q}}])^{1/2} \zeta^{l}$. Thus, Eq. (3) is a TMBS with quantum entanglement since another output has the collapsed state $ \vert q-n \rangle $ when one measures the number state $ \vert n \rangle $ at one output port. Using the normal ordering product of the vacuum projection operator, i.e., $ \vert 0,0 \rangle \langle 0,0\vert =\colon e^{-a^{\dagger}a-b^{\dagger}b}\colon$ ($\colon \colon$ refers to normal ordering) and the technique of integration within an ordered product (IWOP) of operators,^[20-22] we prove that the set of the states $ \vert \xi \rangle _{q}$ can form the completeness relation in the whole Fock space.

Further, performing the multiple-photon-added and -subtracted operations $a^{\dagger m}b^{n}$ and $a^{m}b^{\dagger n}$ on the TMBS, we obtain the normalized output states as

(4)$$ \vert \xi \rangle_{s,a} =a^{\dagger m}b^{n} \vert \xi \rangle _{q}=\mathcal{C}^{-1/2}\sum_{l=0}^{q-n}c_{s,a} \vert l+m,q-l-n \rangle \,, \vert \xi \rangle_{a,s} =a^{m}b^{\dagger n} \vert \xi \rangle_{q}=\mathcal{D}^{-1/2}\sum_{l=m}^{q}c_{a,s} \vert l-m,q-l+n \rangle \,, $$

where $c_{s,a}$ and $c_{a,s}$ are respectively given by

(5)$$ c_{s,a} =\frac{\zeta^{l}}{(1+\vert \zeta \vert ^{2})^{q/2}}% \sqrt{\frac{q!(l+m)!}{(l!)^{2}(q-l-n)!}}\,, c_{a,s} =\frac{\zeta^{l}}{(1+\vert \zeta \vert ^{2})^{q/2}}% \sqrt{\frac{q!(q-l+n)!}{[(q-l)!]^{2}(l-m)!}}\,, $$

and $\mathcal{C},\mathcal{D}$ are the normalization factors, i.e., $\mathcal{C=}\sum_{l=0}^{q-n} \vert c_{s,a} \vert^{2}$, $\mathcal{D=}\sum_{l=m}^{q} \vert c_{a,s} \vert^{2}$. Obviously, when $m=n=0$, namely, no photon addition and subtraction case, both the states $\vert \xi \rangle _{s,a}$ and $ \vert \xi \rangle_{a,s}$ reduce to the TMBS. Besides, the condition $m=n$ corresponds to the symmetrical non-Gaussian operation, while $m\neq n$ refers to the asymmetrical case. Note that photon addition and subtraction operations can be realized by using the parametric downconverter and high transmittance optical beamsplitter under experimentally realistic conditions,^[23-25] hence we confirm that, in physical realization, the states $ \vert \xi \rangle _{s,a}$ and $ \vert \xi \rangle _{a,s}$ may be produced at the beamsplitter or a parametric downconverter output ports when the TMBS is on the input port.

Much work has demonstrated that photon addition and subtraction can bring about some markedly different physical properties from the original input states, so we shall investigate how the operations $a^{\dagger m}b^{n}$ and $a^{m}b^{\dagger n}$ influence the PND, the negativity of the WF and the entanglement of the states $\vert \xi \rangle_{s,a}$ and $ \vert \xi \rangle _{a,s}$ in the following several sections.

3 Photon Number Distribution

As a key characteristic of any two-mode quantum state $ \vert \phi \rangle $, its PND ($ \vert \langle n_{a},n_{b} \vert \phi \rangle \vert ^{2}$) refers to the probability of finding $n_{a}$ and $n_{b}$ photons in this field.^[26-27]

So, we\ now calculate the PNDs of the states $ \vert \xi \rangle _{s,a}$ and $ \vert \xi \rangle _{a,s}$ as

(6)$$ P_{s,a} =\mathcal{C}^{-1}\frac{ \vert \zeta \vert ^{2(n_{a}-m)}% }{(1+ \vert \zeta \vert ^{2})^{q}}\frac{q!n_{a}!}{((n_{a}% -m)!)^{2}n_{b}!}\delta_{n_{a}-m,q-n-n_{b}}\,, P_{a,s} =\mathcal{D}^{-1}\frac{ \vert \zeta \vert ^{2(n_{a}+m)}% }{(1+ \vert \zeta \vert ^{2})^{q}}\frac{q!n_{b}!}{((n_{b}% -n)!)^{2}n_{a}!}\delta_{n_{a}+m,q+n-n_{b}}\,, $$

which show that there exist the constrained condition, i.e., $n_{a}% -m=q-n-n_{b}$ or $n_{a}+m=q+n-n_{b}$, for the PNDs. In particular, when $m=n=0$, we have

(7)$$P_{s,a}=P_{a,s}==\begin{cases} \frac{ \vert \zeta \vert ^{2n_{a}}}{(1+ \vert \zeta \vert ^{2})^{q}}\frac{q!n_{a}!}{(n_{a}!)^{2}(q-n_{a})!},&\text{ }n_{a}=q-n_{b}, \\ 0,& n_{a}\neq q-n_{b}, \end{cases}$$

which is just the PND of the TMBS.

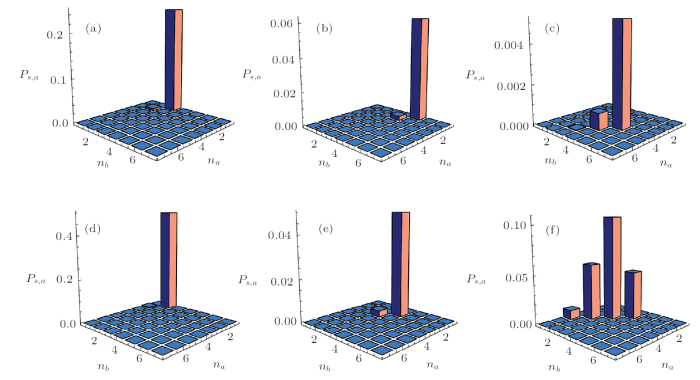
In Fig. 1, we plot the distribution $P_{s,a}$ in the Fock space ($n_{a},n_{b} $) for some different values of $q,m,n,$ and $\zeta$. From Fig. 1, we clearly see that the PND is constrained by the condition $n_{a}-m=q-n-n_{b}$ since the probabilities of finding only several ($n_{a},n_{b}$) numbers of photons in the field cannot be zero. As the parameters $m,n,$ and $q$ increase, the maximum probability of finding ($n_{a},n_{b}$) photons appears in different number states and the maximum probabilities are very different. As the parameter $\zeta$ is increased, more photons are presented in larger number states in this optical field, which is because the coefficient $c_{s,a}$ provides a higher weight to the initial higher-number photon component. In sum, the positions and values of the peaks depend on how many photons are added or subtracted, the two-mode number sum $q$ and the value of the parameter $\zeta$. A similar result appears for the distribution $P_{a,s}$ of the state $ \vert \xi \rangle _{a,s}$, so no more details here.

Fig. 1

New window|Download| PPT slide
Fig. 1(Color online) Photon number distribution $P_{s,a}$ for the state $\vert \xi \rangle _{s,a}$ in the Fock space ($n_{a},n_{b}$) for some different values of ($q,m,n,\varsigma$), where $(2,0,0,0.1),(4,0,0,0.1),(4,3,0,0.1),(4,0,3,0.1),(4,1,1,0.1),(4,1,1,0.6)$ respectively refer to (a), (b), (c), (d), (e), (f).

4 Wigner-Function Negativity

In quantum statistics, the negativity of WF is indeed a good indicator of the highly nonclassicality of the state.^[28-30] So, it is very essential for us to investigate the WFs for the states $ \vert \xi \rangle _{s,a}$ and $ \vert \xi \rangle _{a,s}$. In order to get the analytical expressions of the WFs for these two states, we first review the two-mode Wigner operator $\Delta ( \sigma_{,}\gamma ) $ in the entangled state $ \vert \vartheta \rangle $ representation,^[31-32] i.e.,

(8)$$ \Delta ( \sigma_{,}\gamma ) =\int \frac{d^{2}\vartheta}{\pi^{3} } \vert \sigma-\vartheta \rangle \langle \sigma+\vartheta \vert \exp ( \vartheta \gamma^{\ast}-\vartheta^{\ast}\gamma ), $$

where $ \vert \vartheta \rangle =e^{-({1}/{2}) \vert \vartheta \vert ^{2}+\vartheta a^{\dagger}-\vartheta^{\ast}b^{\dagger }+a^{\dagger}b^{\dagger}} \vert 00 \rangle $ is the entangled state, the parameter $\vartheta=\vartheta_{1}+$i$\vartheta_{2}$. Also, it can be easily proved that the states $ \vert \vartheta \rangle $ are the common eigen-states of the operators $( Q_{a}-Q_{b}) $ and $( P_{a}+P_{b}) $ with the eigenvalues $\sqrt{2}\vartheta_{1}$ and $\sqrt{2}\vartheta_{2}$, $Q_{i}$ and $P_{i}$ ($i=a,b$) are respectively the coordinate and momentum operators. Only when $\gamma=\alpha+\beta^{\ast}$ and $\sigma=\alpha-\beta^{\ast}$, there exists the identity $\Delta ( \sigma_{,}\gamma ) \equiv$ $\Delta ( \alpha_{,}\alpha^{\ast }) \Delta ( \beta_{,}\beta^{\ast}) $, where $\Delta ( i_{,}i^{\ast}) $ ($i=\alpha,\beta$) is the single-mode Wigner operator. Using Eqs. (4) and (8), the WFs for the states $ \vert \xi \rangle _{s,a}$ and $ \vert \xi \rangle _{a,s}$ are respectively obtained as

(9)$$ \mathcal{W}_{s,a}=\mathcal{C}^{-1}\sum_{l=0}^{q-n} \vert c_{s,a}% \vert ^{2}\mathcal{W}_{l+m,q-l-n},\\ &\mathcal{W}_{a,s} =\mathcal{D}^{-1}\sum_{l=m}^{q} \vert c_{a,s} \vert ^{2}% \mathcal{W}_{l-m,q-l+n}\,$$

where we have used the WF for the number state $\vert m,n \rangle$,i.e.,

(10)$$ \mathcal{W}_{m,n}=\frac{(-1)^{m+n}}{\pi^{2}}L_{m}( 4 \vert \alpha \vert ^{2}) L_{n}( 4 \vert \beta \vert ^{2}) e^{-2( \vert \alpha \vert ^{2}+ \vert \beta \vert ^{2}) }\,. $$

Obviously, when $m=n=0$, both the WFs $\mathcal{W}_{s,a}$ and $\mathcal{W}_{a,s}$ can reduce to the WF $\mathcal{W}_{q}$ for the TMBS, i.e.,

(11)$$ \mathcal{W}_{q}=\sum_{l=0}^{q}\frac{(-1)^{q} \vert c_{q} \vert ^{2} }{\pi^{2}}L_{l}( 4 \vert \alpha \vert ^{2}) L_{q-l}( 4 \vert \beta \vert ^{2}) \times e^{-2( \vert \alpha \vert ^{2}+ \vert \beta \vert ^{2}) }\,. $$

In Fig. 2, we plot the WF $\mathcal{W}_{s,a}$ for the state $ \vert \xi \rangle _{s,a}$ as a function of Re $\alpha$ and Re $\beta$ for different values of $m,n,q,$ and $\zeta$. Obviously, when $m=n=0$, the WF $\mathcal{W}_{q}$ has an upward main peak for even $q$ and a downward main peak for odd $q$, and the downward secondary peaks have regular distributions and their number is also related to the two-mode number sum $q$. As the parameters $m$ ($n=0$) and $\zeta$ increase, the regular distribution can be destroyed and develop into an irregular complex structure. However, the effects of the parameters $m$ and $\zeta$ on the WF distributions are different. In particular, the change of the parameter $\zeta$ cannot change the distributions of the main peak, but the direction of the main peak relies on the even or odd quality of two-mode number sum $q+m$. With the increasement of $n$ ($m=0$), the characteristics of the WF $\mathcal{W}_{s,a}$ for the two-mode number sum $q-n$ is consistent with that of the WF $\mathcal{W}_{q^{\prime}}$ for $q^{\prime}=q-n$, which is understandable by comparing the analytical expressions (3) and (4). For the the same number of operations ($m=n$), the WF distribution $\mathcal{W}_{s,a}$ depends entirely on the parameter $m$, but the direction of the main peak is only related to the two-mode number sum $q$. In sum, the parameters $m$ and $n$ lead to the increasingly complicated WF distributions, different from the original distributions $\mathcal{W}_{q}$. Noticing that the impacts of the parameters $m,n,q$ and $\zeta$ on the WF distribution $\mathcal{W}_{a,s}$ are very similar to the WF $\mathcal{W}_{a,s}$, so we cannot show it here.

Fig. 2

New window|Download| PPT slide
Fig. 2(Color online) Wigner function $\mathcal{W}_{s,a}$ for the state $\left \vert \xi \right \rangle_{s,a}$ of Re $\alpha$ and Re $\beta$ for different values of $(q,m,n,\varsigma)$, where $(2,0,0,0.1),(5,0,0,0.1),(5,0,0,0.6),(5,2,0,0.1),(5,3,0,0.1),(5,0,2,0.1),(5,0,3,0.1),(5,3,3,0.1)$ respectively refer to (a), (b), (c), (d), (e), (f), (g), (h).

In order to clearly see how the negativity of the WF $\mathcal{W}_{s,a}$ as an indicator for quantifying nonclassicality of the state $ \vert \xi \rangle _{s,a}$ changes with the parameters $m,n$ and $\zeta$, we adopt the integration formula for calculating the negative volume of the WF,^[33] that is,

(12)$$ \Delta=\frac{1}{2}\int d q d p[\vert W(p,q) \vert -W(p,q)]\,. $$

Inserting the WF (9) into the integration (12) and directly carrying out it, the negative volume $\Delta_{s,a}$ of the WF $\mathcal{W}_{s,a}$ can be easily obtained.

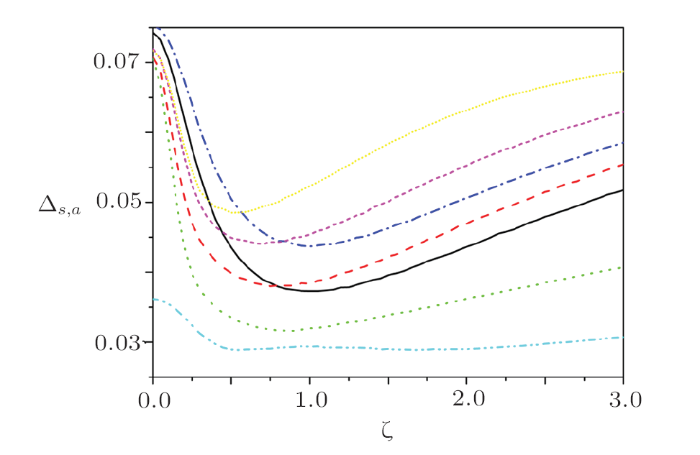
In Fig. 3, we present the negative volume $\Delta_{s,a}$ of the WF $\mathcal{W}_{s,a}$ for the state $\left \vert \xi \right \rangle _{s,a}$ for $q=5$ and the different values of $m$ and $n$. Clearly, the negative volume $\Delta_{s,a}$ decreases at first and then increases as the parameter $\zeta$ increases, which is independence on the photon numbers $m,n$. For $m=0$ ($n=0$) and any odd $n$ ($m$), the negative volume $\Delta_{s,a}$ of $\mathcal{W}_{s,a}$ is always smaller than that of $\mathcal{W}_{q}$ in the whole range of $\zeta$, which shows that the odd-number photon-addition or subtraction operations can weaken the nonclassicality of the original state $\left \vert \xi \right \rangle _{q}$ when another mode is zero. For any even $m$ ($n=0$) or the same number of operations (i.e., $m=n$), the negative volume $\Delta_{s,a}$ of $\mathcal{W}_{s,a}$ is smaller than that of $\mathcal{W}_{q}$ in the regime of low values of $\zeta$, but larger than that of $\mathcal{W}_{q}$ when the parameter $\zeta$ exceeds a certain threshold value. However, for any even $n$ ($m=0$), the negative volume $\Delta_{s,a}$ of $\mathcal{W}_{s,a}$ is always larger than that of $\mathcal{W}_{q}$ for all values of $\zeta$. In a word, the nonclassicality of the state $\left \vert \xi \right \rangle _{s,a}$ for the cases of $m=n$ or any even $m$ ($n=0$) and $n$ ($m=0$) can be enhanced for the initial state $\left \vert \xi \right \rangle _{q}$. Besides, the variations of the negative volume $\Delta_{a,s}$ of the WF $\mathcal{W}_{a,s}$ with the parameters $\zeta$, $m$, and $n$ are very similar to those of $\Delta_{s,a}$.

Fig. 3

New window|Download| PPT slide
Fig. 3(Color online) Negative volume $\Delta_{s,a}$ of the WF $\mathcal{W}_{s,a}$ for the state $\left \vert \xi \right \rangle _{s,a}$ for a give value of $q=5$ and different values of ($m,n$), where $(0,0),(2,0),(3,0),(0,2),(0,3),(2,2),(3,3)$ respectively refer to the black solid, red dashed, green dotted, blue dash-dotted, cyan dash-dot-dotted, magenta short-dashed, yellow short-dotted lines.

5 Entanglement

In this section, we want to discuss the entanglement properties of the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$ via calculating their Neumann entropy. For a pure entangled state $\left \vert \phi \right \rangle _{ab}$ with the Schmidt expansion,\ i.e., $\left \vert \phi \right \rangle _{ab}=\sum_{l=1}c_{l}\left \vert \alpha_{l}\right \rangle _{a}\left \vert \beta_{l}\right \rangle _{b}$, where $\left \vert \alpha _{l}\right \rangle _{a}$, $\left \vert \beta_{l}\right \rangle _{b}$ are the mutual orthonormal states and $c_{l}$ is some positive real number, its entanglement can be quantified by the partial von Neumann entropy of the reduced density operator, i.e., $E\left( \left \vert \phi \right \rangle _{ab}\right) =-$tr$(\rho_{a}\ln \rho_{a})=-\sum_{l=1}c_{l}^{2}\log_{2} c_{l}^{2}$, where $\rho_{a}=$ tr$_{b}\left( \left \vert \phi \right \rangle _{ab}\left \langle \phi \right \vert \right)$.^[34-35] Based on the Schmidt expressions of the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$ in Eq. (4), and thus their entanglement can be easily obtained as

(13)$$ E_{s,a}=-\sum_{l=0}^{q-n}\frac{\left \vert c_{s,a}\right \vert ^{2}} {\mathcal{C}}\log_{2}\frac{\left \vert c_{s,a}\right \vert ^{2}}{\mathcal{C}}\,, \\ E_{a,s}=-\sum_{l=m}^{q}\frac{\left \vert c_{a,s}\right \vert^{2} }{\mathcal{D}}\log_{2}\frac{\left \vert c_{a,s}\right \vert ^{2}}{\mathcal{D}}\,. $$

In the case of $m=n=0$, Eq. (13) refers to the amount of the entanglement of the state $\left \vert \xi \right \rangle _{q}$, i.e., $E_{q}=\sum_{l=0}^{q}\left \vert c_{q}\right \vert ^{2}\log_{2}\left \vert c_{q}\right \vert ^{2}$.

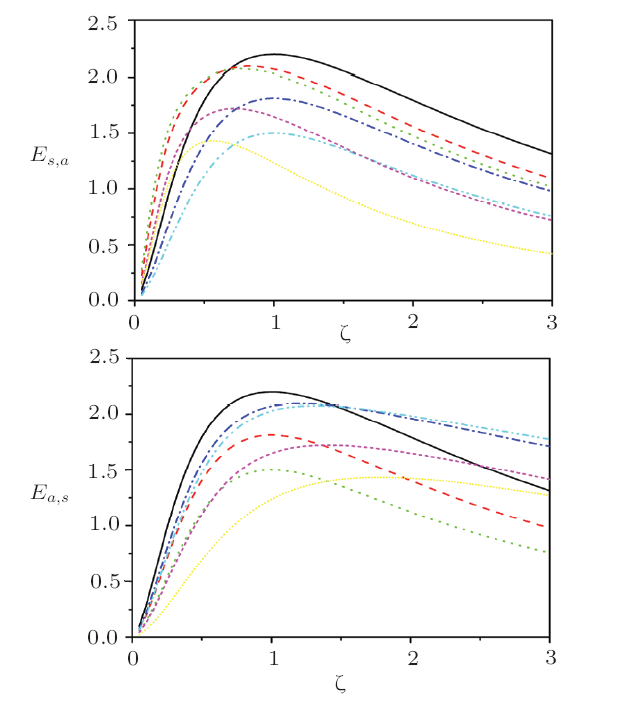
In Fig. 4, we plot the entanglement entropy as a function of the parameter $\zeta$ for the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$ with $q=5$ and different values of $m$ and $n$. Obviously, for any states $\left \vert \xi \right \rangle _{q}$, $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$, the entanglement always increases at first and then decreases as the parameter $\zeta$ increases, and their maximum values appear near $\zeta=1$. For both the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$, one-mode photon addition enhance the entanglement of the initial state $\left \vert \xi \right \rangle _{q}$, but one-mode photon subtraction weakens it. Comparing with the original state $\left \vert \xi \right \rangle _{q}$, the entanglement of the state $\left \vert \xi \right \rangle _{s,a}$ ($\left \vert \xi \right \rangle _{a,s}$) can be enhanced for smaller (larger) $\zeta$ when the same number of operations ($m=n$) is applied to both modes. With the increasement of the number of operations, the entanglement of the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$ decreases and totally less than that of $\left \vert \xi \right \rangle _{q}$ for enough large value of $m=n$.

Fig. 4

New window|Download| PPT slide
Fig. 4(Color online) Entanglement entropy as a function of the parameter $\varsigma$ for the states $\left \vert \xi \right \rangle _{s,a}$ and $\left \vert \xi \right \rangle _{a,s}$ with a given value of $q=5$ and different values of $(m,n)$, where the values of ($m,n$) are the same of those of Fig. 3.

6 Conclusions

In summary, we have investigated the PNDs, the WF distributions and the entanglement of two new multiple-photon-added and -subtracted TMBSs. The analytical results indicate that the PND is constrained by the condition $n_{a}-m=q-n-n_{b}$ or $n_{a}+m=q+n-n_{b}$, and the WF is represented as a finite dimensional summation over the WFs for the number states. Besides, the numerical results show that the different number of operations leads to different photon number distributions with the different positions and amplitudes of the maximum probabilities. For the initial state $\left\vert \xi \right \rangle_{q}$, both one-mode even-number photon operations and two-mode symmetrical operations can enhance its nonclassicality, and one-mode photon-addition and two-mode symmetrical operations can enhance its entanglement.

The authors have declared that no competing interests exist.

Reference By original order
By published year
By cited within times
By Impact factor

[1]

L. Y.

, Z. Y.

Liao

, M. S.

Zubairy

, Phys. Rev. A 95( 2017)012310.

[Cited within: 1]

[2]

Huang

, G.

, J.

Fang

, G.

Zeng

, Phys. Rev. A 87( 2013)012317.

[Cited within: 1]

[3]

Carranza

and C. C.

Gerry

, J. Opt. Soc. Am. B 29( 2012)2581.

[Cited within: 1]

[4]

Tipsmark

, J. S.

Neergaard-Nielsen

, U. L.

Andersen

, Opt. Express 21 ( 2013)6670.

[Cited within: 1]

[5]

Dell'Anno

, S.

De Siena

Adesso

and F.

Illuminati

, Phys. Rev. A 82 ( 2010)062316.

[6]

S. L.

Zhang

and P. van

Loock

, Phys. Rev. A 82 ( 2010)062316.

[Cited within: 1]

[7]

X. G.

Meng

, Z.

Wang

, J. S.

Wang

, H. Y.

Fan

, J. Opt. Soc. Am. B 29 ( 2012)3141.

[Cited within: 1]

[8]

X. G.

Meng

, J. S.

Wang

, B. L.

Liang

, C. X.

Han

,Front. Phys. 13 ( 2018)130322.

[9]

L. Y.

and H. Y.

Fan

, J. Opt. Soc. Am. B 25 ( 2008)1955.

[10]

X. G.

Meng

, Z.

Wang

, J. S.

Wang

, et al., J. Opt. Soc. Am. B 29 ( 2012)1844.

[11]

T. J.

Bartley

, P. J. D.

Crowley

, A.

Datta

, et al., Phys. Rev. A 87 ( 2013)022313.

DOI:10.1103/PhysRevA.87.022313 URL

[12]

Olivares

, M. G. A.

Paris

, R.

Bonifacio

, Phys. Rev. A 67 ( 2003)032314.

[13]

Kurochkin

, A. S.

Prasad

, A. I.

Lvovsky

, Phys. Rev. Lett. 112 ( 2014)070402.

[14]

Wang

, X. G.

Meng

, H. Y.

Fan

, J. Opt. Soc. Am. B 29 ( 2012)397.

[Cited within: 1]

[15]

Dell'Anno

, S. De

Siena

, F.

Illuminati

, Phys. Rep. 428( 2006)53.

[Cited within: 1]

[16]

M. S.

Kim

, J. Phys. B: At. Mol. Opt. Phys. 41 ( 2008)133001.

[Cited within: 1]

[17]

J. S.

Wang

, X. G.

Meng

, B. L.

Liang

,Chin. Phys. B 19 ( 2010)014207.

[Cited within: 1]

[18]

X. G.

Meng

, J. S.

Wang

, B. L.

Liang

,Chin. Phys. B 19 ( 2010)124205.

[Cited within: 1]

[19]

X. G.

Meng

, J. S.

Wang

, B. L.

Liang

, Opt. Commun. 283 ( 2010)4025.

[Cited within: 1]

[20]

J. S.

Wang

, H. Y.

Fan

, X. G.

Meng

, Chin. Phys. B 21 ( 2012)064204.

[Cited within: 1]

[21]

H. Y.

Fan

and L. Y.

, Opt. Commun. 281 ( 2008)5571.

[22]

Zhang

, X. G.

Meng

, C. X.

, J. S.

Wang

, J. Phys. Soc. Jpn. 87 ( 2018)024001.

[Cited within: 1]

[23]

Fiurasek

, Phys. Rev. A 80 ( 2009)053822.

[Cited within: 1]

[24]

S. L.

Zhang

and P. van

Loock

, Phys. Rev. A 82 ( 2010)062316.

[25]

M. S.

Kim

, J. Phys. B: At. Mol. Opt. Phys. 41 ( 2008)133001.

[Cited within: 1]

[26]

Schleich

, D. F.

Walls

, J. A.

Wheeler

, Phys. Rev. A 38 ( 1988)1177.

[Cited within: 1]

[27]

Wang

, X. G.

Meng

, H. Y.

Fan

, J. Phys. A: Math. Theor. 46 ( 2013)135305.

[Cited within: 1]

[28]

Hillery

, R. F.

O'Connell

, M. O.

Scully

, E. P.

Wigner

, Phys. Rep. 106 ( 1984)121.

[Cited within: 1]

[29]

W. P.

Schleich

, Quantum Optics in Phase Space
Wiley-VCH, Berlin ( 2001).

[30]

H. J.

Carmichael

, Statistical Methods in Quantum Optics 2: Non-Classical Fields
Springer-Verlag,Berlin ( 2007).

[Cited within: 1]

[31]

X. G.

Meng

, Z.

Wang

, J. S.

Wang

, H. Y.

Fan

, J. Opt. Soc. Am. B 30 ( 2013)1614.

DOI:10.1364/JOSAB.30.001614 URL [Cited within: 1]

[32]

H. Y.

Fan

, H. L.

, Y.

Fan

, Ann. Phys. 321 ( 2013)480.

[Cited within: 1]

[33]

Kenfack

and K.

Zyczkowski

, J. Opt. B: Quantum Semiclass. Opt. 6 ( 2004)396.

[Cited within: 1]

[34]

C. H.

Bennett

, H. J.

Bernstein

, S.

Popescu

, B.

Schumacher

,Phys. Rev. A 53 ( 1996)2046.

[Cited within: 1]

[35]

X. X.

,Phys. Rev. A 92 ( 2015)012318.

[Cited within: 1]