,2,3,*Corresponding authors: * E-mail:mofatzi@sci.cu.edu.eg
Received:2018-11-5Online:2019-04-1
Abstract
Keywords：
PDF (716KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ahmad Javid, Nauman Raza, M. S. Osman. Multi-solitons of Thermophoretic Motion Equation Depicting the Wrinkle Propagation in Substrate-Supported Graphene Sheets. [J], 2019, 71(4): 362-366 doi:10.1088/0253-6102/71/4/362
1 Introduction
Graphene in an isolated state has been explored in 2004 and since then it has procured attention of researchers all over the globe due to its exceptional properties. It is tested to be the hardest and thinnest nanoscale material consisting of a single layer of carbon atoms arranged in hexagonal filigree. Since all the atoms in graphene are surface atoms, therefore, it is quite responsive to mechanical, thermal, optical, and electronic effects,[1-7] which make it a key candidate for industrial applications.[8-11] Moreover, Quantum Hall effects are observed for graphene at moderate temperature.[12]Wrinkles have been observed in graphene sheets caused by scanning tunneling microscopy (STM) of graphene topographs on Si${\rm O}_2$ in Ref. [13]. Properties like electric conductivity and quantum transport are significantly affected by these wrinkle channels.[14-15] Wrinkles have been proved to be a good prospect in designing flexible electric sensors[16] and to assemble graphene nanoribbons.[17] Apart from these mentioned contributions, there are a lot of unaddressed issues like the absence of theoretical model depicting the formation process and the lack of knowledge to analyze the propagation properties of wrinkles.[18]
The well known KdV equation interprets the motion of single-soliton reads as
Solution of Eq. (1) is $u = 3vh^2(\sqrt{v}/2 )(x - vt)$, where $v$ portrays the velocity profile of soliton. The thermophoretic motion (TM) and shape of wrinkles in graphene are very akin to the solitary wave in its properties. In correspondence with Ref. [19], the structural shape of wrinkle at different positions derived through MD simulation by fitting a quadratic polynomial has the form: $u_w=3 c_w\,h^2\left((\sqrt{c_w}/2)[x-at^2/2-bt]\times c_w\right)$, where $a$ and $b$ are constants, and $c_w$ can be tailored to make $u_w$ consistent with the shape of the wrinkle. The motion equation satisfied by $u_w$ is given by
The wrinkle motion is in accordance with that of single-soliton as it remains unaffected during its course of motion. In a comparison of Eq. (2) with KdV equation, the additional term $(a t + b - c_w) (\partial u_w/\partial x)$ represents the driving force captured through thermal gradients and is held responsible for the acceleration of wrinkles.
Moreover, the motion of wrinkles in nanoribbons along with potential energy profile is discussed.[20] Through a numerical inspection, it is shown that the growth of buckling-driven wrinkles in graphene monolayers heavily depends on size and chirality.[21]
A number of techniques have been developed to study the integrability and to construct multiple-solitary wave solutions of nonlinear partial differential equations including inverse scattering,[22-24] Hirota's bilinear method and its simplified form.[25-30] In Refs. [29-30], Eq. (2) was investigated to study the wave propagation of the N-soliton solutions. These solutions have been derived via Hirota's bilinear method with the aid of symbolic computations. Furthermore, the shape, amplitude, open direction and width of the N-solitons are controllable through certain parameters.
The theme of this paper is to use the generalized unified method,[31-33] which is the generalization of the simple unified method presented in Refs. [34-37]. The paper is categorized in three sections. Section 2 is devoted to the study of multi-soliton solution of the TM equation along with their graphics using the GUM. We will conclude our paper in Sec. 3.
2 Multi-soliton Solutions of TM Equation by GUM
In this section, we use the GUM[31-33] to yield muti-soliton solutions of thermophoretic given by Eq. (2). We use a dependent variable transformation $u(x, t) = \Omega_x(x, t)$ in Eq. (2). By integrating both sides with respect to $x$ and taking integration constants to be zero, we obtainHere, we use the GUM to find single-soliton solutions of Eq. (2) (In this case we use the unified method,[34-37] which is a special case of the GUM). We assume that
where $\xi_1=\alpha_1x+\int\alpha_2(t) {\rm d}t$. Here $p_0,p_1,q_0$ and $q_1$ are unknowns to be determined. By inserting Eq. (4) into Eq. (3) and equating the coefficients of $\psi_i(\xi_i)$ to zero gives a system of algebraic equations whose solution is given by
Using Eq. (5) along with auxiliary function $\psi_1(\xi_1)$ in Eq. (4), we get
As $u(x,t)=\Omega_x(x,t)$, so we have
It is quite evident that the one-soliton solution in Eq. (7) can be compared to that reported in Ref. [19] for
$c_w=c_1^2\alpha_1^2$.
2.2 2-soliton Solutions of TM Equation
In this subsection, we find the two-soliton solutions of Eq. (2) using the GUM.[31-33] Let us assume that
where $\xi_1 = \alpha_1x+\int\alpha_2(t) {\rm d}t, \xi_2 = \beta_1x+\int\beta_2(t){\rm d}t$ and $p_i$ and $q_i$ are arbitrary parameters to be evaluated, $i=0,1,2$. The functions $\psi_i(\xi_i)$ are obtained from the first order differential equations $\psi_1^{\prime}(\xi_1) = b_1\psi_1(\xi_1)$ and $\psi_2^{\prime}(\xi_2) = c_1\psi_2(\xi_2)$. By plugging Eq. (8) into Eq. (3) and by equating the coefficients of $\psi_i(\xi_i)$ to zero, we get a system of algebraic equations whose solution is given by
\begin{eqnarray}\label{solution_2}\nonumber p_0&=&-12\alpha_1b_1q_0+\frac{S^2_{-}p_1q_2}{S^2_{+}q_3}\,,\quad p_2=\frac{q_2\left(S^2_{-}p_1q_2/S^2_{+}q_3-12q_0S_{-}\right)}{q_0}\,,\quad p_3=\frac{q_2S^2_{-}\left(p_1+12\beta_1c_1q_3q_0S^2_{+}/q_2S^2_{-}\right)}{q_0S^2_{+}},\\\nonumber q_1&=&\frac{q_3q_0S^2_{+}}{q_2S^2_{-}}\,,\quad \alpha_2(t)=-\alpha_1(a t+b+b^2_1\alpha^2_1-c_w)\,,\quad \beta_2(t)=-\beta_1(a t+b+c^2_1\beta^2_1-c_w), \end{eqnarray}
where $S_{\pm}=\alpha_1b_1\pm\beta_1c_1$.
By utilizing the above solution into Eq. (8), we get the solution of Eq. (2) namely,
where $\xi_1=\alpha_1x-\alpha_1(a t/2+b+b^2_1\alpha^2_1-c_w)t,~\xi_2=\beta_1x-\beta_1(at/2+b+c^2_1\beta^2_1-c_w)t.$ The solution is depicted graphically in Fig. 1 for different values of the parameters.
Fig. 1
New window|Download| PPT slideFig. 1Evolution of two solitons: (a) 3D-plot (b) The projection view of (a), for $c_1=1/2,~b_1=3,~q_2=1/5,~q_0=1/20,~c_w=1/10,~p_1=3/20,~\alpha_1=1,~\beta_1=2,~a=0.3,~b=-0.5,~q_3=1$.
In this case, the GUM[31-33] asserts that
where $i < j$ and $\xi_1=\alpha_1x+\int\alpha_2(t) {\rm d}t,~\xi_2=\beta_1x+\int\beta_2(t){\rm d}t, ~\xi_3=\gamma_1x+\int\gamma_2(t) {\rm d}t$ and $p_i,~p_{ij},~p_{123}$ as well as $q_i,~q_{ij},~q_{123}$ are arbitrary constants to be evaluated, while $i,j=1,2,3$. The auxiliary functions $\psi_i(\xi_i)$ satisfy $\psi_1^{\prime}(\xi_1) = b_1\psi_1(\xi_1)$, $\psi_2^{\prime}(\xi_2) = c_1\psi_2(\xi_2)$, and $\psi_3^{\prime}(\xi_3) = s_1\psi_3(\xi_3)$. By plugging Eq. (10) into Eq. (3) and by equating the coefficients of $\psi_i(\xi_i)$ and $\psi_i(\xi_i)\psi_j(\xi_j)$ to zero, we get a system of algebraic equations whose solution is given by
$$ p_0 = \frac{1}{H^2_{+}R^2_{+}q_{123}}[-12b^5_1\alpha^5_1q_0q_{123}+c^2_1\beta^2_1p_1q_{23}\gamma^2_1s^2_1 +b^4_1\alpha^4_1(p_1q_{23}-24q_{123}q_0T_{+}) +b^2_1\alpha^2_1(p_1q_{23}\gamma^2_1s^2_1+c^2_1\beta^2_1(p_1q_{23}-24q_{123}q_0\gamma_1s_1) \\ +4c_1\beta_1\gamma_1s_1(p_1q_{23}-6q_{123}q_0\gamma_1s_1)) -2b_1c_1\alpha_1\beta_1\gamma_1s_1(p_1q_{23}\gamma_1s_1+c_1\beta_1 (p_1q_{23}+6q_{123}q_0\gamma_1s_1))-2b^3_1\alpha^3_1(6c_1^2\beta_1^2q_{123}q_0 \\ +\gamma_1s_1(p_1q_{23}+6q_{123}q_0\gamma_1s_1)+c_1\beta_1 (p_1q_{23}+24q_{123}q_0\gamma_1s_1))], \\ p_2 =-\frac{1}{H^2_{+}T^2_{+}R^2_{+}q_{123}q_3}[q_{23}H_{-}T^2_{+} (12b_1^4\alpha_1^4q_{123}q_0+c_1\beta_1(p_1q _{23}+12c_1\beta_1q_{123}q_0))\gamma_1^2s_1^2 +b_1\alpha_1\gamma_1s_1(-2c_1\beta_1p_1q_{23}+24c_1^2 \beta_1^2q_{123}q_0 \\ -p_1q_{23}\gamma_1s_1+24c_1\beta_1q_{123}q_0\gamma_1s_1) +b_1^3\alpha_1^3(-p_1q_{23}+24q_{123}q_0T_{+}) +b_1^2\alpha_1^2(12c_1^2\beta_1^2q_{123}q_0+2\gamma_1s_1(p_1q_{23} +6q_{123}q_0\gamma_1s_1) \\ +c_1\beta_1(p_1q_{23}+48q_{123}q_0\gamma_1s_1))]\,, \\ p_3=-\frac{q_3R_{-}}{H^2_{+}R^2_{+}q_{123}q_0}[12b_1^4\alpha_1^4q_{123}q_0+c_1^2\beta_1^2\gamma_1s_1 (p_1q_{23}+12q_{123}q_0\gamma_1s_1)+b_1^3\alpha_1^3(-p_1q_{23}+24q_{123}q_0T_{+}) +b_1c_1\alpha_1\beta_1(2\gamma_1s_1(-p_1q_{23} \\ +12q_{123}q_0\gamma_1s_1)+c_1\beta_1(-p_1q_{23}+24q_{123}q_0\gamma_1s_1)) +b_1\alpha_1^2(12c_1^2\beta_1^2q_{123}q_0 \\ +\gamma_1s_1(p_1q_{23}+12q_{123}q_0\gamma_1s_1)+2c_1\beta_1(p_1q_{23} +24q_{123}q_0\gamma_1s_1))]\,, \\ p_{12}=\frac{H^2_{-}T^2_{+}q_{23}(p_1+12c_1\beta_1 (H^2_{+}R^2_{+}q_0q_{123})/H^2_{-}R^2_{-}q_{23})}{H^2_{+}T^2_{-}q_{3}}\,, \\ p_{13}=\frac{q_3R^2_{-}(p_1+12H^2_{+}R^2_{+}q_0q_{123}\gamma_1s_1/H^2_{-}R^2_{-}q_{23})}{q_0R^2_{+}}\,, \\ p_{23}=\frac{q_{23}}{H^2_{+}R^2_{+}q_0q_{123}}\bigl[-12b_1^5\alpha_1^5q_0q_{123}+b_1^4 \alpha_1^4(p_1q_{23}-12q_{123}q_0T_{+})+c_1^2\beta_1^2\gamma_1^2s_1^2(p_1q_{23}+12q_{123}q_0T_{+}) +2b_1^3\alpha_1^3(-c_1\beta_1p_1q_{23} \\ +6c_1^2\beta_1^2q_{123}q_0+\gamma_1s_1(-p_1q_{23} +6q_{123}q_0\gamma_1s_1)) +2b_1c_1\alpha_1\beta_1\gamma_1s_1(12c_1^2\beta_1^2q_{123}q_0 +\gamma_1s_1(-p_1q_{23}+12q_{123}q_0\gamma_1s_1) \\ +c_1\beta_1(-p_1q_{23}+18q_{123}q_0\gamma_1s_1))+b_1^2\alpha_1^2(12c_1^3\beta_1^3q_{123}q_0 +4c_1\beta_1\gamma_1s_1(p_1q_{23}+9q_{123}q_0\gamma_1s_1) +\gamma_1^2s_1^2(p_1q_{23}+12q_{123}q_0\gamma_1s_1) \\ +c_1^2\beta_1^2(p_1q_{23}+36q_{123}q_0\gamma_1s_1))\bigr]\,, \\ p_{123}=\frac{1}{H^2_{+}R^2_{+}q_0}[2b_1^3\alpha_1^3T_{+}(-p_1q_{23}+12q_{123}q_0T_{+}) +2b_1c_1\alpha_1\beta_1\gamma_1s_1T_{+}(-p_1q_{23}+12q_{123}q_0T_{+}) b_1^4\alpha_1^4(p_1q_{23}+12q_{123}q_0T_{+}) \\ +c_1^2\beta_1^2\gamma_1^2s_1^2(p_1q_{23}+12q_{123}q_0T_{+}) +b_1^2\alpha_1^2(c_1^2\beta_1^2+4c_1\beta_1\gamma_1s_1+\gamma_1^2s_1^2) (-p_1q_{23}+12q_{123}q_0T_{+})]\,, \\ q_1=\frac{H^2_{+}R^2_{+}q_0q_{123}}{H^2_{-}R^2_{-}q_{23}}\,,\quad\quad q_2 =\frac{T^2_{+}q_0q_{23}}{T^2_{-}}\,,\quad\quad q_{13}=\frac{H^2_{+}q_3q_{123}}{H^2_{-}}\,, \quad\quad q_{12}=\frac{q_{123}q_0R^2_{+}T^2_{+}}{q_3R^2_{-}T^2_{-}}\,, \\ \alpha_2(t)=-\alpha_1(a t+b+b_1^2\alpha_1^2-c_w)\,,\quad\quad \beta_2(t)=-\beta_1(a t+b+c_1^2\beta_1^2-c_w)\,,\quad\quad \gamma_2(t)=-\gamma_1(a t+b+r_1^2s_1^2-c_w)\,, $$
where $H_{\pm}=b_1\alpha_1\pm c_1\beta_1,~R_{\pm}=b_1\alpha_1\pm \gamma_1s_1,~T_{\pm}=c_1\beta_1\pm \gamma_1s_1.$
Extracting $\psi_i(\xi_i)$ from $\psi^{\prime}_i(\xi_i)=c_i\psi_i(\xi_i)$ and putting them into Eq. (10) along with the values of the parameters, we get the solution of Eq. (2) which is not written here because of its huge volume. The solution is depicted graphically in Fig. 2 for different values of the parameters.
Fig. 2
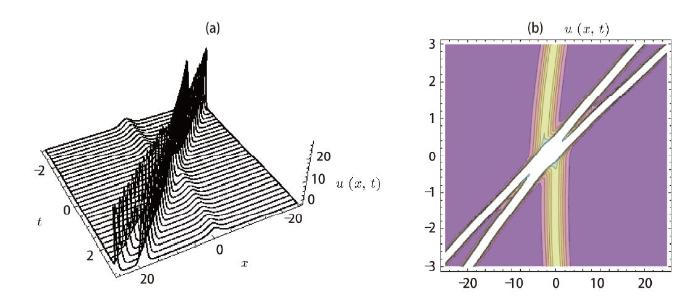New window|Download| PPT slideFig. 2Evolution of three solitons: (a) 3D-plot (b) The projection view of (a), for $c_1=1/2,~b_1=3,~s_{1}=0.9~q_{123}=1/5,~q_0=1/20,~c_w=1/10,~p_1=3/20,~\alpha_1=-1, ~\beta_1=2,~\gamma_1=3,~a=0.3,~b=-0.5,~q_3=1,~q_{23}=1$.
3 Conclusion
This paper investigates the multi-soliton solutions for TM equation, which describes the thermophoresis of wrinkles in graphene sheets. The versatile integration tools, the GUM, is applied to extract 2- and 3-soliton solutions. These solutions are analyzed graphically and it is observed that the width, amplitude, shape and open direction depends on certain parameters. In physical experiments, the single soliton serves as an analogue to simulate the propagation for single wrinkle wave.[19] Therefore, multi-solitons can provide a valuable insight to understand the dynamics of multiple wrinkle waves in graphene nanoribbons. Comparing with the results in Refs. [29-30], we found that: in our paper the obtained solutions had different wave structures and the interaction between these solutions represents an elastic collision. The solutions can be critical to understand attributes of the TM equation through the wonder nano-material graphene sheet.Compliance with Ethical Standards
Conflict of interests: The authors declare that they have no conflict of interests.
Reference By original order
By published year
By cited within times
By Impact factor
DOI:10.1126/science.1136836URLPMID:17255506409300143002282013 [Cited within: 1]
Nanoelectromechanical systems were fabricated from single- and multilayer graphene sheets by mechanically exfoliating thin sheets from graphite over trenches in silicon oxide. Vibrations with fundamental resonant frequencies in the megahertz range are actuated either optically or electrically and detected optically by interferometry. We demonstrate room-temperature charge sensitivities down to 8 脳$10^{-4}$electrons per root hertz. The thinnest resonator consists of a single suspended layer of atoms and represents the ultimate limit of two-dimensional nanoelectromechanical systems.
DOI:10.1126/science.1157996URL
DOI:10.1088/0957-4484/21/16/165204URLPMID:20351404
We use suspended graphene electromechanical resonators to study the variation of resonant frequency as a function of temperature. Measuring the change in frequency resulting from a change in tension, from 300 to 30 K, allows us to extract information about the thermal expansion of monolayer graphene as a function of temperature, which is critical for strain engineering applications. We find that thermal expansion of graphene is negative for all temperatures between 300 and 30 K. We also study the dispersion, the variation of resonant frequency with DC gate voltage, of the electromechanical modes and find considerable tunability of resonant frequency, desirable for applications like mass sensing and RF signal processing at room temperature. With a lowering of temperature, we find that the positively dispersing electromechanical modes evolve into negatively dispersing ones. We quantitatively explain this crossover and discuss optimal electromechanical properties that are desirable for temperature-compensated sensors.
DOI:10.1016/j.commatsci.2013.03.009URL
The electromechanical responses of a graphene nanoribbon, such as its ripple magnitude, bending rigidity and effective spring constant, were investigated via classical molecular dynamics simulations and the elastic plate theory with a view to future engineering applications of graphene-nanoribbon-based nanoelectromechanical devices. While the bending rigidity was low for large ripples, it was high for very small ripples. However, on most ripple scales, the values of the bending rigidity remained constant around 2.3eV. The bending rigidity gradually increased from about 1.2 to 2.37eV with increasing deflection, after that, the bending rigidity slightly decreased to 2.29eV with further increases in deflection, and finally rapidly increased to 2.93eV with increasing deflection until the breaking point. The effective spring constant increased to 0.36N/m with increasing applied force and deflection, in the linear elastic region it remained below 0.25N/m.
DOI:10.1038/nmat3542URLPMID:23334002
Crumpled graphene films are broadly used, for instance in electronics1, energy storage2,3, composites4,5, and biomedicine6. Although it is known that the degree of crumpling affects graphene's properties and the performance of graphene-based devices and materials3,5,7, the controlled folding and unfolding of crumpled graphene films has not been demonstrated. Here we report an approach to reversibly control the crumpling and unfolding of large-area graphene sheets. We show with experiments, atomistic simulations and theory that, by harnessing the mechanical instabilities of graphene adhered on a biaxially pre-stretched polymer substrate and by controlling the relaxation of the pre-strains in a particular order, graphene films can be crumpled into tailored self-organized hierarchical structures that mimic superhydrophobic leaves. The approach enables us to fabricate large-area conductive coatings and electrodes showing superhydrophobicity, high transparency, and tunable wettability and transmittance. We also demonstrate that crumpled graphene-polymer laminates can be used as artificial-muscle actuators.
DOI:10.1016/j.carbon.2013.05.052URL [Cited within: 1]
This review discusses the genesis of impermeability in graphene and its extraordinary applications in fluid-encasement for wet electron-microscopy, selective gas-permeation, nanopore-bio-diffusion, and barrier coating against rusting and environmental hazards. As the thinnest material, graphene is composed of sp(2) hybridized carbon atoms linked to one another in a 2D honeycomb lattice with high electron-density in its aromatic rings, which blocks-off all molecules. This phenomena, in combination with its strong structure (C-C bond energy = 4.9 eV and intrinsic strength = 43 N/m) makes graphene the most impermeable membrane (thinnest membrane that is impermeable). Apart from the applications mentioned above, graphene coatings have enabled fundamental studies on chemical processes and fluid structures. For example, graphene can allow electron imaging of nanocrystal nucleation process and water-lattice-structure due to its impermeability. Along with being the strongest, most conductive, and optically-absorbing material (similar to 2.3% optical absorbance), graphene's impermeability opens a wide range of exciting opportunities. (c) 2013 Elsevier Ltd. All rights reserved.
DOI:10.1038/nchem.2515URLPMID:27325100 [Cited within: 1]
Abstract One- and two-dimensional carbon nanomaterials are attracting considerable attention because of their extraordinary electrical, mechanical and thermal properties, which could lead to a range of important potential applications. Synthetic processes associated with making these materials can be quite complex and also consume large amounts of energy, so a major challenge is to develop simple and efficient methods to produce them. Here, we present a self-templated, catalyst-free strategy for the synthesis of one-dimensional carbon nanorods by morphology-preserved thermal transformation of rod-shaped metal-organic frameworks. The as-synthesized non-hollow (solid) carbon nanorods can be transformed into two- to six-layered graphene nanoribbons through sonochemical treatment followed by chemical activation. The performance of these metal-organic framework-derived carbon nanorods and graphene nanoribbons in supercapacitor electrodes demonstrates that this synthetic approach can produce functionally useful materials. Moreover, this approach is readily scalable and could be used to produce carbon nanorods and graphene nanoribbons on industrial levels.
DOI:10.1002/adma.201506410URLPMID:27273554
Abstract The possibility to produce and process graphene, related 2D crystals, and heterostructures in the liquid phase makes them promising materials for an ever-growing class of applications as composite materials, sensors, in flexible optoelectronics, and energy storage and conversion. In particular, the ability to formulate functional inks with on-demand rheological and morphological properties, i.e., lateral size and thickness of the dispersed 2D crystals, is a step forward toward the development of industrial-scale, reliable, inexpensive printing/coating processes, a boost for the full exploitation of such nanomaterials. Here, the exfoliation strategies of graphite and other layered crystals are reviewed, along with the advances in the sorting of lateral size and thickness of the exfoliated sheets together with the formulation of functional inks and the current development of printing/coating processes of interest for the realization of 2D-crystal-based devices.
DOI:10.1016/j.pmatsci.2016.04.001URL
Silicene, a silicon analogue of graphene, has attracted increasing attention during the past few years. As early as in 1994, the possibility of stage corrugation in the Si analogs of graphite had already been theoretically explored. But there were very few studies on silicene until 2009, when silicene with a low buckled structure was confirmed to be dynamically stable byab initiocalculations. In spite of the low buckled geometry, silicene shares most of the outstanding electronic properties of planar graphene (e.g., the irac cone , high Fermi velocity and carrier mobility). Compared with graphene, silicene has several prominent advantages: (1) a much stronger spin rbit coupling, which may lead to a realization of quantum spin Hall effect in the experimentally accessible temperature, (2) a better tunability of the band gap, which is necessary for an effective field effect transistor (FET) operating at room temperature, (3) an easier valley polarization and more suitability for valleytronics study. From 2012, monolayer silicene sheets of different superstructures were successfully synthesized on various substrates, including Ag(111), Ir(111), ZrB2(0001), ZrC(111) and MoS2surfaces. Multilayer silicene sheets have also been grown on Ag(111) surface. The experimental successes have stimulated many efforts to explore the intrinsic properties as well as potential device applications of silicene, including quantum spin Hall effect, quantum anomalous Hall effect, quantum valley Hall effect, superconductivity, band engineering, magnetism, thermoelectric effect, gas sensor, tunneling FET, spin filter, and spin FET, etc. Recently, a silicene FET has been fabricated, which shows the expected ambipolar Dirac charge transport and paves the way towards silicene-based nanoelectronics. This comprehensive review covers all the important theoretical and experimental advances on silicene to date, from the basic theory of intrinsic properties, experimental synthesis and characterization, modulation of physical properties by modifications, and finally to device explorations.
DOI:10.1016/j.bios.2016.06.045URLPMID:27373809 [Cited within: 1]
61Graphene-like 2D nanomaterials are promising in designing functional biointerfaces.61We review graphene-like 2D nanomaterial-based electrochemical sensors.61We review graphene-like 2D nanomaterial-based fluorescent sensors.61Rational design of novel graphene-like nanomaterial-based biointerfaces is summarized.
DOI:10.1126/science.1137201URLPMID:17303717 [Cited within: 1]
The quantum Hall effect (QHE), one example of a quantum phenomenon that occurs on a truly macroscopic scale, has attracted intense interest since its discovery in 1980 and has helped elucidate many important aspects of quantum physics. It has also led to the establishment of a new metrological standard, the resistance quantum. Disappointingly, however, the QHE has been observed only at liquid-helium temperatures. We show that in graphene, in a single atomic layer of carbon, the QHE can be measured reliably even at room temperature, which makes possible QHE resistance standards becoming available to a broader community, outside a few national institutions.
DOI:10.1021/nl902729pURLPMID:19852488 [Cited within: 1]
We report on the scanning tunneling microscopy study of a new class of corrugations in exfoliated monolayer graphene sheets, that is, wrinkles similar to 10 nm in width and similar to 3 nm in height. We found such corrugations to be ubiquitous in graphene and have distinctly different properties when compared to other regions of graphene. In particular, a "three-for-six" triangular pattern of atoms is exclusively and consistently observed on wrinkles, suggesting the local curvature of the wrinkle provides a sufficient perturbation to break the 6-fold symmetry of the graphene lattice. Through scanning tunneling spectroscopy, we further demonstrate that the wrinkles have lower electrical conductance and are characterized by the presence of midgap states, which is in agreement with recent theoretical predictions. The observed wrinkles are likely important for understanding the electrical properties of graphene.
DOI:10.1021/nl300183eURLPMID:22468807 [Cited within: 1]
We report a novel mechanical response of few-layer graphene, h-BN, and MoS(2) to the simultaneous compression and shear by an atomic force microscope (AFM) tip. The response is characterized by the vertical expansion of these two-dimensional (2D) layered materials upon compression. Such effect is proportional to the applied load, leading to vertical strain values (opposite to the applied force) of up to 150%. The effect is null in the absence of shear, increases with tip velocity, and is anisotropic. It also has similar magnitudes in these solid lubricant materials (few-layer graphene, h-BN, and MoS(2)), but it is absent in single-layer graphene and in few-layer mica and Bi(2)Se(3). We propose a physical mechanism for the effect where the combined compressive and shear stresses from the tip induce dynamical wrinkling on the upper material layers, leading to the observed flake thickening. The new effect (and, therefore, the proposed wrinkling) is reversible in the three materials where it is observed.
DOI:10.1021/nl300563hURL [Cited within: 1]
DOI:10.1021/nn103523tURLPMID:21452882 [Cited within: 1]
In this study, we report a buckling approach for graphene and graphene ribbons on stretchable elastomeric substrates. Stretched polydimethylsiloxane (PDMS) films with different prestrains were used to receive the transferred graphene, and nanoscale periodical buckling of graphene was spontaneously formed after strain release. The morphology and periodicity of the as-formed graphene ripples are dependent strongly on their original shapes and substrates' prestrains. Regular periodicity of the ripples preferred to form for narrow graphene ribbons, and both the amplitude and periodicity are reduced with the increase of prestrain on PDMS. The graphene ripples have the ability to afford large strain deformation, thus making it ideal for flexible electronic applications. It was demonstrated that both graphene ribbon and nanographene film ripples could be used for strain sensors, and their resistance changes upon different strains were studied. This simple and controllable process of buckled graphene provides a feasible fabrication for graphene flexible electronic devices and strain sensors due to its novel mechanical and electrical properties.
[Cited within: 1]
DOI:10.1016/j.mattod.2015.10.002URL [Cited within: 1]
Distinctive from their 1D and 0D counterparts, 2D nanomaterials (2DNs) exhibit surface corrugations (wrinkles and ripples) and crumples. Thermal vibrations, edge instabilities, thermodynamically unstable (interatomic) interactions, strain in 2D crystals, thermal contraction, dislocations, solvent trapping, pre-strained substrate-relaxation, surface anchorage and high solvent surface tension during transfer cause wrinkles or ripples to form on graphene. These corrugations on graphene can modify its electronic structure, create polarized carrier puddles, induce pseudomagnetic field in bilayers and alter surface properties. This review outlines the different mechanisms of wrinkle, ripple and crumple formation, and the interplay between wrinkles and ripples attributes (wavelength/width, amplitude/height, length/size, and bending radius) and graphene's electronic properties and other mechanical, optical, surface, and chemical properties. Also included are brief discussions on corrugation-induced reversible wettability and transmittance in graphene, modulation of its chemical potential, enhanced energy storage and strain sensing via relaxation of corrugations. Finally, the review summarizes the future areas of research for 2D corrugations and crumples.
DOI:10.1039/c2nr32580bURLPMID:23166021 [Cited within: 3]
We studied the thermophoretic motion of wrinkles formed in substrate-supported graphene sheets by nonequilibrium molecular dynamics simulations. We found that a single wrinkle moves along applied temperature gradient with a constant acceleration that is linearly proportional to temperature deviation between the heating and cooling sides of the graphene sheet. Like a solitary wave, the atoms of the single wrinkle drift upwards and downwards, which prompts the wrinkle to move forwards. The driving force for such thermophoretic movement can be mainly attributed to a lower free energy of the wrinkle back root when it is transformed from the front root. We establish a motion equation to describe the soliton-like thermophoresis of a single graphene wrinkle based on the Korteweg-de Vries equation. Similar motions are also observed for wrinkles formed in a Cu-supported graphene sheet. These findings provide an energy conversion mechanism by using graphene wrinkle thermophoresis.
DOI:10.1088/0022-3727/47/34/345307URL [Cited within: 1]
Graphene is a two-dimensional, one-atom thick carbon nano-polymorph with a unique combination of physical and mechanical properties promising for many applications. Compressive in-plane stresses can result in the formation of wrinkles in a graphene sheet. Elastic strain and wrinkles are often used to control various physical properties of graphene. Wrinklon is a transition zone where two or more wrinkles merge into one. In this study, by means of molecular dynamics simulations, the potential energy density and amplitude of unidirectional wrinkles in suspended graphene are calculated as the functions of their wavelength for a given in-plane strain. Overdamped motion of wrinklons along graphene nanoribbons of different widths is studied. The shape and potential energy of wrinklons as well as elastic strain in the vicinity of wrinklons are calculated. The results of the present study should lead to a better understanding of suspended graphene devices and the effect of wrinkle dynamics on the electronic properties of graphene.
DOI:10.1088/0957-4484/26/6/065701URLPMID:25597449 [Cited within: 1]
Abstract We theoretically and numerically investigate the growth of buckling-driven wrinkles in graphene monolayers. It is found that the growth of buckling-driven wrinkles in a graphene monolayer is remarkably chirality- and size-dependent. In small sizes, the flexural response of a graphene sheet cannot be accurately described by the classical Euler regime, and the non-continuum effect leads to zigzag-along-preferred buckling. With the increase of size, the width/length ratio α of the compressed region plays an important role in the growth of buckling-driven wrinkles. When α02023.0, the non-continuum effect and chiral bending stiffness can both be neglected, and the buckling in a graphene monolayer is isotropic. The chirality-along-preferred transition of compressed buckling in a graphene monolayer leads to an improved fundamental understanding of the dynamics mechanism of graphene-based nanodevices, especially for the nanodevices with high frequency response.
DOI:10.1103/PhysRevLett.19.1095URL [Cited within: 1]
[Cited within: 1]
DOI:10.1103/PhysRevLett.27.1192URL [Cited within: 1]
An exact solution has been obtained for the Korteweg-de Vries equation for the case of multiple collisions of N solitons with different amplitudes.
DOI:10.1063/1.527733URL
Bell’s inequalities are briefly presented in the context of order‐unit spaces and then studied in some detail in the framework ofC*‐algebras. The discussion is then specialized to quantum field theory. Maximal Bell correlations β(φ,A(O1),A(O2))for two subsystems localized in regionsO1andO2and constituting a system in the state φ are defined, along with the concept of maximal Bell violations. After a study of these ideas in general, properties of these correlations in vacuum states of arbitrary quantum field models are studied. For example, it is shown that in the vacuum state the maximal Bell correlations decay exponentially with the product of the lowest mass and the spacelike separation ofO1andO2. This paper is also preparation for the proof in Paper II [S. J. Summers and R. Werner, J. Math. Phys.28, 2448 (1987)] that Bell’s inequalities are maximally violated in the vacuum state.
DOI:10.1166/nnl.2018.2629URL [Cited within: 2]
[Cited within: 3]
[Cited within: 4]
DOI:10.1007/s11071-018-4222-1
DOI:10.1080/09205071.2018.1445039URL [Cited within: 4]
In this work, we construct multi-soliton solutions of the (2+ 1)-dimensional breaking soliton equation with variable coefficients by using the generalized unified method. We employ this method to obtain double- and triple- soliton solutions. Furthermore, we study the nonlinear interactions between these solutions in a graded-index waveguide. The physical insight and the movement role of the... [Show full abstract]
DOI:10.1007/s10955-012-0467-0URL [Cited within: 2]
AbstractWe present a brief report on the different methods for finding exact solutions of nonlinear evolution equations. Explicit exact traveling wave solutions are the most amenable besides implicit and parametric ones. It is shown that most of methods that exist in the literature are equivalent to the “generalized mapping method” that unifies them. By using this method a class of formal exact solutions for reaction diffusion equations with finite memory transport is obtained. Attention is focused to the finite-memory-transport-Fisher and Nagumo equations.
DOI:10.7566/JPSJ.82.044004URL
DOI:10.1007/s13226-014-0047-xURL
Recently the unified method for finding traveling wave solutions of nonlinear evolution equations was proposed by one of the authors. It was shown that, this method unifies all the methods being used to find these solutions. In this paper, we extend this method to find a class of formal exact solutions to Korteweg-de Vries equation with space-time dependent coefficients.
DOI:10.1007/s11082-018-1346-yURL [Cited within: 2]
This paper investigates the coupled Schr02dinger–Boussinesq equation with variable-coefficients using the unified method. New nonautonomous complex wave solutions are obtained and classified into two c
