量子和经典混沌虽然有密切联系，但是动力学行为却很不相同，甚至截然相反。特别是，在经典混沌中对初始条件的极端敏感性导致系统在动力学演化过程中迅速失去了对初态的记忆; 而完全相反的是，在量子混沌中薛定谔方程的线性本质导致系统可以长时间保持对初态的记忆。不可积量子动力学长期悬而未决的基本问题之一，即是经典混沌如何和各种量子效应相互作用使得系统恢复对初态的记忆。关于这个问题的研究进展不仅有助于理解不可积动力系统中的量子—经典对应等基本概念和实现混沌的量子控制，还有望为近年来凝聚态物理等领域涌现出来的许多混沌现象提供新的洞察。近期，中科院理论物理研究所田矗舜研究员的研究小组和法国里尔大学激光、原子和分子实验室Jean-Claude Garreau教授领导的实验小组合作，解析地预言并用冷原子和量子光学手段验证了量子混沌中的记忆恢复是通过一类奇特的，即由时间驱动的相变来完成的。相关论文发表于Phys. Rev. Lett. 121, 134101 (2018)。
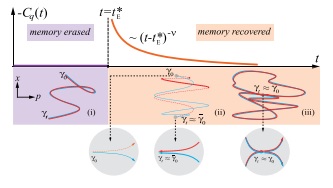
在这个工作的理论部分，作者借助于田矗舜研究员和A. Larkin教授及A. Kamenev教授十多年前发展的弱动力局域化的费曼图理论，对量子混沌的一个代表性模型—量子受激转子的记忆行为进行了解析研究。他们的解析结果表明转子的时间关联函数在一个临界时间，即Ehrenfest时间发生突变：当时间小于该临界时间时关联函数为零，即转子迅速失去对初态的记忆；当时间大于该临界时间时关联函数按幂率衰减，即转子可以长时间保持对初态的记忆，并且幂指数是“普适”的，即只依赖于转子的时间反演对称性是否破缺，而与转子的微观参数无关。作者还进一步证明，时间关联函数和转子的平均转动能量存在一个简单关系，即前者是后者的二阶时间导数；这个关系使得实验上直接研究记忆恢复过程成为可能。这些解析结果表明记忆行为的恢复是通过一个突变—由时间驱动的奇特相变—来完成的。在这个相变中，时间相当于热力学相变中的温度，Ehrenfest时间相当于临界温度，幂指数相当于临界指数，而转子的平均转动能量相当于自由能。
在这个工作的实验部分，作者用原子光学手段实现了量子受激转子模型，包括两个步骤：首先把大约10⁶个铯原子组成的原子云装在磁光约束中并冷却到几个微开；然后用两束具有相同波长的、反向传播的激光脉冲形成驻波，通过和原子发生相互作用，形成激励原子运动的、脉冲化的空间周期势能。在此基础上，作者通过跟踪原子云动量分布的演化探测了受激转子记忆行为随时间的变化，从而验证了理论结果。
此项研究工作由中科院理论物理所、清华大学和法国里尔大学的理论和实验研究人员共同合作完成，并得到了国家自然科学基金委重点项目“小量子系统的动力学研究”、中科院理论物理前沿重点实验室和国家自然科学基金委理论物理专款“彭桓武理论物理创新研究中心”的支持。
　　
　　论文链接：https://link.aps.org/doi/10.1103/PhysRevLett.121.134101