巡游电子量子临界现象，做为凝聚态物理学关联电子系统的传统难题，反复出现在量子物质科学的诸多研究方向上，对其进行合理的模型设计和正确的理论计算，能够帮助人们理解重费米子材料、铜基和铁基高温超导体、过渡金属氧化物、石墨烯层状结构等体系中普遍出现的反常输运、奇异金属和非费米液体行为。然而，巡游电子量子临界现象是典型的量子多体问题，牵扯到对于无穷多耦合着的量子临界玻色、费米自由度的严格处理，传统的以平均场和微扰论为代表的解析方法无法提供定量甚至是定性正确的结果。故而经过理论凝聚态物理学家数十年的努力，虽然高阶圈图计算和新的重正化群方案以及对于非费米液体行为的猜测一直在向前推进，但是系统临界指数和临界动力学行为等等普适的、严格的结论仍然不存在。

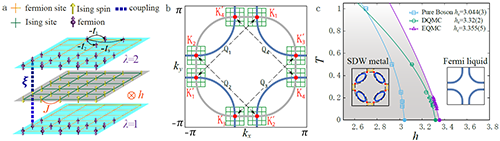
图1: (a) 两层正方晶格费米子耦合反铁磁横场伊辛模型的示意图。(b) 正方晶格上的反铁磁Q =(π, π) 波矢和具有{K, K′} hot spots 的费米面，一对hot spots 被反铁磁涨落波矢Q 联系起来，此处的费米子感受到最强的临界涨落，在临界区中形成了非费米液体。(c) 反铁磁横场伊辛模型(Pure boson)、费米子和反铁磁横场伊辛耦合模型(DQMC, EQMC) 的相图比较。左右的insets 为反铁磁相中形成反铁磁自旋密度波的费米面和顺磁相中无相互作用的费米面的比较。

　　近年来，以新的模型设计和算法突破为代表的大规模量子蒙特卡洛计算取得了长足的进展，为定量研究巡游电子量子临界现象，检验诸多解析猜测的正确性和发展新的理论框架开辟了道路[1, 2, 3]。研究人员通过将无相互作用的费米面与各种玻色子临界涨落耦合起来，成功设计出伊辛向列相、电荷密度波、铁磁和反铁磁自旋密度波以及Z2或者U(1)规范场等等临界涨落与费米子耦合的模型，并且绕过了量子多体系统蒙特卡洛模拟中常见的符号问题，为定量研究众多巡游量子临界系统打开了数值的可能性(这方面的综述文章见[3])。同时，物理认识上的进步也在推动蒙特卡洛计算技术上的进展，尤其以自学习蒙特卡洛(Self-learning Monte Carlo) [4, 5] 和鸸鹋蒙特卡洛(Elective-momentum ultrasize (EMUS) Monte Carlo) 为例[2]，新的蒙特卡洛更新方法降低了传统的费米子行列式蒙特卡洛(Determinantal quantum Monte Carlo, DQMC) 计算复杂度，使得更大尺寸和更低温度系统的模拟成为可能，让人们得到更加接近热力学极限的标度行为。

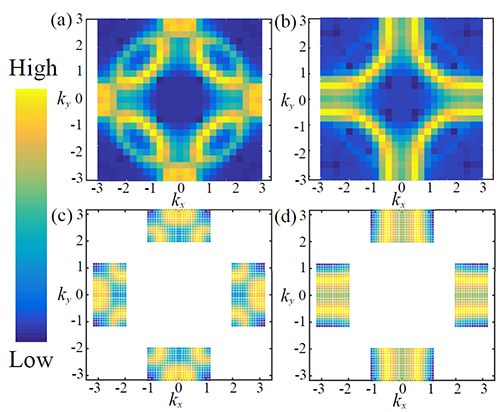图2: (a), (b) 为DQMC 计算得到的费米面。(c),(d) 为EQMC 计算得到的费米面。(a) 和(c) 在反铁磁相(h < hc) 中，能够看到Fermi pocket。(b) 和(d) 为相变点(h = hc) 的结果。可以看到EQMC 计算比DQMC 计算具有更高的动量解析度。

　　具体而言，人们普遍认为，在平均场层面上的Hertz-Millis-Moriya 巡游电子临界行为理论框架，不足以准确描述临界区中的真正标度行为，比如非费米液体的自能和临界玻色传播子的反常标度维度η(anomalous scaling dimension)。但同时，人们也还没有能够在严格的数值计算中证实这样的理论猜测，到目前为止的巡游量子临界点蒙特卡洛模拟结果，受限于模型设计和计算规模，并没有系统地、自洽地观察到超越Hertz-Millis-Moriya 理论的标度行为。这样的情况在日前的一项研究工作中得到了改观[6]，这项研究工作由中国科学院物理研究所/北京凝聚态物理国家研究中心博士生刘子宏、香港科技大学博士后许霄琰、中科院物理所和国科大硕士生潘高培、密歇根大学物理系教授孙锴和中科院物理所研究员/香港大学副教授孟子杨组成的研究团队完成。该团队对于正方晶格反铁磁巡游量子临界点（Q = (π, π)）进行了大尺寸的量子蒙特卡洛数值模拟，由于模型设计和算法的进步，他们第一次确定性地看到了费米面上的hot spots 处的非费米液体行为和临界玻色子的反常标度维度η，为推动理论与数值的结合，建立正确的巡游量子临界理论框架走出了重要一步[6]。为了得到接近热力学极限的量子临界行为，该团队设计了如图1 (a) 所示的晶格模型，其费米子部分的费米面和反铁磁临界玻色子的涨落波矢(Q) 如图1 (b) 所示，整个系统很好地再现了铜基超导体的Néel 反铁磁涨落的模式。在临界区中，费米面上被反铁磁波矢连接的点称为hot spots({K, K′}), 这里的费米子感受到了最强的临界涨落，同时费米子之间的有效相互作用也反馈给了玻色子，将玻色子的临界行为从纯粹的横场伊辛变成了新的普适类，具有了反常标度维度η。在如图1 (c) 所示的相图中，可以清楚地看到反铁磁相变点和从反铁磁金属到顺磁金属的相边界。
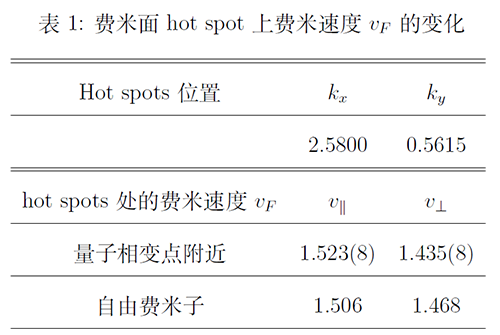
　　该团队采用行列式蒙特卡洛(DQMC) 以及鸸鹋蒙特卡洛(EMUS-QMC, EQMC)，辅以自学习蒙卡的更新方法，计算了到目前为止最大规模的相互作用费米子晶格尺度，并与常规的DQMC 计算进行了系统地比较。常规DQMC能够计算到28×28×200（L×L×L_τ）的规模，而EQMC来研究更大的尺寸：60 × 60 × 320，这样的有限尺寸效应影响更小。通过对于量子临界区以及其标度行为的精确研究，他们发现临界区中的玻色子传播子中具有一个很大的反常维数η~0.125 (如图3所示)，与Hertz-Millis 理论所预言(η~0) 有着显著的差别，但是与高阶圈图计算还有重正化群理论猜测定性吻合。同时，他们还观察到了重正化群计算中预言的，费米面在hot spots 附近由于临界玻色涨落所引入的有效相互作用所造成的费米速度向着反铁磁波矢方向的旋转(如表1所示)。数值与理论的比较对照的结果，弥补了领域中的空白，为成功建立巡游电子量子临界问题的理论框架，提供了严格的素材。

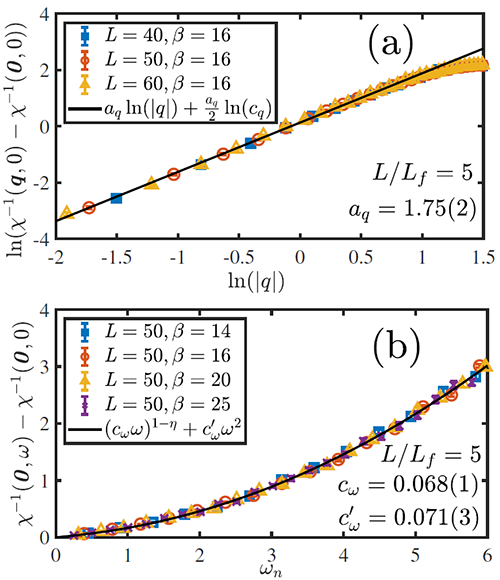图3: (a) 玻色磁化率（传播子）χ(T = 0,h = hc,q,ω)在反铁磁临界点处关于动量|q|的依赖关系，能够从中观察到反常维数χ-1 (q)~|q|2(1-η)，其中η=0.125。(b) 同样的可以看到χ(T = 0,h = hc,q,ω)关于频率ω的依赖关系。小ω时能够看到反常维数χ-1 (ω)~ω1-η,这是系统低能下的超越Hertz-Millis平均场的新行为；大ω时能够看到χ-1 (ω)~ω2的形式，这是系统在高能端和平均场理论吻合的表现。

　　在巡游电子量子临界行为研究的领域，数值计算的进步正在和理论图像上的理解更加紧密地联系起来。有理由相信，许多过去无法严格检验的理论推测，比如非费米液体的能量-动量依赖关系、临界玻色传播子的标度行为，已经可以逐步地、系统地在数值计算中等到检验。同样地，更加正确的理论图像也在指导着更加高效的数值算法和模型设计，使得更大晶格更低温度的计算成为可能。通过数值和理论的良性互动，超越Hertz-Millis-Moriya 理论框架，超越朗道费米液体理论的量子物质科学新范式，正在逐步地建立起来。
　　相关工作[6] 发表在最近一期的《美国科学院学报》（Proceedings of the National Academy of Sciences, PNAS），链接：https://www.pnas.org/content/early/2019/07/31/1901751116
这项工作得到了科技部重点研发计划2016YFA0300502，中科院先导专项XDB28000000，国家自然科学基金委项目11421092, 11574359, 11674370，以及香港特别行政区研究资助局Grant C6026-16W，美国National Science Foundation Grant EFRI-1741618 和Alfred P. Solan Foundation 等机构的支持。研究所进行的大规模并行计算，在中科院物理所量子模拟科学中心，国家超级计算天津中心的天河一号平台，国家超级计算广州中心天河二号平台上进行。研究团队特别感谢国家超算天津中心应用研发部孟祥飞部长、菅晓东工程师，国家超算广州中心应用推广部王栋部长、崔颖妍工程师等人的有力支持和配合。
参考文献：
Xiao Yan Xu, Kai Sun, Yoni Schattner, Erez Berg, and Zi Yang Meng. Non-fermi liquid at (2 + 1)D ferromagnetic quantum critical point. Phys. Rev. X, 7:031058, Sep 2017.doi:10.1103/PhysRevX.7.031058.URL https://link.aps.org/doi/10.1103/PhysRevX.7.031058 .
Zi Hong Liu, Xiao Yan Xu, Yang Qi, Kai Sun, and Zi Yang Meng. Elective-momentum ultrasize quantum monte carlo method. Phys. Rev. B, 99:085114, Feb 2019. doi: 10.1103/PhysRevB.99.085114. URL https://link.aps.org/doi/10.1103/PhysRevB.99.085114 .
Xiao Yan Xu, Zi Hong Liu, Gaopei Pan, Yang Qi, Kai Sun, and Zi Yang Meng. Revealing Fermionic Quantum Criticality from New Monte Carlo Techniques. arXiv e-prints,art. arXiv:1904.07355,Apr 2019.
Junwei Liu, Yang Qi, Zi Yang Meng, and Liang Fu. Self-learning monte carlo method. Phys. Rev.B, 95:041101, Jan 2017. doi:10.1103/PhysRevB.95.041101. URL https://link.aps.org/doi/10.1103/PhysRevB.95.041101 .
Xiao Yan Xu, Yang Qi, Junwei Liu, Liang Fu, and Zi Yang Meng. Self-learning quantum monte carlo method in interacting fermion systems. Phys. Rev. B, 96:041119, Jul 2017. doi: 10.1103/ PhysRevB.96.041119. URL https://link.aps.org/doi/10.1103/PhysRevB.96.041119 .
Zi Hong Liu, Gaopei Pan, Xiao Yan Xu, Kai Sun, and Zi Yang Meng. Itinerant quantum critical point with fermion pockets and hotspots. Proceedings of the National Academy of Sciences, 2019.ISSN 0027-8424. doi: 10.1073/pnas.1901751116. URL https://www.pnas.org/content/early/2019/07/31/1901751116 .

PNAS.1901751116.full.pdf