Marzhan Nassurlla ^1,2,
, N. Burtebayev ^1,3,
, T. Kh. Sadykov ^2,,
, I. Boztosun ^4,
, N. Amangeldi ^1,5,
, D. Alimov ^1,3,
, Zh. Kerimkulov ^1,
, J. Burtebayeva ^1,
, Maulen Nassurlla ^1,3,
, A. Kurakhmedov ^1,5,
, S.B. Sakuta ^6,
, Mesut Karakoc ^4,
, Awad A. Ibraheem ^7,8,,
, K.W. Kemper ^9,
, Sh. Hamada ^10,
,

Corresponding author: T. Kh. Sadykov, turlan43@mail.ru

Corresponding author: Awad A. Ibraheem, awad_ah_eb@hotmail.com

1.Institute of Nuclear Physics, Almaty, Kazakhstan
2.Satbayev University, Institute of physics and technology, 050032, Almaty, Kazakhstan
3.Al-Farabi Kazakh National University, Almaty, Kazakhstan
4.Department of Physics, Akdeniz University, Antalya, Turkey
5.L.N. Gumilyov Eurasian National University, Astana, Kazakhstan
6.National Research Center “Kurchatov Institute”, Moscow, Russia
7.Physics Department, King Khalid University, Abha, Saudi Arabia
8.Physics Department, Al-Azhar University, Assiut Branch, Assiut 71524, Egypt
9.Department of Physics, Florida State University, Tallahassee, Florida 32306, USA
10.Faculty of Science, Tanta University, Tanta, Egypt
Received Date:2020-03-16
Accepted Date:2020-05-30
Available Online:2020-10-01
Abstract:The angular distributions of elastic scattering of ¹⁴N ions on ¹⁰B targets have been measured at incident beam energies of 21.0 and 24.5 MeV. Angular distributions at higher energies 38–94.0 MeV (previously measured) were also included in the analysis. All data were analyzed within the framework of the optical model and the distorted waves Born approximation method. The observed rise in cross sections at large angles was interpreted as a possible contribution of the α-cluster exchange mechanism. Spectroscopic amplitudes SA₂ and SA₄ for the configuration ¹⁴N→ ¹⁰B +α were extracted. Their average values are 0.58±0.10 and 0.81±0.12 for SA₂ and SA₄, respectively, suggesting that the exchange mechanism is a major component of the elastic scattering for this system. The energy dependence of the depths for the real and imaginary potentials was found.

HTML

--> --> -->

In elastic scattering between p- and sd-shell nuclei, a considerable increase in the differential cross sections at large angles is often observed. This effect, often called anomalous large-angle scattering (ALAS), is particularly observed in the interaction of nuclei with a pronounced α-cluster structure. Such an increase in the cross sections cannot be reproduced within the framework of an optical model with reasonable potential. In a number of works [1-7], the description of ALAS is achieved by including a contribution from the transfer mechanism of nucleon(s) added to the elastic scattering. This addition has led to a significant improvement in the description of the differential cross sections of the elastic scattering in the full angular range obtained in the framework of the coupled reaction channels (CRC) and distorted waves Born approximation (DWBA) methods. This phenomenon has so far been observed in the elastic scattering and reactions between 1p-shell nuclei that differ in mass by one, two, and even three nucleons in addition to that of the α particle.
There are extensive previously published elastic transfer studies including ¹⁴N(¹⁰B,¹⁴N)¹⁰B. The elastic scattering for the ¹⁴N+¹⁰B system was measured at the energies of 38.1–50.0 MeV [2], 73.9 MeV, and 93.6 MeV [8]. In Ref. [8] the angular distributions of ¹⁴N elastically scattered by ¹⁰B were measured in the limited angular range of up to 50° in the center of the mass system. In Ref. [2], measurements of angular distributions were extended to large angles (~ 150°) where a significant rise was exhibited. This rise was reproduced by taking into consideration the effect of α-cluster transfer.
In the present work, elastic scattering in the ¹⁴N + ¹⁰B system was measured at E_lab = 21.0 and 24.5 MeV in order to verify the role of α-cluster transfer between ¹⁴N and ¹⁰B at energies closer to the Coulomb barrier. The interest in such a study is because the number of reaction channels in the scattering decreases rapidly around the Coulomb barrier. The available data [2, 8] for the ¹⁴N+¹⁰B system were also reanalyzed using both the optical model (OM) and the DWBA method to obtain an energy-dependent potential that could fairly reproduce the elastic scattering data in the full angular range by taking into account the contribution of the α-transfer mechanism.
This work complements the ongoing program for studying elastic scattering at low energies at the DC-60 cyclotron [5, 9], in which scattering in the collision of light heavy ions is studied to take into account the possible contribution of the particle exchange mechanism. The paper is organized as follows. In Section 2, the measurement procedure of ¹⁴N +¹⁰B angular distribution is described. Section 3 is devoted to theoretical analysis, results, and discussion. A summary is given in Section 4.

The differential cross sections for elastic scattering of ¹⁴N ions on ¹⁰B nucleus were measured at the DC-60 cyclotron of Institute of Nuclear Physics (Astana, Kazakhstan). ¹⁴N ions were accelerated up to energies of 21.0 and 24.5 MeV and then impinged on a self-supported ¹⁰B (with 90% enrichment) target with a thickness of 30 μg/cm². The target was located in the center of the scattering chamber with diameter of 43 cm. Reaction products were recorded with one telescope consisting of two silicon detectors (?E-Е). ?Е is a surface barrier detector with a thickness of 10 μm, and E is the complete absorption detector with a thickness of 200 μm. The measurements were performed in the angular range of 31°–153° with an increment of 2° in the center of mass system. A Faraday cup was used to integrate the total incident currents on the target. The ΔE-E spectrum of the reaction products and typical energy spectra of ¹⁴N are shown in Fig. 1. In Fig. 1(a), the ΔE-E spectrum demonstrates excellent Z separation between reaction products (B, C, and N). The energy resolution was about 500 keV and was mainly determined by the energy spread in the cyclotron beam and the target thickness. Such resolution allowed for a clear identification of the several peaks in the spectrum. A typical energy spectrum of ¹⁴N scattered by ¹⁰B is shown in Fig. 1(b).
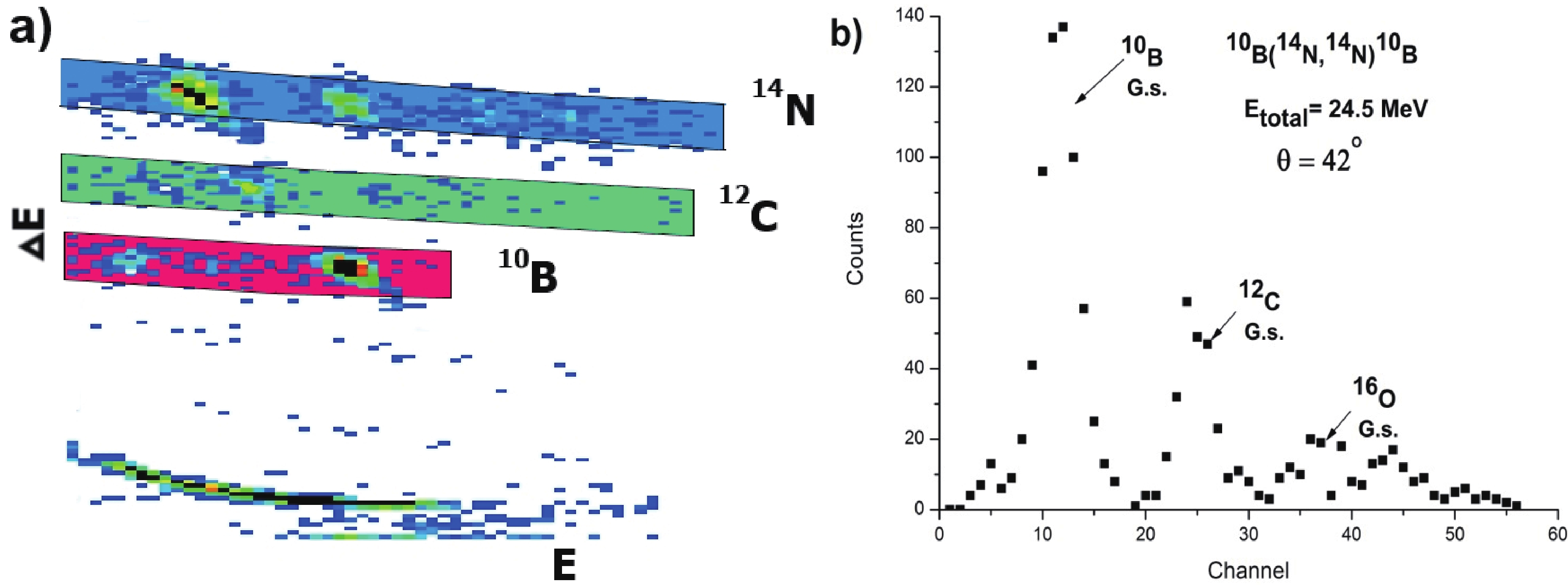Figure1. (color online) (a) ΔE-E spectrum of the reaction products for the ¹⁴N+¹⁰B system. (b) The energy spectrum of ¹⁴N scattered by the ¹⁰B target at the beam energy of 24.5 MeV measured at an angle θ= 42°.

The angular distributions of elastic scattering of ¹⁴N on ¹⁰B nucleus at the energies of 21.0 MeV and 24.5 MeV are shown in Fig. 2. These distributions were normalized to OM cross sections at small angles, where it is relatively independent of the parameters of the nuclear potential. The normalization error was smaller than 10%. As can be seen from Fig. 2, in the front hemisphere, a smooth decrease in the cross sections is observed without a pronounced oscillation structure. With a further increase in the angles, the decrease stops and a weakly expressed diffraction structure appears with cross sections rising at angles greater than 120°. We estimated the systematic error of measured cross sections to be no larger than 10%. The statistical error was 1%–5% during our measurements in the forward hemisphere region. It increased at large angles, but nowhere did it exceed 10%. The error bars in Fig. 2 are smaller than the size of the experimental points.
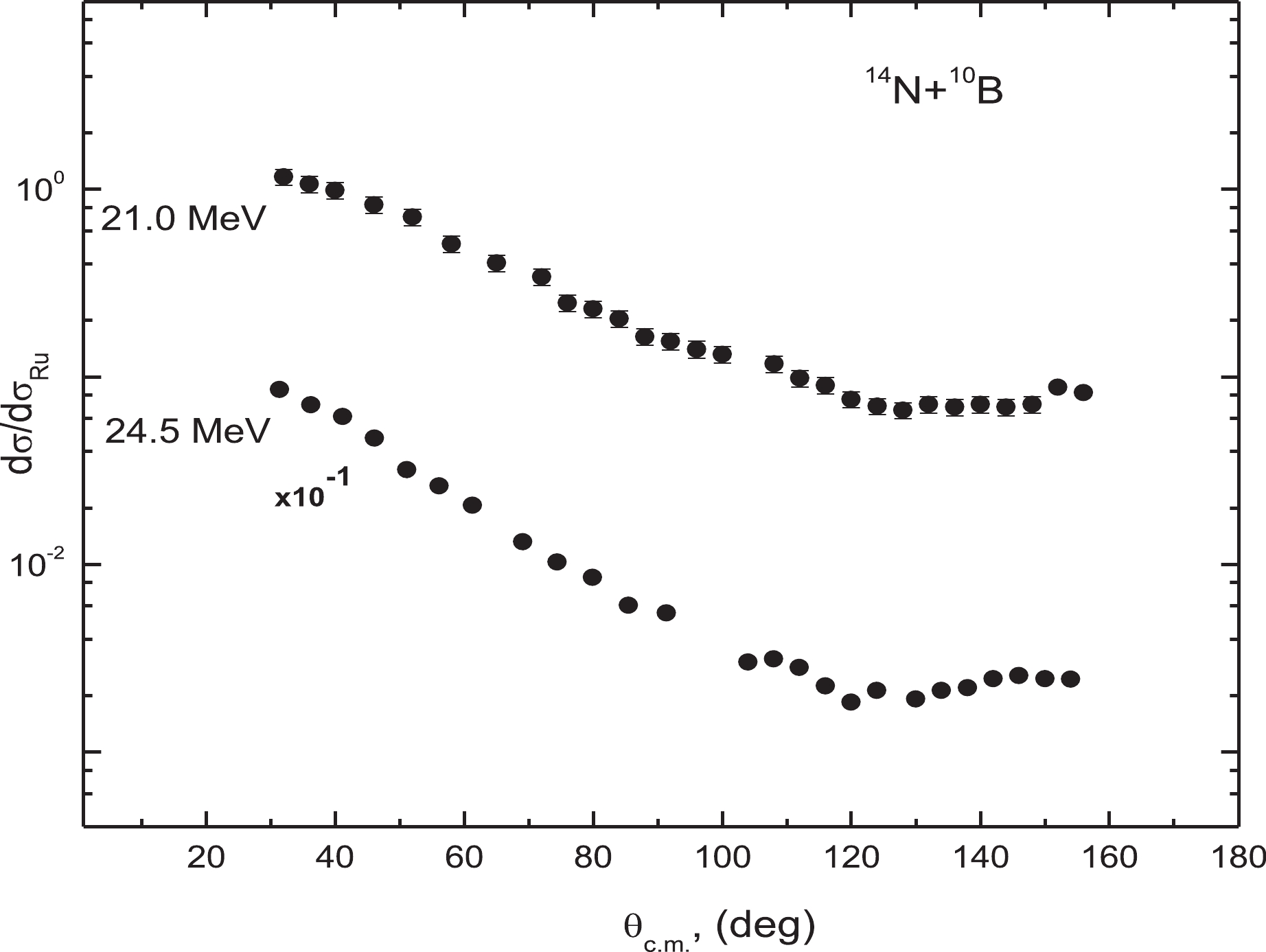Figure2. Experimental angular distributions of elastic scattering of ¹⁴N by ¹⁰B nuclei at the beam energies of 21.0 MeV and 24.5 MeV.

It is well known that the extracted values for spectroscopic amplitudes from scattering and transfer reactions are highly dependent on the potential parameters used in the various analyses. Based on this fact, the experimental data for the ¹⁴N+¹⁰B nuclear system were first analyzed under the assumption of pure potential scattering. In this case, the differential cross sections were calculated in the framework of the phenomenological optical model and the interaction potential was found by fitting the calculated cross sections to the experimental data. The considered total potential is the sum of three terms: a) ${V_C}(R)$: Coulomb potential of a uniform charged sphere with radius parameter fixed at 1.3 fm; b) real volume part; and c) an imaginary volume part of nuclear potential with both Woods-Saxon shapes. Thus, the total potential has the following shape:

$\begin{split} U{\rm{(}}R{\rm{)}} =& {V_C}(R) - {\rm{ }}{V_0}{\left[ {1 + \exp \left( {\frac{{r - {R_V}}}{{{a_V}}}} \right)} \right]^{ - 1}} \\&- {\rm i}{W_0}{\left[ {1 + \exp \left( {\frac{{r - {R_W}}}{{{a_W}}}} \right)} \right]^{ - 1}}, \end{split}$

(1)

where V₀, a_V and W₀, a_W are the depths and diffusenesses of the real and imaginary parts of the nuclear potential, respectively. Radii in these expressions are defined as ${{R}_{V,W,C}}={{r}_{V,W,C}}{\rm{ x }}\left( {\rm{A}}_{\rm{p}}^{{}^{\rm{1}}\!\!\diagup\!\!{}_{3}\;}+{\rm{A}}_{\rm{t}}^{{}^{\rm{1}}\!\!\diagup\!\!{}_{3}\;} \right)$. In addition to our measurements for ¹⁴N+¹⁰B elastic scattering angular distributions at E_lab=21.0 and 24.5 MeV, we also reanalyzed data at all the available energies: at E_lab=38.1, 42.0, 46.0, and 50.0 MeV, taken from Ref. [2], and at E_lab= 73.92 and 93.6 MeV, taken from Ref. [8], in order to obtain energy-dependent potential parameters for this nuclear system. We performed OM calculations using starting parameters taken from Ref. [8], and only the three parameters V₀, W₀, and a_W were varied and the other three, r_V, r_W, and a_V, were fixed at 0.92, 1.29, and 0.77 fm, respectively.
Angular distributions at energies of 24.5–50.0 MeV showed a significant increase in differential cross sections at backward angles, which was assumed to arise from the contribution of α-cluster transfer between ¹⁴N and ¹⁰B. The experimental data at 21.0 MeV, which is closer to the Coulomb barrier energy for the ¹⁴N+¹⁰B nuclear system, only showed a slight increase in cross sections at backward angles. However, a rise is already observed at energy 24.5 MeV, confirming that the transfer phenomenon is highly dependent on the projectile’s energy. The angular distributions at the two higher energies 73.92 and 93.6 MeV were measured in a limited angular range and did not extend beyond ~ 50°, and thus, the transfer phenomenon is not presented.
As mentioned above, experimental data in the energy range 21–50 MeV showed a significant increase in cross sections at backward angles, except at E_lab=21.0 MeV, which showed a slight increase. Such increase in cross sections could not be reproduced by the simple OM, and its origin was investigated in terms of α-cluster transfer implemented through the distorted waves Born approximation (DWBA) method. As the ground state spin-parity of ¹⁴N is J^π=1⁺, an alpha particle coupled to a ¹⁰B core with J^π=3⁺ can be found in two differential orbitals with angular momentum L=2 or L=4. The configuration with the higher angular momentum should be favored as the cluster configuration with L=4 has a theoretical spectroscopic factor much larger than that of the one with L=2 (SA₂=0.11 and SA₄=0.83) [10]. However, two possible configurations have been taken into account. The experimental angular distributions at the different energies were analyzed up to angles 90° by the optical model to exclude the effect of cluster transfer and other effects that could affect the cross sections at backward angles using the FRESCO code [11]. The comparisons between the experimental angular distributions in the energy range 21–93.6 MeV and theoretical calculations using both OM and DWBA, incorporated in the Coupled Reactions Channels program (FRESCO) [11], are shown in Figs. 3-5 with the potential parameters listed in Table 1.

E/MeV	Model	V0/MeV	W0/MeV	aW/fm	χ2/N	SA	σR/mb
21.0	OM	98.02±5.0	14.39±0.7	0.39	0.18		623.4±30
	DWBA – L=2				0.21	0.69±0.04
	DWBA – L=4				0.47	0.93±0.04
24.5	OM	99.33±5.0	14.51±0.7	0.44	0.57		789.4±39
	DWBA – L=2				1.25	0.42±0.04
	DWBA – L=4				2.4	0.77±0.04
38.1	OM	87.24±4.3	17.0±0.8	0.45	5.8		1121±56
	DWBA – L=2				18.6	0.61±0.033
	DWBA – L=4				7.9	0.8±0.033
42.0	OM	86.8±4.3	18.0±0.9	0.476	6.54		1198±60
	DWBA – L=2				42.2	0.62±0.02
	DWBA – L=4				23.6	0.78±0.02
46.0	OM	84.35±4.2	22.0±1.1	0.402	4.3		1173±60
	DWBA – L=2				14.3	0.59± 0.03
	DWBA – L=4				6.7	0.76± 0.03
50.0	OM	83.15±4.2	23.0±1.2	0.393	9.3		1197±60
	DWBA – L=2				17.5	0.56±0.03
	DWBA – L=4				15.5	0.81±0.03
73.9	OM	76±3.8	28.0±1.4	0.373	4.3		1288±60
93.6	OM	64±3.2	33.0±1.6	0.358	11.3		1313±60

Table1.Optical potential parameters for the ¹⁴N+¹⁰B system at different energies, together with spectroscopic amplitudes extracted from the DWBA analysis. Note that χ²/N values (normalized per number of experimental points) refer to θ_c.m.<90° for the elastic scattering and the full angular range for the DWBA calculations. The parametersr_V, r_W, and a_V were fixed at 0.92, 1.29, and 0.77 fm, respectively.

Figure3. (color online) Comparison between the experimental data (black circles) and calculations for the ¹⁰B(¹⁴N,¹⁴N)¹⁰B elastic scattering at E_lab= 21.0, 24.5, and 38.1 MeV. The dashed black curves denote pure optical model fits to the data for angles θ_c.m.< 90?. The dashed red and solid blue curves denote the results of calculations taking into account the process of elastic transfer of the α-particle in the¹⁰B(¹⁴N,¹⁰B)¹⁴N reaction to L= 2 and L= 4 orbitals, respectively.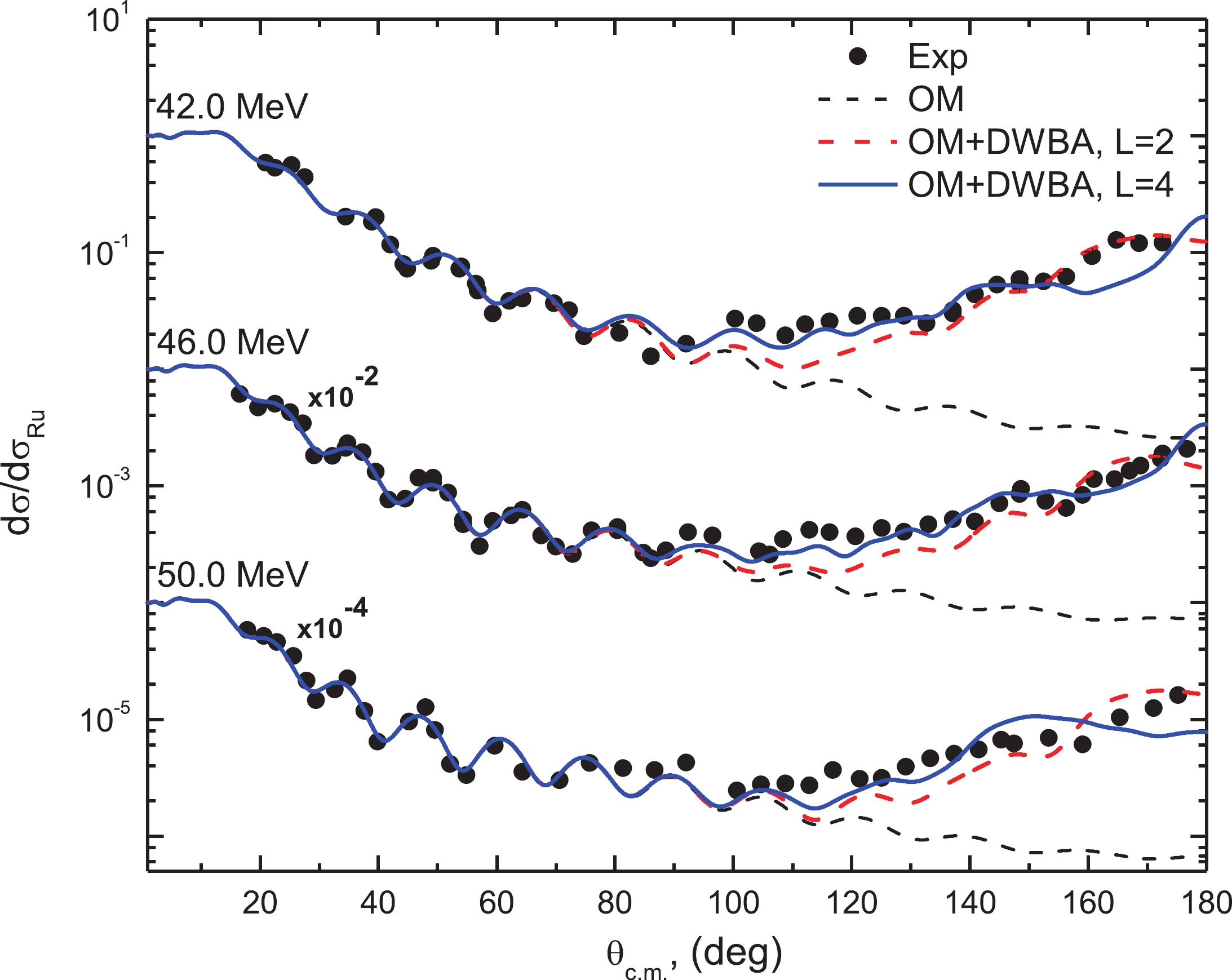

Figure4. (color online) Same as Fig. 3 but at energies 42.0, 46.0, and 50.0 MeV.

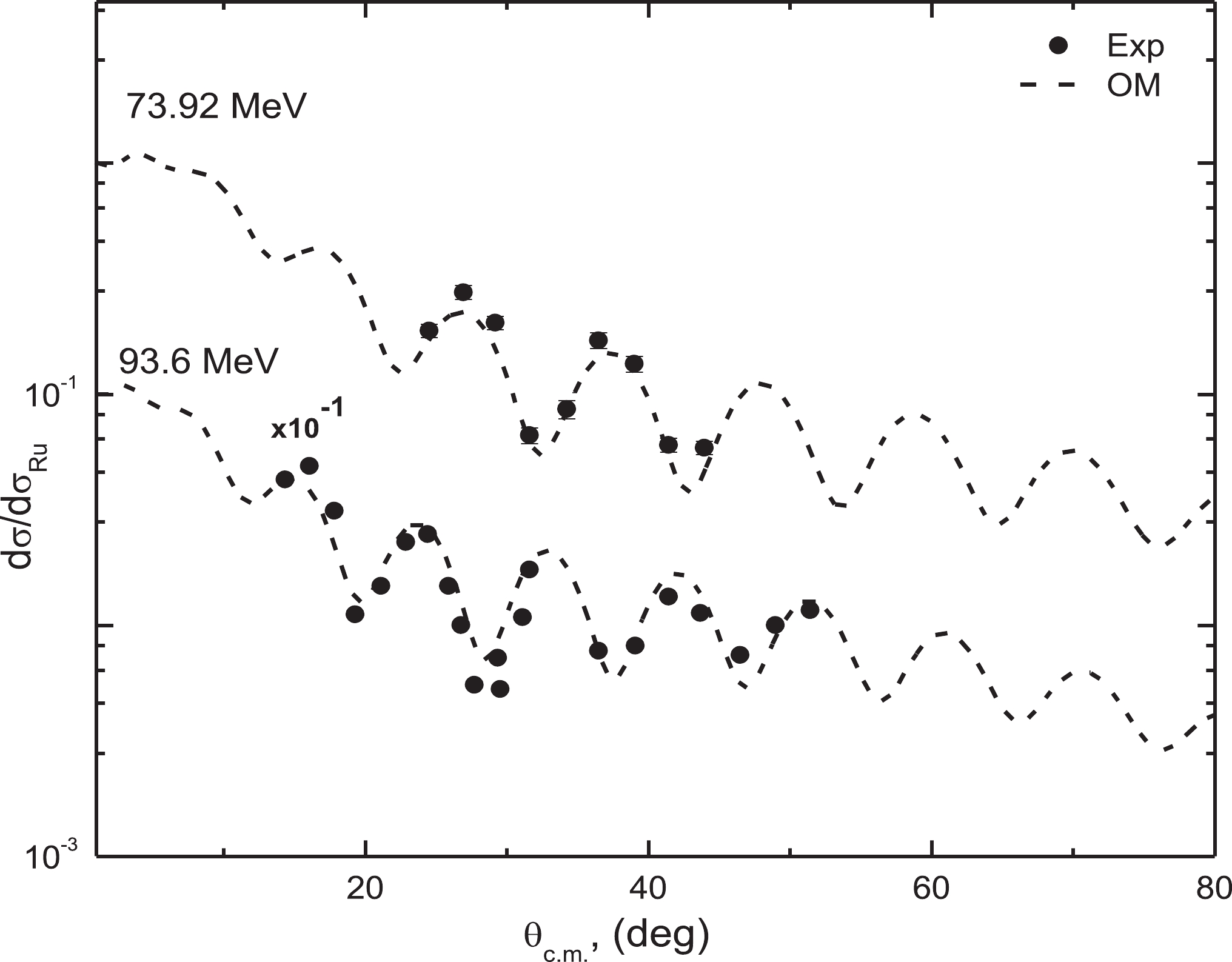Figure5. Comparison between experimental angular distributions for ¹⁰B(¹⁴N,¹⁴N)¹⁰B elastic scattering at E_lab= 73.92 and 93.6 MeV (black circles) and the theoretical calculations (dashed curves) using OM.

The significant increase in differential cross sections at large angles can be explained as arising from α-cluster transfer as shown by DWBA calculations that were performed to explore this possibility. In this case, the exchange of the α-cluster between the two interacting nuclei ¹⁴N, to be treated as (¹⁰B – Core) + (α-particle – valence), leads to an exit channel that is physically indistinguishable from the entrance channel. Therefore, the differential cross section is the square of the sum of amplitudes from the pure elastic scattering and the exchange mechanism of the cluster transfer, as follows [12, 13]:

$ \frac{{{\rm d}{\sigma _{el}}}}{{{\rm d}\Omega }} = {\left| {{f_{el}}\left( \theta \right) + {{\rm e}^{{\rm i}\alpha }}S{f_{\rm DWBA}}\left( {\pi - \theta } \right)} \right|^2}, $

(2)

where ${f_{el}}(\theta )$ is the elastic scattering amplitude, ${f_{\rm DWBA}}(\pi - \theta )$ is the amplitude calculated using the distorted wave method with the replacement $\theta \to \pi - \theta $, parameter α = pi (coherence of amplitudes), and S is the product of the two spectroscopic amplitudes (SA) of the transferred particle in the entrance and exit channels, which are the same in the case of elastic transfer.
Calculations of transfer are performed using the optical potential parameters obtained from fitting the data in the forward hemisphere up to 90°. The bound state wave function for the relative motion of the α-particle and ¹⁰B in the ¹⁴N configuration cluster plus core is defined by a Woods-Saxon potential with fixed radius $R=1.25{\rm{x }} $$\left( 4_{{}}^{{}^{1}\!\!\diagup\!\!{}_{3}\;}+10_{{}}^{{}^{1}\!\!\diagup\!\!{}_{3}\;} \right)$ fm and the diffuseness a = 0.65 fm. The potential depth was adjusted to reproduce the binding energy of the cluster (11.612 MeV). The quantum numbers of the radial motion of the clusters relative to the core were determined from the following expression of the shell model [13, 14]:

$ 2(N - 1) + L = \sum\limits_{i = 1}^n {2({n_i}} - 1) + {l_i}, $

(3)

where N is the number of nodes of the radial wave function of relative motion (taking into account the node at r = 0) and L is the corresponding orbital momentum of the cluster; Σ denotes the sums of similar quantities for nucleons entering a cluster in a bound state. Two different sets for cluster quantum numbers for the overlaps $\left\langle {{{}^{{\rm{14}}}{\rm{N}}}} | {{\alpha { + ^{{\rm{10}}}}{\rm{B}}}} \right\rangle $ are used in our calculations, as listed in Table 2, due to the two possibilities of transfer to L=2 and L=4 orbitals. The same potential parameters are taken for the entrance channel (¹⁴N+¹⁰B) and the exit channel (¹⁰B+¹⁴N). The spectroscopic amplitude was taken as a free parameter that is varied to give the best agreement between the theoretical calculations and the experimental data. The variation of the extracted SA₂ and SA₄ with χ²/N at E_lab= 21–50 MeV is shown in Figs. 6 and 7, respectively. The values of SA₂ and SA₄ at the different energies are listed in Table 1. As can be seen, the average values of SA₂ and SA₄ are 0.58 ± 0.10 and 0.81 ± 0.12, respectively. The obtained SA₂ value overestimates the theoretical value calculated by Kurath [10] in the framework of the shell model, whereas the extracted SA₄ is in good agreement.

Overlap	N(Number of nodes)	L	S	J = L+S	Binding energy/MeV
$\left\langle {{{}^{{\rm{14}}}{\rm{N}}}} / {{^{{\rm{10}}}{\rm{B}} + \alpha }} \right\rangle $	2	2	0	2	11.612
	1	4	0	4

Table2.Cluster quantum numbers for the overlaps used in our calculations.

Figure6. (color online) Variation of χ²/N with extracted SA₂ at E_lab = 21, 24.5, 38.1, 42.0, 46.0, and 50.0 MeV.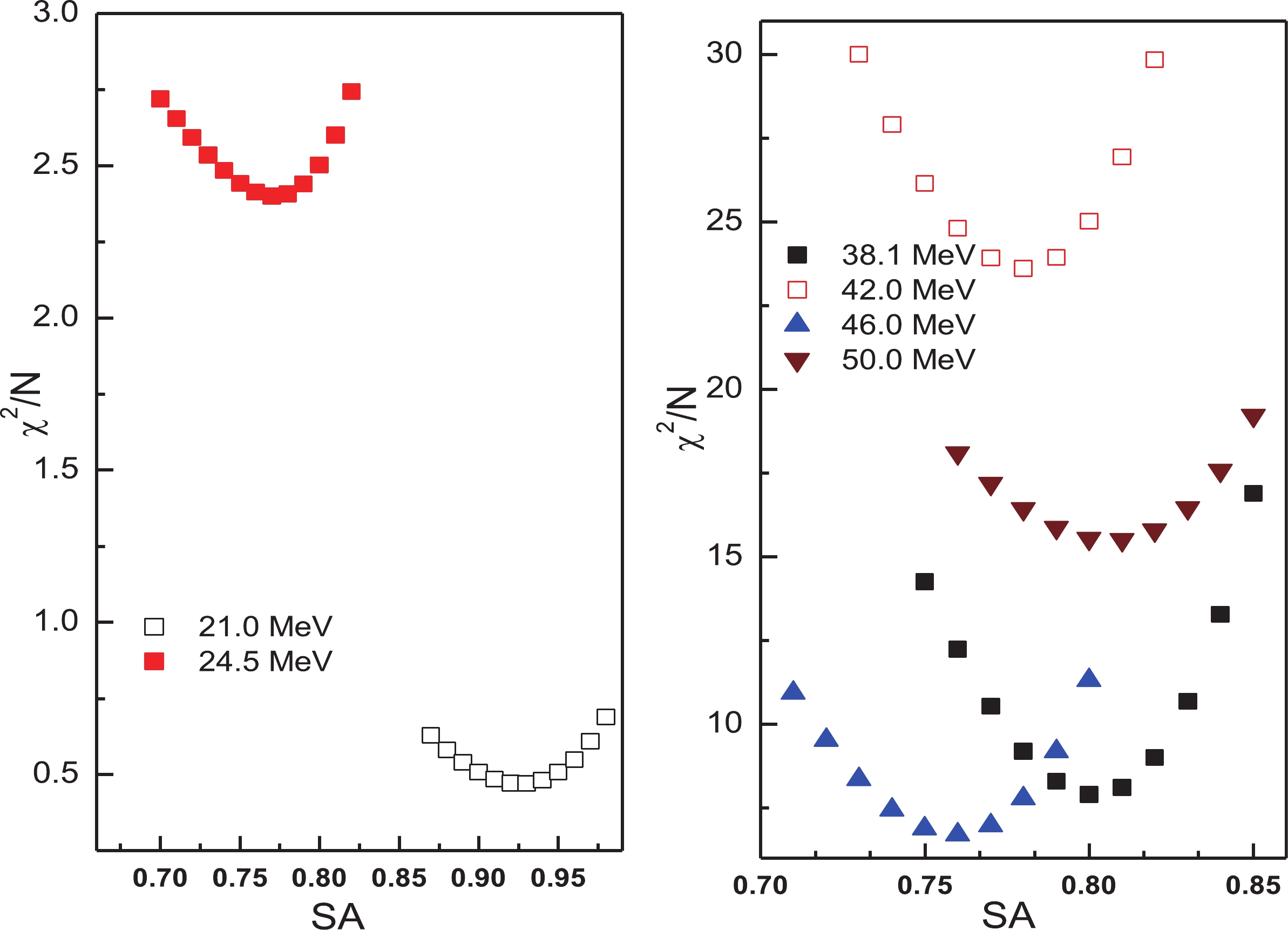

Figure7. (color online) Variation of χ²/N with extracted SA₄ at E_lab= 21, 24.5, 38.1, 42.0, 46.0, and 50.0 MeV.

As can be seen from Figs. 3 and 4 and Table 1, the values of dσ/dσ_RU at the largest angles (dσ/dσ_RU~0.2) and the spectroscopic amplitudes are practically independent of the beam energy. The same result was obtained in Ref. [2].
The contribution of the α-cluster in forming the cross sections at backward angles at E = 46.0 MeV, measured by Takai et al. [2], was analyzed within the framework of the DWBA method by code LOLA [15]. Their and our analyses are compatible at the forward angles region, but there is a significant difference at the backward angles, as shown in Fig. 8. However, in Ref. [2], they did not present χ²/N when comparing both theoretical calculations. However, it is clearly shown in Fig. 8 that the current analysis is much better. Our analysis at 46.0 MeV could reproduce the experimental data well, especially at angles > 160°, whereas in the previous analysis the data and the calculations are completely out of phase at large angles (> 160°). It is noteworthy that the extracted SA₄ at E = 46.0 MeV from the current work (0.76) is so close to the used SA₄ (0.806) in Ref. [2].
Figure8. (color online) Comparison between the experimental angular distribution for ¹⁴N+¹⁰B elastic transfer at large angles region (black circles) and the current DWBA calculations (solid red curves). The dashed black curve displays the results of Ref. [2].

As mentioned before, the investigation of the ¹⁰B(¹⁴N,¹⁰B)¹⁴N α-cluster transfer process to L=2 and L=4 orbitals individually leads to an extracted SA₄ value of “0.81 ± 0.12”, which is close to the theoretical value calculated by Kurath [10], whereas the extracted SA₂ exceeds the theoretical value. Therefore, further calculations were performed to study the ¹⁰B(¹⁴N,¹⁰B)¹⁴N α-cluster transfer process by taking into consideration the transfer to L=2 and L=4 orbitals simultaneously. The potential parameters listed in Table 1 are used in the theoretical calculations. The optimal SA₂ and SA₄ values were searched using the SFRESCO search code [11]. During the search process, SA₂ and SA₄ were allowed to be changed freely in the range 0.05–0.7 and 0.6–0.95, respectively, till the best agreement between experimental data and calculations was reached. The starting parameters for SA₂ and SA₄ are 0.1 and 0.83, respectively; these values are adopted from the work of Kurath [10]. The optimal extracted values for SA₂ and SA_4,as well as the χ² / N values, at different concerned energies using this technique are listed in Table 3. The comparison between the experimental data and the theoretical calculations using this method are shown in Figs. 9 and 10. Although in an elastic transfer process the entrance and exit channels are identical and consequently the same SA should be taken for both channels, in this case the value of SA₂ was used as the spectroscopic amplitude for the entrance channel and the value of SA₄ was used as the spectroscopic amplitude for the exit channel. Thus, the experimental differential cross sections ${\left( {\dfrac{{{\rm d}\sigma }}{{{\rm d}\Omega }}} \right)_{\exp }}$ are assumed to be described as a coherent sum:

E/MeV	SA2	SA4	χ2/N
21.0	0.7±0.11	0.81±0.02	0.26
24.5	0.2±0.04	0.65±0.01	2.3
38.1	0.54±0.01	0.75±0.02	10.9
42.0	0.47±0.01	0.81±0.02	31.7
46.0	0.57±0.01	0.79±0.01	17.3
50.0	0.5±0.01	0.65±0.01	15.4

Table3.Optimal extracted values for SA₂ and SA₄ at the different energies (E), taking into account the contribution from L=2 and L=4 orbitals simultaneously as well as the χ²/N values.

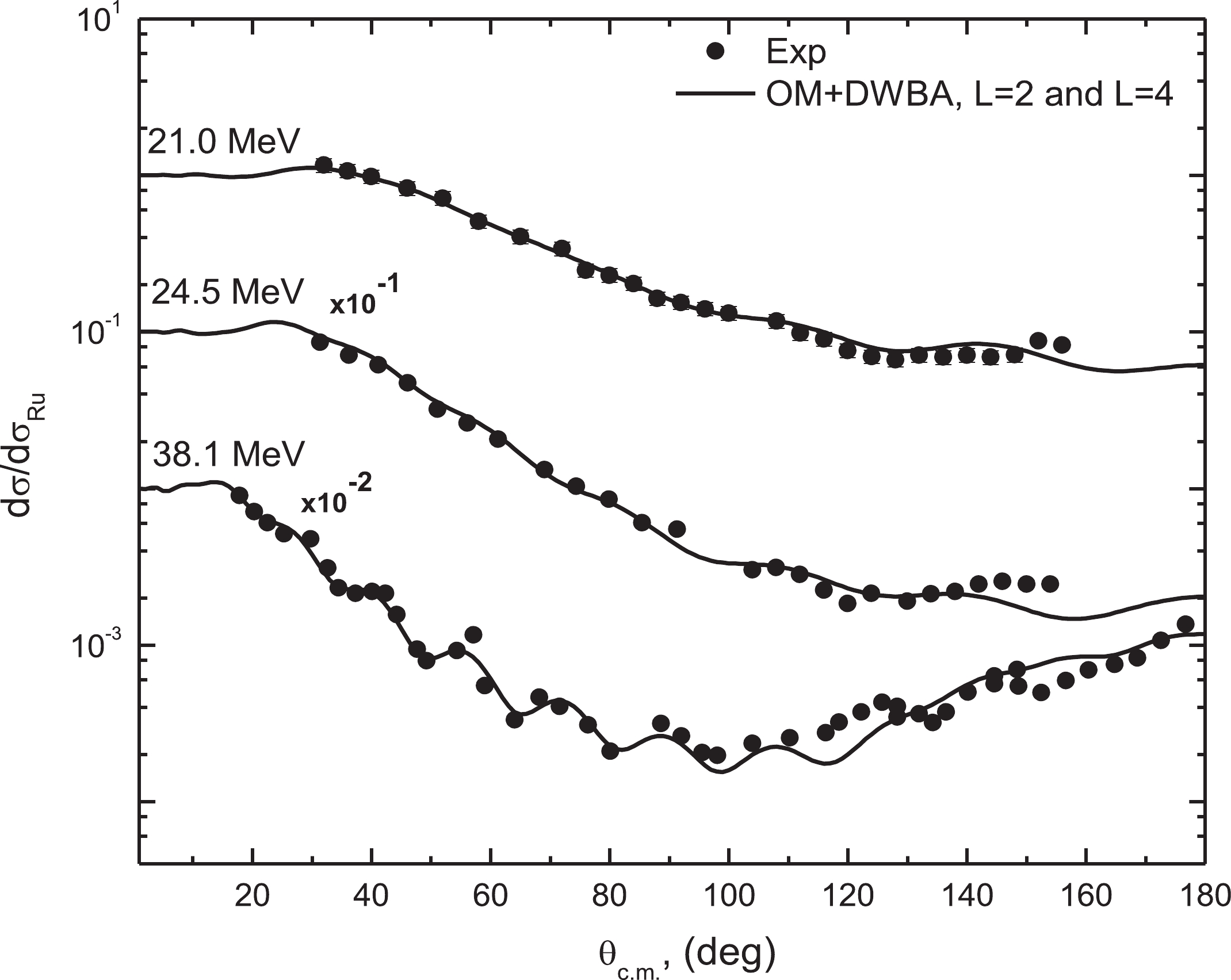Figure9. Comparison between the experimental data (black circles) and DWBA calculations including the ¹⁰B(¹⁴N,¹⁰B)¹⁴N elastic transfer process to L=2 and L=4 orbitals simultaneously at energies 21.0, 24.5, and 38.1 MeV.

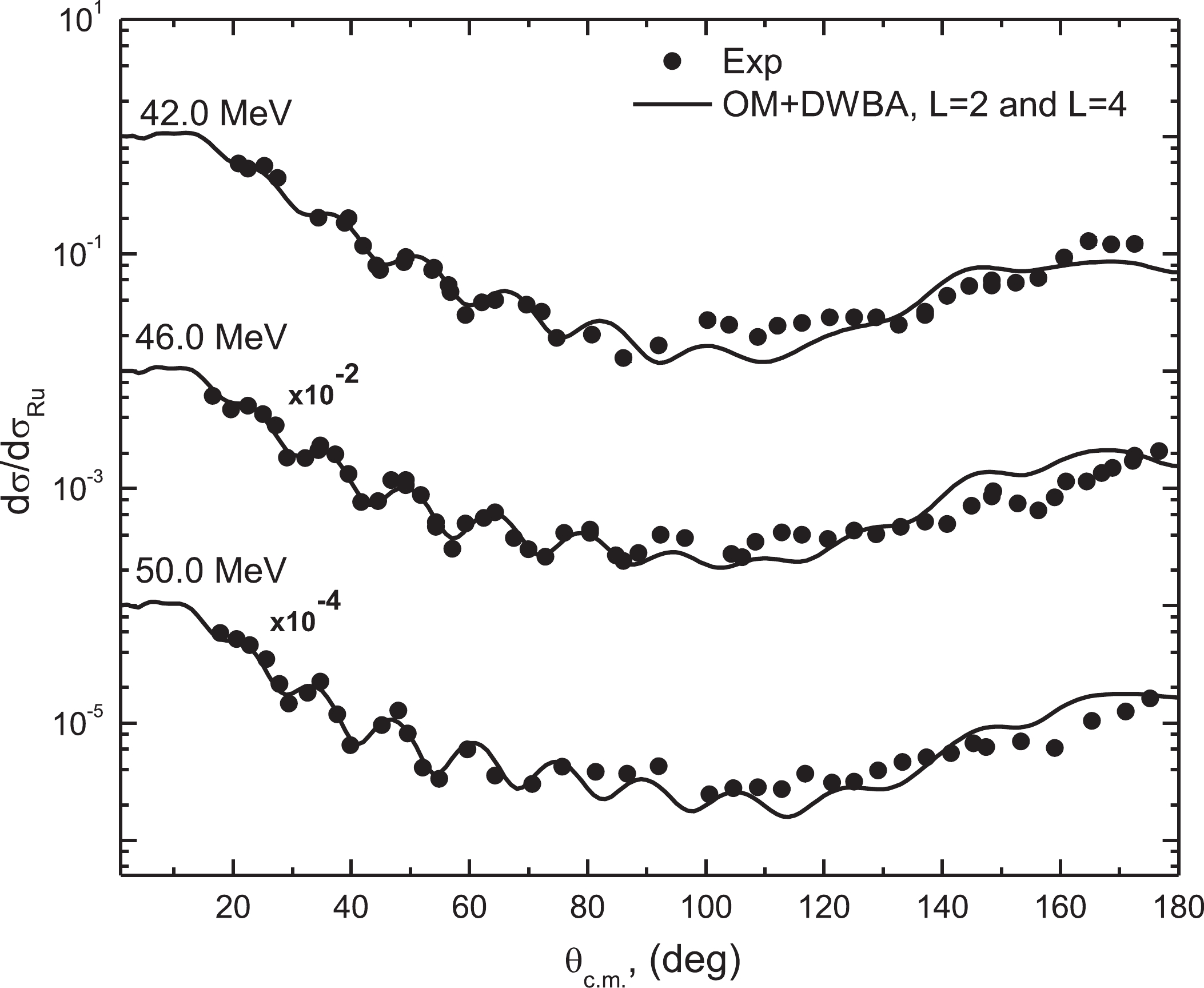Figure10. Same as Fig. 9 but at energies 42.0, 46.0, and 50.0 MeV.

$ {\left( {\frac{{{\rm d}\sigma }}{{{\rm d}\Omega }}} \right)_{{\rm{exp}}}} = {\left( {\frac{{{\rm d}\sigma }}{{{\rm d}\Omega }}} \right)_{{\rm{DWBA (}}L = {\rm{2)}}}} + {\left( {\frac{{{\rm d}\sigma }}{{{\rm d}\Omega }}} \right)_{{\rm{DWBA (}}L = 4{\rm{)}}}}. $

(4)

As mentioned above, in the work of Takai et al. [2], the spectroscopic amplitude close to our value was used to reproduce the experimental angular distributions for ¹⁰B(¹⁴N,¹⁰B)¹⁴N elastic transfer at all the considered energies. Nevertheless, in the work of Motoboyashi [8], the extracted SA was 1.3. This discrepancy between the spectroscopic amplitudes predicted by theory and those deduced by a DWBA analysis was reported early by many authors (see, for example, [16, 17]) and points to the need for further experimental as well as theoretical exploration of scattering the 1p-shell nuclei.
Figure 11 shows the energy dependence of the found by us potentials, which are listed in Table 1. It is seen that a linear function is a fair approximation for the energy dependence for the depths of the real and imaginary parts of the optical potentials in the energy range from 20 to 100 MeV for the ¹⁰B+¹⁴N system. With increasing energy, the depth of the real potential decreases and can be approximated by the formula V₀ = 107.2-0.46E, and the depth of the imaginary potential increases and is well described by the formula W₀ = 8.19+0.268E.
Figure11. (color online) Energy dependence on V₀ and W₀ for the ¹⁰B(¹⁴N, ¹⁴N)¹⁰B system.

An important and useful characteristic of optical potentials is the volume integrals over V(r) and W(r),

$ {J}_{V}=\frac{1}{{A}_{p}{A}_{t}}\int V\left(r\right)4\pi {r}^{2}{\rm d}r \;\;\;\;{\rm{and}}\;\;\;\;{J}_{W}=\frac{1}{{A}_{p}{A}_{t}}\int W\left(r\right)4\pi {r}^{2}{\rm d}r. $

(5)

where A_p and A_t denote the masses of projectile (p) and target nucleus (t), respectively.
The volume integrals corresponding to the found potentials, as well as the depths, smoothly vary depending on the energy within 200–300 MeV fm³ for J_V and 70–210 MeV fm³ for J_W. This is consistent with similar dependencies known from the scattering of p + ¹²С, ³He + ¹²С, α + ¹²С, and ¹²С + ¹²С [18-20]. Our potentials are physically reasonable, as their volume integrals (J_V) are close to that calculated by microscopic models [18].
The energy dependence of the total reaction cross sections σ_R obtained in this work is presented in Fig. 12. It can be seen that the rapid growth of cross sections at energies in the range of 20–40 MeV is replaced by a slower one at Е greater than 50 MeV.
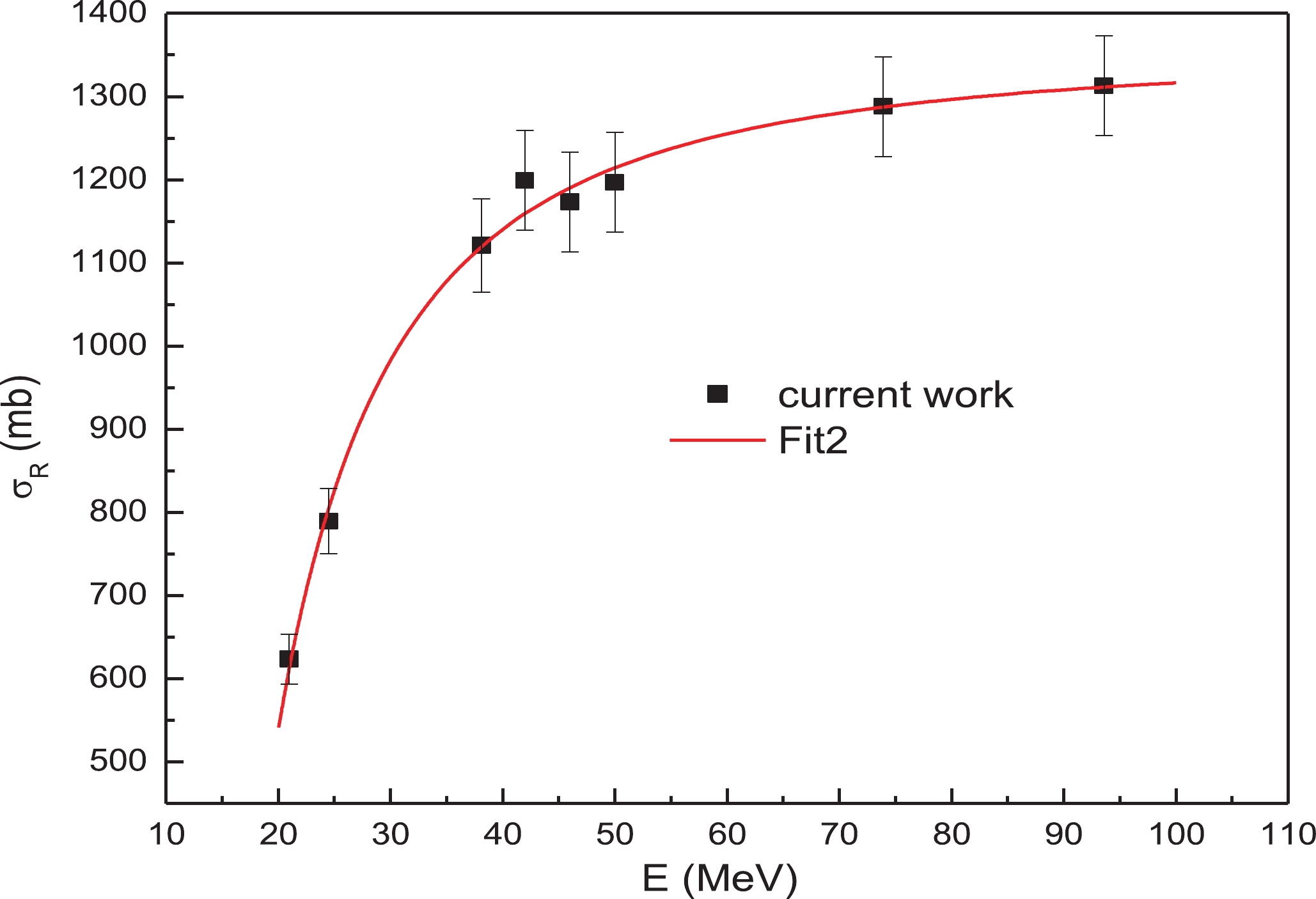Figure12. (color online) Energy dependence of the extracted total reaction cross sections for the ¹⁰B(¹⁴N, ¹⁴N)¹⁰B elastic scattering from the current work.

It is well known that the total reaction cross section calculated in the framework of the optical model is practically independent of the details of the real part of the optical potential and is mainly determined by the parameters of its imaginary part, the depth of which, as can be seen from Table 1, increases from 14 to 33 MeV with increasing energy up to 93 MeV. The calculated energy dependence of the total cross sections is adequately approximated by the expression:

${{\sigma }_{R}}(E)=1.3 \pi {{\left( A_{P}^{{}^{1}\!\!\diagup\!\!{}_{3}\;}+A_{T}^{{}^{1}\!\!\diagup\!\!{}_{3}\;} \right)}^{2}}\left( 15.97-\frac{12.25}{E}-\frac{3595.1}{{{E}^{2}}} \right).$

(6)

Angular distributions for ¹⁴N+¹⁰B elastic scattering were investigated at energies of E_lab(¹⁴N) = 21.0 and 24.5 MeV. The measured data obtained at these energies, which are closer to the Coulomb barrier, showed a smooth, structureless decrease in the cross sections in the region of the angles of the forward hemisphere with a slight increase at large angles. Further, data at higher energies 38.1–50.0 MeV showed a Fraunhofer diffraction pattern at forward angles with a remarkable rise in cross sections at backward angles > 90°. This increase is successfully described in terms of the DWBA incorporated in the Coupled Reaction Channels program (FRESCO) by taking into account the contribution of α-cluster transfer between ¹⁴N and ¹⁰B. We have extracted the spectroscopic amplitude for the configuration ¹⁴N→α+¹⁰B by taking into consideration the two possibilities of transfer to L=2 and L=4 orbitals individually. The extracted SA₂ and SA₄ values are 0.58±0.10 and 0.81±0.12, respectively. The extracted SA₂ value overestimates the known theoretical value, whereas the SA₄ value is close to the previously reported one (SA = 0.83). The extracted spectroscopic amplitude for the configuration of ¹⁴N as an α-particle coupled to a ¹⁰B core suggests that the elastic transfer process is a strong component in the total elastic scattering cross sections. The investigation of the ¹⁰B(¹⁴N,¹⁰B)¹⁴N α-cluster transfer process by taking into consideration the transfer to L=2 and L=4 orbitals simultaneously showed that the average extracted values for SA₂ and SA₄ are 0.5±0.17 and 0.74±0.08, respectively, which agree well with the calculations for transfer process to L=2 and L=4 orbitals individually.
It is shown that the obtained values of the depths of the real and imaginary potentials linearly depend on energy in the energy range from 20 to 100 MeV.
A. A. Ibraheem extends his appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program under grant number G.R.P-56-41.