HTML
--> --> -->The KamLAND [1–4] and Borexino [5–7] experiments have made pioneering contributions to the discovery of geoneutrinos. Their detection is achieved by detecting inverse-beta-decay (IBD) signals in liquid-scintillator detectors. An IBD signal consists of a prompt positron signal and a delayed neutron-capture signal, and the prompt-delay-coincidence provides a clear signature of the interaction. The IBD cross-section is relatively high. The energy threshold for the reaction is 1.8 MeV, and only
Neutrinos originating in the mantle have a direct connection with the power that drives plate tectonics and mantle convection [9, 10]. However, the measurements on mantle geoneutrinos rely heavily on crust geoneutrino predictions. Consequently, the mantle component still has considerable uncertainty. In Ref. [11], Tanaka and Watanabe proposed to use a 6Li-load liquid scintillator to extract directional information on U and Th neutrinos using the IBD process and even image the Earth’s interior.
The K element is more mysterious than U and Th.
Notably, thus far, the liquid scintillator detector of Borexino is the only one that achieved sub-MeV neutrino spectroscopy, where both large target mass and low background are realized. Solar neutrinos are detected through neutrino-electron scattering,
$ \nu+e^- \rightarrow \nu+e^-, $  | (1) |
Because of the long emission time constant of scintillation radiation, the new type of liquid-scintillator Cherenkov neutrino detectors [15–17] can identify the small prompt Cherenkov radiation within the large amount of slow scintillation light. This unique feature can provide not only the reconstruction of both direction and energy, which has never been achieved in conventional liquid scintillation neutrino detectors, but also particle identification [18]. We consider two schemes for the liquid-scintillator Cherenkov neutrino detector. The first approach is to use a fast, high-light-yield liquid scintillator and fast photon detectors. In this case, the light yield can reach 10,000 photons per MeV with an emission time constant of a few nanoseconds, which is much longer than several picoseconds of timing precision of the photon detectors. The recent experimental development for this approach can be found in Refs. [19–21]. The second approach is to use a slow liquid scintillator and photomultiplier tubes (PMTs). The PMTs usually have a timing precision of about one nanosecond, while the emission time constant for the slow liquid scintillator is much longer, for example, 20 nanoseconds [22–24].
In this study, we focus on the latter scheme. We adopted the parameter set for pure linear alkylbenzene (LAB) [22] as a slow liquid-scintillator candidate, which is most favorable for the Cherenkov separation. The light yield is 2530 photons/MeV, and the emission rise and decay time constants are 12.2 ns and 35.4 ns, respectively. The time profile is shown in Fig. 1. The Cherenkov threshold is 0.178 MeV, assuming the refractive index of the liquid to be 1.49 [25].
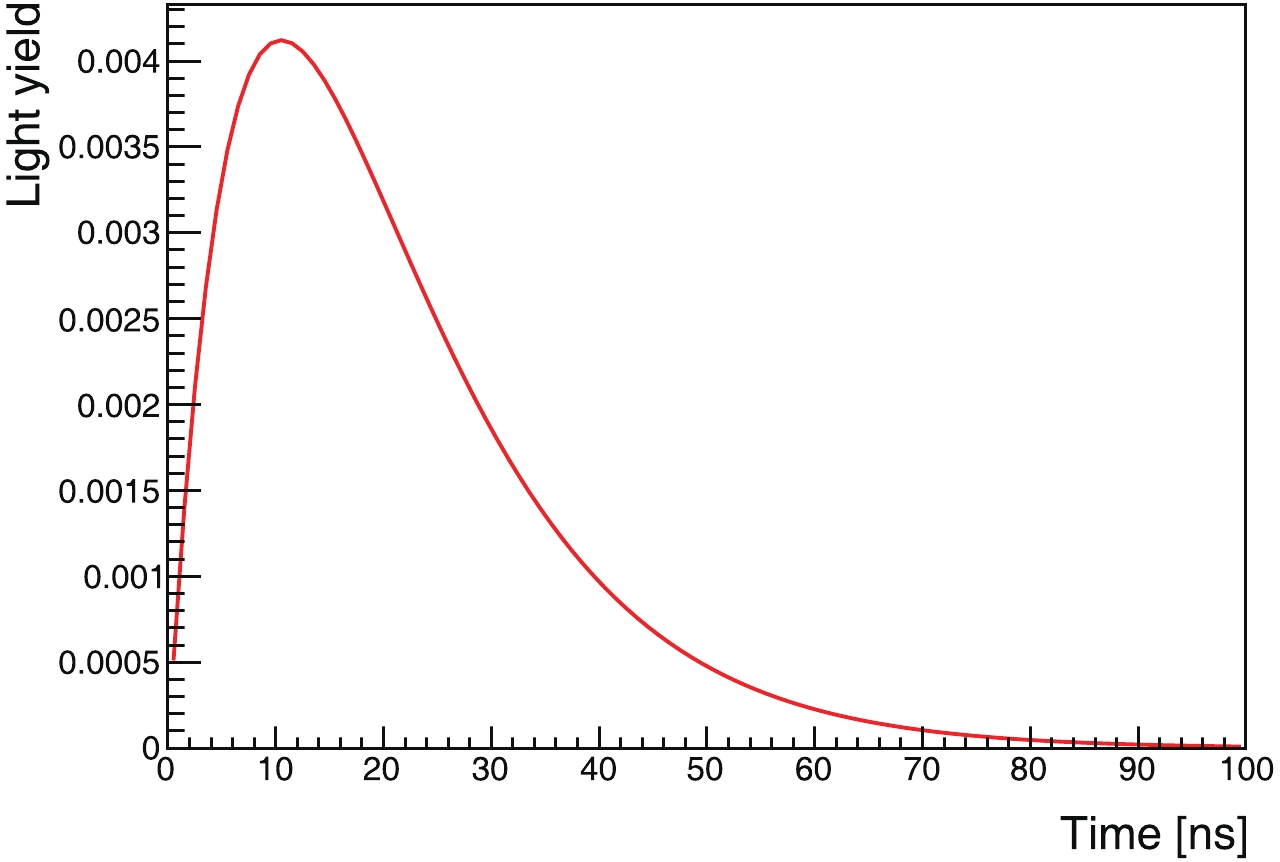 Figure1. (color online) Normalized time profile of scintillation light emitted by slow liquid scintillator, LAB [22].
Figure1. (color online) Normalized time profile of scintillation light emitted by slow liquid scintillator, LAB [22].2.1.Ideal expectation with a terrestrial detector
We consider an ideal terrestrial detector, located at the Earth’s equator, rotating along with the Earth. We define the solar z-axis, Figure2. (color online) Definitions of
Figure2. (color online) Definitions of  Figure3. (color online) Theoretical distributions of
Figure3. (color online) Theoretical distributions of 2
2.2.Liquid-scintillator Cherenkov detector simulation
We adopted the detector scheme [26] shown in Fig. 4. The slow liquid scintillator, which is contained in a transparent container, is in the center, and it is surrounded by a non-scintillating material, such as water or mineral oil. The PMTs are installed with all photocathodes facing inward, forming a large spherical array. The PMTs are all immersed in the water or oil. The water behind the PMTs also serves as a veto layer, shielding the detector from radioactivities like betas, gammas, neutrons, and cosmic-ray muons. The number of signals is directly proportional to the target mass, and due to the required low-background rate, only the central region of the liquid scintillator, known as the fiducial volume, is accepted for signal detection. Figure4. (color online) Detector concept. Inside to outside: slow liquid scintillator (yellow), water (blue), PMT, and water.
Figure4. (color online) Detector concept. Inside to outside: slow liquid scintillator (yellow), water (blue), PMT, and water.The simulations of solar-neutrino generation, geo-neutrino generation, and neutrino-electron scattering are described in Appendix A, Appendix B, and Appendix C, respectively. Recoil electrons are simulated using Geant4 [27–29] including all possible electromagnetic processes. Because of multiple scattering, the initial direction of the electron is smeared out. Some electrons eventually turn back when they are close to stopping.
Both Cherenkov and scintillation light emissions are handled by Geant4; however, the production of scintillation light is customized according to LAB measurement [22].
All optical photons are recorded and undergo empirical simulations [26, 30], as the attenuation length of optical photons still requires more experimental research [22], and the target mass or volume is a parameter we want to test. The limited PMT photocathode coverage and photon attenuation and scattering will cause efficiency loss, hence we assume that practically only 66.7% (2/3) of the photons can reach the PMTs. The quantum efficiency of a PMT is assumed to be 30% for all photons within the range [300, 550] nm and to be zero for the rest, which is motivated by the high quantum efficiency of PMTs, according to Ref. [31]. In summary, the total efficiency for generating photoelectrons, PE, is 20% for photons within the range [300, 550] nm and zero outside of this wavelength range.
2
2.3.Energy and direction reconstruction
From the simulation, we can determine the average energy scale, i.e., the number of PE per MeV, and thus the total number of detected PEs for each event is scaled to the detected energy. The detected-energy spectra of solar- and geo-neutrinos are shown in Fig. 5 and Fig. 6, respectively. Figure5. (color online) Detected kinetic-energy spectra of recoiling electrons produced by solar neutrinos in simulation.
Figure5. (color online) Detected kinetic-energy spectra of recoiling electrons produced by solar neutrinos in simulation.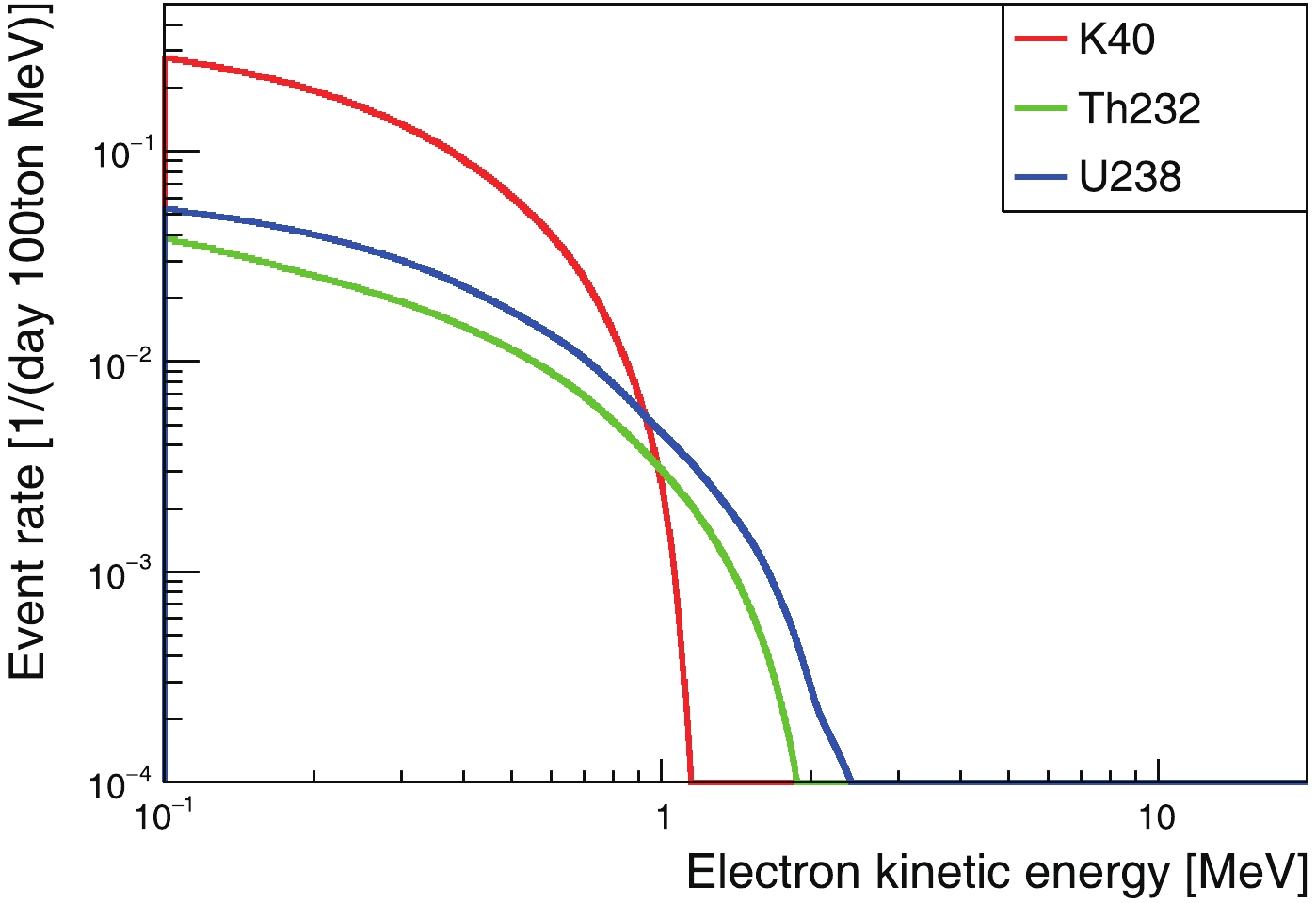 Figure6. (color online) Detected kinetic-energy spectra of recoiling electrons produced by geoneutrinos in simulation.
Figure6. (color online) Detected kinetic-energy spectra of recoiling electrons produced by geoneutrinos in simulation.We use a weighted-center method to reconstruct the direction of the recoiling electrons,
$ \vec{R} = \frac{1}{N_{\rm{PE}}}\sum\limits_{i = 1}^{N_{\rm{PE}}} \vec{r}_{i}, $  | (2) |
We attempted three groups of photons. In Case (1), we use all Cherenkov photons to study the best case and understand the scattering of electrons in the liquid scintillator. In Case (2), we apply the 20% efficiency cut, as described in Section 1.2. We use this study to understand the results with Cherenkov photons only. In Case (3), we tested a more realistic case, where the detection efficiency is considered, and the photoelectrons from the first two ns of scintillation radiation are introduced.
The angular response is plotted in Fig. 7 for electrons with kinetic energies in the range of [0.5, 2] MeV, where we show the cosine of the angle between the reconstructed direction and the initial electron direction for all three cases. For case (1), the angular resolution with 99% coverage is 116 degrees, and it is 124 and 125 degrees for the second and third cases, respectively. Comparing Case (1) with (2), which includes the 20% efficiency cut, the latter does not show significant degradation of the reconstructed angular distribution. The dominant factor affecting the performance of directional reconstruction is electron scattering in the liquid scintillator. After further introducing the scintillation photons as the background in Case (3), we find that the angular resolution is slightly worse than for Case (2). In the rest of this paper, we focus on Case (3), which is the more realistic one.
 Figure7. (color online) Angular-response distribution of reconstructed directions relative to electrons’ initial direction, where the electron kinetic energy is in range [0.5, 2] MeV. Upper and lower panels are the same, but the upper panel is plotted on a logarithmic scale to clearly show the non-negligible negative component.
Figure7. (color online) Angular-response distribution of reconstructed directions relative to electrons’ initial direction, where the electron kinetic energy is in range [0.5, 2] MeV. Upper and lower panels are the same, but the upper panel is plotted on a logarithmic scale to clearly show the non-negligible negative component.The angular response as a function of energy is shown in Fig. 8 for Case (3). The resolution improves gradually with increasing energy.
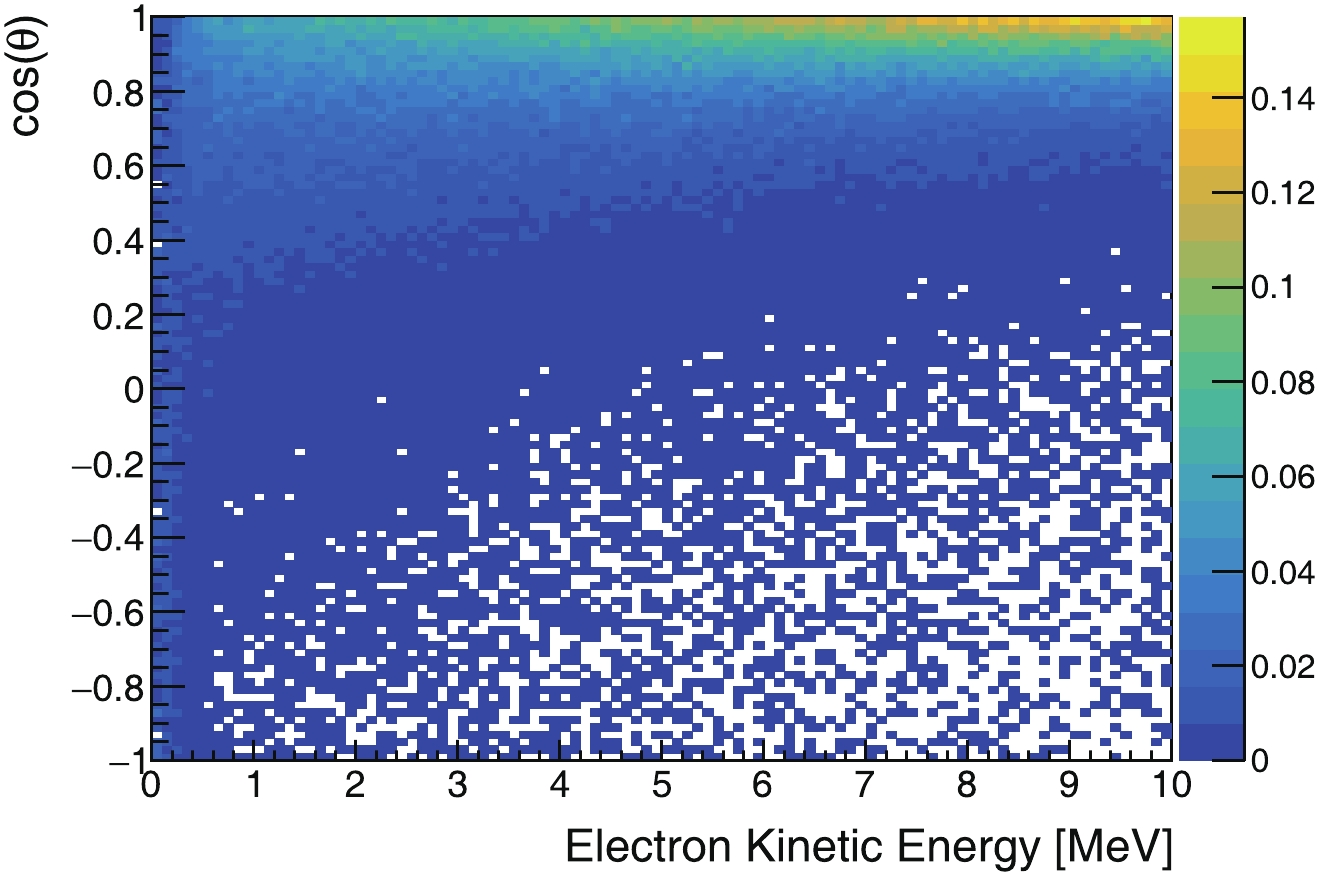 Figure8. (color online) Angular response versus energy. Projection on cos(θ) for [0.5, 2] MeV electrons is shown in Fig. 7.
Figure8. (color online) Angular response versus energy. Projection on cos(θ) for [0.5, 2] MeV electrons is shown in Fig. 7.2
2.4.Signal extraction
To extract the geoneutrino signals, we first determine an energy cut and a3
2.4.1.Determination of signal region
The event rate ratio of geo- to solar neutrinos as a function of energy is shown in Fig. 9, according to which we define three observation windows. One is the energy range [0.7, 2.3] MeV, where all Figure9. (color online) Signal-to-background ratio (geo-to-solar-neutrino ratio) as a function of electron kinetic energy.
Figure9. (color online) Signal-to-background ratio (geo-to-solar-neutrino ratio) as a function of electron kinetic energy.Followingly, we determine the
 Figure10. (color online) The
Figure10. (color online) The 3
2.4.2.Signal measurement
Using the data sample from our imagined experiment, the number of geoneutrino signals, $ N_{\rm geo} = N_{\rm can}-N_{\rm bkg}\times \epsilon, $  | (3) |
The uncertainty
$ \sigma_{\rm geo} = \sqrt{\sigma_{\rm candidate}^2 + N_{\rm solar}^2\sigma_{\epsilon}^2 + \epsilon^2\sigma_{\rm solar}^2}, $  | (4) |
For the solar-neutrino background, pep and B8 neutrinos are dominant. We expect that several proposed experimental approaches, like Jinping [32], LENA [33], THEIA [17], and [34], will improve their uncertainty to a 1% precision. Calibration sources can be deployed to multiple locations of the detector [35]. The calibration source can be a beta source enclosed in a small metal box with a small pinhole as a collimator. With sufficient statistics, a 1% precision is expected.
From our experience, we assume that the detection-efficiency uncertainty, including the energy and the
For the
2
2.5.Sensitivity curve
From the discussion above and the results obtained for angular resolution and expected systematic uncertainties, we can now estimate the precision of the geoneutrino-flux measurement as a function of exposure. We express the sensitivity as $ {\rm sensitivity} = N_{\rm geo}/\sigma_{\rm geo}, $  | (5) |
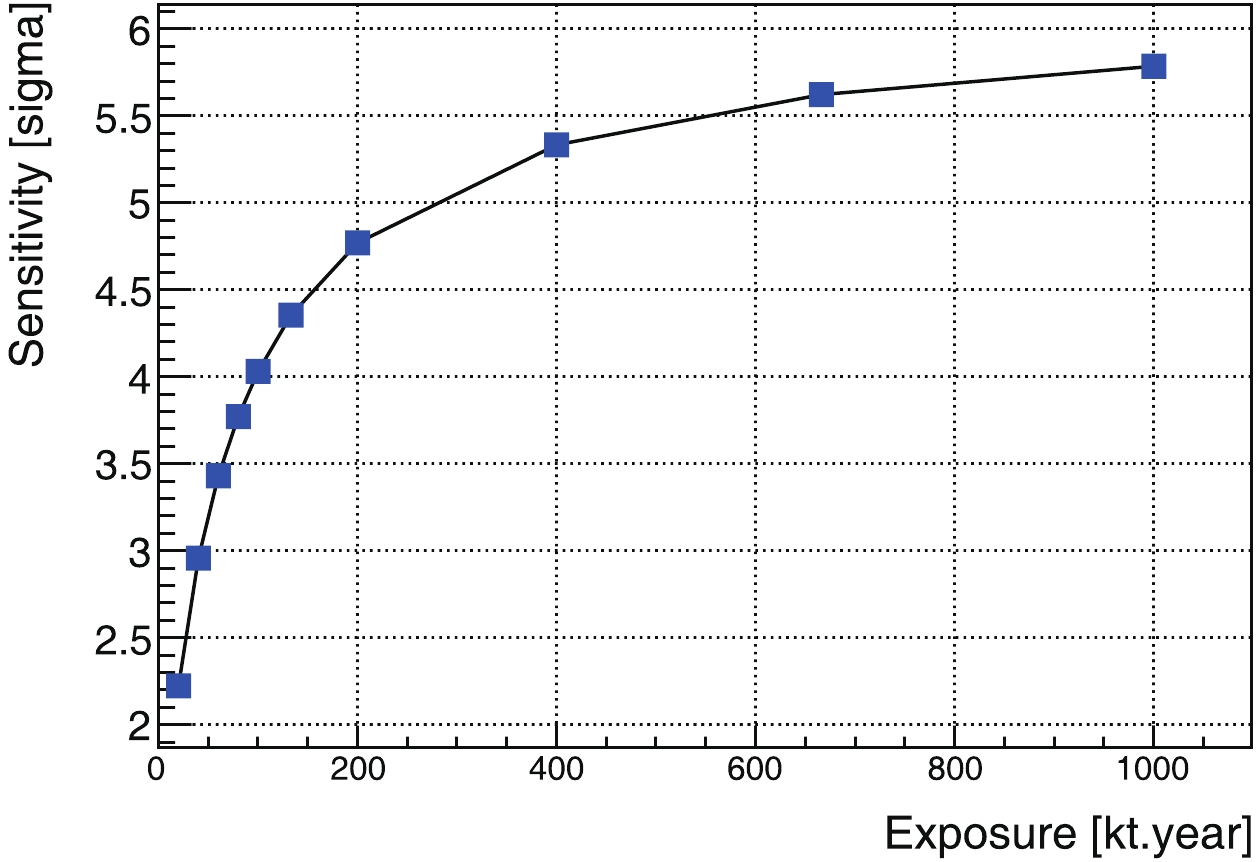 Figure11. (color online) Discovery sensitivity for all geoneutrinos as a function of exposure.
Figure11. (color online) Discovery sensitivity for all geoneutrinos as a function of exposure. Figure12. (color online) Discovery sensitivity for 40K geoneutrinos as a function of exposure.
Figure12. (color online) Discovery sensitivity for 40K geoneutrinos as a function of exposure. Figure13. (color online) Discovery sensitivity for 238U and 232Th genoneutrinos as a function of exposure.
Figure13. (color online) Discovery sensitivity for 238U and 232Th genoneutrinos as a function of exposure.Among these results, the most attractive is the one for the
For the
2
3.1.Neutrino-electron scattering
The directional reconstruction of the recoil electrons is crucial for the overall performance of this detection scheme. The angular resolution governs the final signal-to-background ratio. We find that the scattering of the electrons in the LAB has a primary effect on the resolution. Reconstruction with a limited number of Cherenkov photoelectrons is only the secondary factor, as presented. The density of the LAB is2
3.2.Slow liquid scintillator
In this study, we assumed a 66.7% detection efficiency, considering the PMT photocathode coverage, photon attenuation in the detector, and a 30% quantum efficiency for photons in the range [300, 550] nm. The detection efficiency is the most optimistic assumption in this entire study. The scintillation emission spectrum of the pure LAB peaks at 340 nm [22], which is close to the UV side and may suffer more absorption than expected. The absorption is caused by the intrinsic absorption band of LAB and cannot be resolved by purification. With the addition of wavelength-shifting materials, the peak can be shifted into the visible range. The absorption could be more severe, and some part of the Cherenkov light can be lost. We hope that this investigation will stimulate further relevant slow-liquid-scintillator research, such as the search for a new solvent and a new wavelength shifter.2
3.3.Other background
In this study, we included the critical solar-neutrino background; however, other intrinsic or environmental radiative backgrounds should be considered as well. We take the situation of solar neutrino study at the Borexino experiment as an example [36, 37] to explain our expectations. The radioactiveReactor-neutrino backgrounds can be avoided by selecting an experimental site far away from commercial reactors, like the Jinping underground laboratory [32, 40, 41]. Reactor-neutrino fluxes can be efficiently constrained to perform better than 6% [35, 42–44]. The reactor-neutrino background can also be measured in-situ, hence this is not a critical issue.
2
3.4.Mantle neutrinos
Knowledge of mantle neutrinos is likewise necessary. However, it is only about 30% of the total geoneutrino flux if the detector is placed on a continental site, while the rest originates from the crust. Given the current sensitivity in measuring the total flux and the current angular resolution, we did not pursue this issue further.    | Flux/(      | |
  | 0.42 |   |
  | 0.38 |   |
| 0.86 |   | |
  | 1.45 |   |
  | 1.19 |   |
  | 1.73 |   |
  | 1.74 |   |
  | 15.8 |   |
  | 18.5 |   |
TableA1.Characteristic energies and total fluxes of solar neutrinos.
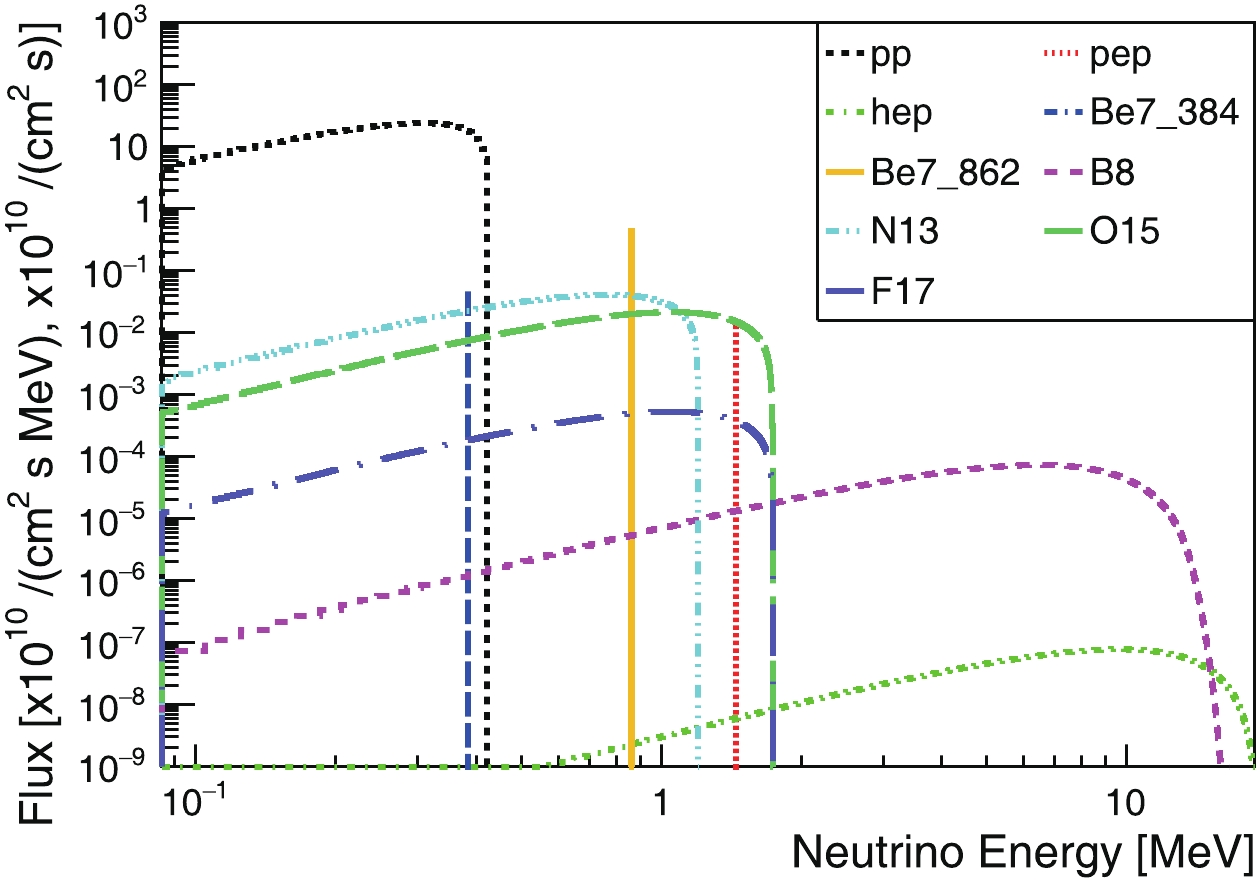 FigureB1. (color online) Predicted non-oscillating solar electron-neutrino energy spectra on Earth, where the unit for continuous spectra is 1010/(cm2 s MeV), and for discrete lines is 1010/(cm2 s).
FigureB1. (color online) Predicted non-oscillating solar electron-neutrino energy spectra on Earth, where the unit for continuous spectra is 1010/(cm2 s MeV), and for discrete lines is 1010/(cm2 s).Solar neutrinos are generated as pure electron neutrinos. Taking into account the oscillation between different neutrino flavors during transit
$\tag{A1} P^{\odot}_{ee} = \cos^4\theta_{13}\left(\frac{1}{2}+\frac{1}{2}\cos2\theta^M_{12}\cos2\theta_{12}\right), $  |
The appearance probability of
$\tag{A2} P^{\odot}_{e\mu(\tau)} = 1-P^{\odot}_{ee}. $  |
$\tag{B1} \begin{align} ^{238}\rm{U} \rightarrow ^{206}\rm{Pb} + 8\alpha + 6e^- + 6\bar\nu_e + 51.698\; MeV, \end{align} $  |
$\tag{B2} \begin{align} ^{232}\rm{Th} \rightarrow ^{207}\rm{Pb} + 7\alpha + 4e^- + 4\bar\nu_e + 46.402\; MeV, \end{align} $  |
$\tag{B3} ^{40}\rm{K} \rightarrow ^{40}\rm{Ca} + e^- + 4\bar\nu_e + 1.311\; MeV\; (89.3\%), $  |
$\tag{B4} ^{40}\rm{K} + e^- \rightarrow ^{40}\rm{Ar} + \nu_e + 1.505\; MeV\; (10.7\%). $  |
| Isotope |   | Flux/(      | |
| Crust | 40K | 1.31 | 0.00160 |
| 232Th | 2.26 | 0.00043 | |
| 238U | 3.27 | 0.00047 | |
| Mantle | 40K | 1.31 | 0.00057 |
| 232Th | 2.26 | 0.00005 | |
| 238U | 3.27 | 0.00008 |
TableB1.Characteristic energies and total fluxes of geoneutrinos. EMax depicts maximum energy for continuous spectra.
 FigureB2. (color online) Predicted non-oscillating geo electron-antineutrino energy spectra on the Earth's surface.
FigureB2. (color online) Predicted non-oscillating geo electron-antineutrino energy spectra on the Earth's surface.We used a layered Earth model to simulate the geoneutrinos. In this model, the Earth is assumed to consist of three layers: the core, mantle, and crust. We assume that the mantle and crustal layers have uniform distributions of
The entire volume of the Earth is divided into many small cells, each of which has a coordinate
$\tag{B5} {\rm d}\phi(\vec{r})_{e} = \frac{X \lambda N_A}{\mu} n_{\nu} P_{ee}^\oplus \frac{A(\vec r) \rho(\vec{r})}{4\pi |\vec{r}-\vec{d}|^2}{\rm d}v, $  |
We take the outer radii of the core, mantle and crust to be 3480, 6321, and 6371 km [52], respectively, with their corresponding densities at 11.3, 5.0, and 3.0 g/cm3. The element abundances of K, Th, and U are set to match the integrated flux predictions, as in Refs. [40, 41], and the values are given in Table B2. This simplified layered model is not as sophisticated as that provided in Ref. [53]; however, it is nevertheless sufficient for our demonstration purposes. The rest of the parameters are taken from Ref. [41]. The total fluxes of the predicted geoneutrinos are summarized in Table B1. The non-oscillating neutrino spectra of
| K [kg/kg] | Th [kg/kg] | U [kg/kg] | |
| Crust | 1.16 × 10?2 | 5.25 × 10?6 | 1.35 × 10?6 |
| Mantle | 152 × 10?6 | 21.9 × 10?9 | 8.0 × 10?9 |
TableB2.Element abundance of K, Th and U in the mantle and crust used for this study.
The geoneutrino oscillation probability varies only by about 2% within the energy range [0, 3.5] MeV [40], hence it is treated as a constant, i.e.,
$ \tag{B6} P^{\oplus}_{e\mu(\tau)} = 1-P^{\oplus}_{ee}. $  |
$\tag{C1} \frac{{\rm d}\sigma(E_{\nu},T_e)}{{\rm d}T_e} = \frac{\sigma_0}{m_e}\left[g_1^2+g_2^2\left(1-\frac{T_e}{E_{\nu}}\right)^2-g_1g_2\frac{m_eT_e}{E_{\nu}^2}\right], $  |
$ \tag{C2}\begin{split} g_1^{(\nu_e)} =& g_2^{(\bar\nu_e)} = \frac{1}{2}+\sin^2\theta_W\simeq0.73,\\ g_2^{(\nu_e)} =& g_1^{(\bar\nu_e)} = \sin^2\theta_W\simeq0.23, \end{split} $  |
$ \tag{C3} \begin{split} g_1^{(\nu_{\mu,\tau})} =& g_2^{(\bar\nu_{\mu,\tau})} = -\frac{1}{2}+\sin^2\theta_W\simeq-0.27,\\ g_2^{(\nu_{\mu,\tau})} =& g_1^{(\bar\nu_{\mu,\tau})} = \sin^2\theta_W\simeq0.23. \end{split} $  |
$ \tag{C4} \sigma_0 = \frac{2G_F^2m_e^2}{\pi}\simeq88.06\times10^{-46}\ \rm{cm}^2. $  |
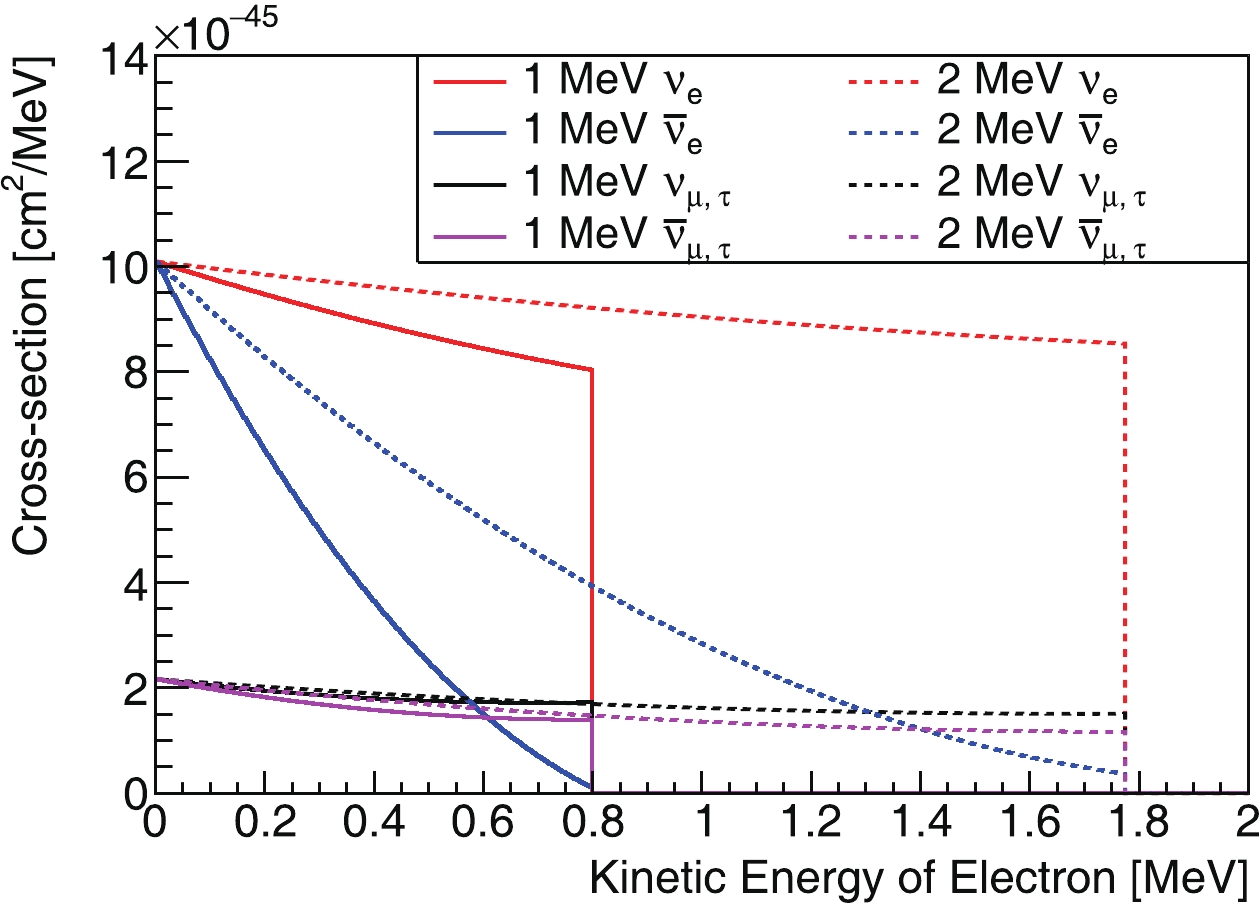 FigureC1. (color online) Neutrino-electron-scattering differential cross-section for
FigureC1. (color online) Neutrino-electron-scattering differential cross-section for With the above formulas, the distribution of the recoiling electrons' kinetic energy is calculated:
$\tag{C5} \frac{{\rm d}N}{{\rm d}T} = N_e\int \left [ \sum\limits_{\nu} \frac{{\rm d}\sigma(E_{\nu},T_e)}{{\rm d}T_e} P_{e\nu}\right ] F(E_{\nu}){\rm d}E_{\nu}, $  |
With the condition of energy and momentum conservation, the cosine of the scattering angle between the initial neutrino direction and the scattered-electron direction can be determined from:
$ \tag{C6} \cos\theta = \frac{1+m_e/E_{\nu}}{\sqrt{1+2m_e/T_e}}. $  |
 FigureC2. (color online) Cosine distribution of scattering angle between initial neutrino direction and recoiling electron. In this plot, we use 1 MeV
FigureC2. (color online) Cosine distribution of scattering angle between initial neutrino direction and recoiling electron. In this plot, we use 1 MeV After considering neutrino oscillation and neutrino-electron scattering, the kinetic energy spectrum of recoiling electrons of solar- and geo-neutrinos are shown in Fig. C3, and Fig. C4, respectively.
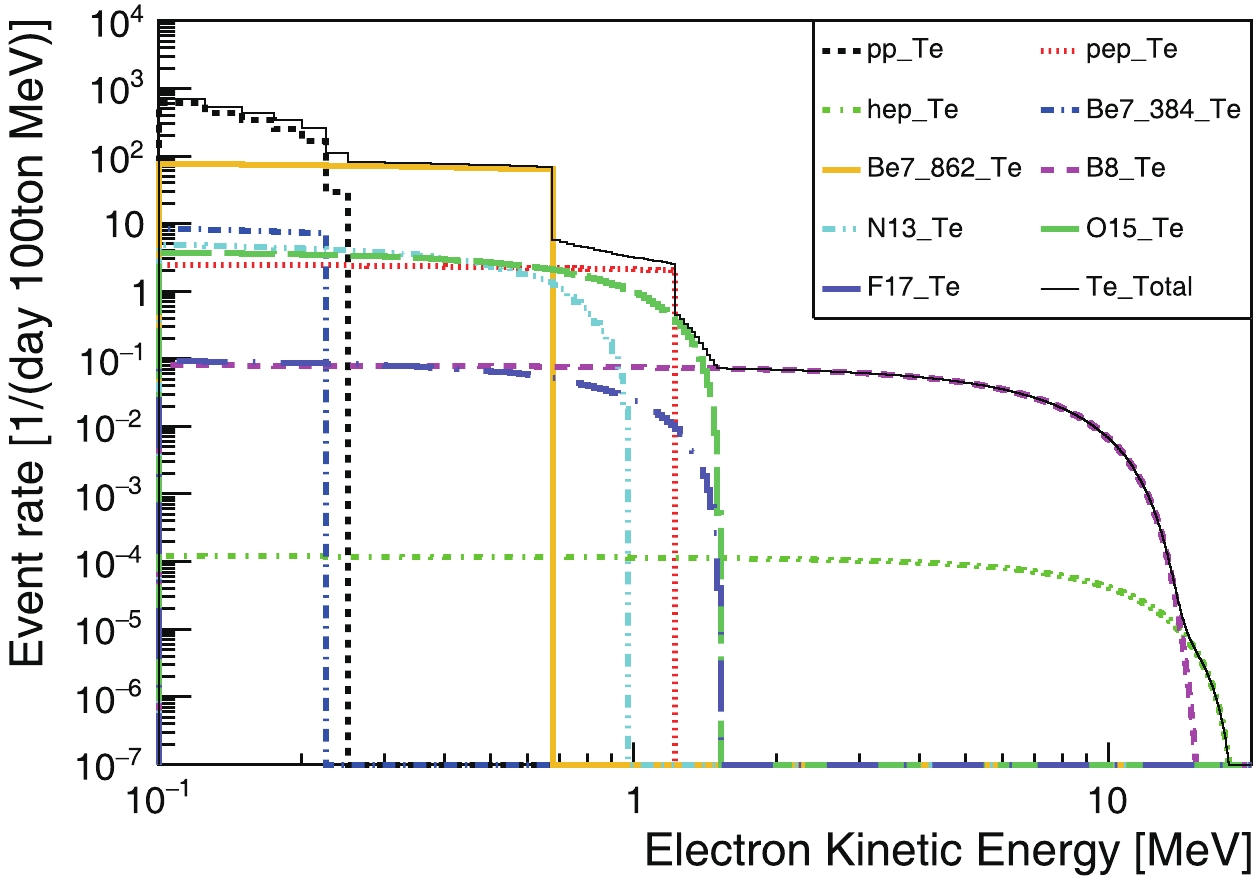 FigureC3. (color online) Recoiling-electron kinetic-energy spectra from solar neutrinos.
FigureC3. (color online) Recoiling-electron kinetic-energy spectra from solar neutrinos. FigureC4. (color online) Recoiling-electron kinetic-energy spectra from geo neutrinos.
FigureC4. (color online) Recoiling-electron kinetic-energy spectra from geo neutrinos.