Yun-Hua Chen ^,
,

Corresponding author: Yun-Hua Chen, yhchen@ustb.edu.cn

School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China
Received Date:2019-09-11
Available Online:2020-02-01
Abstract:We study the contributions of intermediate bottomonium-like $Z_b$ states and the bottom meson loops in the heavy quark spin flip transitions $\Upsilon(4S) \to h_b(1P,2P) \pi^+\pi^-$. Depending on the constructive or destructive interferences between the $Z_b$-exchange and the bottom meson loops mechanisms, we predict two possible branching ratios for each process: BR$_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-}\simeq\big(1.2^{+0.8}_{-0.4}\times10^{-6}\big)$ or $\big( 0.5^{+0.5}_{-0.2}\times10^{-6}\big)$, and $ {{BR}}_{\Upsilon(4S) \to h_b(2P)\pi^+\pi^-}\simeq \big(7.1^{+1.7}_{-1.1}\times10^{-10}\big)$ or $\big( 2.4^{+0.2}_{-0.1}\times10^{-10}\big)$. The contribution of the bottom meson loops is found to be considerably larger than that of the $Z_b$-exchange in the $\Upsilon(4S) \to h_b(1P) \pi\pi$ transitions, while its decay rates are not comparable to those of heavy quark spin conserved $\Upsilon(4S) \to \Upsilon(1S,2S) \pi\pi$ processes. We also predict the contribution of the charm meson loops in the branch fractions of $\psi(3S,4S) \to h_c(1P)\pi\pi$.

HTML

--> --> -->

Hadronic transitions $ \Upsilon(mS) \to \Upsilon(lS) \pi \pi $ and $ \Upsilon(mS) \to h_b(nP) \pi \pi $ are important processes for understanding heavy-quarkonium dynamics and low-energy quantum chromodynamics (QCD). Because bottomonia are expected to be compact and nonrelativistic, the QCD multipole expansion (QCDME) method [1–4] is often used to analyze these transitions, where pions are emitted because of the hadronization of soft gluons. The decay rates of $ \Upsilon(2S,3S) \to \Upsilon(1S,2S) \pi \pi $ can be well described by QCDME [5]. Because the total spin of $ b\bar{b} $ system in $ \Upsilon(mS) $ and $ h_b(nP) $ are 1 and 0, respectively, in general, the heavy quark spin flip $ \Upsilon(mS) \to h_b(nP)\pi\pi $ processes are expected to be suppressed, compared with the heavy quark spin conserved $ \Upsilon(mS) \to \Upsilon(nS)\pi\pi $ processes. Within the framework of QCDME, studies [5–7] predicted that the branching fraction of $ \Upsilon(3S) \to \Upsilon(1P) \pi \pi $ is suppressed by two orders of magnitude, relative to that of $ \Upsilon(3S) \to \Upsilon(1S) \pi \pi $, while Ref. [8] predicted a suppression of at least three orders of magnitude. The prediction of Ref. [8] is supported by experimental data [9]. In the decay processes $ \Upsilon(5S) \rightarrow \Upsilon(lS) \pi^+ \pi^- $ ($ l = 1, 2, 3 $) and $ \Upsilon(5S) \rightarrow h_b(nP) \pi^+ \pi^- $ ($ n = 1, 2 $) where the two charged bottomoniumlike resonances $ Z_b(10610)^\pm $ and $ Z_b(10650)^\pm $ were observed, $ \Upsilon(5S) \rightarrow h_b(nP) \pi^+ \pi^- $ proceeds at a rate comparable to the $ \Upsilon(5S) \rightarrow \Upsilon(lS) \pi^+ \pi^- $ processes [10, 11]. The mechanism that mitigates this expected suppression has remained controversial. In Refs. [12, 13], the $ \Upsilon(5S) \rightarrow h_b(nP) \pi^+ \pi^- $ processes were interpreted via bottom meson loops mechanism, while genuine S-matrix $ Z_b $ poles are required as in Refs. [14–17]. The meson loops mechanism has been investigated by many previous works [18–24] to study the dipion and $ \eta $ transitions of higher charmonia and bottomonia because the branch ratios and dipion invariant mass spectra cannot be described by QCDME.
In this work, we will study whether the bottom meson loops mechanism can produce the $\Upsilon(4S) \rightarrow $$ h_b(nP) \pi^+ \pi^- $ transitions at decay ratios comparable to $ \Upsilon(4S) \rightarrow $$ \Upsilon(lS) \pi^+ \pi^- $. Because in the dipion emission processes of the $ \Upsilon(4S) $ the crossed-channel exchanged $ Z_b $ cannot be on-shell, these transitions are expected to be good channels to study the bottom meson loops' effect. In our previous works [25, 26], by using the nonrelativistic effective field theory (NREFT), we calculated the effects of the bottom meson loops as well as the $ Z_b $-exchange in the $ \Upsilon(4S) \to \Upsilon(1S,2S) \pi \pi $ processes, and we found that the experimental data can be described well. Here, within the same theoretical scheme, we will calculate the contributions of the bottom meson loops and $ Z_b $-exchange in the $ \Upsilon(4S) \rightarrow h_b(nP) \pi^+ \pi^- $ processes, and give theoretical predictions for the decay branching ratios. We find that the contribution of the bottom meson loops is considerably larger than that of the $ Z_b $-exchange in the $\Upsilon(4S) \rightarrow $$ h_b(1P) \pi^+ \pi^- $ process, and it cannot produce a rate comparable to that of $ \Upsilon(4S) \rightarrow \Upsilon(1S,2S) \pi^+ \pi^- $.
The remainder of this paper is organized as follows. In Sec. 2, the theoretical framework is described in detail. In Sec. 3, we provide the theoretical predictions for the decay branching fractions of $ \Upsilon(4S) \rightarrow h_b(1P,2P) \pi^+ \pi^- $, and discuss the contributions of different mechanisms. The study is concluded in Sec. 4.

2

-->

2.1.Lagrangians

To calculate the contribution of the mechanism $ \Upsilon(mS) \to Z_b\pi \to h_b(nP) \pi\pi $, we need the effective Lagrangians for the $ Z_b \Upsilon\pi $ and $ Z_b h_b\pi $ interactions [27],

$ {\cal L}_{Z_b\Upsilon\pi} = \sum\limits_{j = 1,2}C_{Z_{bj}\Upsilon(mS)\pi} \Upsilon^i(mS) \langle {Z^i_{bj}}^\dagger u_\mu \rangle v^\mu +\mathrm{h.c.} \,, $

(1)

$ {\cal L}_{Z_b h_b\pi} = \sum\limits_{j = 1,2}g_{Z_{bj}h_b(nP)\pi}\epsilon_{ijk} \langle {Z^i_{bj}}^\dagger u^j \rangle h_b^k +\mathrm{h.c.} \,, $

(2)

where $ Z_{b1} $ and $ Z_{b2} $ denote $ Z_b(10610) $ and $ Z_b(10650) $, respectively, and $ v^\mu = (1,{\bf{0}}) $ is the velocity of the heavy quark. The $ Z_b $ states are given in the matrix as

$ Z^i_{bj} = \left( {\begin{array}{*{2}c} \dfrac{1}{\sqrt{2}}Z^{0i}_{bj} & Z^{+i}_{bj} \\ Z^{-i}_{bj} & -\dfrac{1}{\sqrt{2}}Z^{0i}_{bj} \end{array}} \right)\,. $

(3)

The pions can be parametrized as Goldstone bosons of the spontaneous breaking of the chiral symmetry:

$\begin{split}{u_\mu } = &{\rm i}\left( {{u^\dagger }{\partial _\mu }u{\mkern 1mu} - {\mkern 1mu} u{\partial _\mu }{u^\dagger }} \right){\mkern 1mu} ,\;\;\;\;u = \exp (\dfrac{{{\rm i}\Phi }}{{\sqrt 2 {F_\pi }}}){\mkern 1mu} ,\\\Phi =& \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}{\pi ^0}}&{{\pi ^ + }}\\{{\pi ^ - }}&{ - \frac{1}{{\sqrt 2 }}{\pi ^0}}\end{array}} \right),\end{split}$

(4)

where $ F_\pi = 92.2 \,\rm{MeV} $ is the pion decay constant.
To calculate the box diagrams, we need the Lagrangian for the coupling of the $ \Upsilon $ to the bottom mesons and the coupling of the $ h_b $ to the bottom mesons [27, 28],

$ {\cal L}_{\Upsilon HH} = \frac{{\rm i}\, g_{JHH}}{2} \langle J^\dagger H_a {{\sigma}}\cdot \!\overleftrightarrow{\partial}\! \bar{H}_a \rangle + {\rm h.c.}\,, $

(5)

$ {\cal L}_{h_b HH} = \frac{{\rm i}\, g_{1}}{2} \langle h_b^{\dagger i} H_a \sigma^i\bar{H}_a \rangle + {\rm h.c.}\,, $

(6)

where $ J \equiv {\bf{\Upsilon}} \cdot {{\sigma}}+\eta_b $ denotes the heavy quarkonia spin multiplet, $ H_a = {{V}}_a \cdot {{\sigma}}+P_a $ with $ P_a(V_a) = (B^{(*)-},\bar{B}^{(*)0}) $ collects the bottom mesons, and $ A\overleftrightarrow{\partial}\!B\equiv A(\overrightarrow{\partial}B)-(\overrightarrow{\partial}A)B $. We also need the Lagrangian for the axial coupling of the pion fields to the bottom and antibottom mesons, which at the lowest order in heavy-flavor chiral perturbation theory is given by [29–33]

$ {\cal L}_{HH\Phi} = \frac{g_\pi}{2} \langle \bar{H}_a^\dagger {{\sigma}} \cdot {{u}}_{ab} \bar{H}_b \rangle -\frac{g_\pi}{2} \langle H_a^\dagger H_b {{\sigma}} \cdot {{u}}_{ba} \rangle, $

(7)

where $ u^i = -\sqrt{2}\partial^i \Phi/F + \mathcal{O}(\Phi^3) $ denotes the three-vector components of $ u_\mu $, as defined in Eq. (4). Here, we use $ g_\pi = 0.492\pm0.029 $ from a recent lattice QCD calculation [34].
2 -->

2.2.Power counting of loops

Because the $ \Upsilon(4S) $ meson is above the $ B\bar{B} $ threshold and decays predominantly into $ B\bar{B} $ pairs, the loop mechanism with intermediate bottom mesons may be important in the transitions $ \Upsilon(4S) \rightarrow h_b(nP) \pi^+\pi^- $. By following the formalism set-up based on NREFT [28, 35, 36], we will analyze the power counting of different types of loops. In NREFT, the expansion parameter is the velocity of the intermediate heavy meson, namely $ \nu_X = \sqrt{|m_X-m_{B^{(*)}}-m_{B^{(*)}}|/m_{B^{(*)}}} $, which is small because the bottomonia X are close to the $ B^{(*)}\bar{B}^{(*)} $ thresholds. In this power counting, each nonrelativistic propagator scale as $ 1/\nu^2 $, and the measure of one-loop integration scales as $ \int {\rm d}^4 l \sim \nu^5 $.
There are five different kinds of loop contributions, namely the box diagrams displayed in Fig. 1(b), (c), triangle diagrams displayed in Fig. 2(a)–(c), and the bubble loop in Fig. 2(d). We analyze them one by one as follows:
Figure1. Feynman diagrams considered for $\Upsilon(mS) \rightarrow h_b(nP) \pi \pi $ processes. Crossed diagrams of (a) and (b) are not shown explicitly.

Figure2. Loop diagrams not considered in the calculations. The corresponding power counting arguments are given in the main text.

First, we analyze the power counting of the box diagrams, namely Fig. 1(b), (c). As shown in Eq. (7), the vertex of $ B^{(*)}B^{(*)}\pi $ is proportional to the external momentum of the pion $ q_\pi $. The $ \Upsilon B^{(*)}\bar{B}^{(*)} $ vertex is in a P-wave, and the $ h_bB^{(*)}\bar{B}^{(*)} $ vertex is in an S-wave; therefore, the loop momentum must contract with the external pion momentum, and hence the P-wave vertex scales as $ \mathcal{O}(q_\pi) $. Thus, the box diagrams scales as $ \nu^5 q_\pi^3/\nu^8 = q_\pi^3/\nu^3. $
For the triangle diagram Fig. 2(a), the leading $ \Upsilon B^{(*)}\bar{B}^{(*)}\pi $ vertex given by $ g_{JHH\pi} \langle J \bar{H}_a^\dagger H_b^\dagger \rangle u_{ab}^0 $ [37] is proportional to the energy of the pion, $ E_\pi\sim q_\pi $. Therefore, Fig. 2(a) is counted as $ m_B\nu^5 q_\pi^2/\nu^6 = m_B q_\pi^2/\nu $, where the factor $ m_B $ is introduced to match the dimension with the scaling for the box diagrams.
In Fig. 2(b), the leading $ h_b B^{(*)}\bar{B}^{(*)}\pi $ vertex given by $ g_{h_b HH\pi} \langle h_b^{\dagger i} H_a \sigma^j \bar{H}_b \rangle \epsilon_{ijk} u_{ab}^k $ [29] is proportional to the momentum of the pion $ q_\pi $. The loop momentum due to the $ \Upsilon B^{(*)}\bar{B}^{(*)} $ coupling has to contract with the external pion momentum. Thus, Fig. 2(b) scales as $ \nu^5 q_\pi^3/\nu^6 = q_\pi^3/\nu $.
The leading $ B^{(*)}B^{(*)}\pi\pi $ vertex comes from the chiral derivative term $ \langle H_a^\dagger({\rm i}D_0)_{ba}H_b \rangle = \langle H_a^\dagger({\rm i}\partial_0-{\rm i}V_0)_{ba}H_b \rangle $ [38, 39], in which the pion pair produced by the vector current, $ V^\mu = \frac{1}{2}(u^\dagger \partial^\mu u+u\partial^\mu u^\dagger) $, cannot form a positive-parity and C-parity state; therefore, this leading vertex does not contribute to the $ \Upsilon(mS) \rightarrow h_b(nP) \pi \pi $ processes. Isoscalar, $ PC = ++ $ pion pairs only enter in the next order $ \mathcal{O}(q_\pi^2) $ from point vertices. Therefore, Fig. 2(c) scales as $ \nu^5 q_\pi^3 /\nu^6 = q_\pi^3/\nu $.
In Fig. 2(d), both the initial and final vertices are proportional to $ q_\pi $; therefore, the bubble loop scales as $ m_B\nu^5 q_\pi^2 /\nu^4 = m_B q_\pi^2\nu $.
Therefore, we expect that the ratios of the contributions of the box diagrams, triangle diagram Fig. 2(a)–(c), and the bubble loop Fig. 2(d) are

$ \begin{aligned} \frac{ q_\pi^3}{\nu^3} : \frac{ m_B q_\pi^2}{\nu} : \frac{ q_\pi^3}{\nu} : \frac{ q_\pi^3}{\nu} : m_B q_\pi^2\nu = 1 : \frac{m_B \nu^2}{q_\pi} : \nu^2 : \nu^2 : \frac{m_B \nu^4}{q_\pi}\,, \end{aligned}$

(8)

where $ q_\pi \simeq (m_{\Upsilon(4S)}-m_{h_b(nP)})/2 $ and $ \nu = (\nu_{\Upsilon(4S)}+\nu_{h_b(nP)})/2 $, with $ \nu_{\Upsilon(4S)}\simeq 0.06 $, $ \nu_{h_b(1P)}\simeq 0.35 $, and $ \nu_{h_b(2P)}\simeq 0.24 $. Thus, for the $ \Upsilon(4S) \to h_b(1P) \pi^+\pi^- $ transition, the ratios in Eq. (8) are $ 1: 0.67 : 0.04 : 0.04 : 0.03 $. For the $\Upsilon(4S) \to h_b(2P) $$ \pi^+\pi^- $ transition, the ratios are $ 1: 0.75 : 0.02 : 0.02 : 0.02 $. Therefore, according to the power counting, the box diagrams and triangle diagram in Fig. 2(a) are dominant among the loop contributions, and they are of the same order. The $ \Upsilon(4S) $ is below the $ B^{(*)}\bar{B}^{(*)}\pi $ threshold, and the coupling $ g_{JHH\pi} $ in the triangle diagram Fig. 2(a) is unknown. Thus, for a rough estimation of the loop contributions, we will only calculate the box diagrams in the present study. All the box and triangle loop contributions discussed here are ultraviolet-finite and do not require additional introduction of counterterms.
2 -->

2.3.Tree-level amplitudes and box diagram calculation

The decay amplitude for

$ \Upsilon(mS)(p_a) \to h_b(nP)(p_b) \pi(p_c)\pi(p_d) $

(9)

is described in terms of the Mandelstam variables

$ s = (p_c+p_d)^2 , \quad t = (p_a-p_c)^2\,, \quad u = (p_a-p_d)^2 \,. $

(10)

By using the effective Lagrangians in Eqs. (1) and (2), the tree amplitude of $ \Upsilon(mS) \to Z_b\pi \to h_b(nP)\pi\pi $ can be obtained as

$ M_{Zb} = \frac{2 \sqrt{m_{\Upsilon(mS)}m_{h_b(nP)}}}{F_\pi^2}\epsilon_{abj}\epsilon_{\Upsilon(mS)}^a\epsilon_{h_b(nP)}^b\sum\limits_{i = 1,2}m_{Z_{bi}} C_{Z_{bi}\Upsilon(mS)\pi}g_{Z_{bi}h_b(nP)\pi} \bigg\{ p_c^0 p_d^j\frac{1}{t-m_{Z_{bi}}^2}+p_d^0 p_c^j\frac{1}{u-m_{Z_{bi}}^2} \bigg\}\,. $

(11)

The nonrelativistic normalization factor $ \sqrt{m_Y} $ has been multiplied with the amplitude for every heavy particle, with $ Y = \Upsilon(mS), h_b(nP), Z_{bi} $. The widths of the $ Z_b $ states are neglected in the present study, because they are of the order of $ 10 \,{\rm{MeV}} $ and are considerably smaller than the difference between the $ Z_b $ masses and the $ \Upsilon(mS)\pi/h_b(nP)\pi $ threshold.
Now, we discuss the calculation of the box diagrams. In the box diagrams Fig. 1(b) and (c), we denote the top left intermediate bottom meson as M1, and the other intermediate bottom mesons as M2, M3, and M4, in counterclockwise order. For the pseudoscalar or vector content of $ [M1, M2, M3, M4] $, there are twelve possible patterns and we number them in order: 1, $ [PPPV] $; 2, $ [PPVV] $; 3, $ [PVPV] $; 4, $ [PVVP] $; 5, $ [VVPP] $; 6, $ [VPVP] $; 7, $ [VPPV] $; 8, $ [PVVV] $; 9, $ [VPVV] $; 10, $ [VVPV] $; 11, $ [VVVP] $; 12, $ [VVVV] $. For each pattern, we also need to consider six possibilities of different flavor of the intermediate bottom mesons: $ [B^{(*)+},B^{(*)-},B^{(*)+},B^{(*)0}] $, $ [B^{(*)+},B^{(*)-},$${\bar B}^{(*)0},B^{(*)0}] $, $ [B^{(*)0},{\bar B}^{(*)0},B^{(*)0},B^{(*)+}] $, $ [B^{(*)-},B^{(*)+},B^{(*)-},{\bar B}^{(*)0}] $, $ [{\bar B}^{(*)0},B^{(*)0}, B^{(*)+},B^{(*)-}] $, and $ [{\bar B}^{(*)0},B^{(*)0},{\bar B}^{(*)0},B^{(*)-}] $. The full amplitude contains the sum of all possible amplitudes.
For the tensor reduction of the loop integrals, it is convenient to define $ {{q}} = -{{{p}}_b} $ and thperpendicular momentum $ {{q}}_\perp = {{{p}}_c}-{{q}}({{q}}\cdot {{{p}}_c})/{{q}}^2 $, which satisfy $ {{q}} \cdot {{q}}_\perp = 0 $. The result of the amplitude of the box diagrams can be written as

$ \begin{split} M_{\rm{loop}} =& \epsilon_{\Upsilon(mS)}^a\epsilon_{h_b(nP)}^b \Big\{ \epsilon_{abi}q^i A_1+ \epsilon_{abi}q_\perp^i A_2 +\epsilon_{bij}q^i q_\perp^j q_\perp^a A_3 \\&+\epsilon_{bij}q^i q_\perp^j q^a A_4 +\epsilon_{aij}q^i q_\perp^j q_\perp^b A_5 +\epsilon_{aij}q^i q_\perp^j q^b A_6 \Big\}\,. \end{split}$

(12)

Details on the analytic calculation of the box diagrams and explicit expressions of $ A_i $ $ (i = 1,2,...,6) $ are given in Appendix A.
The decay width for $ \Upsilon(mS) \to h_b(nP)\pi\pi $ is given by

$ \Gamma = \int_{s_-}^{s_+} \int_{t_-}^{t_+}\frac{|M_{Zb}+M_{\rm{loop}}|^2 {\rm d}s {\rm d}t}{768 \pi^3 m_{\Upsilon(mS)}^3}\,, $

(13)

where the lower and upper limits are given as

$ \begin{split}s_- =& 4m_\pi^2,\\s_+ =& (m_{\Upsilon(mS)}-m_{h_b(nP)})^2,\\ t_{\pm} =& \frac{1}{4s}\Big\{ (m_{\Upsilon(mS)}^2-m_{h_b(nP)}^2)^2\\&-\big[\lambda^{\frac{1}{2}}(s,m_\pi^2,m_\pi^2)\mp \lambda^{\frac{1}{2}}(m_{\Upsilon(mS)}^2,s,m_{h_b(nP)}^2)\big]^2\Big\},\\ \lambda(a,b,c) = & a^2+b^2+c^2-2(ab+ac+bc)\,. \end{split}$

(14)

To estimate the contribution of the $ Z_b $-exchange mechanism, we need to know the coupling strengths of $ Z_{b} \Upsilon(4S)\pi $ and $ Z_{b} h_b(nP)\pi $. The mass difference between $ Z_b(10610) $ and $ Z_b(10650) $ is considerably smaller than the difference between their masses and the $ \Upsilon(mS)\pi/h_b(nP)\pi $ threshold, and they have the same quantum numbers, and thus the same coupling structures as given by Eqs. (1) and (2). Therefore, it is very difficult to distinguish their effects from each other in the dipion transitions of $ \Upsilon(4S) $, so we only used one $ Z_b $, the $ Z_b(10610) $, which approximately combines both $ Z_b $ states' effects. In Ref. [26], we studied the $ \Upsilon(4S) \to \Upsilon(mS)\pi\pi $ processes to extract the coupling constant $ |C_{Z_{b}\Upsilon(4S)\pi}| = (3.3 \pm 0.1)\times 10^{-3} $, which combine the effects from both $ Z_b $ states. For the couplings of $ Z_{b} h_b(nP)\pi $, in principle, they can be extracted from the partial widths of the $ Z_b $ states decay into $ h_b(nP)\pi\,(n = 1,2) $

$ |g_{Z_{b}h_b\pi}| = \Bigg\{\frac{6\pi F_\pi^2 m_{Z_b} \Gamma_{Z_b \to h_b\pi}}{|{{p}}_f|^3 m_{h_b}} \Bigg\}^{\frac{1}{2}} \,, $

(15)

where $ |{{p}}_f|\equiv \lambda^{1/2}\big(m_{Z_b}^2,m_{h_b}^2,m_\pi^2\big)/(2m_{Z_b}) $. The branching fractions of the decays of both $ Z_b $ states into $ h_b(nP)\pi\,(n = 1,2) $ has been given in [40], where the $ Z_b $ line shapes were described using Breit-Wigner forms. If we naively use these branching fractions, we would obtain

$ \begin{split} |g_{Z_{b1}h_b(1P)\pi}^{\rm{naive}}| =& 0.019 \pm 0.003\,, \\ |g_{Z_{b2}h_b(1P)\pi}^{\rm{naive}}| =& 0.021 \pm 0.003\,, \\ |g_{Z_{b1}h_b(2P)\pi}^{\rm{naive}}| =& 0.068 \pm 0.011\,, \\ |g_{Z_{b2}h_b(2P)\pi}^{\rm{naive}}| = &0.077 \pm 0.010\,. \end{split}$

(16)

Here, all the $ Z_{b} h_b\pi $ couplings are labeled by a superscript "naive" because this is not the appropriate way to extract coupling strengths in this case; the $ Z_b $ states are very close to the $ B^{(*)}\bar B^* $ thresholds. Therefore, the Flatté parametrization for the $ Z_b $ spectral functions should be used, which will lead to much larger partial widths into $ (b\bar{b}\pi) $ channels, and thus the relevant coupling strengths. As analyzed in Ref. [41], in the the Flatté parametrization the sum of the partial widths of the $ Z_b(10610) $ other than that for the $ B\bar B^* $ channel should be greater than the nominal width, which is approximately $ 20 \,{\rm{MeV}} $. While summing over all the $ \Upsilon(nS)\pi\,(n = 1,2,3) $ and $ h_b(mP)\pi\,(m = 1,2) $, and the branching fractions in Ref. [40] is approximately 14% or $ 3 \,{\rm{MeV}} $ in terms of partial widths. Therefore, for a rough estimation, we use three times the results of Eq. (16):

$ \begin{split} |g_{Z_{b}h_b(1P)\pi}|\simeq 0.057 \,,\quad |g_{Z_{b}h_b(2P)\pi}|\simeq 0.204 \,. \end{split}$

(17)

We find that even after considering the enlarging factor of three for the couplings $ |g_{Z_{b}h_b(nP)\pi}| $, the $ Z_b $-exchange contribution is still considerably smaller than the bottom meson loops contributions.
In the calculation of the box diagrams, the coupling strength $ g_{JHH(4S)} $ can be extracted from the measured open-bottom decay widths of the $ \Upsilon(4S) $, and we have $ g_{JHH(4S)} = 1.43\pm 0.01 \,{\rm{GeV}}^{-3/2} $. For the $ h_b B^{*}\bar{B}^{*} $ coupling $ g_1 $, we can use the results from Ref. [27]. In [27], the $ Z_b $-exchange mechanism in the $ \Upsilon(5S) \to h_b(1P,2P)\pi\pi $ processes was studied assuming the $ Z_b $ states are $ B^{(\ast)}\bar{B}^{\ast} $ bound states and the physical coupling of the $ Z_b $ states to the bottom and anti-bottom mesons, $ z_1 $, as well as the product $ g_1z_1 $ was determined. By using their results $ z_1 = 0.75^{+0.08}_{-0.11} \,\;{\rm{GeV}}^{-1/2} $ and $ g_1 z_1 = 0.40\pm 0.06 \,\; {\rm{GeV}}^{-1} $, we can extract that $ g_1 = 0.53^{+0.19}_{-0.13} \,\; {\rm{GeV}}^{-1/2} $. In [27], in order to reduce the number of free parameters, the couplings of $ h_b(1P) B^{*}\bar{B}^{*} $ and $ h_b(2P) B^{*}\bar{B}^{*} $ are assumed to be the same.
By using the coupling strengths above, we can predict the decay branching fractions of $ \Upsilon(4S) \to$ $ h_b(1P,2P)\pi^+\pi^- $. Depending on the sign of the couplings in Eq. (17), the interferences can be constructive or destructive between the $ Z_b $-exchange and box graph mechanisms; therefore, there are two possible results for each process

$ \begin{split} & {{BR}}_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-}\simeq \big(1.2^{+0.8}_{-0.4}\times10^{-6}\big) \quad {\rm{or}} \quad \big( 0.5^{+0.5}_{-0.2}\times10^{-6}\big) \,, \\ &{{BR}}_{\Upsilon(4S) \to h_b(2P)\pi^+\pi^-}\simeq \big(7.1^{+1.7}_{-1.1}\times10^{-10}\big) \quad {\rm{or}} \quad\big( 2.4^{+0.2}_{-0.1}\times10^{-10}\big)\,. \end{split}$

(18)

We find that the $ {{BR}}_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-} $ is at least one order of magnitude smaller than the branching fractions $ {{BR}}_{\Upsilon(4S) \to \Upsilon(1S,2S)\pi^+\pi^-} $, which are approximately $ 8\times10^{-5} $ given in PDG [42], and the $ {{BR}}_{\Upsilon(4S) \to h_b(2P)\pi^+\pi^-} $ is small owing to the very small phase space. We discuss the $ \Upsilon(4S) \to h_b(1P)\pi^+\pi^- $ transition in further detail. To illustrate the effects of the $ Z_b $-exchange and box graph mechanisms in $\Upsilon(4S)\to $$ h_b(1P)\pi\pi $, we give the predictions only including the $ Z_b $-exchange terms or only including the box diagrams

$ \begin{split}& {{BR}}_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-}^{Z_b} = 0.6^{+0.1}_{-0.1}\times10^{-7}\,, \\ &{{BR}}_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-}^{\rm{Box}} = 0.8^{+0.7}_{-0.3}\times10^{-6}\,. \end{split}$

(19)

We can observe that the bottom meson loops contribution is considerably larger than the $ Z_b $-exchange contribution, while it is two orders of magnitude smaller than the $\Upsilon(4S) \to $$ \Upsilon(1S,2S)\pi^+\pi^- $ transitions. Note that the direct gluon hadronization mechanism contribution within QCDME for the $ \Upsilon(4S) \to h_b(1P)\pi^+\pi^- $ process has not been calculated thus far. In references [5–8], QCDME predict that the branching fraction of $ \Upsilon(3S) \to h_b(1P) \pi \pi $ is 2-3 orders of magnitude suppressed compared to of $ \Upsilon(3S) \to \Upsilon(1S) \pi \pi $. The three orders of magnitude suppression is supported by experiment [9]. Because the mass difference between the $ \Upsilon(4S) $ and $ h_b(1P) $ is approximately 0.68 GeV, the pions in the $ \Upsilon(4S) \to h_b(1P)\pi^+\pi^- $ process can also be considered to be in the soft region. If one approximates that the gluon hadronization mechanism within QCDME in $ \Upsilon(4S) \to h_b(1P)\pi^+\pi^- $ is also 2-3 orders of magnitudes suppressed compared to that in the $ \Upsilon(4S) \to \Upsilon(1S)\pi^+\pi^- $ process, as in the $ \Upsilon(3S) $ decay cases. Then, the gluon hadronization mechanism contribution is at most at the same order of the bottom meson loops contribution. Owing to the lack of exact information on the gluon hadronization within QCDME and the neglecting of the triangle diagram Fig. 2(a) as discussed in section 2.3, it is important to note that the results presented in this paper are order-of-magnitude estimates.
In Fig. 3, we plot the distributions of the $ \pi\pi $ and $ h_b\pi $ invariant mass spectra, and the distribution of cos$ \theta $, where $ \theta $ is defined as the angle between the initial $ \Upsilon(mS) $ and the $ \pi^+ $ in the rest frame of the $ \pi\pi $ system. To illustrate the effects of different mechanisms, the contributions of the box diagrams, $ Z_b $-exchange, their sum with the constructive interference, and the sum with destructive interference are indicated by dark green dashed, magenta dotted, red solid, and blue dot-dashed lines, respectively. There is a broad bump at approximately 0.5 GeV in the dipion invariant mass distribution. The $ \pi\pi $ invariant mass spectra with unknown normalization predicted within QCDME in Ref. [5] showed a peak at low $ \pi\pi $ masses. Thus, the $ \pi\pi $ invariant mass spectra can be useful to identify the effects of the bottom meson loops and the gluon hadronization mechanism with future experimental data. Further, the angular distribution is far from flat. In the $\Upsilon(mS) \to $$ h_b(nP) \pi \pi $ process, the isospin conservation combined with Bose symmetry requires the pions to have even relative angular momentum. Therefore, there is a large D-wave component from the box diagrams if higher partial waves are neglected.
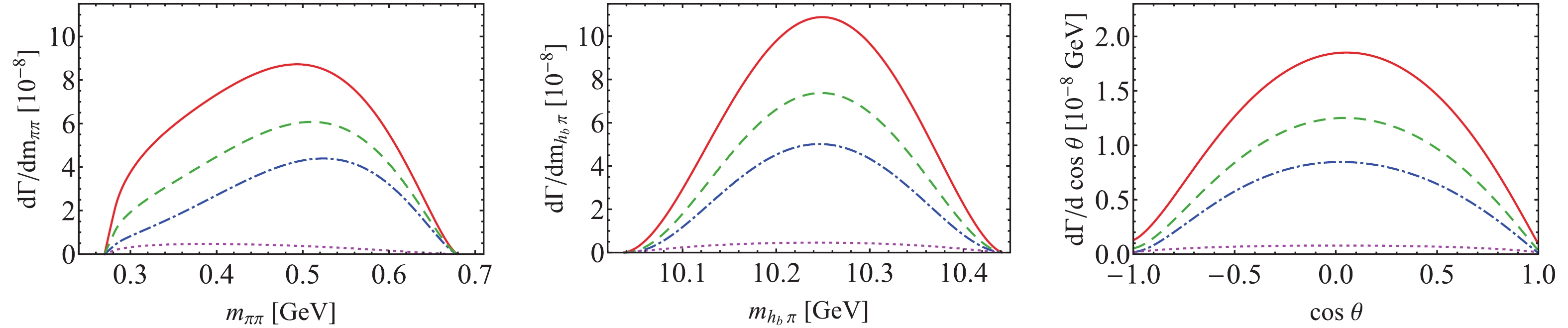Figure3. (color online) Theoretical predictions of the distributions of the $\pi\pi$ and $h_b\pi$ invariant mass spectra, and helicity angular distributions in the $\Upsilon(4S) \to h_b(1P) \pi \pi$ process. Dark green dashed, magenta dotted, red solid, and blue dot-dashed lines represent the contributions of the box diagrams, $Z_b$-exchange, their sum with constructive interference, and the sum with destructive interference, respectively.

The $ \Upsilon(mS) \to h_b(nP)\pi\pi $ are heavy quark spin flip processes, and they are forbidden in the heavy quark limit. We checked that in the heavy quark limit, i.e. $ m_B = m_{B^*} $, all the box diagrams were cancelled with each other; therefore, the bottomed loops did not contribute to the $ \Upsilon(mS)\to h_b(nP)\pi\pi $ transitions. With the small mass splitting of B and $ B^* $ in the real world, as shown in Eqs. (18) and (19), the bottomed meson loops contribution does not produce $ \Upsilon(4S)\to h_b(1P)\pi\pi $ at a rate comparable to the heavy quark spin conserved $ \Upsilon(4S)\to \Upsilon(1S,2S)\pi\pi $ transitions. Note that the datasets collected at $ \Upsilon(4S) $ by BABAR and Belle II collaborations are $ 471\times 10^6 $ and $ 772\times 10^6 $ [43], respectively. Thus, they should contain several hundreds of $ \Upsilon(4S)\to h_b(1P)\pi\pi $ events according to our calculation. We hope future experimental analysis by BABAR and Belle can test our predictions. As stated in the introduction, the observed $ \Upsilon(5S) \rightarrow h_b(nP) \pi^+ \pi^- $ proceed at a rate comparable to the $ \Upsilon(5S) \rightarrow \Upsilon(lS) \pi^+ \pi^- $ processes [10, 11]. The enhancements may be caused by the effects of the on-shell $ Z_b $ exchange and the two-cut condition complexity of the bottom meson loops in the $ \Upsilon(5S) $ decays. A detailed analysis of the $ \Upsilon(5S) \rightarrow $ $h_b(nP) \pi^+ \pi^- $ processes is beyond the scope of this study.
Owing to the similarity between the bottomonium and charmonium families, we can extend the box diagrams calculation to give a rough estimation of the branch fractions of the $ \psi(3S) (\psi(4040)) \to h_c(1P)\pi^+\pi^- $ and $\psi(4S) $$ (\psi(4415)) \to h_c(1P)\pi^+\pi^- $ transitions. The relevant Feynman diagrams can be obtained by replacing the external $ \Upsilon(mS) $ and $ h_b(nP) $ by $ \psi(mS) $ and $ h_c(nP) $, respectively, and replacing the intermediate $ B^{(*)} $ by $ D^{(*)} $ in Fig. 1(b) and (c). The experimental decay widths of the $ \psi(3S,4S) \to D^{(*)}\bar{D}^{(*)} $ transitions are not given in PDG, and we will use the theoretical predictions of the decay widths in Ref. [44] to estimate the coupling strengths $ g_{JHH(\psi(3S))} $ and $ g_{JHH(\psi(4S))} $. Because among the different decay modes $ D^{(*)}\bar{D}^{(*)} $, the $ D\bar{D}^{*} $ and $ D^{*}\bar{D}^{*} $ modes are dominant for $ \psi(3S) $ and $ \psi(4S) $, respectively, we will use the corresponding coupling constants in the calculation, namely $ g_{JHH(\psi(3S))}\!\! =\!\! g_{\psi(3S)D\bar{D}^{*}} \!\!=\!\! 0.97 \;{\rm{GeV}}^{-3/2} $ and $g_{JHH(\psi(4S))}\!\! = \!\!$$ g_{\psi(4S)D^{*}\bar{D}^{*}} = 0.25 \,\;{\rm{GeV}}^{-3/2} $. For the $ h_c D^{*}\bar{D}^{*} $ coupling, we use the result from Ref. [45], $g_{h_c D^{*}\bar{D}^{*}} = -(\sqrt{m_{\chi_{c0}}/3})/(f_{\chi_{c0}}) = $$ -(\sqrt{3.415/3})/(0.297) \,\;{\rm{GeV}}^{-1/2} = -3.59 \,\;{\rm{GeV}}^{-1/2} $. The predictions of the box diagrams contributions to the branch fractions of $ \psi(3S,4S) \to h_c(1P)\pi^+\pi^- $ are

$ \begin{split}& {{BR}}_{\psi(3S) \to h_c(1P)\pi^+\pi^-}^{\rm{Box}} = 2.9\times 10^{-5}\,, \\ &{{BR}}_{\psi(4S) \to h_c(1P)\pi^+\pi^-}^{\rm{Box}} = 4.5\times10^{-3}\,. \end{split} $

(20)

The prediction of $ {{BR}}_{\psi(3S) \to h_c(1P)\pi^+\pi^-}^{\rm{Box}} $ is below the upper limit given in PDG [42]. As expected the branch fractions $ {{BR}}_{\psi(3S,4S) \to h_c(1P)\pi^+\pi^-}^{\rm{Box}} $ are considerably larger than $ {{BR}}_{\Upsilon(4S) \to h_b(1P)\pi^+\pi^-}^{\rm{Box}} $, because the mass splitting of D and $ D^{*} $ is considerably larger than that of B and $ B^{*} $. Note that this is just a preliminary rough estimation, owing to the lack of sufficient information concerning the $ \psi(3S,4S) D^{(*)}\bar{D}^{(*)} $ coupling constants and the neglecting of the loop diagrams with intermediate $ D_1 $ state in the present calculation. A detailed theoretical study of the $ \psi(3S,4S) \to$ $ h_c(1P)\pi^+\pi^- $ transitions will be pursued in the future.

In this study, we investigate the effects of $ Z_b $ exchange and bottom meson loops in the heavy quark spin flip transitions $ \Upsilon(4S) \to h_b(nP)\pi\pi (n = 1, 2) $. The bottom meson loops are treated in the NREFT scheme, in which the dominant box diagrams are considered. We find that the bottom meson loops contribution is considerably larger than the $ Z_b $-exchange contribution in the $\Upsilon(4S) \to $ $ h_b(1P)\pi\pi $ transition, while it can not produce decay rates comparable to the heavy quark spin conserved $ \Upsilon(4S) \to \Upsilon(1S,2S)\pi\pi $ processes. The theoretical prediction of the decay rate and the dipion invariant mass spectra of $ \Upsilon(4S) \to h_b(1P)\pi\pi $ in this work may be useful for identifying the effect of the bottom meson loops with future experimental analysis. We also predict the branch fractions of $ \psi(3S,4S) \to h_c(1P)\pi\pi $ contributed from the charm meson loops.

In this appendix, first, we discuss the parametrization and simplification of the scalar four-point integrals in the box diagrams. Then, we introduce a tensor reduction scheme to deal with higher-rank loop integrals. Finally, we give the amplitude of the box diagrams for the $ \Upsilon(mS) \to h_b(nP)\pi\pi $ process.
2

-->

A.1.Scalar four-point integrals

For the first topology, as shown in Fig. A1, the scalar integral evaluated for the initial bottomonium at rest ($ p = (M, {\bf{0}}) $) reads
FigureA1. Kinematics used for calculating four-point integrals.

We are grateful to the referees' useful suggestions and constructive remarks, which helped formulate the present version of this manuscript. We are grateful to Martin Cleven for the collaboration in the early stages of this study. We acknowledge Guo-Ying Chen, Meng-Lin Du, and Qian Wang for their helpful discussions, and Feng-Kun Guo for a careful reading of the manuscript and valuable comments.

$\tag{A1} \begin{split} J_1^{(0)} \equiv & {\rm i}\int \!\frac{{\rm d}^4l}{(2\pi)^4}\frac{1}{[l^2-m_1^2+{\rm i}\epsilon][(p-l)^2-m_2^2+{\rm i}\epsilon][(l-q_1-q_2)^2-m_3^2+i\epsilon][(l-q_1)^2-m_4^2+{\rm i}\epsilon]}\simeq\frac{-{\rm i}}{16m_1m_2m_3m_4}\\ &\times \int \! \frac{{\rm d}^4l}{(2\pi)^4} \frac{1}{\left[l^0-\frac{{{l}}^2}{2m_1}-m_1+{\rm i}\epsilon\right]\left[l^0-M+\frac{{{l}}^2}{2m_2}+m_2-{\rm i}\epsilon\right]} \frac{1}{\left[l^0-q_1^0-q_2^0-\frac{({\bf{l}}+{{q}})^2}{2m_3}-m_3+{\rm i}\epsilon\right]\left[l^0-q_1^0-\frac{({\bf{l}}-{{{q}}_1})^2}{2m_4}-m_4+{\rm i}\epsilon\right]} . \end{split} $

By performing the contour integration, we find

$\tag{A2} -\frac{\mu_{12}\mu_{23}\mu_{24}}{2m_1m_2m_3m_4}\int \! \frac{{\rm d}^3l}{(2\pi)^3}\frac{1}{ [{{l}}^2+c_{12}-{\rm i}\epsilon][{{l}}^2+2\frac{\mu_{23}}{m_3}{{l}}\cdot {{q}}+c_{23}-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{24}}{m_4}{{l}}\cdot {{q}}_1+c_{24}-{\rm i}\epsilon]} , $

where we defined

$ \tag{A3}\begin{split} c_{12} \equiv & 2\mu_{12}\left(m_1+m_2-M\right), \quad c_{23}\equiv 2\mu_{23}\left(m_2+m_3-M+q_1^0+q_2^0+\frac{ {{q}}^2}{2m_3}\right), \\ c_{24} \equiv & 2\mu_{24}\left(m_2+m_4-M+q^0_1+\frac{ {{q}}_1^2}{2m_4}\right), \quad \mu_{ij} = \frac{m_im_j}{m_i+m_j}. \end{split} $

The second topology in Fig. A1 is just the crossed diagram of the first topology with $ q_1 \leftrightarrow q_2 $, so the scalar integral reads

$\tag{A4}\begin{split} J_2^{(0)} =& -\frac{\mu_{12}\mu_{23}\mu_{24}}{2m_1m_2m_3m_4} \int \frac{{\rm d}^3l}{(2\pi)^3}\\&\times\frac{1}{ [{{l}}^2+c_{12}-{\rm i}\epsilon][{{l}}^2+2\frac{\mu_{23}}{m_3}{{l}}\cdot {{q}}+c_{23}-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{24}}{m_4}{{l}}\cdot {{q}}_2+c_{24}^\prime-{\rm i}\epsilon]} , \end{split}$

where

$ \tag{A5} c_{24}^\prime \equiv 2\mu_{24}\left(m_2+m_4-M+q^0_2+\frac{ {{q}}_2^2}{2m_4}\right)\,. $

For the third topology, we have

$\tag{A6}\begin{split} J_3^{(0)} \equiv& {\rm i}\int \!\frac{{\rm d}^4l}{(2\pi)^4}\frac{1}{[l^2-m_1^2+{\rm i}\epsilon][(p-l)^2-m_2^2+{\rm i}\epsilon][(p-q_2-l)^2-m_3^2+{\rm i}\epsilon][(l-q_1)^2-m_4^2+{\rm i}\epsilon]}\\ \simeq &\frac{-{\rm i}}{16m_1m_2m_3m_4}\int \! \frac{{\rm d}^4l}{(2\pi)^4} \frac{1}{\left[l^0-\frac{{{l}}^2}{2m_1}-m_1+{\rm i}\epsilon\right]\left[l^0-M+\frac{{{l}}^2}{2m_2}+m_2-{\rm i}\epsilon\right]}\times \frac{1}{\left[l^0+q_2^0-M+\frac{({\bf{l}}+{{{q}}_2})^2}{2m_3}+m_3-{\rm i}\epsilon\right]\left[l^0-q_1^0-\frac{({\bf{l}}-{{{q}}_1})^2}{2m_4}-m_4+{\rm i}\epsilon\right]}. \end{split} $

By the contour integration, we find

$\tag{A7} \begin{split} -\frac{\mu_{12}\mu_{34}}{2m_1m_2m_3m_4}\int \! \frac{{\rm d}^3l}{(2\pi)^3}\frac{1}{ [{{l}}^2+d_{12}-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{34}}{m_4}{{l}}\cdot {{{q}}_1}-2\frac{\mu_{34}}{m_3}{{l}}\cdot {{{q}}_2}+d_{34}-{\rm {\rm i}}\epsilon]}\times\left[\frac{\mu_{24}}{[{\bf{l}}^2-2\frac{\mu_{24}}{m_4}{{l}}\cdot {{q}}_1+d_{24}-{\rm i}\epsilon]}+\frac{\mu_{13}}{[{{l}}^2+2\frac{\mu_{13}}{m_3}{{l}}\cdot {{q}}_2+d_{13}-{\rm i}\epsilon]} \right], \end{split}$

where we defined

$\tag{A8}\begin{split}d_{12}\equiv {2\mu_{12}\left(m_1+m_2-M\right),}\;\;\;\;\;{d_{34}\equiv 2\mu_{34}\left(m_3+m_4-q^0+\frac{ {{q}}_1^2}{2m_4}+\frac{ {{q}}_2^2}{2m_3}\right),}\;\;\;d_{24}\equiv { 2\mu_{24}\left(m_2+m_4-M+q_1^0+\frac{ {{q}}_1^2}{2m_4}\right),}\;\;\;{d_{13}\equiv 2\mu_{13}\left(m_1+m_3-M+q_2^0+\frac{ {{q}}_2^2}{2m_3}\right). }\end{split}$

In all the three cases, the remaining three-dimensional momentum integration will be carried out numerically.
2 -->

A.2.Tensor reduction

Because the $ \Upsilon B^{(*)}\bar{B}^{(*)} $ vertex scales with the momentum of the bottom meson pair, for topology I we have to deal with

$\tag{A9} \frac{-\mu_{12}\mu_{23}\mu_{24}}{2m_1m_2m_3m_4}\int \! \frac{{\rm d}^3l}{(2\pi)^3}\frac{f(l)}{ [{{l}}^2+c_{12}-{\rm i}\epsilon][{{l}}^2+2\frac{\mu_{23}}{m_3}{{l}}\cdot {{q}}+c_{23}-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{24}}{m_4}{{l}}\cdot {{{q}}_1}+c_{24}-{\rm i}\epsilon]}, $

where $ f(l) = \{1,\, l^i\} $ for the fundamental scalar and vector integrals, respectively. A convenient parametrization of the tensor reduction is

$ \tag{A10} J_1^{(1)i} = \frac{-\mu_{12}\mu_{23}\mu_{24}}{2m_1m_2m_3m_4}\int \! \frac{{\rm d}^3l}{(2\pi)^3}\frac{l^i}{[{{l}}^2+c_1-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{23}}{m_3}{{l}}\cdot {{q}}+c_2-{\rm i}\epsilon][{{l}}^2-2\frac{\mu_{24}}{m_4}{{l}}\cdot {{q}}_1+c_3-{\rm i}\epsilon]} \equiv q^iJ_1^{(1)}+q_{1\perp}^iJ_1^{(2)}\,, $

where $ {{q}}_{1\perp} = {{{q}}_1}-{{q}}({{q}}\cdot {{{q}}_1})/{{q}}^2 $. The expressions of the scalar integrals $ J^{(r)}_1 $ can easily be disentangled and should be evaluated numerically. The corresponding expressions for topology II and III can be obtained by changing the denominators accordingly.
2 -->

A.3.Amplitudes

We define the scalar integrals $ J1(i, r, k) $ based on the $ J_1^{(r)} $ in the tensor reduction of vector integral in Eq. (A10), where $ i = 1, 2, 3 $ denotes the three topologies of the box diagrams shown in Fig. A1, $ r = 1, 2 $ refers to the two components $ J_1^{(r)} $, and $ k = 1, 2,...,12 $ represents the twelve patterns with different pseudoscalar or vector content of the intermediate bottom mesons in $ [M1,\; M2,\; M3,\; M4] $ as displayed in Sec. 2.3.
We give the amplitude of the box diagrams for the $ \Upsilon(mS) \to h_b(nP)\pi\pi $ process, namely the $ A_l (l = 1,2,...,6) $ in the Eq. (12).

$\tag{A11}\begin{split} A_1 = &\frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2 {{q}}^2} \bigg\{ {{q}}^2 \Big\{{{{p}}_c}\cdot {{{p}}_d} \big[J1(1,1,3)+J1(2,1,3)+J1(3,1,8)\big]+{{{p}}_c}\cdot {{q}} \big[J1(1,1,9)+J1(1,1,11) -J1(2,1,12)+J1(3,1,9)+J1(3,1,11)\big]+ {{q}}_\perp^2 \big[J1(1,2,9)\\&+J1(1,2,11)-J1(2,2,12)+J1(3,2,9) +J1(3,2,11)\big]\Big\}+{{{p}}_c}\cdot {{q}} \Big\{{{{p}}_c}\cdot {{q}} \big[J1(1,1,9)+J1(1,1,11)-J1(2,1,12)+J1(3,1,9)+J1(3,1,11)\big] \\&+{{{p}}_d}\cdot {{q}} \big[J1(1,1,12)-J1(2,1,9)-J1(2,1,11)+J1(3,1,10)\big]+ {{q}}_\perp^2 \big[J1(1,2,9)+J1(1,2,11) -J1(1,2,12)+J1(2,2,9)+J1(2,2,11)-J1(2,2,12)\\&+J1(3,2,9)-J1(3,2,10)+J1(3,2,11)\big]\Big\}\bigg\}\,, \end{split}$

$\tag{A12}\begin{split} A_2 =& \frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2} \Big\{{{{p}}_c}\cdot {{{p}}_d} \big[J1(1,2,3)+J1(2,2,3)+J1(3,2,8)\big]+{{{p}}_c}\cdot {{q}} \big[J1(1,1,9)+J1(1,1,11) -J1(2,1,12)+J1(3,1,9)+J1(3,1,11)\big]\\&+{{{p}}_d}\cdot {{q}} \big[J1(1,1,12)-J1(2,1,9)-J1(2,1,11) +J1(3,1,10)\big]+ {{q}}_\perp^2\big[J1(1,2,9)+J1(1,2,11)-J1(1,2,12)+J1(2,2,9)\\&+J1(2,2,11) -J1(2,2,12)+J1(3,2,9)-J1(3,2,10)+J1(3,2,11)\big]\Big\}\,, \end{split}$

$\tag{A13}\begin{split} A_3 =& -\frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2 {{q}}^2} \Big\{ {{q}}^2 \big[-J1(1,1,9)+J1(1,1,11)-J1(1,1,12)-J1(1,2,2)+J1(1,2,9)+J1(1,2,10) +J1(1,2,12)-J1 (2,1,9)+J1(2,1,11)-J1(2,1,12)\\&+J1(2,2,2)-J1(2,2,10)-J1(2,2,11) -J1(3,1,9)-J1(3,1,10)+J1(3,1,11)-J1(3,2,2)+J1(3,2,9)+J1(3,2,10)+J1 (3,2,12)\big] \\&+{{{p}}_c}\cdot {{q}} \big[J1(1,2,9)-J1(1,2,11)+J1(1,2,12)+J1(2,2,9)-J1(2,2,11)+J1(2,2,12) +J1(3,2,9)+J1(3,2,10)-J1(3,2,11)\big]\Big\}\,, \end{split}$

$\tag{A14}\begin{split} A_4 =& \frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2 {{q}}^4} \Big\{ {{q}}^4 \big[J1(1,1,2)-J1(1,1,10)-J1(1,1,11)-J1(2,1,2)+J1(2,1,9)+J1(2,1,10) +J1(2,1,12)+J1 (3,1,2)-J1(3,1,11)-J1(3,1,12)\big]\\&+ {{q}}^2 {{{p}}_c}\cdot {{q}} \big[J1(1,1,9)-J1(1,1,11) +J1(1,1,12)-J1(1,2,9)+J1(1,2,11)-J1(1,2,12)+J1 (2,1,9)-J1(2,1,11)+J1(2,1,12) -J1(2,2,9)\\&+J1(2,2,11)-J1(2,2,12)+J1(3,1,9)+J1(3,1,10)-J1(3,1,11)-J1(3,2,9) -J1(3,2,10)+J1(3,2,11)\big)- ({{{p}}_c}\cdot {{q}})^2 \big[J1(1,2,9)-J1(1,2,11)\\&+J1(1,2,12)+J1(2,2,9) -J1(2,2,11)+J1(2,2,12)+J1(3,2,9)+J1(3,2,10)-J1(3,2,11)\big]\Big\}\,, \end{split}$

$\tag{A15}\begin{split} A_5 =& \frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2 {{q}}^2} \Big\{ {{q}}^2 \big[-J1(1,1,6)+J1(1,2,8)+J1(1,2,10)-J1(2,1,6)+J1(2,2,6)-J1(2,2,8) -J1(2,2,10)-J1 (3,1,3)\\&+J1(3,1,6)-J1(3,1,8)+J1(3,2,3)+J1(3,2,12)\big]+{{{p}}_c}\cdot {{q}} \big[J1(1,2,6)+J1(2,2,6)+J1(3,2,3)-J1(3,2,6)+J1(3,2,8)\big]\Big\}\,, \end{split}$

$\tag{A16}\begin{split} A_6 =& -\frac{8 g_1 g_{JHH}g_\pi^2}{F_\pi^2 {{q}}^4} \Big\{ {{q}}^4 \big[J1(1,1,6)-J1(1,1,8)-J1(1,1,10)+J1(2,1,8)+J1(2,1,10)-J1(3,1,6) +J1(3,1,8)-J1 (3,1,12)\big]\\&+ {{q}}^2 {{{p}}_c}\cdot {{q}} \big[J1(1,1,6)-J1(1,2,6)+J1(2,1,6)-J1(2,2,6)+J1(3,1,3) -J1(3,1,6)+J1(3,1,8)-J1(3,2,3)+J1 (3,2,6)-J1(3,2,8)\big]\\&-({{{p}}_c}\cdot {{q}})^2 \big[J1(1,2,6)+J1(2,2,6) +J1(3,2,3)-J1(3,2,6)+J1(3,2,8)\big]\Big\}\,. \end{split} $