Jun Su
, Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China
Received Date:2019-02-08
Available Online:2019-06-01
Abstract:In our previous study, the deduced Langevin equation has been applied to investigate the isoscalar giant monopole resonance. In the current study, the framework is extended to study the isovector giant dipole resonance (IVGDR). The potential well in the IVGDR is calculated by separating the neutron and proton densities based on the Hartree-Fock ground state. Subsequently, the Langevin equation is solved self-consistently, resulting in the centroid energy of the IVGDR without width. The symmetry energy around the density of 0.02 fm^?3 contributes the most to the potential well in the IVGDR. By comparison with the updated experimental data of IVGDR energies in spherical nuclei, the calculations within 37 sets of Skyrme functionals suggest the symmetry energy to be in the range of 8.13-9.54 MeV at a density of 0.02 fm^?3.

HTML

--> --> -->

The nuclear giant resonances are the phenomena that arise from the high-frequency collective motion of a strongly interacting nuclear system. These resonances have been the object of theoretical and experimental research in modern nuclear physics over the last decades, since they play a crucial role in the understanding of nonequilibrium properties of nuclei and the nuclear force [1–4]. The first observation of the giant resonance can be traced back to 1947, when Baldwin and Klaiber measured the $ \gamma $ spectrum in photonuclear reactions [5]. This was referred to as the isovector giant dipole resonances (IVGDR), which is microscopically described as the coherent excitation of particle-hole configurations across one major shell, and macroscopically considered as the quantized oscillation of neutron and proton densities in anti-phase. After about 40 years later, the isoscalar giant quadrupole and monopole resonances were also observed by proton and $ \alpha $ scattering experiments on nuclei [6, 7].
Because of its proven measurement technique and strong relation to the microscopic structure of the nuclei, the IVGDR has been employed as an excellent probe for determination of nuclear properties, such as the fission hindrance [8], nuclear deformation at finite excitation [9], clustering configurations [10], isospin mixing at high temperature [11], and shear viscosity to entropy density ratio [12]. The relationship between the symmetry energy and the IVGDR has been efficiently described by some models, such as the hydrodynamical model [13], isospin-dependent quantum molecular dynamics model [14], and isospin-dependent Boltzmann-Uehling-Uhlenbeck model [15]. The experimental value of the IVGDR, such as in ²⁰⁸Pb, has been used as a constraint on the symmetry energy at subnormal densities [16].
The symmetry energy is defined by the parabolic approximation of the total energy per nucleon of the isospin asymmetry nuclear matter, $ E(\rho, \delta) = E(\rho, 0) + E_{\rm sym}(\rho)\delta^{2} +$$ \mathcal{O}(\delta^{4}) $, where $ \delta = (\rho_{n}-\rho_{p})/(\rho_{n}+\rho_{p}) $ is the isospin asymmetry, and E_sym is the symmetry energy [17, 18]. The symmetry energy at normal density $ \rho_{0} $ = 0.16 fm^?3 has been studied from the properties of the nuclei in the ground state [19]. Many efforts were made to constrain the symmetry energy at subnormal densities, for example around 0.25$ \rho_{0} $ to understand the supernova [20], and in the region of 0.5 < $ \rho $/$ \rho_{0} $ < 0.7 to study the boundary in neutron stars [21, 22] and crustal vibrations in Magnetars [23]. The analyses of experimental data have generated a constraint at subnormal densities [24, 25]. However, the experimental determination of the symmetry energy is dependent on the reliability of the model. Further studies are needed to improve the accuracy of the constraint on the symmetry energy at subnormal densities.
In this study, we attempt to constrain the symmetry energy at the subnormal density by the IVGDR data of the spherical nuclei. This idea is not new, but in the present work we develop it based on the global IVGDR data and a new theoretical framework. In the recent publication [26], the updated experimental data and corresponding uncertainties of IVGDR energies are presented. We use these global data, rather than only the data of one or several nuclei. Moreover, we use the theoretical framework based on the Skyrme energy-density functional and the Langevin equation, which has been successfully applied to study the isoscalar giant monopole resonances (ISGMR) in our previous work [27]. The paper is organized as follows. In Sec. 2, we describe the method. In Sec. 3, we present both the results and discussions. Finally, the summaries are given in Sec. 4.

The fluid dynamical reduction of the Boltzmann-Langevin equation was carried out for a situation where the velocity field can be described by a set of N collective variables [28]. A set of N coupled Langevin equations is obtained for the collective variables, which constitute a generalization of the Bohr-Mottelson model for the hot nuclei. For the IVGDR, the collective variable X is the distance of the centres between the neutrons and the protons, resulting in the Langevin equation [29],

$M\ddot X + \frac{{\partial V}}{{\partial X}} = D(t) + \delta F(t),$

(1)

where M = mNZ/A represents the collective mass of the neutron-proton relative motion, V is the potential energy, D(t) is the force related to the damping, and $ \delta F(t) $ is the random force. The centroid energy is independent of the damping and the random force. Hence D(t) and $ \delta F(t) $ are not considered in the calculations. The potential energy is the sum of the Coulomb and nuclear Skyrme energies, the density dependence of which is given in our previous work [27]. The nuclear Skyrme energy can be written as a sum of the two-body term V₀, three-body term V₃, effective mass term V_eff, finite-range term V_fin, spin-orbit term V_so, and tensor coupling term V_sg [30, 31]:

$\begin{split}V =& {V_0} + {V_3} + {V_{\rm eff}} + {V_{\rm fin}} + {V_{\rm so}} + {V_{\rm sg}}\\ =& \int {{\rm d^3}} {{r}}({\varepsilon _0} + {\varepsilon _3} + {\varepsilon _{\rm eff}} + {\varepsilon _{\rm fin}} + {\varepsilon _{\rm so}} + {\varepsilon _{\rm sg}}),\\{\varepsilon _0} =& \frac{{{t_0}}}{2}\left(1 + \frac{{{x_0}}}{2}\right){\rho ^2} - \frac{{{t_0}}}{2}\left({x_0} + \frac{1}{2}\right)\left(\rho _n^2 + \rho _p^2\right),\\{\varepsilon _3} = &\frac{{{t_3}}}{{12}}\left(1 + \frac{{{x_3}}}{2}\right){\rho ^{\sigma + 2}} - \frac{{{t_3}}}{{12}}\left({x_3} + \frac{1}{2}\right){\rho ^\sigma }\left(\rho _n^2 + \rho _p^2\right),\\\end{split}$

$\begin{split}{\varepsilon _{\rm eff}} =& \frac{1}{4}\left[{t_1}\left(1 + \frac{{{x_1}}}{2}\right) + {t_2}\left(1 + \frac{{{x_2}}}{2}\right)\right]\rho ({\tau _n} + {\tau _p})\\ &+ \frac{1}{4}\left[{t_2}\left({x_2} + \frac{1}{2}\right) - {t_1}\left({x_1} + \frac{1}{2}\right)\right]({\rho _n}{\tau _n} + {\rho _p}{\tau _p}),\\{\varepsilon _{\rm fin}} =& \frac{1}{{16}}\left[3{t_1}\left(1 + \frac{{{x_1}}}{2}\right) - {t_2}\left(1 + \frac{{{x_2}}}{2}\right)\right]{(\nabla \rho )^2}\\ &- \frac{1}{{16}}\left[3{t_1}\left({x_1} + \frac{1}{2}\right) + {t_2}\left({x_2} + \frac{1}{2}\right)\right]\left[{\left(\nabla {\rho _n}\right)^2} + {\left(\nabla {\rho _p}\right)^2}\right],\\{\varepsilon _{\rm so}} =& \frac{1}{2}{W_0}[{{J}} \cdot \nabla \rho + {{{J}}_n} \cdot \nabla {\rho _n} + {{{J}}_p} \cdot \nabla {\rho _p}],\\{\varepsilon _{\rm sg}} = & - \frac{1}{{16}}({t_1}{x_1} + {t_2}{x_2}){J^2} + \frac{1}{{16}}({t_1} - {t_2})(J_n^2 + J_p^2),\end{split}$

(2)

where $ \rho $, $ \tau $, and J are the local nucleon density, kinetic energy density, and spin density, respectively. The subscripts n and p represent the neutron proton, respectively.
The density distribution of the static Hartree-Fock ground state is determined by the Skyrme Hartree-Fock-Bogolyubov (SHFB) model within the spherical symmetry, the code of which is given in Ref. [32].
Subsequently, the potential energy is calculated as a function of the collective variable X after separating the centers between the neutron and the proton densities. The results for ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb are shown in Fig. 1. Because the Fermi kinetic energy is independent of the collective variable X, the potential energy and the energy per nucleon exhibit the same potential well. We observe the harmonic-oscillator-type potential well. The valley values represent binding energies of the nuclei, which will not affect the excitation energy of the IVGDR. The widths of the potential wells exhibit a mass dependence, which is the origin of the mass dependence of the IVGDR energy.
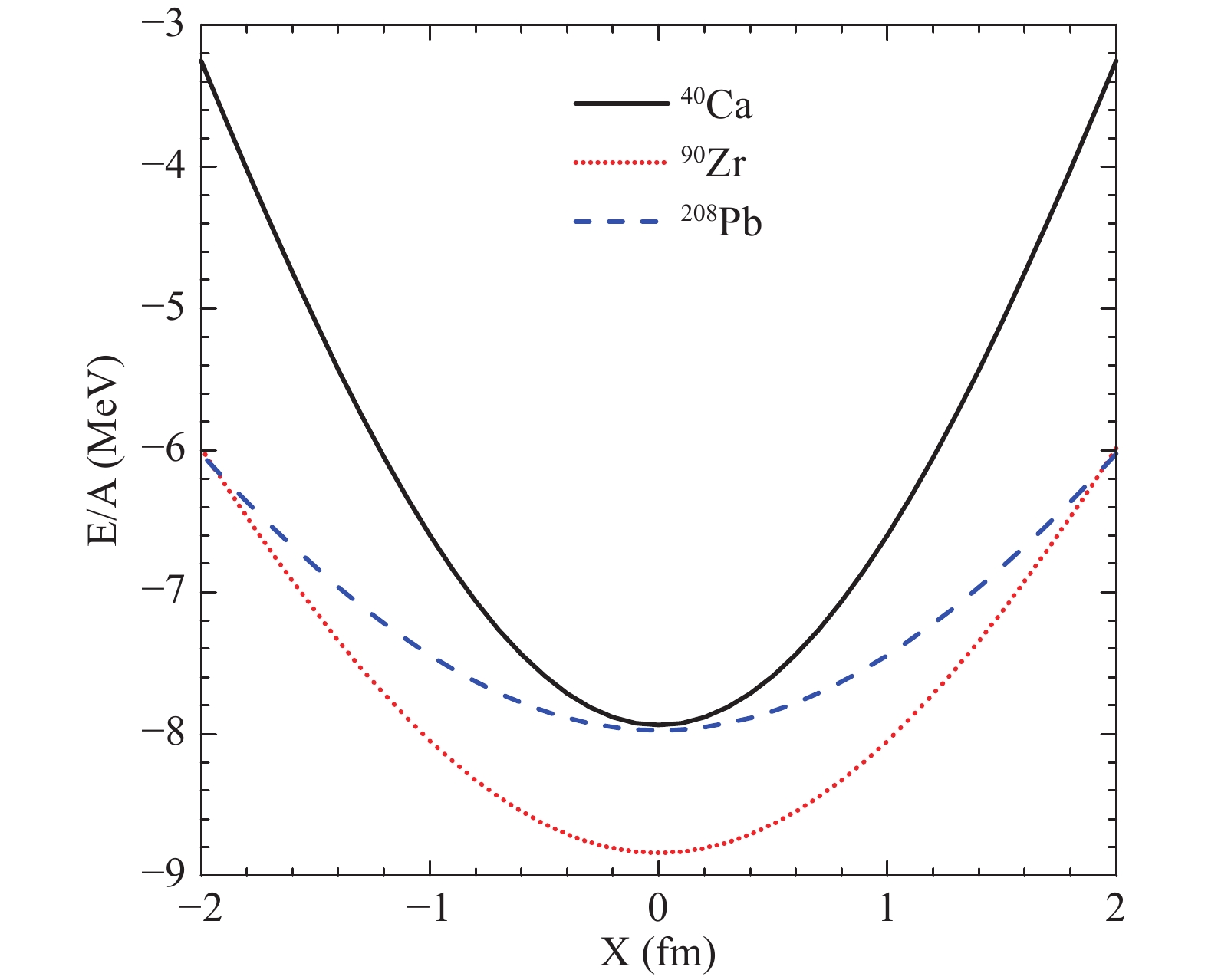Figure1. (color online) Energy per nucleon as a function of the collective variable X in the IVGDR of ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb.

With the potential energy as a function of the collective variable X, the Langevin equation Eq. (1) can be solved self-consistently. The initial value X₀ of the collective variable is zero. The initial velocity $ \dot{X}_{0} $ depends on the input IVGDR energy $E^* $,

${\dot X_0} = \sqrt {\frac{{2{E^*}}}{M}} .$

(3)

The solution of Eq. (1) with initial conditions exhibits an oscillation structure. The Fourier transform of the solution provides the frequency of the spectrum $ \omega $, and subsequently the output IVGDR energy $ E^{*}_{\rm out} = \hbar \omega $. The Langevin equation is solved again using the initial velocity depending on the output energy, unless the difference between the input and output IVGDR energies is less than an infinitesimal amount (e.g., 0.001 MeV).
Figure 2 shows the solution of the Langevin equation for ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb nuclei. In the calculation, the BSk9 functional is applied. The solutions exhibit a good oscillation structure. Due to the narrowest potential well, the period for the ⁴⁰Ca nucleus is the shortest. With the Fourier transform, one obtains the excitation energy 18.44 MeV from the period value 59.8 fm/c. Compared with the data 20.14 ± 1.01 [33], the excitation energy is smaller by 8.4%. The period for the ⁹⁰Zr nucleus is 75.4 fm/c, resulting in $ E^*$ (⁹⁰Zr) = 16.44 MeV. Within the experimental error, the calculation agrees to the data 16.9 ± 0.84 [34]. For the ²⁰⁸Pb nucleus, the calculation of the excitation energy 13.90 MeV is very close to the data 13.34 ± 0.40 [34].
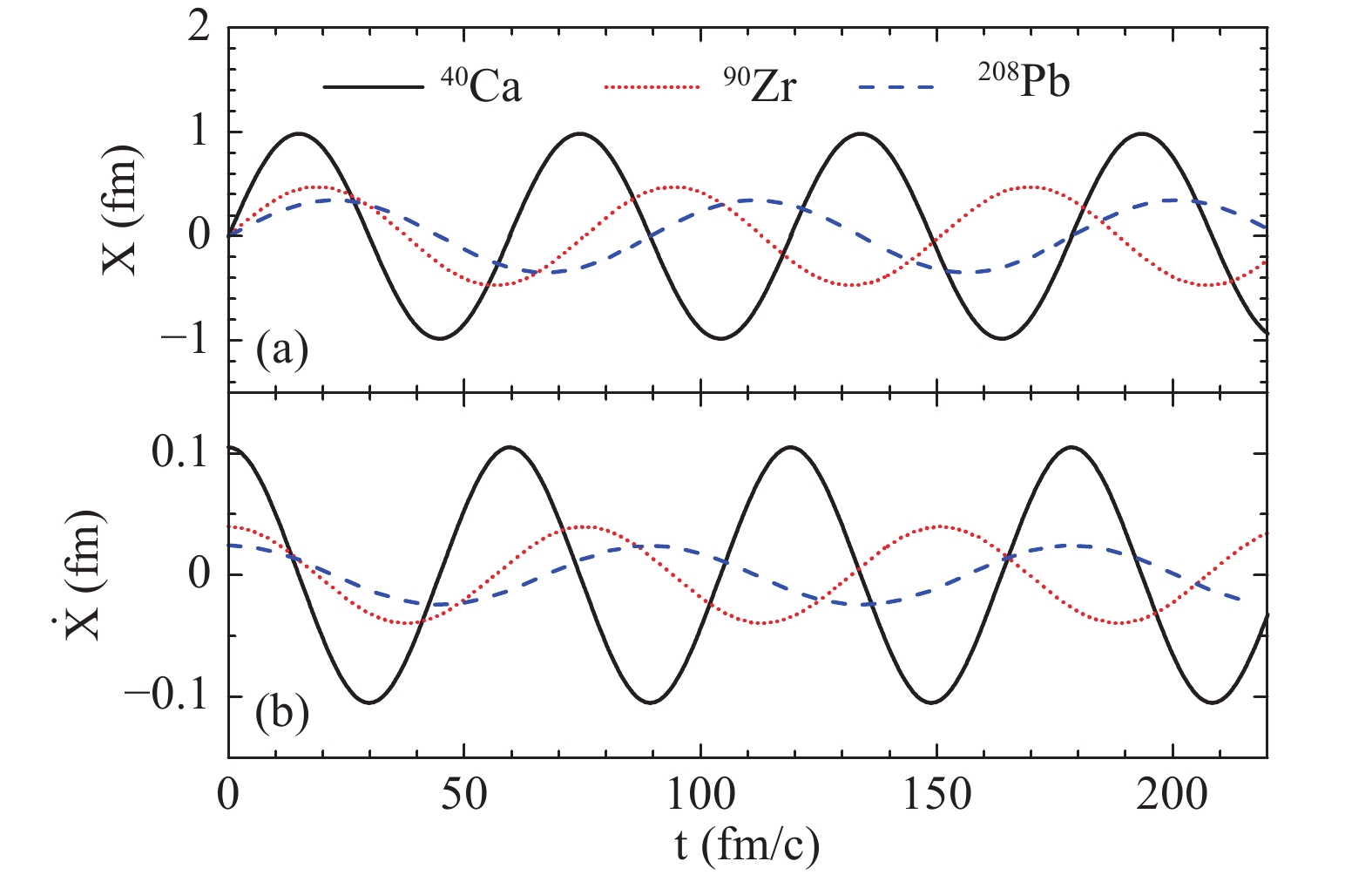Figure2. (color online) Solutions of Eq. (1), shown as (a) the collective variable X and (b) the velocity $ \dot{X}_{0} $ as a function of time for ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb nuclei.

Recently, the updated experimental data and corresponding uncertainties of IVGDR energies were presented [26]. We attempt to use these data to probe the symmetry energy. Since the SHFB code within the spherical symmetry is applied, the data for the spherical nuclei, shown as a function of the mass number in Fig. 3, will be considered. A set of 37 Skyrme functionals is applied to perform the calculation. These are BSk1, BSk6, BSk7, BSk8, BSk9, MSk2, MSk4, MSk5, MSk6, MSk7, MSk8, MSL0, SkMP, SkS2, SKz1, SKz2, SKz3, SKz4, SLy0, SLy1, SLy10, SLy2, SLy230a, Sly230b, SLy3, SLy4, SLy5, SLy6, SLy7, SLy8, SLy9, v075, v080, v090, v100, v105, and v110. The nuclear incompressibility provided by these Skyrme functionals is about 230 MeV, which is the value constrained by the ISGMR data. As examples, the calculations within the functionals Skz4, BSk9, and SkMP are shown in Fig. 3. The slope of the symmetry energy at normal density is 5.75, 38.29, and 70.31 MeV for Skz4, BSk9, and SkMP functionals, respectively. By comparing the calculations within these three functionals, one may conclude that the IVGDR energies depend strongly on the slope parameter of the symmetry energy. However, after analyzing the calculations within the set of 37 Skyrme functionals, we fail to find a good correlation between the IVGDR energies and the slope parameter of the symmetry energy. This phenomenon may cause an appreciable error when constraining the properties of the symmetry energy, as in the study of Ref. [15]. In another reference, the IVGDR is considered as a quantitative constraint on the symmetry energy around 0.1 fm^?3 [13].
Figure3. (color online) Excitation energies of the IVGDR as a function of the mass number for spherical nuclei. In the calculation, the functionals Skz4, BSk9, and SkMP are applied, consecutively. The solid line shows the fit by the A^-1/3 law. Experimental data are obtained from Ref. [26].

Figure 2 shows that the amplitudes of the IVGDR are 0.98, 0.47, and 0.35 fm for ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb respectively. This means that only the skins of the neutrons and protons, in which the density is in the subnormal region, are separated in the resonances. Figure 4(a) shows the density distribution of the static Hartree-Fock ground state of ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb nuclei. The thicknesses of the skins are less than 2 fm, which is less than the amplitudes of the IVGDR. Figure 4(b) shows the difference of the isospin asymmetry between the ground state and the IVGDR state for X = 0.1, 0.2, 0.3, and 0.4 fm. Only the isospin asymmetry in the skin exhibits a great change in the IVGDR. Moreover, the cures have peaks near 0.02 fm^?3. The symmetry energy at density 0.02 fm^?3 indicates the highest contribution to the potential well.
Figure4. (color online) (a) Density distribution of the static Hartree-Fock ground state of ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb nuclei. (b) Difference of the isospin asymmetry between the ground state and the IVGDR state for the collective variable X = 0.1, 0.2, 0.3, and 0.4 fm. The amplitude increases from X = 0.1 fm to 0.4 fm, which is marked for ⁴⁰Ca.

We use two observables to describe the agreement of the calculations to the data. One is the mean square deviation (MSD), and the other is the scale parameter. The MSD is defined as,

${\rm MSD} = \frac{1}{N}\sum\limits_i^N {\frac{{{{(E_{{\rm cal},i}^* - E_{{\rm exp},i}^*)}^2}}}{{\sigma _{{\rm exp},i}^2}}} ,$

(4)

where N is the number of the nuclei whose data is available, $ E^{*}_{{\rm cal},i} $ is the calculated IVGDR energy, $ E^{*}_{{\rm exp},i} $ is the experimental IVGDR energy, and $ \sigma_{{\rm exp},i} $ is the error of the data. In order to consider the contribution of each data according to the uncertainties, the factor 1/$ \sigma_{{\rm exp}}^{2} $ is included. The MSD for each functional, as a function of the symmetry energy at density 0.02 fm^?3, is shown in Fig. 5 (a). The MSD definitely rules out both very small and very large symmetry energy at subnormal density. The functionals MSk2 and SLy230a are suggested according to the smallest values of MSD. They have a symmetry energy of 8.13 MeV and 9.54 MeV at a density of 0.02 fm^?3.
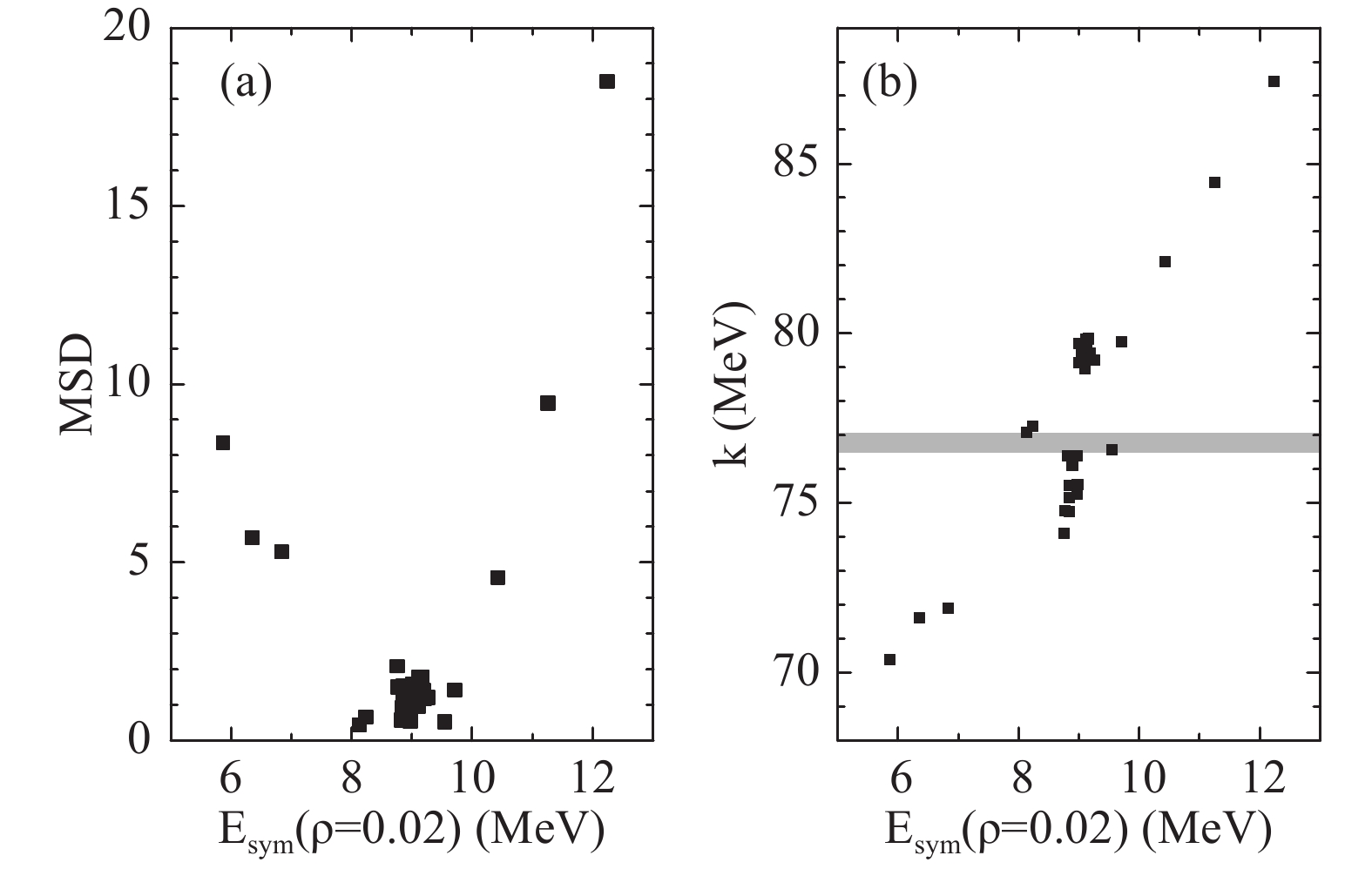Figure5. (a) Mean square deviation of the calculation compared with the data, and (b) scale parameter, shown as a function of the symmetry energy at density 0.02 fm^?3 provided by the Skyrme functionals.

The IVGDR energy decreases with increasing mass, which can be described by the scale law kA^?1/3. Fitting the data, we obtain k = 76.78 ± 0.28. For the calculations, the scale parameters increase linearly with increasing symmetry energy at a density 0.02 fm^?3, as shown in Fig. 5(b). The scale parameters for the functionals MSk2 and SLy230a denote the upper and lower limits of the data range, respectively. The symmetry energy at the density of 0.02 fm^?3 is in the region 8.13 MeV to 9.54 MeV. Many studies dealt with the symmetry energy at subnormal densities, as described in the review articles Ref. [24]. At the density of 0.02 fm^?3, the symmetry energy from 6.4 MeV to 8.2 MeV is recommend by the best fitted to the masses of double magic nuclei [35]. This recommended region is slightly smaller than our suggested region, although they overlap. Another symmetry energy of 8.8 MeV, suggested by the chiral effective field calculations, is in the center of our suggested region [36].

The fluid dynamics reduction of the Boltzmann-Langevin equation was carried out for a situation where the velocity field can be described by a set of N collective variables [28, 29]. In our previous study, the deduced Langevin equation was applied to investigate the isoscalar giant monopole resonance. In the present study, the framework is extended to investigate the isoscalar giant dipole resonance (IVGDR). The collective variable X for the IVGDR is set as the distance between the centers of the neutrons and the protons. The potential energy is found to be a function of the collective variable X is the harmonic-oscillator-type. By the self-consistent solution of the Langevin equation without damping and with random force, the calculations of the IVGDR energies for spherical nuclei reproduce the general trend of the data in spherical nuclei. Using the set of 37 Skyrme functionals to perform the calculation, the IVGDR energies were found to be sensitive to the symmetry energy at subnormal density. The evolution of the isospin asymmetry in the IVGDR demonstrates that the symmetry energy at density 0.02 fm^?3 has the largest contribution to the potential well. By comparing the calculations with the data, the functionals MSk2 and SLy230a provide the symmetry energies of 8.13 MeV and 9.54 MeV at a density of 0.02 fm^?3, respectively.