现今精度最高的地震成像方法是诞生于上世纪70年代的地震全波形反演方法。与传统的射线方法不同,全波形反演方法是基于地震波波场的成像方法。它的终极目标是利用接收到的地震波全部信息来推断地球的结构特征和动力学信息,例如获得油气藏储层参数、定位地下热点以及监测地震活动和板块活动中的应力场变化等。在过去10年间,得益于计算能力的提高和数值算法的进步,全波形反演方法在解决诸多实际问题中取得了成功。从小微尺度的超声波医学成像,到中等尺度的勘探地震成像再到全尺度的地球内部成像,全波形反演方法的应用场景跨越了足有9个量级的频率及波长。全波形反演方法成功预测了Valhall油田气层下部的新近世冰川印记,位于比利牛斯山脉西部的伊比利亚地壳推覆体,全球范围内俯冲带的俯冲结构以及非洲超级地幔柱的结构特征。展望未来,随着计算资源的提高及算法效率的提升,全波形反演方法将会呈现出更为精确的地球内部结构以及物理和化学模型参数。普林斯顿大学布莱尔讲席教授Jeroen Tromp在Nature Reviews Earth & Environment期刊发表综述文章,回顾了全波形反演方法的发展历史、基本方法及若干跨尺度的应用实例并展望了该方法的发展方向及挑战。
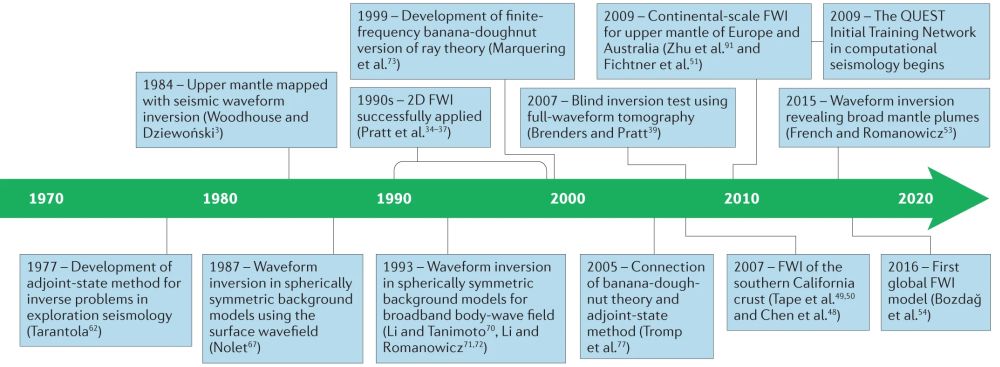
图1 地震全波形反演方法主要发展线(Tromp, 2019)
一、基本原理及关键因素
全波形反演方法的基本原理是通过不断比较模拟地震波形数据与观测地震数据来迭代更新地球参数模型(一般为纵、横波速度和密度)。当预测数据与观测数据足够接近时,我们认为此时的地球参数模型也就足以近似地球内部的真实情况。为了生成预测数据,我们需要考虑震源、初始模型及所用的正演模拟方法;为了比较预测数据和观测数据的不同,我们需要选取合适的目标函数;最终数据域的残差通过数据反传映射到模型域并通过优化算法更新参数模型。这些也是决定全波形反演方法应用效果的关键因素。
1.震源
一般而言,数值模拟所用的震源需要接近观测数据的真实震源以确保数据残差是由于模型参数的不精确引起的。在求解区域及全球尺度问题时,所用的震源一般为天然地震事件,相应的震源信息需要在反演之初求解(如CMT解)并在迭代过程中适时更新(震源和模型联合反演)。勘探应用一般选取主动源数据,震源信息较易获得。当震源信息缺失或者不够精确时,也可考虑之前提到的震源与模型联合反演。由于震源反演与模型反演存在一定程度的串扰,现在也发展出了一些不依赖于震源的反演方法(如双差反演)来避免反演震源信息。
2.初始模型
对于经典全波形反演算法而言,初始模型需要足够接近真实模型以避免反演陷入局部极值。即基于初始模型得到的预测数据与观测数据的波形(走时)差异要控制在半个波长范围内。区域及全球尺度的应用往往有较为精确的一维甚至三维参考模型,这些模型对常用的长周期观测数据来说已经是足够精确的初始模型了。相反的,勘探应用中并没有足够精确的初始模型。因此,对勘探地震来说,建立初始模型是首要任务。一些针对全波形反演的长炮检距、低频(~1.5 Hz)数据采集工作已经在一些石油公司展开;同时一些可以突破半波长准则限制的目标函数也被陆续提出。
3.正演模拟
对于给定的震源和初始模型,若要得到预测地震数据,我们需要模拟地震波的传播过程即正演模拟。在这里我们考虑两个问题:选用的波动方程和求解该方程的数值算法。在很长的一段时间内,石油工业界主要采用时间域有限差分方法求解声波波动方程。这主要是基于计算效率、算法复杂度及观测数据的特点考量的。随着勘探目标的转移,应用于陆地资料处理的弹性波波动方程也逐渐得以应用。与工业界不同,地震学家偏好(黏)弹性方程来处理观测到的横波及面波数据。时间域的谱元法因其在处理起伏地表、流固耦合界面及核幔边界(CMB)的高精度优势也得到了地震学家的青睐。
4.目标函数
作为衡量模拟数据与观测数据近似程度的指标和模型更新方向的指示(伴随震源),目标函数在某种程度上决定了反演的成败。经典的全波形反演方法选用模拟数据与观测数据的最小二乘差异作为目标函数,该目标函数只有在模拟数据与观测数据较为接近(半波长准则)时才有唯一局部极小值,因此在应用局部优化算法时对初始模型和数据频率范围有较高要求。一般来说,我们需要根据需要匹配的数据特点来合理选取目标函数。例如,当观测数据有明显的离群点时,L1范数要优于L2范数(最小二乘)。在解决区域及全球的反演问题时,地震学家往往选取那些与观测数据较为接近的模拟数据参与反演并且优先匹配地震数据中的相位(走时)信息。这是由于地震波振幅信息受震源的不确定性、记录仪器的影响往往难以匹配。由于初始模型较为精确,全波形反演问题中常见的周波跳跃(非唯一局部极值)问题在区域及全球反演问题中并不突出。但该问题却是自全波形反演方法诞生以来一直困扰勘探地球物理学家的棘手问题。相应地,勘探地球物理学家可以在反演之初选择较为简单的、与观测数据接近的模拟数据参与反演,如部分初至数据并逐渐增加数据选择范围。同时,勘探地震学家致力于寻找新的目标函数来突破半波长准则的限制。如自适应波形反演方法、震源-检波点拓展方法、时差拓展方法及最优输运方法等。严格意义上讲,现有的全波形反演算法并未使用全部的波形信息,而是使用尽量多的信息来约束反演模型。
5.数据反传
模型梯度为更新当前参数模型提供了更新方向。全波形反演方法可以使用弗雷谢特微分或者伴随状态法两种方法求取模型梯度。在当前数以亿计(大型三维模型)的模型参数条件下,计算每一模型参数的弗雷谢特微分并不可行。正是由于伴随状态法的提出,使得全波形反演算法实用化。藉此,模型梯度可以由正传波场与反传波场的互相关得到。所谓反传波场即由目标函数计算得到的伴随震源在检波点处沿时间反传得到。反传所用的方程为正传方程的伴随形式,所用的数值算法为之前提到的时间域有限差分或者谱元方法。在实际应用中,由于正传与反传波场存在传播时间上的差异,一般需要对正传波场做存储(硬盘)或者重建处理。
6.优化算法
现有的全波形反演方法使用基于梯度的局部优化算法,比如最速下降法、共轭梯度法、牛顿法、高斯-牛顿法以及拟牛顿法。其中L-BFGS方法被认为是最为实用的拟牛顿方法。然而这些局部优化方法都面临着同样的问题:收敛到局部极值。当该反演问题有唯一局部极值时,该局部极值即为全局最优解,反之反演结果将会是其中某一个局部最优解。反演问题局部极值的多少与上文谈到的初始模型、数据频带范围、正演算子与实际物理过程的近似程度及所用的目标函数等因素直接相关。
全波形反演方法与传统的基于射线理论的层析成像方法有着本质的区别。射线方法假设地球是简单的球形对称结构或者是近似的层状结构,地震波速度的异常是基于一阶扰动理论给出的。而全波形反演方法则可以适用于复杂的非均质模型,并考虑到了由此带来的高阶扰动。
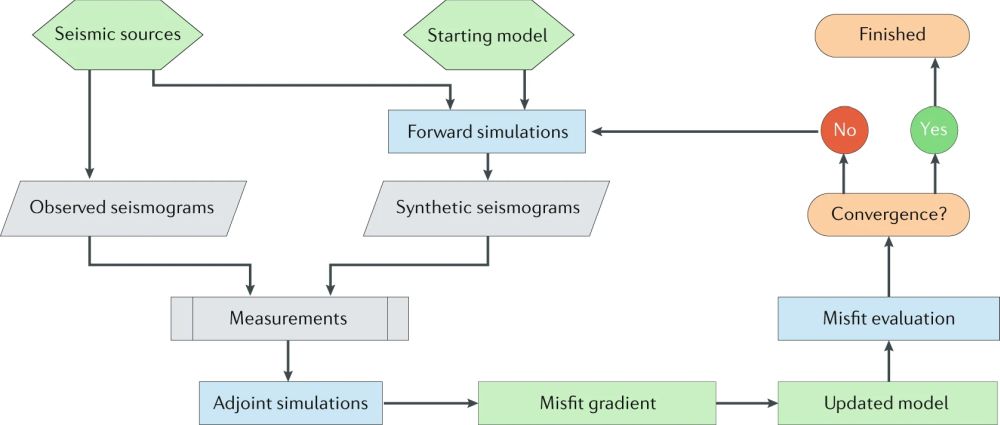
图2 全波形反演方法的基本流程(Tromp, 2019)
二、应用实例
地震全波形反演方法已经用于解决多种尺度的结构成像问题,如医学超声成像、无损探伤、地球近地表成像、勘探地球物理和区域及全球成像。所用的震源主要有主动源、天然地震以及环境噪声等。在这些应用中,全波形反演的基本方法并没有显著的不同,但是根据所接收的数据特点及反演目标的不同,上文所述的六大要素需要进行相应的调整。
1.勘探地震应用实例
过去十几年间,全波形反演方法在勘探地震学领域产生了深远影响。2007年盲测数据的成功应用给了勘探地球物理学家信心,自那时起对全波形反演方法的研究一直是勘探地球物理界的热点领域。值得一提的是全波形反演方法在北海地区Valhall油田的成功应用。该油田位于北海70 m深水区,由于浅部气层的存在,常规的射线方法难以对气层以下区域进行成像。石油公司在该地区采集了宽频带、宽方位角的海底电缆数据并应用多参数三维粘滞声波全波形反演。反演所用的频率范围为3.5-10 Hz,模型参数为各向异性纵波速度、密度及品质因子(Q)。如下图所示,全波形反演方法精确刻画出了浅层气藏、古河道沉积以及古海底的冰川移动划痕。
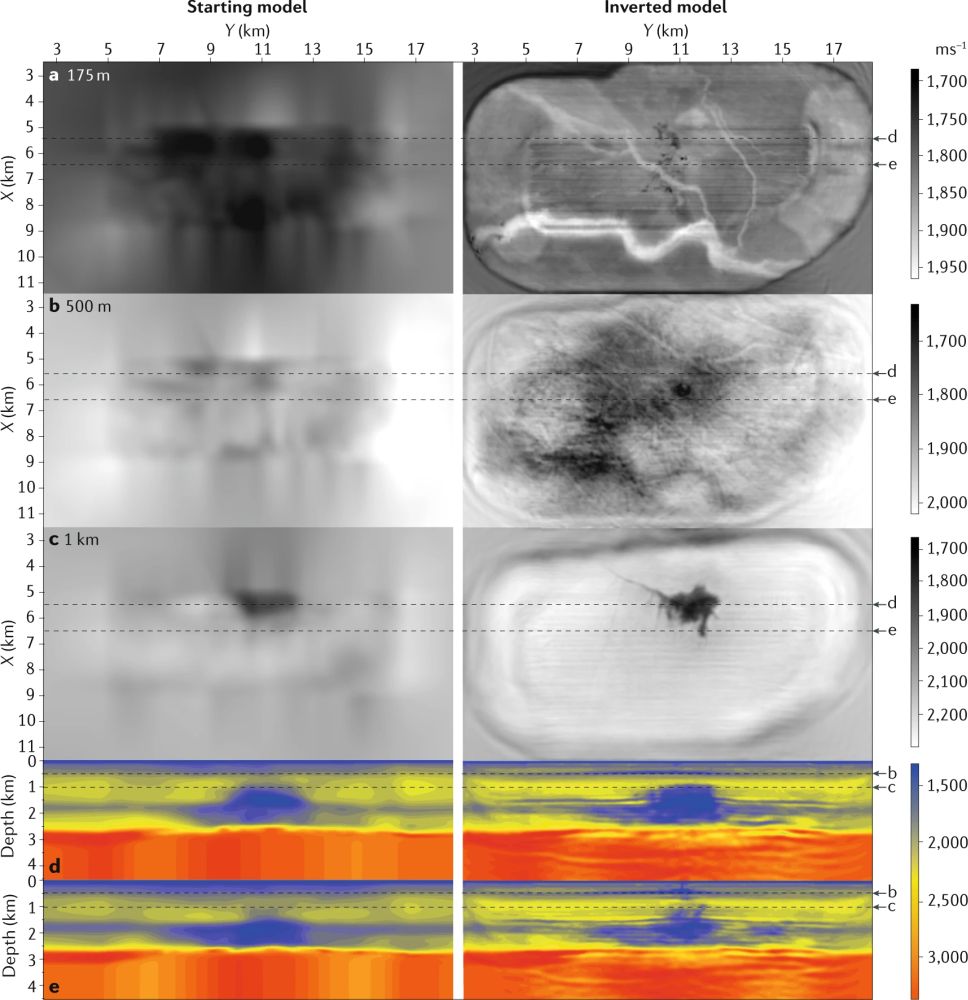
图3 Valhall油田的多参数粘滞声波全波形反演实例。左侧为初始垂向纵波速度模型(由反射走时层析成像获得);右侧为相应的更新模型。a-c为不同深度处的横向速度切片;在反演结果的175m深度(a)切片处可见古河道沉积及生产平台产生的散射点(X=6 km,Y=11 km);在500 m深度(b)切片处可见冰川移动在古海底留下的划痕;在1 km深度(c)切片处可见清晰的气藏结构以及裂缝构造。相应的构造特征在两处纵向速度剖面(d、e)中也有体现(Operto et al.,2018)
2.全球反演实例
首例全球尺度的全波形反演模型为GLAD-M15各向异性地幔模型。在2019年该模型被最新的GLAD-M25模型代替。该反演过程选取了1480个地震事件,在GLAD-M15模型的基础上增加了10次拟牛顿迭代更新。GLAD-M25模型刻画出了更为精细的地球内部结构:俯冲带地区的细节更加丰富、地幔柱的横波速度异常更加明显。
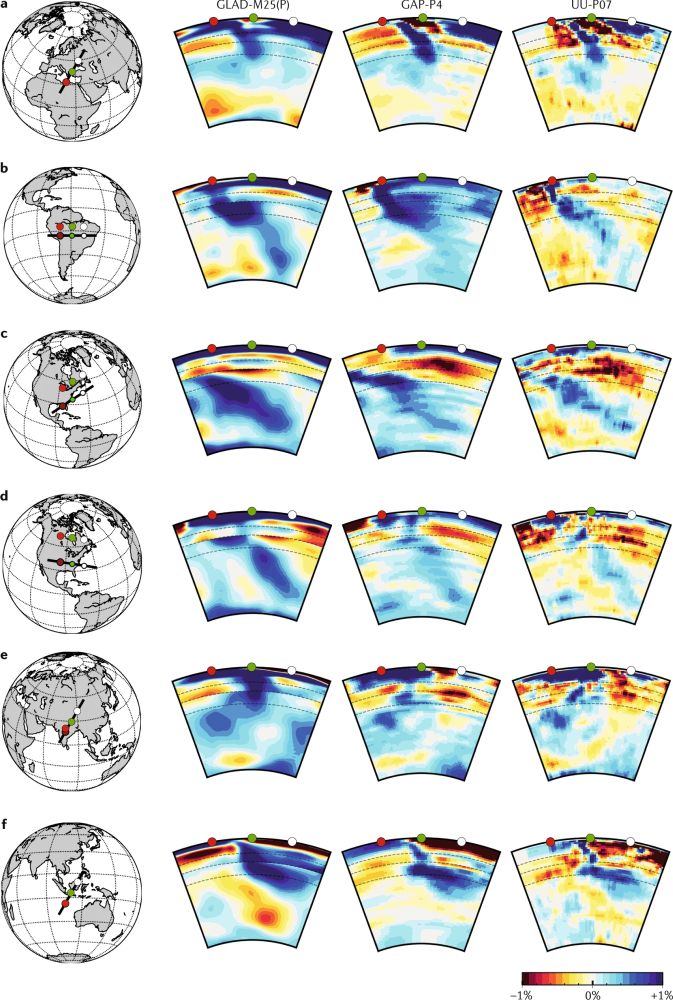
图4 哈特拉斯(Hatteras)俯冲带纵波速度扰动模型切片。红绿白圆圈标记了GLAD-M25模型及两个参考模型(GAP-P4及UU-P07)速度切片的位置(Lei et al.,2020)
三、机遇与挑战
在过去的四十多年间,尽管全波形反演方法取得了长足的发展,但其面临的最大挑战仍来自实际应用。一些实际应用中的棘手问题仍然存在,例如勘探问题中面临的初始速度模型问题、低频数据缺失问题以及全球反演中观测数据分布不均等问题。作者总结了全波形反演方法在地球科学应用中面临的机遇和挑战。
1.多参数反演
早期的全波形反演应用侧重于反演单一的速度模型。然而地震波在地下的传播过程还受到除速度以外的其他模型参数的影响,常见的有密度、传播方向(各向异性)以及吸收衰减(Q)等。考虑多参数的全波形反演方法在模拟地震波传播时更加接近真实的物理过程,这也就降低了由于传播算子不精确引起的反演不确定性。在勘探地球物理界,声波各向异性全波形反演已经得以应用,(黏)弹性全波形反演仍在探索中。对地震波的声波近似并不适用于全球反演问题,因此在区域及全球反演问题发展之初就将(黏)弹性全波形反演作为主要发展方向,并逐渐将各向异性参数纳入反演目标。多参数反演加剧了反演问题的病态程度。在有限的观测范围内(地表接收),模型参数间的串扰一直存在(如反射地震中的速度和密度),部分模型参数约束不足(如透射波对密度变化不敏感)。
2.计算效率
有限的计算资源仍然是制约全波形反演应用的主要因素。计算效率的提升主要考虑计算机硬件系统的进步和算法的优化两个方面。地球物理学家主要通过优化全波形反演算法及流程以提升计算效率,如平衡数值计算与输入/输出(I/O)负担、图形卡计算等。此外,反演结果的可视化对于解释反演结果、科学发现有重要作用。
3.反演结果的不确定性
受制于有限的观测系统和地震波的传播规律,反演模型的不同区域(如浅层和深层)、不同参数(如纵波速度和密度)的精确程度是不一样的。对反演结果的不确定性分析将会帮助解释反演结果、排除反演假象。目前对反演结果的不确定性分析仍处于探索阶段。常用的数值分析方法是对棋盘模型的算例分析,但是该方法相当于进行一次全波形反演,耗费大量计算资源。基于贝叶斯理论的不确定性分析方法有望在未来得以发展并应用。
4.震源编码
震源编码方法可以极大地降低全波形反演方法的计算量,但是也容易引入不同震源波场和观测数据波场之间的串扰问题。最新研究表明当地震波传播至稳态状态时,震源波场和反传波场可以准确解码,互相关得到的梯度更加准确。
5.全局搜索
如前文所述,现有的全波形反演方法依赖于基于梯度的局部优化算法。这也就不可避免地使反演过程收敛于某一个局部极值。基于贝叶斯理论的全局搜索算法有望跳出局部极值,找到全局最优解。然而这类方法的最大问题是需要对每一模型参数进行采样(如正演模拟),计算量巨大。汉密尔顿马科夫链蒙特卡洛方法因其可用伴随状态法求解有望降低计算量,使得全局搜索变得可行。
四、结论及展望
全波形反演方法经过四十多年的发展已经在科学界和工业界产生了巨大的影响。尽管该方法的成功应用仍然面临挑战,但它带来的回报吸引了来自科学界和工业界的持续投入和研究。对地震学家而言,全波形反演提高了地球内部成像精度、提高了人类对地球内部物理和化学过程的认识。对工业界而言,全波形反演帮助开发现有油藏、发现新的油藏,为石油公司带来丰厚的收入。展望未来,无串扰的震源编码方法、基于汉密尔顿蒙特卡洛方法的贝叶斯反演框架、机器学习及数据分析方法将会对全波形方法产生深远影响,进一步帮助人类认识地球内部结构。
原文:Tromp J. Seismic wavefield imaging of Earth’s interior across scales[J]. Nature Reviews Earth & Environment, 2019: 1-14.(链接)
(编译:张振东,刘伊克/油气室)
