显格式有限差分被广泛应用于地震波场数值模拟领域。然而，该方法的最大时间步长△t_max严格受到Courant-Friedrichs-Lewy (CFL)稳定性条件限制。当时间步长超过△t_max时，波场迭代不再稳定；此外，当时间步长接近△t_max时，数值频散噪音逐渐加重，因此，在地球物理数值模拟领域一直采用远小于△t_max的步长以获得更高的模拟精度。但是更小时间步长同时也意味着迭代次数将大幅度增加，计算量在长时程模拟时难以承受。采用大于△t_max所引发的不稳定现象本质上源于在原本为零的高波数区域出现了非零波场，这些波场的能量迅速放大直到发生肉眼可见的不稳定现象。
　　中科院地质与地球物理所地球与行星物理院重点实验室高英杰博士后与张金海研究员、合作导师姚振兴院士通过空间滤波的方法压制了这些高波数波场，使得可以采用比△t_max大得多的时间步长进行稳定的数值模拟。此外，他们还采用逆时离散变换方法有效修正大步长迭代所固有的数值频散噪音，从而实现了稳定而且准确的超长时间步长（即>△t_max）数值模拟，大幅度提升了计算效率。该研究是地震学领域继特征值扰动法（高英杰等- Geophysics：突破显式有限差分的稳定性条件限制）之后突破稳定性条件限制的新尝试，有望在全球尺度的多轮回波场传播、地震干涉数值模拟以及深层油气地震成像等领域获得应用。
　　当时间步长超过CFL稳定性条件的限制时，根据CFL稳定性条件曲线（图1），我们可以得到相应的角频率。不稳定噪声就产生在大于的波数区域，而波数值小于的有效波场分量仍然可以进行稳定迭代。随着时间步长的不断加大，逐渐减小。单次时间步长的波场迭代完成之后，通过采用低通滤波的思路，将大于的不稳定波场噪声滤除，就可以保证波场模拟的稳定迭代（图2）。
　　进一步采用逆时间频散变换法来去除由于大步长模拟造成的时间数值频散（图3a），获得了精确的模拟结果（图3b）。该方法所能采用的最大时间步长是CFL稳定性条件的数倍，在提高计算效率的同时，保证了数值模拟的精度。

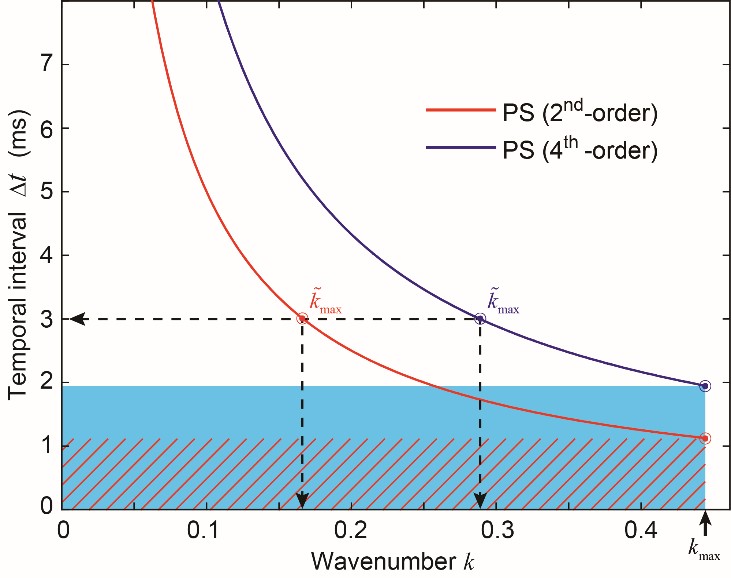
图1 二阶时间有限差分(PS (2^nd-order))和四阶时间有限差分(PS (4^th-order)) CFL稳定性条件所对应的曲线，其中是低通滤波器对应的角频率

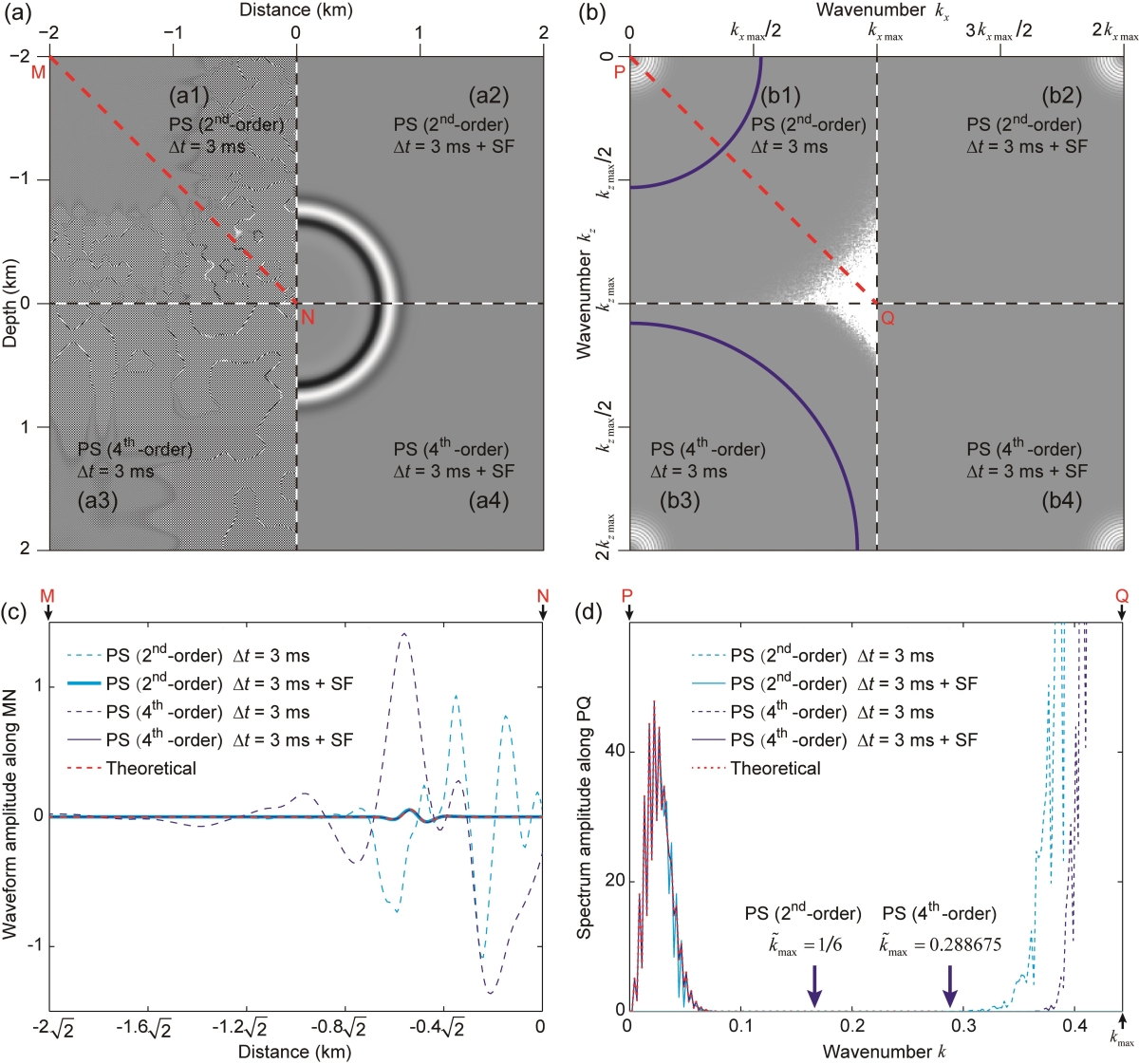
图2 基于二阶时间有限差分和四阶时间有限差分，采用时间步长Δt = 3 ms进行模拟所得的波场快照和相应的波数域频谱。(a1)和(a3)是从300 ms起停止空间滤波，经过数次迭代所得到的333ms波场快照。(a2)和(a4)是分别对(a1)和(a3)采用空间滤波之后得到的快照。(b1)-(b4)是(a1)-(a4)相应波数域频谱，(b1)和(b3)中的蓝色圆弧分别是二阶时间有限差分和四阶时间有限差分对应低通滤波器的角频率。(c)和(d)分别是(a)和(b)中沿红色虚线的波形剖面。本实验中，二阶时间有限差分和四阶时间有限差分CFL稳定性条件所允许的最大时间步长分别为1.125 ms和1.949 ms

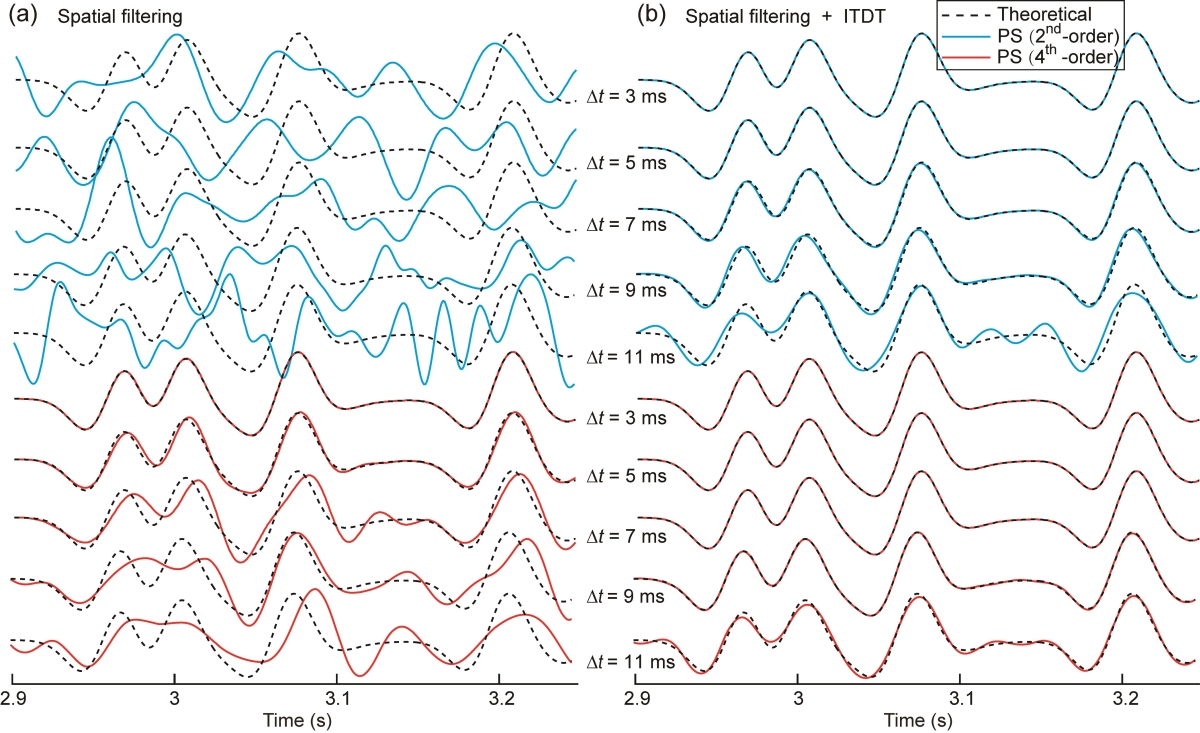
图3 利用不同时间步长获得的单道波形记录。基于二阶时间有限差分和四阶时间有限差分依次测试了时间步长Δt = 3, 5, 7, 9, 11 ms。(a)是采用过空间滤波算法之后得到的模拟波形；(b)是对(a)采用了逆时离散时间变换后的结果。本实验中，二阶时间有限差分和四阶时间有限差分CFL稳定性条件所允许的最大时间步长分别为1.125 ms 和1.949 ms　　
　　研究成果发表于Journal of Computational Physics。(Gao Y J, Zhang J H^*, Yao Z X. Extending the stability limit of explicit scheme with spatial filtering for solving wave equations[J]. Journal of Computational Physics, 2019, 397: 108853. DOI: 10.1016/j.jcp.2019.07.051)(原文链接)