
 , 王颖
, 王颖 中国科学院大学人工智能学院, 北京 100049
2019年1月29日 收稿; 2019年3月18日 收修改稿
基金项目: 国家自然科学基金(61471338)、中国科学院青年促进会(2015361)、中国科学院前沿科学重点研究项目(QYZDY-SSW-SYS004)、北京市科技新星计划(Z171100001117048)和北京市科技计划课题(Z181100003818019)资助
通信作者: 肖俊,E-mail:xiaojun@ucas.ac.cn
摘要: 岩体点云滤波是岩体三维重建的关键环节。针对岩体点云环境,提出一种基于多维度特征和多层神经网络的植被滤波方法。该方法首先计算点云中每一点的多维度特征作为特征输入;然后利用多层神经网络构建分类器实现对岩体点云数据的植被滤波过程。分析多维度特征的可用性,并通过不同的实验过程筛选最优网络模型参数。与其他分类器相比,本算法精度较高,能够更好地应用于岩体点云植被滤波领域。
关键词: 岩体点云植被滤波维度特征多层神经网络(MLP)
A vegetation filtering method for rock mass point clouds based on multi-dimensionality features and MLP
HU Liang, XIAO Jun

 , WANG Ying
, WANG Ying School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing 100049, China
Abstract: Filtering on rock mass point clouds is an important step in 3D rock mass reconstruction. This work focuses on rock mass point clouds and we propose a vegetation filtering method based on multi-dimensionality features and MLP(multi-layer perceptron). This method firstly calculates multi-dimensionality features for each point. Then, MLP is used for training the classifier, which can be applied in vegetation filtering. We analyze the availability of multi-dimensionality features and select the best MLP model through different experimental processes. The experimental results show that the proposed method has a higher precision than other classifiers and it can be better applied in the field of rock mass point cloud vegetation filtering.
Keywords: rock mass point cloudsvegetation filteringdimensionality featuresmulti-layer perceptron
激光扫描技术[1]可以快速直接地获取目标物体高精度、高密度的三维空间信息,被广泛应用于三维模型重建、三维目标识别和虚拟现实等领域。在岩石工程领域,需要利用有限元、离散元、不连续变形分析[2]等数值计算方法对岩体三维数据模型进行数值分析,以保证工程实施的安全性[3]。激光扫描技术可以提供高精度的岩体表面三维空间信息,这些三维点云数据可以作为基本的数据输入有效地构建岩体三维数值模型。但是,通过激光扫描仪获取的初始岩体点云表面往往含有一些植被点,这些植被点会严重影响后续的建模过程,需要被过滤。由于岩体本身的特殊性例如表面不规则、朝向不统一、粗糙程度不一和尺度变化较大的特点[4],传统的点云植被滤波方法在岩体点云上难以取得较好的结果。因此针对岩体点云的植被滤波是一个亟需解决的问题。
经典的点云植被滤波算法,主要分为基于形态学的滤波[5]、基于坡度的滤波[6]、基于渐进三角网格的滤波[7]和基于窗口拟合的滤波[8]。这些滤波方法主要针对大场景的机载雷达点云数据,滤除植被信息以获得数字高层模型。这类算法主要利用植被与地面高程差的变化进行滤波。然而,大多数岩体自身高程变化较大,且植被多附着于岩体表面生长,与岩体的高程差不明显,因此难以利用典型滤波算法在岩体点云上获得较好的滤波结果。Liu等[9]将典型滤波算法在岩体点云数据上进行比较,其实验结果验证经典植被滤波算法在岩体点云上性能较低。此外,部分激光扫描仪可以获取多次回波数据,Pirotti等[10]利用首次回波和尾次回波参与滤波运算,滤除掉首次回波的点云,然后再根据反射比和形态学的方法得到最终结果。但是这种方法对设备依赖很高且对植被与地面边界处的点云难以进行有效的区分。
目前岩体点云滤波的难点是由岩体点云本身特征所决定的,由于岩体点云中的岩体点和植被点的高程值并不具有显著的差异性,因此难以用传统的点云植被滤波思路解决岩体点云的植被滤波问题,但是如果将植被滤波过程看作是岩体点与植被点的二分类问题,则可以利用深度学习或者机器学习的方法实现岩体点云的植被滤波过程。
在机器学习领域进行数据分类的通用做法是首先对数据进行分析,提取出具有代表性的特性,然后利用人工神经网络、支持向量机(support vector machine, SVM)以及朴素贝叶斯等分类器快速实现对数据的分类,其难点是如何提取合适、通用的特征。通过激光扫描仪获取的点云数据一般包括三维坐标信息、颜色信息以及强度信息。但是岩体点云中的三维坐标是无序且无规则的,难以直接用作分类特征选择;苍桂华等[11]分析强度信息会受仪器设备、外界环境条件、地物表面特性和地物扫描几何条件等因素的影响,因此不能直接用于分类;颜色信息会受到强阴影投影,图像曝光变化以及表面湿度的影响也难以作为分类特征的选择[12]。Brodu和Lague[13]在三维点云数据中分析不同地物点特征,发现其局部维度特征具有差异性,然后利用三维局部维度特征实现河床点云分类并取得较好的结果。
在深度学习领域,可以通过搭建深度神经网络自动提取学习特征,解决了传统机器学习需要提取特征的难题。但是,目前深度学习算法仅被广泛应用于二维图像领域,在三维点云数据上的分类与识别尚处于研究阶段[14]。Qi等[15-16]提出PointNet++网络可以实现对点云数据的分类。但是深度网络往往需要大量数据的支持,且三维点云数据不同于二维图像数据,其维度较高,信息量更大,通常训练难度更大。
基于以上分析,考虑到岩体点云数据缺少标准数据库的支持且训练复杂度较高,本文针对工程岩体点云的植被滤波问题,提出一种基于多维度特征和多层神经网络(multi-layer perceptron, MLP)的岩体点云植被滤波方法。首先定义点云中的多尺度局部维度特征,并分析其应用于岩体点云植被分类的可用性。其次,由于多尺度维度特征通常是非线性特征,本文选择非线性能力较强的MLP作为分类器并通过实验选择分类器参数。目前神经网络架构较为成熟,其难点主要是针对特定特征的参数选择,例如特征数目、网络深度、网络层结点个数、过拟合参数、学习率等,以训练出最优的效果。最后通过设置好的参数,训练出最终模型,相比其他机器学习算法,本文算法在测试集上具有更高的分类精度,可用于岩体点云的植被滤波过程。其滤波结果可以提高后续的岩体三维建模精度,在岩体工程领域具有较大的应用价值。
1 特征提取本文利用点云数据的多尺度维度特征作为分类依据。维度特征的定义方式如图 1(a)所示,以点云中任意一点为中心点建立半径尺度为R的邻域球,该点与其邻域内的其他点组成的局部空间内可以形成3种不同的维度特征,如图 1(b)所示,分别为一维线性特征、二维平面特征和三维立体特征。
Fig. 1
 | Download: JPG larger image |
| 图 1 不同维度特征 Fig. 1 Different dimensionality features 图 1 不同维度特征 Fig. 1 Different dimensionality features --> | |
不同的分类物体在不同尺度下的维度差异越明显,则说明可分性越强。如图 2所示,自然界的岩体表面往往是由大尺度的平面构成,因此其在不同尺度下近似表现为二维平面特征[17],而植被点云在小尺度下可能表现为一维特征(树干)或者二维特征(树叶),在较大的尺度下,展现出三维特征。因此,在工程点云中,岩体点与植被点在多尺度的综合特征下具有显著的维度差异,该特征可被用于进行岩体点云上的植被点与岩石点的分类。
Fig. 2
 | Download: JPG larger image |
| 图 2 不同分类物的维度特征 Fig. 2 Dimensionality features of different objects 图 2 不同分类物的维度特征 Fig. 2 Dimensionality features of different objects --> | |
2 算法流程以及模型构建2.1 岩体点云植被滤波算法流程本文主要聚焦于岩体点云中植被滤波问题。在分析不同尺度下分类物体维度特征的基础上,构建多层神经网络模型以实现点云的精确分类。该算法的具体流程如下:
1) 对获取的初始岩体点云,首先需要滤除噪声,其中主要是对离群点的过滤,然后计算点云的平均间隔;
2) 对过滤后的点云,手动选取部分具有代表性的子集,并对点云内岩体点和植被点进行标签分类;然后将该点云随机划分为训练集和测试集;
3) 设置不同的尺度范围以及尺度间隔,最小尺度一般大于点云的平均间隔;在不同尺度下,计算每个点的维度特征,作为分类依据;
4) 建立不同的神经网络模型,在测试集上选取精度最高的模型作为最佳分类器;
5) 将分类器应用于整个点云以实现对整个大规模岩体点云的植被滤波。
2.2 点云预处理在预处理阶段主要是对点云数据的去噪以及点云的分类工作。通过激光扫描仪获取的初始点云,受采集环境以及设备影响会含有部分噪声,其中主要以离群点集(孤立点群)为主。离群点其周围含有极少量的点,邻域特征不随尺度变化,会对后续分类训练结果产生较大影响,因此需要进行滤除。目前常用的离群点集判断方法,是利用空间邻域搜索的方法快速将点云分割成若干子区域,然后删除含有点数较少的子区域。
对过滤后的点云,手动选取部分具有代表性的子集,并对点云内岩体点和植被点进行标签分类。然后将点云随机划分为训练集和测试集。训练集用于模型训练,测试集用于估计模型的泛化误差以选择最优的分类器。
2.3 多尺度维度特征提取目前最广泛的局部维度特征的计算方法是利用主成分分析法(principal component analysis,PCA)。对于点云集合P中的任意一点pi=(xi, yi, zi)在半径为R的尺度内,共包含n个点,利用式(1)构建协方差矩阵Σ,并利用式(2)计算该矩阵的特征值,其中q=(x, y, z)代表整个区域内的中心值,λ1≥λ2≥λ3代表协方差矩阵的3个特征值,vj代表特征值对应的特征向量。
| $\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {{\mathit{\boldsymbol{p}}_i} - \mathit{\boldsymbol{q}}} \right)} {\left( {{\mathit{\boldsymbol{p}}_i} - \mathit{\boldsymbol{q}}} \right)^{\rm{T}}}, $ | (1) |
| $\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \cdot {\mathit{\boldsymbol{v}}_j} = {\lambda _j} \cdot {\mathit{\boldsymbol{v}}_j}, j \in \{ 0, 1, 2\} .$ | (2) |
| ${q_i} = \frac{{{\lambda _i}}}{{{\lambda _1} + {\lambda _2} + {\lambda _3}}}, i \in \{ 1, 2, 3\} .$ | (3) |
| ${\rm{ Loss }} = - (z\log y + (1 - z)\log (1 - y)).$ | (4) |
| $y_j^{(l)} = f\left( {\sum\limits_{i \in (l - 1)} {w_j^{(l)}} x_i^{(l - 1)} + b_j^{(l)}} \right).$ | (5) |
Table 1
| 表 1 MLP模型基本参数Table 1 Parameters used in MLP |
3.1 实验数据分析本实验所用的岩体点云数据来源于岩体通用的数据库Rockbench[4],其利用激光扫描仪获取加拿大安大略的一处包含植被的岩体点云数据。如图 3所示,该点云是从原始大场景的岩体点云中截取的部分具有代表性的点云数据并人工分类后的示意图,其中深色表示植被点,浅色部分表示岩体点,该实验的数据集包括高的树木以及低矮的植被信息。为了后续的训练过程,需要将初始的点云数据按照7:3的比例划分为训练集与测试集,具体各个数据集的信息如表 2所示。
Fig. 3
 | Download: JPG larger image |
| 图 3 实验岩体点云数据 Fig. 3 Rock mass data for the experiments 图 3 实验岩体点云数据 Fig. 3 Rock mass data for the experiments --> | |
Table 2
| 表 2 实验数据集信息Table 2 Information of data set for the experiments |
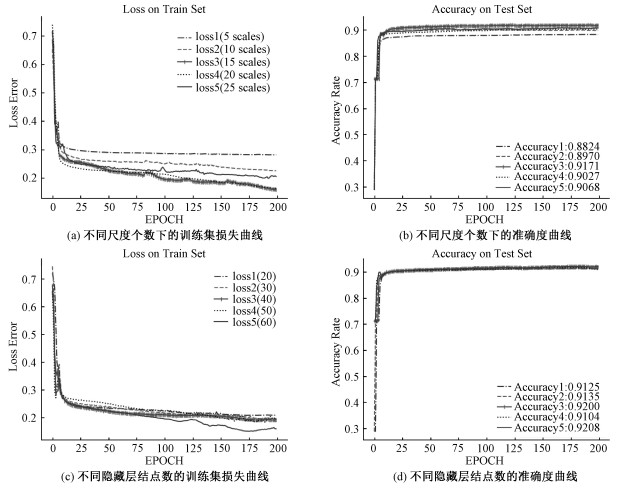
3.2 不同的尺度选择对结果的影响本实验通过在训练集上分别选取5组{5, 10, 15, 20, 30}不同尺度个数作为特征输入构建不同的网络模型,通过损失函数和测试集的精确度筛选出最佳尺度个数,尺度范围从0.2开始,尺度间隔选取为0.1,其他参数选择表 1的初始参数。
5组不同的MLP模型在训练集上随着训练次数的损失函数结果如图 4(a)所示,可以看出,不同数量尺度的特征在该网络结构中均可以快速达到收敛,其中测试数据集在15个尺度下的网络模型达到最好的收敛效果。不同的网络模型在测试集上的准确度如图 4(b)所示,从结果可以看出15个尺度的网络模型精确度最高。综上,在该岩体数据集上选择的最佳尺度个数为15。
Fig. 4
 | Download: JPG larger image |
| 图 4 不同模型在不同尺度个数和不同隐藏结点个数下的训练集测试结果 Fig. 4 Results of different models on training sets and test sets with different scales and hidden sizes 图 4 不同模型在不同尺度个数和不同隐藏结点个数下的训练集测试结果 Fig. 4 Results of different models on training sets and test sets with different scales and hidden sizes --> | |
3.3 不同隐藏层结点数对结果的影响为了测试隐藏层不同的结点数目对实验结果的影响。本实验测试了隐藏层结点数分别为{20, 30, 40, 50, 60}的5组不同的网络模型。根据3.2节结果,该5组模型均选取15个尺度特征作为输入,其余参数使用表 1的默认参数,实验结果如图 4(c)、4(d)所示。可以看出当选取15个尺度特征作为输入的前提下,隐藏层节点个数对该数据集的训练结果影响不大,均可以快速收敛并在测试集上获得较好的训练结果(准确度大于90%)。综合3.2与3.3节的实验结果,本实验的模型最终选择15个不同的尺度特征作为特征输入同时选取60个隐藏层结点数以搭建适合此数据集的多层神经网络模型。
3.4 实验比较目前常用的机器学习分类器有很多,包括SVM、朴素贝叶斯、决策树和神经网络方法。由于在岩体点云中多尺度的维度特征在分类时展现出较多的非线性特性,因此MLP可以利用其多层网络结构实现较为精确的分类。
本实验选用SVM和朴素贝叶斯作为比较算法,SVM是目前常用的分类器,它可以实现线性和非线性分类;朴素贝叶斯是一种基于概率的分类器,它以贝叶斯理论为基础,对不同维度特征通过概率计算以实现分类过程。除此之外,Xiao等[18]提出一种利用人工神经网络进行植被分类的方法,取得了较好的结果,因此也被用于作为对比算法。
在本实验中统计了查准率、召回率以及F1值作为性能评测标准,相较于单纯测试准确度,F1值能够更好地反映模型对整个数据样本的分类能力。实验结果如表 3所示,可以看出针对岩体点云上多尺度维度特征的分类问题,本文提出的MLP算法相比SVM、朴素贝叶斯算法以及人工神经网络算法具有更好的分类精度。
Table 3
| 表 3 不同分类器实验结果比较Table 3 Performance comparison among four different methods |
实验的仿真结果如图 5所示,其中浅色为正确分类的点,深色为错误分类的点。可以看出,本文提出的滤波模型,可以滤除大部分的高处植被,只是在低矮植被处有部分错误,相比于图 3的初始点云数据,本文提出的算法可以较好滤除岩体点云中的植被信息。
Fig. 5
 | Download: JPG larger image |
| 图 5 网络模型在整个数据集实验结果 Fig. 5 Filtering results in data set using our models 图 5 网络模型在整个数据集实验结果 Fig. 5 Filtering results in data set using our models --> | |
此外,测试了该模型在未标注的新数据集上的结果,共包含192 303个点,此数据集与测试数据集来自同一岩体数据库,实验结果如图 6所示,其中深色代表分类为植被的点,浅色代表分类为岩体的点。可以看出,本文提出的算法,可以较好地应用于工程岩体点云的植被滤波过程。
Fig. 6
 | Download: JPG larger image |
| 图 6 网络模型在新数据集实验结果 Fig. 6 Filtering results in new data set using our models 图 6 网络模型在新数据集实验结果 Fig. 6 Filtering results in new data set using our models --> | |
4 总结本文针对工程岩体点云的植被滤波问题提出一种基于多维度特征和MLP的植被滤波算法。该算法可以实现将高大数木、稀疏植被以及低矮植被等常见的植被点从岩石点云中分离出来,并具有较高的精度。由于多尺度的维度特征是基于统计计算的方法,只利用了点云的三维坐标信息,因此具有较高的适用性,可以应用于各类激光扫描场景中。该算法通过实验选择最优尺度个数与网络模型参数,相对于SVM、朴素贝叶斯等分类算法具有较明显的优势。其滤波结果可以很好地应用于后续岩体三维重建过程。但是,该算法在处理密度严重不均匀的点云数据以及岩体边界处点云数据的适用性仍需加强。
参考文献
| [1] | Wilkes P, Lau A, Disney M, et al. Data acquisition considerations for terrestrial laser scanning of forest plots[J]. Remote Sensing of Environment, 2017, 196: 140-153. Doi:10.1016/j.rse.2017.04.030 |
| [2] | Zhu H, Wu W, Chen J, et al. Integration of three dimensional discontinuous deformation analysis (DDA) with binocular photogrammetry for stability analysis of tunnels in blocky rockmass[J]. Tunneling and Underground Space Technology, 2016, 51: 30-40. Doi:10.1016/j.tust.2015.10.012 |
| [3] | He L, An X M, Ma G W, et al. Development of three-dimensional numerical manifold method for jointed rock slope stability analysis[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 64(6): 22-35. |
| [4] | Lato M, Kemeny J, Harrap R M, et al. Rock bench:establishing a common repository and standards for assessing rockmass characteristics using LiDAR and photogrammetry[J]. Computers and Geosciences, 2013, 50(1): 106-114. |
| [5] | Zhang K, Chen S C, Whitman D, et al. A progressive morphological filter for removing nonground measurements from airborne LIDAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 872-882. Doi:10.1109/TGRS.2003.810682 |
| [6] | Vosselman G. Slope based filtering of laser altimetry data[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(3): 935-942. |
| [7] | Axelsson P. DEM generation from laser scanner data using adaptive TIN models[J]. International Archives of Photo-grammetry and Remote Sensing, 2000, 33(4): 110-117. |
| [8] | Liu C, Li J, Zhang S, et al. A point clouds filtering algorithm based on grid partition and moving least squares[J]. Procedia Engineering, 2012, 28: 476-482. Doi:10.1016/j.proeng.2012.01.754 |
| [9] | Liu S D, Hu L, Shi T X, et al. Comparison of filtering algorithms for rock point cloud data[C]//International Conference on Advanced Materials and Computer Science, 2016: 101-107. |
| [10] | Pirotti F, Guarnieri A, Vettore A. Ground filtering and vegetation mapping using multi-return terrestrial laser scanning[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 76: 56-63. Doi:10.1016/j.isprsjprs.2012.08.003 |
| [11] | 苍桂华, 岳建平, 潘邦龙. 地面激光扫描强度数据的影响因素分析[J]. 测绘科学技术学报, 2014(3): 257-262. Doi:10.3969/j.issn.1673-6338.2014.03.009 |
| [12] | Lague D, Brodu N, Leroux J. Accurate 3D comparison of complex topography with terrestrial laser scanner:application to the Rangitikei canyon (N-Z)[J]. ISPRS journal of photogrammetry and remote sensing, 2013, 82: 10-26. Doi:10.1016/j.isprsjprs.2013.04.009 |
| [13] | Brodu N, Lague D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion:applications in geomorphology[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 68: 121-134. Doi:10.1016/j.isprsjprs.2012.01.006 |
| [14] | Charles R Q, Su H, Matthias N, et al. Volumetric and multi-view cnns for object classification on 3d data[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 5648-5656. |
| [15] | Qi C R, Su H, Mo K, et al. Pointnet: deep learning on point sets for 3d classification and segmentation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 652-660. |
| [16] | Qi C R, Yi L, Su H, et al. Pointnet++: deep hierarchical feature learning on point sets in a metric space[C]//Advances in Neural Information Processing Systems, 2017: 5099-5108. |
| [17] | Umili G, Ferrero A, Einstein H H. A new method for automatic discontinuity traces sampling on rock mass 3D model[J]. Computers and Geosciences, 2013, 51: 182-192. Doi:10.1016/j.cageo.2012.07.026 |
| [18] | Xiao J, Liu S D, Hu L, et al. Filtering method of rock points based on BP neural network and principal component analysis[J]. Frontiers of Computer Science, 2018, 12(6): 1149-1159. Doi:10.1007/s11704-016-6170-6 |
