基于数码相机的玉米冠层SPAD遥感估算

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-26

贺英, 邓磊, 毛智慧, 孙杰. 基于数码相机的玉米冠层SPAD遥感估算[J]. 中国农业科学, 2018, 51(15): 2886-2897 https://doi.org/10.3864/j.issn.0578-1752.2018.15.005
HE Ying, DENG Lei, MAO ZhiHui, SUN Jie. Remote Sensing Estimation of Canopy SPAD Value for Maize Based on Digital Camera[J]. Scientia Acricultura Sinica, 2018, 51(15): 2886-2897 https://doi.org/10.3864/j.issn.0578-1752.2018.15.005

0 引言

【研究意义】叶绿素是植物光合作用中最重要的色素,其含量高低反映了作物光合能力的强弱和营养生理状况的好坏,是评价农作物长势的重要指标^[1,2]。【前人研究进展】MARENCO等^[3]研究发现使用SPAD-502 测量叶绿素含量的精度很高,几乎跟化学试验测得的叶绿素结果一样,因此可以用SPAD值代替叶绿素的含量。该方法虽然能够准确地、无损地获取作物叶片SPAD值,但SPAD叶绿素仪测定面积小,大面积测定需要大量时间^[4]。近年来对地观测技术快速发展,国内外****使用卫星影像在不同尺度测定作物光谱从而对作物叶绿素含量以及叶绿素相对含量进行反演和估算^[5,6],该方法具有覆盖面积广的优势,但卫星数据存在重访周期长、易受云、雨影响等缺点,限制了其在农业遥感中实时、连续监测的应用^[7]。随着数码图像采集设备和计算机图像处理技术的发展,无人机以其机动灵活、操作简便、按需获取数据且空间分辨率高的优势,通过搭载高光谱、多光谱相机成为获取作物叶绿素相对含量的重要手段^[8,9]。HUNT^[10]、SCHLEMMER^[11]、房贤一^[12]和张潇元等^[13]利用各种植被指数构建了估测作物叶片叶绿素含量和叶氮含量的遥感模型。丁希斌等^[2]利用高光谱成像技术,分别通过全谱、特征波长、红边参数和植被指数4种方式,将光谱信息与SPAD值联系起来,建立油菜叶片的SPAD预测模型。以上的方法都能实现SPAD值的估测,但所使用的大多数指数都包含可见光及近红外波段,然而在国内外无人机的实际应用中,考虑到传感器获取的难易、后期数据处理的复杂度及成本等原因,对仅包含可见光波段的无人机影像获取更为容易,应用也更为广泛。自然界中物体的颜色是由其在波长400—700 nm的可见光光谱反射特性决定的,而正常生长的作物叶片颜色由叶绿素的光谱特性决定,因此,可见光区域的反射光谱的特性可以用来估测叶片的叶绿素含量^[14,15]。JIA等^[16]指出绿光亮度值与小麦冠层氮素浓度和叶片SPAD值有显著的负相关关系。PAGOLA等^[17]利用图像分析技术提取大麦叶片的色彩指数发现,其与叶绿素含量有显著的相关性。王方永等^[18]提出可见光通道的G-R参数能够较好的预测棉花叶绿素含量。在构建SPAD估测模型的过程中,有****将计算机领域的机器学习算法应用于作物SPAD值的遥感估算研究中^[19,20]。其中,KARIMI等^[21]以玉米为研究对象,利用支持向量回归算法,将从高光谱数据提取的指数与实测SAPD进行拟合;LIU等^[22]利用BP神经网络模型建立水稻SPAD值与光谱参数的关系;KIRA等^[23]基于高光谱波段计算植被指数,利用最小二乘法和神经网络算法建立模型估算了3种树木的叶绿素;王丽爱等^[24]使用随机森林回归算法构建小麦叶片SPAD值的遥感估算模型。【本研究切入点】近年来,数码影像由于其成本低、获取简单、性价比高等优势逐渐成为低空遥感的重要手段,机器学习中各种算法也被广泛应用于农作物生理生化参数的估测,但利用随机森林回归算法构建仅包含可见光波段的冠层叶绿素相对含量的研究尚不多见。【拟解决的关键问题】本研究以玉米为目标作物,综合分析开花期玉米冠层可见光植被指数与冠层SPAD值的相关关系,采用单变量回归模型、多元逐步回归模型和随机森林回归算法构建玉米冠层SPAD值的遥感估算模型。以期为数码相机在农作物SPAD估算中的应用提供新的研究手段和新的经验。

1 材料与方法

1.1 研究区概况

试验区地处河北省涿州市城西十公里处东城坊镇（东经115°50′56″,北纬39°27′49″）。该地区属暖温带半湿润季风区,大陆性季风气候特点显著,温差变化大,四季分明。土壤属砂壤土,土壤pH 7.8,有机质含量1%—1.9%。田间供试作物为春播玉米,播种日期为2017年4月20日。试验区设置不施氮（0%）、中氮（50%）和高氮（100%）3个不同的施氮（纯氮）水平（即0、112.5和225 kg·hm^-2,分别记为N0、N1、N2）。磷钾肥用量100 kg·hm^-2,分别在播种、6月8日、6月20日按4﹕2﹕4分3次施入,各区域用量相等。试验时在每个氮肥区域设置180个小区,共计540个。每个小区长5 m,宽1.2 m,小区内种植两行作物,共计40株,行间距为60 cm,株间距25 cm。不同氮肥区域间设置10行过渡行,周围设置保护行。试验小区的试验地块、灌溉水平、种植密度及田间管理措施相同。试验区地理位置、小区及氮肥水平概况如图1所示。

显示原图|下载原图ZIP|生成PPT
图1研究区地理位置及氮肥水平概况
-->Fig. 1Geographical location of the study area and general situation of nitrogen fertilizer levels
-->

1.2 无人机遥感数据获取与处理

试验时间为7月8日,此时玉米处于开花期。试验以天鹰680型四旋翼无人机为遥感平台,该无人机机身重量约3.6 kg,最大任务载荷2 kg,空载续航时间约为50 min。在无人机上搭载 SONY DSC-QX1数码相机,其有效像素为2 010万,尺寸23.2 mm×15.4 mm,镜头焦距16 mm。无人机遥感数据获取选择太阳光辐射强度稳定、天气晴朗无云时开展,采集时间为12：00—12：30,以降低太阳高度角造成的阴影对影像质量的影响。无人机飞行高度为40 m,航向重叠度设计为80%,旁向重叠度设计为75%,在设定航高下影像空间分辨率为1.06 cm。数据采集时,无人机按照设定好的航线和参数自动巡航并记录数据。
借助Agisoft PhotoScan软件进行无人机高清数码影像的处理工作。将高清数码相片及影像拍摄时刻的POS信息（无人机飞行经纬度、高度、翻转、俯仰及旋转角度）进行匹配;基于动态结构算法检测相片特征点,建立匹配特征点对,进而排列相片;通过密集多视角立体匹配算法生成三维密集点云,为提高精度,利用差分GPS测量的地面控制点信息（图1）进行几何校正,最终生成试验区玉米冠层的正射影像。

1.3 冠层SPAD值测定

在无人机获取遥感数据的当天（7月8日）,采用SPAD-502plus型手持式叶绿素仪测定试验区玉米叶片SPAD值。测量时,在每个小区随机选取完全展开的20片叶子,使用SPAD-502plus型叶绿素仪,在每片叶子的不同部位测定其SPAD,每片叶子测量5次,将其平均值作为该叶片的SPAD值,最后取20张叶片的SPAD值的平均值作为该小区的SPAD值^[25,26]。对获取的540个小区玉米冠层SPAD实测值进行随机抽样,其中28%（n=152）作为建模样本（modeling set）,构建SPAD预测模型;12%（n=68）作为验证样本（validation set）对构建的模型进行验证;60%（n=320）作为测试样本（test set）,对填图后模型的估测精度进行检验。

1.4 研究方法

1.4.1 图像分割及计算冠层覆盖度 RGB数码相机由于成本低、分辨率高、性价比高等优点,在低空遥感平台中得到广泛应用。数码相机所采集的数字图像的RGB的像元值不同于对应波段的反射率,但其本质上是对红、绿、蓝3个波段反射光强的量化表达^[27]。王方永等^[18]研究证实RGB 灰度值同样反映了植被冠层叶片对光的反射特性。冠层覆盖度（canopy cover,CC）是植被像素与小区总像素数的比值,本文利用土壤调整植被指数（soil adjusted vegetation index,SAVI_green）计算CC^[28]。SAVI_green指数将玉米冠层分割为植被像元和非植被像元两个部分,计算方式如下：
$\text{SAV}{{\text{I}}_{\text{green}}}\text{=(1+L) }\!\!\times\!\!\text{ }\frac{\text{(G-R)}}{\text{G+R+L}}$ (1)
式中,G、R表示图像绿色和红色波段的DN值,L代表土壤调节系数,取值范围为0到1,这里L取值为0.5。影像中SAVI_green指数大于零的部分即是玉米冠层像元,其他部分是非植被像元。
1.4.2 植被指数计算将处理好的RGB影像导入到ENVI 5.1软件中进行解译,识别出玉米小区。按照小区大小构建感兴趣区域（region of interest,ROI）,统计ROI内的小区的所有像元的DN值,取其平均值作为该小区的像元值。在此基础上计算两类15种常见的植被指数,包括玉米冠层植被指数（将背景分割后的只包含玉米像元计算的指数,记为VI_plant）和小区植被指数（未分割的小区里所有像元计算的指数,记为VI_plot）,参数及公式出处如表1所示。
Table 1
表1
表1文中所使用的参数及公式
Table 1The parameters and formulas used in the paper

参数Parameters	公式Formula	来源Reference
蓝光标准化值 Normalized blueness intensity, NBI	B/(R+G+B)	KAWASHIMA^[29]
绿光标准化值 Normalized greenness intensity, NGI	G/(R+G+B)	KAWASHIMA^[29]
红光标准化值 Normalized redness intensity, NRI	R/(R+G+B)	KAWASHIMA^[29]
绿红比值指数 Green-red ratio index, GRRI	G/R	GAMON^[30]
红绿比值指数 Red-green ratio index, RGRI	R/G	VERRELST^[31]
蓝绿比值指数 Blue-green ratio index, BGRI	B/G	SELLARO^[32]
蓝红比值指数 Blue-red ratio index, BRRI	B/R	魏全全^[33]
可见光波段差异植被指数visible-band difference vegetation index, VDVI	(2G-R-B)/(2G+R+B)	汪小钦^[34]
植被颜色指数Color index of vegetation, CIVE	0.44R-0.88G+0.39B+18.79	井然^[35]
归一化叶绿素比值植被指数Normalized pigment chlorophyll ratio index, NPCI	(R-B)/(R+B)	PENUELAS^[36]
归一化绿蓝差异指数 Normalized green-blue difference index, NGBDI	(G-B)/(G+B)	HUNT JR^[37]
归一化绿红差异指数 Normalized green-red difference index, NGRDI	(G-R)/(G+R)	GITELSON^[38]
红绿蓝植被指数 Red green blue vegetation index, RGBVI	(G2-R-B)/(G2+R+B)	BENDIG^[39]
超绿指数 Excess green index, EXG	2G-R-B	WOEBBECKE^[40]
差值植被指数Difference vegetation index, DVI	R-B	王方永^[41]

R, G, B are pixel values in red channel, green channel and blue channel respectivelyR、G、B为红、绿、蓝通道的像元值

新窗口打开
1.4.3 数据分析方法本研究利用单变量回归、多元逐步回归和随机森林回归算法构建玉米冠层SPAD值估算模型。其中在单变量模型中,首先通过对VI_plant和VI_plot指数与SPAD的相关性分析,选择相关性较大的指数作为自变量,采用指数、线性、对数、二阶多项式和幂函数构建单变量回归模型。随机森林回归是基于统计学理论的机器学习算法,它利用自助法重抽样技术,通过有放回抽样以及不同树演化过程中随机改变预测变量组合来增加分类树的多样性。每一个分类树可以通过原始数据集（X）中的一个自助法取样子集（Xi）进行生长,并且利用随机选择的m个预测变量中的最佳预测变量进行节点分割。本研究通过调用R语言Random Forests 程序包来建立随机森林模型,分类数的数量（K）和分割节点的随机变量的数量（m）是随机森林模型中两个非常有意义的参数,通过试验不同的回归树数量,根据模型的决定系数和均方根误差来确定K;m不赋值,使用系统默认的输入变量数的1/3,当变量小于3时取1。经过反复试验,最后确定本研究中分类树的数量为1000。
1.4.4 精度评价指标为验证模型的预测精度,将模型预测值与实测值进行回归拟合,选取决定系数（coefficient of determination,R²）、均方根误差（root mean square error,RMSE）和平均相对误差（mean relative error,MRE）进行模型分析检验,计算公式如表2所示。其中决定系数表示预测值与实测值的拟合程度,其值越趋近于1,拟合曲线参考价值越高;均方根误差主要用于模型验证,反映了预测值与实测值的偏离度,其值越小,模型精度越高。
Table 2
表2
表23类模型评价指标
Table 2Three kinds of assessment indices

评价指标 Assessment index	公式 Formula
决定系数 R²	${{R}^{2}}=\frac{\sum\nolimits_{i=1}^{n}{{{({{x}_{i}}-{{{\bar{x}}}_{i}})}^{2}}\times {{({{y}_{i}}-{{{\bar{y}}}_{i}})}^{2}}}}{\sum\nolimits_{i=1}^{n}{{{({{x}_{i}}-\bar{x})}^{2}}\times \sum\nolimits_{i=1}^{n}{{{({{y}_{i}}-\bar{y})}^{2}}}}}$
均方根误差RMSE	$RMSE=\sqrt{\frac{\sum\nolimits_{i=1}^{n}{{{({{y}_{i}}-{{x}_{i}})}^{2}}}}{n}}$
平均相对误差MRE	$MRE=\frac{1}{n}\sum\nolimits_{i=1}^{n}{\left( \frac{\left\| {{x}_{i}}-{{y}_{i}} \right\|}{{{x}_{i}}} \right)\times 100%}$

x_i, $\bar{x}$, y_i, $\bar{y}$were measured value, measured average value, simulated value and simulated average value, n was the measurement timex_i,$\bar{x}$,y_i,$\bar{y}$分别代表实测值、实测值均值、预测值、预测值均值;n为测量次数

新窗口打开

2 结果

2.1 VI_plant和VI_plot指数与玉米SPAD值相关性分析

将各小区测量的玉米冠层SPAD值与VI_plant和VI_plot指数分别进行相关性分析,结果如表3所示。可以看出,VI_plot指数与SPAD之间都存在显著或极其显著关系,其中NGI、VDVI、RGBVI与SPAD值存在显著关系（P<0.05）,其他指数与SPAD值都存在极显著关系（P<0.01）,NRI、DVI、NPCI与SPAD值的相关性绝对值均大于0.77,而BRRI、NBI、NGBDI、BGRI、NGRDI指数与SPAD值相关性绝对值均高于0.7,相关性依次递减;VI_plant指数中除NGI、VDVI指数与SPAD值显著相关外,其他指数皆呈极显著关系,在相关性绝对值大于0.7的指数中,相关性从大到小依次为DVI、NRI、NPCI、BRRI、NBI、NGBDI、BGRI、RGRI、EXG、GRRI,其中,DVI、NRI、NPCI、BRRI与SPAD值的相关性绝对值均大于0.77。综合来看,在VI_plot和VI_plant指数中,BGRI、CIVE、GRRI、NBI、NGRDI、BRRI与SPAD值呈正相关关系,其他指数与SPAD值呈负相关关系。除NGRDI指数外,VI_plant的其他指数与玉米冠层SPAD值的相关性皆高于VI_plot指数。
Table 3
表3
表3VI_plot和VI_plant指数与玉米冠层SPAD相关性分析
Table 3Correlation coefficient for relationships between VI_plot, VI_plant and SPAD

指数Index	R²(VI_plot)	R²(VI_plant)
NGI	-0.1665*	-0.3900*
BGRI	0.7290**	0.7437**
VDVI	-0.1649*	-0.3914*
RGRI	-0.6813**	-0.7280**
CIVE	0.5454**	0.5876**
RGBVI	-0.4908*	-0.5971**
EXG	-0.5896**	-0.7184**
GRRI	0.6957**	0.7085**
NBI	0.7585**	0.7653**
NGBDI	-0.7292**	-0.7444**
NRI	-0.7735**	-0.7758**
NGRDI	0.7093**	0.6756**
DVI	-0.7726**	-0.7765**
BRRI	0.7693**	0.7719**
NPCI	-0.7702**	-0.7739**

**and* indicate significant correlation at 0. 01 and 0. 05 levels, respectively^**和*分别表示0.01和0.05水平上显著相关

新窗口打开
选择与SPAD值相关性皆高于0.76的VI_plot和VI_plant指数,分别统计其在不同的氮肥水平下各指数和CC的平均值,如表4所示。结果表明,随着施氮量的增加,植被CC呈增加趋势;在N0区域,植被VI_plot为0.65时有大量的地表裸露出来,VI_plot指数很大程度上受到背景土壤的影响,与VI_plant间的差异较大;而在施氮水平N1和N2区域,CC增大,无植被覆盖区域面积减少,VI_plot与VI_plant间的差异明显减小。因此,为降低裸露的土壤对模型精度的影响,在下文的研究中我们选用VI_plant指数作为自变量,参与SPAD估测模型的构建。
Table 4
表4
表4不同氮肥区域植被指数和冠层覆盖度的平均值
Table 4Average value of vegetation index and canopy coverage of different nitrogen fertilizer

指数 Index	N0			N1			N2
指数 Index	冠层覆盖度CC	基于小区植被像元计算的指数VI_plant	基于小区所有像元计算的指数VI_plot	冠层覆盖度CC	基于小区植被像元计算的指数VI_plant	基于小区所有像元计算的指数VI_plot	冠层覆盖度CC	基于小区植被像元计算的指数VI_plant	基于小区所有像元计算的指数VI_plot
NRI	0.65	0.3809	0.3847	0.85	0.3432	0.3438	0.91	0.3362	0.3363
NPCI		0.2903	0.2935		0.1369	0.1385		0.1155	0.1156
BRRI		0.5460	0.5523		0.7621	0.7626		0.7972	0.7980
DVI		47.7828	45.8682		21.7613	21.0411		17.8766	17.7022

新窗口打开

2.2 基于VI_plant参数的SPAD值估算

玉米冠层SPAD值与可见光植被指数间有显著的相关性,利用这些指数来对SPAD值进行估算具有较高的可行性。将与SPAD值相关性在0.77以上的NRI、BRRI、NPCI、DVI指数作为自变量,分别使用线性、对数、指数、二次多项式、幂函数5种模型与实测的SPAD值进行拟合构建单变量回归模型,见表5。可以发现,不同波段组合的光谱指数与SPAD值的拟合能力有差异,但各个模型方程均达到极显著水平（P<0.01）,说明参与建立回归模型的各指数均包含可估测的SPAD信息。对于NRI指数,从建模样本来看,决定系数在0.7783和0.7894间,效果最好的是二阶多项式,R²为0.7894;对于BRRI指数,决定系数在0.7819和0.7889间,模型间的拟合精度差距较小,建模效果较好的是幂函数、二阶多项式和对数模型,R²分别为0.7889、0.7863和0.7852,但幂函数的RMSE最大,对数次之,二阶多项式最小;NPCI指数建模效果最好的模型是线性,R²为0.7876,RMSE为4.58;DVI指数决定系数在0.7673和0.7949间,模型间的拟合精度差距较大,效果最好的为线性和二阶多项式,R²分别为0.7866和0.7871,但多项式的RMSE较小。
Table 5
表5
表5玉米冠层SPAD值单变量反演模型
Table 5Single variable inversion models of maize canopy SPAD value

指数 Index	模型 Model	回归方程 Regression equation	训练集Modeling set		验证集 Validation set
指数 Index	模型 Model	回归方程 Regression equation	R²	RMSE	R²	RMSE	MRE (%)
NRI	线性Linear	y = -424.6x + 204.23	0.7815	4.61	0.7891	4.41	6.05
	指数Index	y = 1102.6e^-8.581^x	0.7885	4.75	0.7779	4.58	6.28
	对数Logarithm	y = -152.3ln(x) - 104.52	0.7783	4.65	0.7860	4.45	6.10
	多项式Polynomial	y = -3231.2x² + 1903x - 213.34	0.7894	4.53	0.7976	4.31	5.91
	幂函数Power	y = 2.1539x^-3.077	0.7842	4.81	0.7729	4.64	6.35
BRRI	线性Linear	y = 81.125x - 2.8502	0.7819	4.61	0.7899	4.40	6.17
	指数Index	y = 16.849e^1.6339^x	0.7833	4.69	0.7839	4.51	6.30
	对数Logarithm	y = 53.634ln(x) + 73.796	0.7852	4.57	0.7990	4.31	6.07
	多项式Polynomial	y = -109.62x² + 227.7x - 50.396	0.7863	4.56	0.7930	4.35	6.09
	幂函数Power	y = 78.925x^1.0818	0.7889	4.62	0.7896	4.44	6.17
NPCI	线性Linear	y = -110.75x + 74.382	0.7876	4.58	0.7974	4.20	6.10
	指数Index	y = 79.852e^-2.233^x	0.7877	4.63	0.7877	4.47	6.19
	对数Logarithm	y = -21.22ln(x) + 16.154	0.7684	4.75	0.7777	4.53	6.44
	多项式Polynomial	y = -101.37x² - 68.238x + 70.662	0.7856	4.57	0.7924	4.37	6.03
	幂函数Power	y = 24.757x^-0.426	0.7657	4.90	0.7661	4.71	6.59
DVI	线性Linear	y = -0.6286x + 72.511	0.7866	4.56	0.7956	4.33	5.98
	指数Index	y = 76.986e^-0.013^x	0.7949	4.61	0.7957	4.46	6.20
	对数Logarithm	y = -19.41ln(x) + 117.53	0.7673	4.76	0.7845	4.46	6.20
	多项式Polynomial	y = 0.0018x² - 0.7505x + 74.22	0.7871	4.55	0.7963	4.32	5.95
	幂函数Power	y = 190.26x^-0.391	0.7683	4.99	0.7707	4.67	6.46

新窗口打开
将验证集样本的SPAD实测值和各模型估测值进行拟合分析,结果如表5所示。基于NRI指数建立的模型中,二阶多项式模型的检验精度最优,其R²最大,RMSE最小,平均相对误差MRE最小,其次为线性模型,综合考虑建模精度,二阶多项式模型为NRI指数最佳模型;在BRRI模型中,对数模型的估测精度最佳,R²最大、RMSE、MRE均最小,综合建模结果可知对数模型为BRRI指数最佳估算模型;NPCI模型中,线性模型建模R²最大、RMSE最小、MRE相对较小,综合建模精度,选择线性模型为NPCI指数最佳估算模型;同样,对于DVI指数,无论是建模还是验证时皆是二阶多项式模型效果最佳。综合建模和验证精度,由NRI指数建立的二阶多项式模型效果最好。

2.3 基于随机森林回归模型的SPAD估算

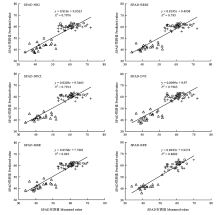
基于机器学习的随机森林模型在光谱分析中应用较为广泛。本文将与玉米冠层SPAD值相关性在0.77以上的VI_plant的NRI、BRRI、NPCI、DVI作为自变量,分别建立单变量回归模型（对每个指数选取最佳的反演模型,分别记为SPAD-NRI、SPAD-BRRI、SPAD-NPCI、SPAD-DVI）、多元回归模型（记为SPAD- MSR）和随机森林回归模型（SPAD-RFR）。6种模型的建模和验证结果如表6、图2和图3所示,结果表明,随机森林回归模型的建模精度和验证精度最高,建模决定系数R²为0.8794,RMSE为3.43,MRE为5.23%,验证集决定系数R²为0.8682,RMSE为3.92,MRE为4.98%;以4种指数联合建立的多元逐步回归模型SPAD-MSR其精度略低于随机森林模型而高于单变量回归模型,R²为0.819,RMSE为4,MRE为5.67%。

显示原图|下载原图ZIP|生成PPT
图2建模样本玉米冠层SPAD 估测值与实测值拟合结果
-->Fig. 2Regression results of estimated and measured maize canopy SPAD values (samples for modeling)
-->

显示原图|下载原图ZIP|生成PPT
图3验证样本玉米冠层SPAD 估测值与实测值拟合结果
-->Fig. 3Regression results of estimated and measured maize canopy SPAD values ( samples for validating)
-->

Table 6
表6
表6不同估算模型的建模、验证与测试结果
Table 6Modeling, validating and testing results under different estimation models

模型 Model	训练集Modeling set			验证集 Validation set			测试集Test set
模型 Model	R²	RMSE	MRE (%)	R²	RMSE	MRE (%)	R²	RMSE	MRE (%)
SPAD-NRI	0.7894	4.53	7.05	0.7976	4.31	5.19	0.7845	4.40	6.09
SPAD-BRRI	0.7852	4.57	7.13	0.7930	4.36	6.07	0.7719	4.51	6.89
SPAD-NPCI	0.7846	4.58	7.14	0.7914	4.38	6.10	0.7704	4.53	6.54
SPAD-DVI	0.7871	4.55	7.05	0.7963	4.32	5.95	0.7769	4.44	6.66
SPAD-MSR	0.7927	4.49	6.19	0.8190	4.00	5.67	0.7921	4.35	5.77
SPAD-RFR	0.8794	3.43	5.23	0.8682	3.92	4.98	0.8247	4.30	5.36

新窗口打开
应用6种模型对试验区可见光影像进行SPAD反演估测,得到试验区玉米冠层SPAD值的分布情况,为了对估算结果的精度进行检验,利用测试集320个小区的SPAD实测值与估算值进行分析（表6）,可以看出,6个模型的检验中,SPAD-RFR模型的估测精度高于多个指数构建的多元逐步回归模型和单变量回归模型,R²为0.8247,RMSE为4.3,MRE为5.36%。图4是将估测效果最佳的随机森林回归模型应用于无人机数码影像,得到试验区玉米冠层SPAD值的分布情况。

显示原图|下载原图ZIP|生成PPT
图4试验区玉米冠层SPAD值分布情况
-->Fig. 4Distribution of SPAD value of maize canopy in the study area
-->

3 讨论

叶绿素是作物吸收光能的主要物质,直接影响了作物的光合作用,SPAD值反映了叶片中叶绿素的总含量,表征作物叶片、冠层的养分和长势情况。研究发现利用土壤调整植被指数分割植被和非植被像元后,计算的VI_plant和VI_plot植被指数与玉米冠层SPAD值的相关性有较大差异。这是因为在低植被覆盖时,植被叶片稀疏,VI_plot易受到土壤像元的影响,而在植被覆盖度较大时,叶片密集,裸露的土壤较少,因此利用分割后的VI_plant指数能够很大程度上降低土壤像元和阴影的影响,使VI_plant指数与SPAD值的相关性大部分高于VI_plot指数,其中NRI、BRRI、NPCI、DVI等指数与SPAD值相关性皆在0.77以上。
研究发现单变量回归模型间的预测精度有细微差异,以NRI指数效果最好,这可能是因为玉米冠层叶绿素相对含量的差异体现在可见光的各个波段上,该指数综合利用了红绿蓝3个波段的信息,一定程度上排除了背景土壤的影响,而其他指数所利用的波段信息有限。除光谱指数外,不同建模方法对估测精度也有较大影响,基于多个植被指数的多元回归模型（SPAD-MSR）预测精度高于单变量回归模型,这可能是因为SPAD-MSR模型利用了相关性高的NRI、BRRI、NPCI、DVI 4种指数,不仅在波段利用方面涵盖了可见光所有波段,而且波段间的不同方式的组合运算使得模型更大程度上利用了各个指数的波段信息,因此具有更好地估测效果。但是从图3中可以看出,它们在无氮区域（N0）出现低估,而在施氮区域（N1、N2）出现了高估现象,这可能是因为不同氮肥区域玉米长势不同。研究中虽然使用了分割后的植被像元计算的植被指数构建SPAD估测模型,但是在无人机获取数据的过程中,无氮区域冠层覆盖度低,冠层反射率依然会受到背景土壤的影响,而施氮区域冠层覆盖度高,植被遮阴严重,从而影响了估测精度。不施氮区域和施氮区域的玉米冠层SPAD值和植被指数之间存在较大的差异,而在施有氮肥的N1和N2区域,虽然施氮量之间有较大差异,但所测得冠层SPAD值和各植被指数之间的差异却不大。而采用随机森林算法的SPAD-RFR模型则很好的缓解了这一现象,它具有很好的抗噪能力也不容易陷入过度拟合,通过对大量分类树的汇总提高了模型的预测精度。
另外,本研究还有一些不足之处。由于本研究重点在于分析利用无人机数码影像提取的光谱指数在估测玉米冠层SPAD的可行性,所以在SPAD值的反演过程中,只讨论了开花期玉米的模型构建,未对其他关键生育期进行研究,因此本文所构建的模型对于其他生育阶段的普适性有待进一步验证。再者,在算法的选择上,本研究仅利用RF算法,并未考虑SPAD遥感估算中常采用的其他算法,如偏最小二乘、支持向量机回归和神经网络等算法。因此,利用不同算法在玉米关键生育期的SPAD反演研究是后续研究的重点。

4 结论

本文利用数码相机对玉米进行了SPAD反演的研究,结果表明利用多旋翼无人机平台搭载数码相机在精确反演农作物叶绿素相对含量方面是可行的,其获取的高空间分辨率RGB影像能够为精准农业提供必要的数据支持。
（1）利用土壤调整植被指数分割植被和非植被像元后,计算的小区范围的植被指数（VI_plot）和只包含作物冠层的植被指数（VI_plant）与玉米冠层SPAD值之间有良好的相关性,VI_plant指数的相关性大部分高于VI_plot指数,其中BRRI、NRI、NPCI、DVI等指数与SPAD相关性在0.77以上。
（2）分别以玉米冠层像元计算的BRRI、NRI、NPCI、DVI指数为自变量建立的单变量回归模型有较高的精度,R²在0.7661—0.799,RMSE在4.2—4.71,其中以NRI指数构建的二次多项式模型效果最好,验证决定系数R²为0.7976,RMSE为4.31。利用相关系数大于0.77的指数构建的多元逐步回归模型（SPAD-MSR）和随机森林回归模型（SPAD-RFR）皆有很高的估测精度,其中SPAD-RFR模型预测效果最好,决定系数R²为0.8682,RMSE为3.92,MRE为4.98%。
（3）应用6种模型对试验区可见光影像进行SPAD
反演估测,SPAD-RFR模型对SPAD的估测值与实测值最为接近,具有较高的反演精度,R²为0.8247,RMSE为4.3,MRE为5.36％,可以作为玉米冠层叶绿素信息监测的主要方法。
（责任编辑杨鑫浩）
The authors have declared that no competing interests exist.